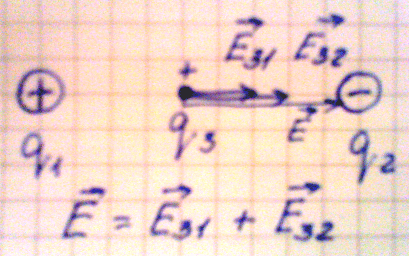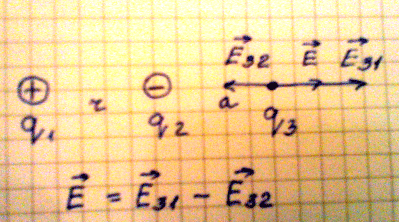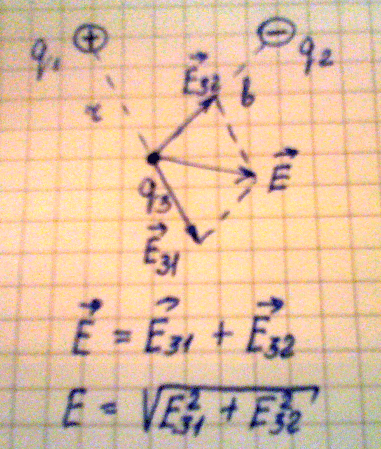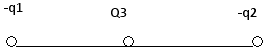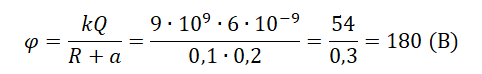Как найти напряженность в точке на расстоянии - Avtoru.top

Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля;
научить учащихся применять формулу E=kq/r² в решении
несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

нигде не пересекаются друг с другом;
имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
между зарядами нигде не прерываются.

Рис.1

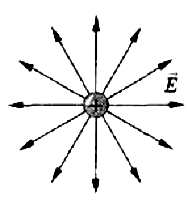
Силовые линии положительного заряда:

Рис.2

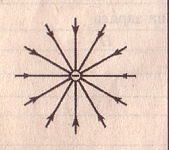
Силовые линии отрицательного заряда:

Рис.3

Силовые линии одноименных взаимодействующих зарядов:

Рис.4

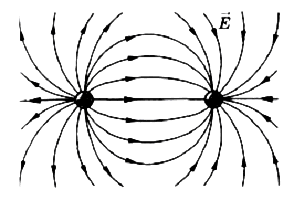
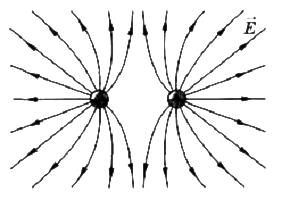
Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

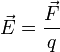
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

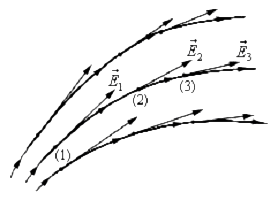
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом:

1. Два заряда q₁ = +3·10^-7 Кл и q₂ = −2·10^-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q₂.

2. В некоторой точке поля на заряд 5·10^-9 Кл действует сила 3·10^-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.

Источник

Условие задачи:

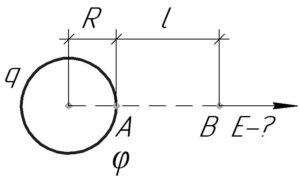
Определить напряженность электрического поля в точке, находящейся на расстоянии 20 см от поверхности заряженной проводящей сферы радиусом 10 см, если потенциал сферы равен 240 В.

Задача №6.3.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(l=20) см, (R=10) см, (varphi=240) В, (E-?)

Решение задачи:

Потенциал сферы (varphi) (т.е. потенциал в точке A – смотрите схему) радиусом (R), несущей некоторый заряд (q), можно определить так:

[varphi = frac{{kq}}{R};;;;(1)]

Модуль напряженности электрического поля (E), создаваемого заряженной сферой с зарядом (q) и радиусом (R), на расстоянии (l) от поверхности сферы (в точке B – смотрите схему) легко найти по формуле:

[E = frac{{kq}}{{{{left( {R + l} right)}^2}}};;;;(2)]

Поделим (2) на (1), тогда:

[frac{E}{varphi } = frac{R}{{{{left( {R + l} right)}^2}}}]

В итоге получим:

[E = frac{{varphi R}}{{{{left( {R + l} right)}^2}}}]

Численно напряженность электрического поля (E) равна:

[E = frac{{240 cdot 0,1}}{{{{left( {0,1 + 0,2} right)}^2}}} = 266,7;В/м approx 2,67;В/см]

Ответ: 2,67 В/см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.3 При сообщении металлической сфере радиусом 10 см некоторого заряда
6.3.5 На расстоянии 10 м от центра заряженного металлического шара радиусом 3 м
6.3.6 Определить потенциал шара радиусом 10 см, находящегося в вакууме

Источник

Электрическое поле. Напряженность электрического поля. Линии напряженности электрического поля (силовые линии). Однородное электрическое поле. Напряженность электростатического поля точечного заряда. Принцип суперпозиции полей. Теорема Гаусса. Электростатическое поле равномерно заряженных плоскости, сферы и шара.

Электрическое поле представляет собой векторное поле, существующее вокруг тел или частиц, обладающее электрическим зарядом, а также возникающее при изменении магнитного поля.

Напряженность электрического поля — это отношение вектора силы (vec{F}), с которой поле действует на пробный заряд (q), к самому пробному заряду с учетом его знака.

[vec{E}=dfrac{vec{F}}{q}]

Единицы измерения: (displaystyle [text{В}/text{м}]) (вольт на метр).

всегда начинаются на положительных зарядах и заканчиваются на отрицательных.

— такое поле в данной области пространства. если вектор напряженности поля одинаков в каждой точке области.

При равномерном распределении электрического заряда (q) по поверхности площади (S) поверхностная плотность заряда (displaystyle sigma) постоянна и равна

[sigma =dfrac{q}{S}]

Напряженность электростатического поля точечного заряда Q в точке A, удаленной на расстояние (r) от заряда (Q), определяется формулой:

[E=dfrac{kcdot |Q|}{r^2}]

Принцип суперпозиции полей

Пусть заряды (displaystyle q_1, q_2, q_3,… , q_n) по отдельности создают в данной точке поля (vec{E}_1), (vec{E}_2),…,(vec{E}_n). Тогда система этих зарядов создает в данной точке поле (vec{E}), равное векторной сумме напряженностей полей отдельных зарядов.

[vec{E}=vec{E}_1+vec{E}_2+…+vec{E}_n]

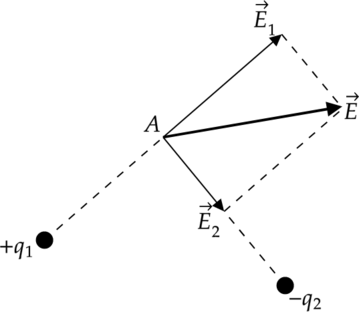
Разберемся, что такое принцип суперпозиции на примере электрического поля. Благодаря ему, можно найти напряженность двух точечных зарядов, в каждой точке поля (А). Рассмотрим рисунок:

здесь видно, что для нахождения направления результирующего вектора (vec{E}), нужно сложить вектора (vec{E}_1) и (vec{E}_2) по правилу параллелограмма. Это и есть принцип суперпозиции.

Теорема Гаусса

Поток вектора напряженности электростатического поля (vec{E}) через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную (varepsilon_0).

Заряженная плоскость

Её электрическое поле однородно, то есть его напряжённость одинакова на любом расстоянии от плоскости, линии напряжённости параллельны. По теореме Гаусса:

[E=dfrac{|sigma|}{2varepsilon_0varepsilon}]

Заряженная сфера

Рассмотрим электрическое поле равномерно заряженной сферы. Поток напряжённости через любую замкнутую поверхность внутри сферы равен нуля, так как внутри этой поверхности нет заряда. Отсюда следует, что внутри сферы напряжённость равна нулю.

(E=0) при (r<R).

Проведём сферическую поверхность радиусом (r>R). Пусть её заряд равен (q). По теореме Гаусса:

[E=kdfrac{|q|}{r^2varepsilon}]

Заряженный шар

Рассмотрим электрическое поле равномерно заряженного шара. Напомним, что объём шара равен (V=dfrac{4}{3}pi R^3). Тогда его заряд (q=dfrac{4}{3}pi R^3rho). Напряжённость поля вне шара (r>R) можно найти так же, как и вне сферы:

[E=kdfrac{4pi R^3 rho}{3r^2varepsilon}]

Для нахождения напряжённости внутри шара применим теорему Гаусса для сферической поверхности радиусом (r<R). По теореме Гаусса:

[E=kdfrac{4pi rho r}{3varepsilon}]

Источник

Законом Кулона описывается взаимодействие заряженных частиц. Однако большинство сил, с которыми мы работали, возникает при взаимодействии тел посредством контакта (т.е. тела касаются друг друга). В случае электромагнитного взаимодействия контакта нет, тогда взаимодействие происходит посредством неких невидимых элементов. Тогда взаимодействия между частицами вещества и удалёнными друг от друга макроскопическими телами осуществляются через посредство физических полей, которые создаются этими частицами или телами в окружающем пространстве. В случае с заряженными частицами, эти поля назовём электромагнитными.

Тогда логика электромагнитного взаимодействия такова: заряд создаёт вокруг себя электромагнитное поле, которое, в свою очередь, действует на любой другой заряд displaystyle q , находящийся на любом расстоянии от источника.

Закон Кулона описывает взаимодействие между двумя зарядами:

$displaystyle left| {{F}_{k}} right|=kfrac{left| Q right|left| q right|}{{{r}^{2}}}$ (1)

где

Рис. 1. Закон Кулона. Пробный заряд

Сила (1) зависит от обоих зарядов, что не позволяет толком описать электрическое поле, создаваемое каждым из взаимодействующих частиц. Тогда придумаем немного другую систему: возьмём пробный заряд — некий малый заряд, который не будет искажать поле исследуемого нами заряда displaystyle left| Q right| . Поместим пробный заряд в различные точки пространства рядом с исследуемым нами зарядом и проиллюстрируем силы Кулона (рис. 1).

В принципе, значение силы Кулона можно найти в любой точке пространства, однако данные силы зависят как от заряда источника, так и от значения пробного заряда. Введём новую переменную, поделив значение силы Кулона на значение пробного заряда:

$displaystyle vec{E}=frac{{{{vec{F}}}_{k}}}{q}$ (2)

где
- — вектор напряжённости электрического поля.

Подставим силу Кулона в (1):

$displaystyle vec{E}=kfrac{Qq}{q{{r}^{3}}}vec{r}=kfrac{Q}{{{r}^{3}}}vec{r}$ (3)

Исходя из (3), можно заключить, что напряжённость электрического поля зависит от заряда источника поля и точки наблюдения, описываемой расстоянием от заряда (рис. 2).

Рис. 2. Напряжённость электрического поля

Т.е. напряжённость электрического поля — параметр, описывающий поле, создаваемое зарядом-источником. Значение напряжённости электрического поля позволяет оценить сильно или слабо будет действовать поле на заряд, помещённый в него. Размерность displaystyle vec{E} — В/м.

Исходя из (3), можно найти напряжённость поля точечного заряда. Напряжённость электрического поля — величина векторная, поэтому для её нахождения необходимо знать как модуль, так и направление вектора. Начнём с модуля:

$displaystyle left| {vec{E}} right|=kfrac{left| Q right|}{{{r}^{3}}}left| {vec{r}} right|=kfrac{left| Q right|}{{{r}^{2}}}$ (4)

Рис. 3. Напряжённость электрического поля (направление)

Чтобы выяснить направление вектора, воспользуемся уравнением (2). Исходя из (2), можно заключить, что направление напряжённости электрического поля совпадает с направлением силы Кулона, а направление силы Кулона зависит от знака взаимодействующих зарядов. Чтобы не заморачиваться с рассмотрением этих зарядов в каждой задаче, просто договоримся. Если источник поля (заряд) положителен, тогда напряжённость поля направлена от заряда, если источник поля (заряд) отрицателен, тогда напряжённость поля направлена к заряду (рис. 3).

Напряжённость системы зарядов. Принцип суперпозиции напряжённости.

В случае, если в задаче источниками поля являются несколько зарядов, тогда напряжённость в интересующей точке можно найти как векторную сумму напряжённостей от каждого из зарядов:

$displaystyle {{vec{E}}_{o}}=sumlimits_{i}{{{{vec{E}}}_{i}}}$ (5)

где

Важно: поиск векторной суммы чаще всего сопряжён с реализацией теоремы Пифагора, теоремы косинусов или синусов, иногда с проецированиием векторов напряжённости на оси с последующим суммированием.

Рис. 4. Принцип суперпозиции напряжённости

Проиллюстрируем: пусть в системе присутствует 3 заряда ( $displaystyle {{q}_{2}}$ , $displaystyle {{q}_{3}}$ , $displaystyle {{vec{r}}_{1}}$ ), найти напряжённость в точке А, находящейся на заданном расстоянии от каждого из них ( $displaystyle {{vec{r}}_{2}}$ , $displaystyle {{vec{r}}_{3}}$ , $displaystyle {{vec{r}}_{3}}$ ) (рис. 4).

Пользуясь знаниями о зарядах, расставляем направления напряжённостей от каждого из зарядов, значение модуля каждой из них можем найти из (4). А далее геометрически складываем, получая искомый $displaystyle {{vec{E}}_{o}}$ .

Напряжённость поля бесконечной заряженной плоскости.

Отдельно в школьной физике рассматривается бесконечная (осень большая) заряженная равномерно плоскость (рис. 5).

Рис. 5. Напряжённость бесконечной плоскости

Напряжённость такой плоскости вблизи её:

$displaystyle E=frac{sigma }{2varepsilon {{varepsilon }_{0}}}$ (6)

где

В (6) использовалось определение поверхностной плотности заряда:

$displaystyle sigma =frac{Q}{S}$ (7)

где

Важно: напряжённость бесконечной плоскости не зависит от расстояния от плоскости.

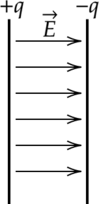
Напряжённость поля двух бесконечных заряженных плоскостей (конденсатор).

Рис. 6. Напряжённость двух бесконечных плоскостей

Если составить систему из двух бесконечных плоскостей, заряженных одинаковым по модулю и различным по знаку зарядом (при этом площади плоскостей одинаковы), то общая напряжённость между ними:

$displaystyle {{E}_{0}}=frac{sigma }{2varepsilon {{varepsilon }_{0}}}+frac{sigma }{2varepsilon {{varepsilon }_{0}}}=frac{sigma }{varepsilon {{varepsilon }_{0}}}=frac{q}{varepsilon {{varepsilon }_{0}}S}$ (8)

Уравнение (8) характеризует напряжённость внутри конденсатора (рис. 6).

Вывод: в случае, если в задаче требуется найти напряжённость, она дана, достаточно рассмотреть систему. Различных систем, а соответственно, и формул, немного: точечный заряд, шар, система точечных зарядов и бесконечные плоскости. Для каждой системы — своё решение.

Источник

Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.

Электростатическое поле точечного заряда

Направление силовых линий электростатического поля точечного заряда

Модуль напряженности не зависит от значения пробного заряда q₀:

E=FKq0=kQq0r2q0=kQr2

Модуль напряженности точечного заряда в вакууме:

E=kQr2

Модуль напряженности точечного заряда в среде:

E=kQεr2

Сила Кулона:

−FKулона=q−E

Потенциал не зависит от значения пробного заряда q₀:

φ=Wpqo=±kQq0rq0=±kQr

Потенциал точечного заряда в вакууме:

φ=±kQr

Потенциал точечного заряда в среде:

φ=±kQεr

Внимание! Знак потенциала зависит только от знака заряда, создающего поле.

Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.

Работа электрического поля по перемещению точечного заряда:

A12=±q(φ1−φ2)

Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз?

Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:

E=kQεr2

Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.

Электростатическое поле заряженной сферы

Направление силовых линий электростатического поля заряженной сферы:

Модуль напряженности электростатического поля заряженной сферы:

Внутри проводника (расстояние меньше радиуса сферы, или r < R)

E=0

На поверхности проводника (расстояние равно радиусу сферы, или r = R)

E=kQR2

Вне проводника (расстояние больше радиуса сферы, или r > R)

E=kQr2=kQ(R+a)2

a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки.

Сила Кулона:

−FK=q−E

Потенциал:

Внутри проводника и на его поверхности (r < R или r = R)	φ=±kQR
Вне проводника (r > R)	φ=±kQr=±φ=±kQR+a

Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.

6 нКл = 6∙10^–9 Кл

Так как сфера заряжена положительно, то потенциал тоже положителен:

Задание EF18107

Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?

Ответ:

а) F

б) nF

в) Fn

г) n²F

Алгоритм решения

1.Записать исходные данные.

3.Применить закон Кулона к обоим зарядам для 1 и 2 случая.

4.Установить, как меняется сила, с которой заряды действуют друг на друга.

Решение

Запишем исходные данные:

• Первая пара зарядов: q₁ и q₂.

• Вторая пара зарядов: q₁’ = nq₁ и q₂’=q₂/n.

• Расстояние между зарядами: r₁ = r₂ = r.

Закон Кулона:

FK=k|q1||q2|r2

Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:

FK1=k|q1||q2|r2

Закон Кулона для второй пары:

FK2=k|nq1|∣∣q2n∣∣r2=k|q1||q2|r2

Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:

FK1=FK2

После изменения зарядов модуль силы взаимодействия между ними останется равным F.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18591

В трёх вершинах квадрата размещены точечные заряды: +q, –q, +q (q >0) (см. рисунок). Куда направлена кулоновская сила, действующая со стороны этих зарядов на точечный заряд +2q, находящийся в центре квадрата?

Ответ:

а) ↘

б) →

в) ↖

г) ↓

Алгоритм решения

1.Сделать чертеж. Обозначить все силы, действующие на центральный точечный заряд со стороны остальных точечных зарядов.

2.Найти равнодействующую сил геометрическим способом.

Решение

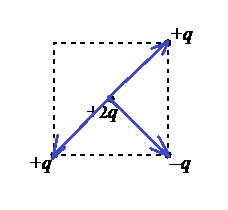
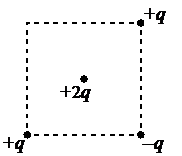
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:

Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.

Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22574

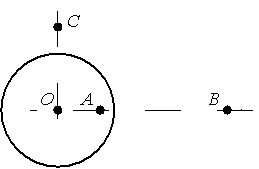
На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?

Установите соответствие между физическими величинами и их значениями.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать формулы для нахождения напряженности электростатического поля внутри и снаружи заряженной сферы.

2.Определить величину напряженности поля в указанных точках.

3.Установить соответствие между величинами и их значениями.

Решение

Внутри заряженной сферы напряженность электростатического поля равна 0. Поэтому напряженность в точке А равна 0.

EA=0

Снаружи заряженной сферы напряженность электростатического поля равна:

E=kQr2=kQ(R+a)2

Найдем напряженность электростатического поля в точке В, которая находится на расстоянии 3R от центра заряженной сферы:

EB=kQr2=kQ(3R)2=kQ9R2

Чтобы выразить EB через Eс, найдем напряженность электростатического поля в точке С, которая находится на расстоянии 3R/2 от центра заряженной сферы:

EС=kQr2=kQ(32R)2=4kQ9R2

Найдем отношение EB к Eс:

EBEС=kQ9R2÷4kQ9R2=kQ9R2·9R24kQ=14

Следовательно:

EB=EС4

Ответ: 14

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 7.5k

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 2,67 В/см.

Смотрите также задачи:

Электростатическое поле точечного заряда

Направление силовых линий электростатического поля точечного заряда

Электростатическое поле заряженной сферы

Не пропустите также: