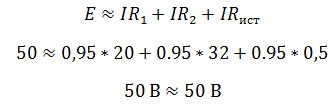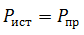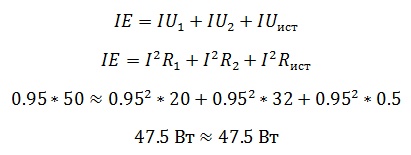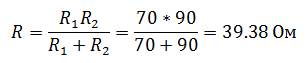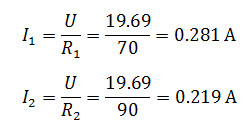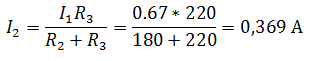Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
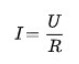
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
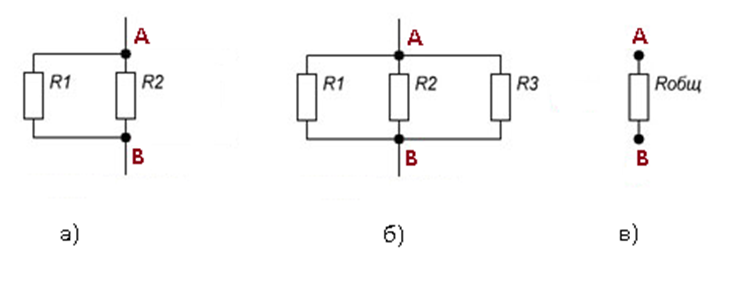
Общие схемы типов соединений представлены на рисунке 1.
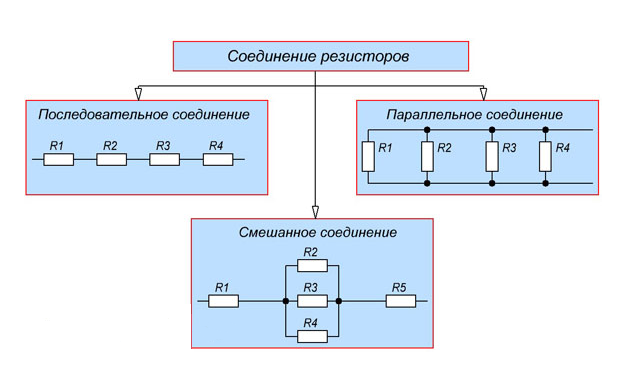
Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
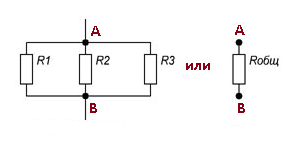
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
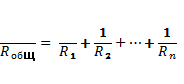
и рассчитывается по формуле:
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
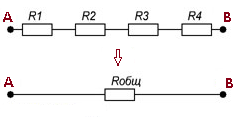
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
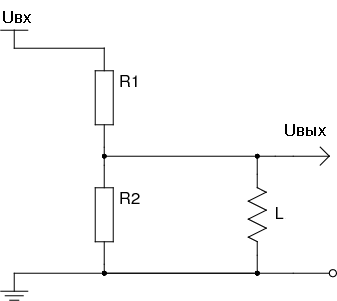
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
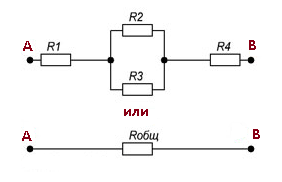
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
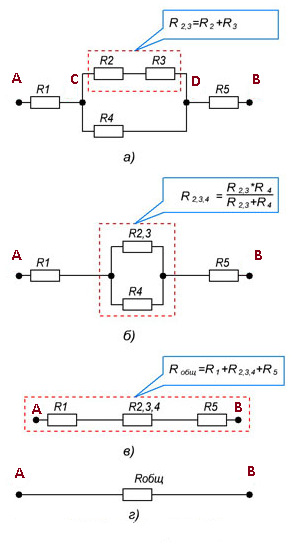
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Загрузить PDF
Загрузить PDF
В параллельной цепи резисторы соединены таким образом, что электрический ток в цепи делится между резисторами и проходит через них одновременно (сравните это с автодорогой, которая разделяется на две параллельные дороги и делит поток машин на два потока, движущихся параллельно друг другу). В этой статье мы расскажет вам, как вычислить напряжение, силу тока и сопротивление в параллельной цепи.
Шпаргалка
- Формула для вычисления общего сопротивления RT в параллельной цепи: 1/RT = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение в параллельной цепи одинаковое на каждом ее элементе: VT = V1 = V2 = V3 = …
- Формула для вычисления общей силы тока в параллельной цепи: IT = I1 + I2 + I3 + …
- Закон Ома: V = IR
-
1
Определение. Параллельная цепь — это цепь, в которой ток течет из точки А в точку В одновременно по нескольким элементам цепи (то есть поток электронов разбивается на несколько потоков, которые на конечном участке цепи вновь объединяются в единый поток). В большинстве задач, в которых присутствует параллельная цепь, нужно вычислить напряжение, сопротивление и силу тока.
- Элементы, подключенные параллельно, находятся на отдельных ветвях цепи.
-
2
Сила тока и сопротивление в параллельных цепях. Представьте себе автостраду с несколькими полосами, на каждой из которых установлен пункт пропуска, замедляющий движение автомобилей. Построив новую полосу, вы увеличите скорость движения (даже если и на этой полосе вы поставите пункт пропуска). Аналогично с параллельной цепью — добавив новую ветвь, вы уменьшите общее сопротивление цепи и увеличите силу тока.
-
3
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + …
-
4
Общее сопротивление в параллельной цепи. Оно вычисляется по формуле: 1/RT = 1/R1 + 1/R2 + 1/R3 + …, где R1, R2 и так далее — это сопротивление соответствующих элементов (резисторов) этой цепи.
- Например, параллельная цепь включает два резистора и сопротивление каждого равно 4 Ом. 1/RT = 1/4 + 1/4 → 1/RT = 1/2 → RT = 2 Ом. То есть общее сопротивление параллельной цепи с двумя элементами, сопротивления которых равны, в два раза меньше сопротивления каждого резистора.
- Если какая-либо ветвь параллельной цепи не имеет сопротивления (0 Ом), то весь ток пройдет именно через эту ветвь.[1]
-
5
Напряжение. Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Так как здесь рассматриваются две точки без учета пути движения тока по цепи, напряжение в параллельной цепи одинаково на каждом элементе этой цепи, то есть: VT = V1 = V2 = V3 = …
-
6
Вычислите значения неизвестных величин по закону Ома. Закон Ома описывает взаимосвязь между напряжением V, силой током I и сопротивлением R: V = IR. Если вам известны значения двух величин из этой формулы, вы можете найти значение третьей величины.
- Вы можете применить закон Ома для всей цепи (V = ITRT) или для одной ветви этой цепи (V = I1R1).
Реклама
-
1
Нарисуйте таблицу, чтобы облегчить решение задачи, особенно если неизвестны значения сразу нескольких величин в данной параллельной цепи.[2]
Рассмотрим пример электрической цепи с тремя параллельными ветвями. Обратите внимание, что здесь под ветвями подразумеваются резисторы с сопротивлениями R1, R2, R3.R1 R2 R3 Общее Единицы измерения V В I А R Ом -
2
Внесите в таблицу данные вам значения. Например, к электрической цепи подключена батарея, напряжение которой равно 12 В. Цепь включает три параллельные ветви с сопротивлениями 2 Ом, 4 Ом, 9 Ом.
R1 R2 R3 Общее Единицы измерения V 12 В I А R 2 4 9 Ом -
3
Заполните значения напряжения для каждого элемента цепи. Помните, что общее напряжение в параллельной цепи и напряжение на каждом резисторе этой цепи равны.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I А R 2 4 9 Ом -
4
Вычислите силу тока на каждом резисторе по закону Ома. Так как теперь в каждом столбце вашей таблицы есть значения двух величин, вы с легкостью вычислите значение третей величины при помощи закона Ома: V = IR. В нашем примере нужно найти силу тока, поэтому перепишите формулу закона Ома следующим образом: I = V/R
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 12/2 = 6 12/4 = 3 12/9 = ~1,33 А R 2 4 9 Ом -
5
Вычислите общую силу тока. Помните, что общая сила тока в параллельной цепи равна сумме сил тока на каждом элементе этой цепи.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1,33 6 + 3 + 1,33 = 10,33 А R 2 4 9 Ом -
6
Вычислите общее сопротивление. Сделайте это одним из двух способов. Либо используйте формулу
1/RT = 1/R1 + 1/R2 + 1/R3, либо формулу закона Ома: R = V/I.R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1.33 10,33 А R 2 4 9 12 / 10,33 = ~1,17 Ом Реклама
-
1
Вычислите мощность тока по формуле: P = IV. Если вам дана мощность тока на каждом участке цепи, то общая мощность вычисляется по формуле: PT = P1 + P2 + P3 + ….
-
2
Вычислите общее сопротивление в параллельной цепи, состоящей из двух ветвей (двух резисторов).
- RT = R1R2 / (R1 + R2)
-
3
Найдите общее сопротивление в параллельной цепи, если сопротивление всех резисторов одинаково: RT = R1 / N, где N — количество резисторов в цепи.[3]
- Например, если в параллельной цепи два резистора с одинаковым сопротивлением, то общее сопротивление цепи будет вдвое меньше сопротивления одного резистора. Если в цепи восемь одинаковых резисторов, то общее сопротивление будет в восемь раз меньше сопротивления одного резистора.
-
4
Вычислите силу тока на каждом резисторе, если напряжение неизвестно. Это можно сделать, воспользовавшись правилом Кирхгофа.[4]
Вам необходимо вычислить сопротивление каждого резистора и общую силу тока в цепи.- Два резистора в параллельной цепи: I1 = ITR2 / (R1 + R2)
- Несколько (более двух) резисторов в параллельной цепи. В этом случае для вычисления I1 найдите общее сопротивление всех резисторов за исключением R1. Для этого воспользуйтесь формулой для вычисления общего сопротивления в параллельной цепи. Затем используйте правило Кирхгофа, заменив R2 полученным значением.
Реклама
Советы
- В параллельной цепи напряжение одинаково на всех резисторах.
- Возможно, в вашем учебнике закон Ома представлен следующей формулой: E = IR или V = AR. Здесь присутствуют другие обозначения величин, но суть закона Ома не меняется.
- Общее сопротивление часто именуется эквивалентным сопротивлением.
- Если у вас нет калькулятора, найти общее сопротивление, используя значения R1, R2 и так далее, довольно проблематично. Поэтому воспользуйтесь законом Ома.
- Если в задаче дана параллельно-последовательная цепь, сделайте вычисления для ее параллельного участка, а затем для полученной последовательной цепи.
Реклама
Об этой статье
Эту страницу просматривали 173 049 раз.
Была ли эта статья полезной?
Download Article
Download Article
Before you can calculate the voltage across a resistor, you’ll first have to determine what kind of circuit you are using. If you need a review of the basic terms or a little help understanding circuits, start with the first section. Otherwise, jump ahead to the type of circuit you have to solve.
-
1
Learn about current. Let’s think about current by using an analogy: imagine you pour a bag of corn kernels into a bowl. Each corn kernel is an electron, and the stream of kernels flowing into the bowl is the current.[1]
When talking about the flow, you describe it by saying how many kernels are flowing each second. When talking about a current, you measure it in amperes (amps), or a certain (very large) number of electrons flowing per second. -
2
Think about electrical charge. Electrons have a «negative» electrical charge. This means they attract (or flow toward) objects with a positive charge, and repel (or flow away from) objects with a negative charge. Since they’re all negative, electrons are always trying to push away from other electrons, spreading out wherever they can.
Advertisement
-
3
Understand voltage. Voltage measures the difference in electrical charge between two points. The greater the difference, the more energetically the two sides attract each other. Here’s an example with an everyday battery:
- Inside a battery, chemical reactions happen that produces a buildup of electrons. The electrons go to the negative end, while the positive end stays mostly empty. (These are called the negative and positive terminals.) The longer this goes on, the larger the voltage between the two ends.
- When you connect a wire between the negative and positive ends, the electrons at the negative end suddenly have somewhere to go. They shoot toward the positive end, creating a current. The larger the voltage, the more electrons move to the positive end each second.
-
4
Figure out resistance. Resistance is exactly what it sounds like. The more resistance something has, the harder it is for the electrons to push through. This slows the current, since fewer electrons can push through each second.
- A resistor is anything in the circuit that adds resistance. You can buy an actual «resistor» at an electronics store, but in a circuits problem it might represent a light bulb or anything else with resistance.
-
5
Memorize Ohm’s Law. There’s a very simple relationship between current, voltage, and resistance.[2]
Write this down or memorize it; you’ll use it often when solving circuit problems:- Current = voltage divided by resistance
- This is usually written: I = V / R
- Think about what happens when you increase V (voltage) or R (resistance). Does this match what you learned in the explanations above?
Advertisement
-
1
Understand a series circuit. A series circuit is easy to identify. It’s just one loop of wire, with everything arranged in a row. The current flows around the entire loop, going through each resistor or element in order.
- The current is always the same at any point along the circuit.[3]
- When calculating voltage, it doesn’t matter where the resistor is on the circuit. You can pick up the resistors and move them around, and you’ll still have the same voltage across each one.
- We’ll use an example circuit with three resistors in series: R1, R2, and R3. This is powered by a 12 volt battery. We’ll find the voltage across each one.
- The current is always the same at any point along the circuit.[3]
-
2
Calculate the total resistance. Add together all resistance values on the circuit. The answer is the total resistance of the series circuit.
- For example, the three resistors R1, R2, and R3 have resistances of 2 Ω (ohms), 3 Ω, and 5 Ω respectively. The total resistance is 2 + 3 + 5 = 10 ohms.
-
3
Find the current. Use Ohm’s Law to find the current of the entire circuit. Remember, the current is the same anywhere on a series circuit. Once we calculate the current this way, we can use it for all our calculations.
- Ohm’s Law says that the current I = V / R. The voltage across the whole circuit is 12 volts, and the total resistance is 10 ohms. The answer is I = 12 / 10 = 1.2 amperes.
-
4
Adjust Ohm’s Law to solve for voltage. With basic algebra, we can change Ohm’s Law to solve for voltage instead of current:[4]
- I = V / R
- IR = VR / R
- IR = V
- V = IR
-
5
Calculate the voltage across each resistor. We know the resistance, we know the current, and we have our equation. Plug in the numbers and solve. Here’s our example problem solved for all three resistors:
- Voltage across R1 = V1 = (1.2A)(2Ω) = 2.4 volts.
- Voltage across R2 = V2 = (1.2A)(3Ω) = 3.6 volts.
- Voltage across R3 = V3 = (1.2A)(5Ω) = 6.0 volts.
-
6
Check your answer. In a series circuit, the sum of all your answers must equal the total voltage.[5]
Add up every voltage you calculated and see if you get the voltage of the entire circuit. If you didn’t, go back and check for mistakes.- In our example, 2.4 + 3.6 + 6.0 = 12 volts, the voltage across the whole circuit.
- If your answer is slightly off (for instance, 11.97 instead of 12), you probably rounded a number at some point. Your answer is still correct.
- Remember, voltage measures the differences in charge, or numbers of electrons. Imagine counting the number of new electrons you see as you travel along the circuit. If you count them correctly, you’re going to end up with the total change in electrons from the beginning to the end.
Advertisement
-
1
Understand parallel circuits. Imagine a wire leaving one end of a battery, then splitting into two separate wires. These two wires run parallel to each other, then join up again before they reach the other end of the battery. If there’s a resistor on the left wire and a resistor on the right wire, those two resistors are connected «in parallel.»[6]
- You can have any number of wires in a parallel circuit. These instructions will still work for a circuit that splits into one hundred wires and comes back together.
-
2
Think about how the current flows. In a parallel circuit, the current flows across each path available to it. Current will flow through the wire on the left, cross the left resistor, and reach the other end. At the same time, current will flow through the wire on the right, cross the right resistor, and reach the end. No part of the current doubles back or flows through two parallel resistors.
-
3
Use the total voltage to find the voltage across each resistor. If you know the voltage across the whole circuit, the answer is surprisingly easy. Each parallel wire has the same voltage as the entire circuit.[7]
Let’s say a circuit with two parallel resistors is powered by a 6 volt battery. The voltage across the left resistor is 6 volts, and the voltage across the right resistor is 6 volts. It doesn’t even matter how much resistance there is. To understand why, think back to the series circuits described above:- Remember that adding voltage drops in a series circuit always results in the total voltage across the circuit.
- Think of each path the current takes as a series circuit. The same holds true for this: if you count up all the voltage drops, you’ll end up with the total voltage.
- Since the current through each of the two wires only passes through one resistor, the voltage across that resistor must equal the total voltage.
-
4
Calculate the total current of the circuit. If the problem doesn’t tell you what the total voltage of the circuit is, you’ll need to complete a few more steps. Start by finding the total current passing through the circuit. In a parallel circuit, the total current is equal to the sum of the current running through each parallel path.[9]
- In mathematical terms: Itotal = I1 + I2 + I3…
- If you’re having trouble understanding this, imagine a water pipe split into two paths. The total amount of water flow is just the amount of water flow in each pipe, added together.
-
5
Compute the total resistance of the circuit. Resistors are not as effective in a parallel circuit, because they only block the current going along one wire. In fact, the more wires there are, the easier it is for the current to find a way through. To find the total resistance, solve for Rtotal in this equation:[9]
- 1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 …
- For example, a circuit has a 2 ohm and a 4 ohm resistor in parallel. 1 / Rtotal = 1/2 + 1/4 = 3/4 → 1 = (3/4)Rtotal → Rtotal = 1/(3/4) = 4/3 = ~1.33 ohms.
-
6
Find the voltage from your answers. Remember, once we find the total voltage of the circuit, we have found the voltage across any one of the parallel wires. Solve for the whole circuit using Ohm’s law.[10]
Here’s an example:- A circuit has 5 amperes of current running through it. The total resistance is 1.33 ohms.
- According to Ohm’s Law, I = V / R, therefore V = IR
- V = (5A)(1.33Ω) = 6.65 volts.
Advertisement
Add New Question
-
Question
What is the percentage of applied voltage that will be dropped across r3=70 if r1=80 and r2=50?
It would be 35%. The higher the resistance, the higher the voltage drop. The ratio of resistances here is 80:50:70. Solving for 70 ohms, we get 35%.
-
Question
What is the voltage of a 60 ohm resistor if the circuit voltage is 150 volts with two parallel 30 ohm resistors and one 60 ohm resister in the series?
Assuming you intend to ask what is the voltage drop across the 60 ohm resistor, the answer is 120v. The two parallel 30 ohm resistors have an equivalent resistance of 15 ohms. 1/(1/30 + 1/30) = 15. The total resistance appears as 75 ohms to the 150v source. Find the circuit current by I = E/R or I = 150/75 = 2 amps. Find the voltage drop for the 60 ohm resistor with E = I x R or E = 2 x 60 = 120V drop across the 60 Ohm resistor.
-
Question
What becomes the Voltage if we use 2 resistors of 4W in parallel?
As any other data is not provided, the voltage across two resistors of 4w in parallel is the same.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you have a complicated circuit that involves resistors in series and resistors in parallel, pick two nearby resistors. Find the total resistance across them using the rules for resistors in parallel or in series, as appropriate. Now you can treat them as a single resistor. Keep doing this until you have a simple circuit with resistors either in parallel or in series.[11]
-
The voltage across a resistor is often called a «voltage drop.»
-
Understand the terminology:
- Circuit – composed of elements (e.g. resistors, capacitors, and inductors) connected by wires and wherein current can pass through
- Resistors – elements that can reduce or resist current
- Current – flow of charge into wires; unit: Ampere, A
- Voltage – work done per unit charge; unit: Voltage, V
- Resistance – measurement of the opposition of an element to electric current; unit: Ohm, Ω
Advertisement
References
About This Article
Article SummaryX
To calculate voltage across a resistor in a series circuit, start by adding together all of the resistance values in the circuit. Then, divide the voltage across the circuit by the total resistance to find the current. Once you have the current, calculate voltage for the individual resistors by multiplying the current by the resistance. For example, in a series circuit with 3 resistors of 2, 3 and 5 Ohms, and a voltage of 12 volts, the current would be 12 divided by 10, or 1.2 amperes. For the 2 Ohm resistor, the voltage would be 1.2 times 2, or 2.4 volts. If you want to learn how to calculate voltage in a parallel circuit, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 916,089 times.
Reader Success Stories
-
Mohd Rodzi Mohamad
Aug 26, 2016
«This article is very neatly and clearly explained with illustrations of pictures for better comprehension. Very…» more
Did this article help you?
Соединения проводников
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.
Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):
Рис. 1. Резистор
Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки
в точку
, проходя через резистор
(рис. 2):
Рис. 2.
Стационарное поле совершает при этом положительную работу .
Так как и
, то и
, т. е.
.
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и
, то
. (рис. 3):
Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и
, соединённых последовательно и подключённых к источнику постоянного напряжения
(рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.
Действительно, напряжение на участке
— это работа поля по переносу единичного заряда из точки
в точку
; напряжение
на участке
— это работа поля по переносу единичного заряда из точки
в точку
. Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки
в точку
, то есть напряжение
на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть — сопротивление участка
. По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами
и
.
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и
. Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от
к
(по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и
на резисторах
и
равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время
из неразветвлённого участка поступает заряд
. За это же время
из точки
к резистору
уходит заряд
, а к резистору
— заряд
.
Ясно, что . В противном случае в точке
накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка
. Напряжение на участке
равно
; ток, текущий через этот участок, равен
. Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями
и
. Тогда это соединение можно рассматривать как проводник той же длины
, но с площадью сечения
. Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны
. Тогда:
откуда
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в
раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6).
Рис. 6. Смешанное соединение
Пусть В,
Ом,
Ом,
Ом,
Ом,
Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и
. Сопротивление участка
:
Ом.
Участок является параллельным соединением: два последовательно включённых резистора
и
подключены параллельно к резистору
. Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
A.
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
B;
B.
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и
находятся под напряжением
, поэтому:
A;
A.
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и
одинакова, так как они соединены последовательно:
А.
Стало быть, через резистор течёт ток
A.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Соединения проводников» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.
Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
А затем напряжение
Зная напряжения, найдем токи, протекающие через резисторы
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
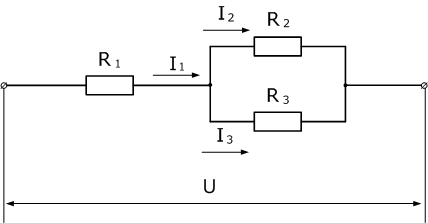
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи

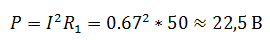
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
Таким образом производится расчет простых цепей постоянного тока.