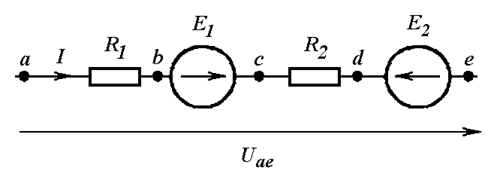
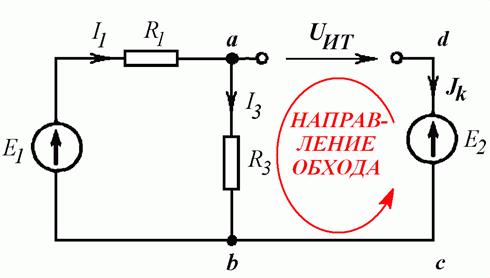
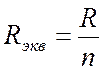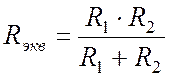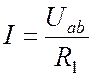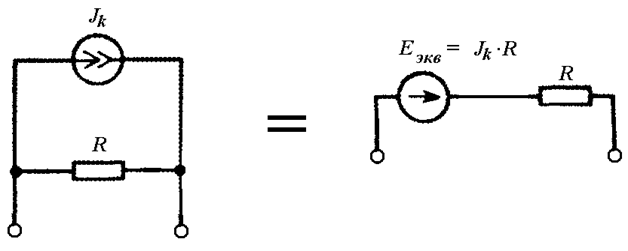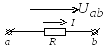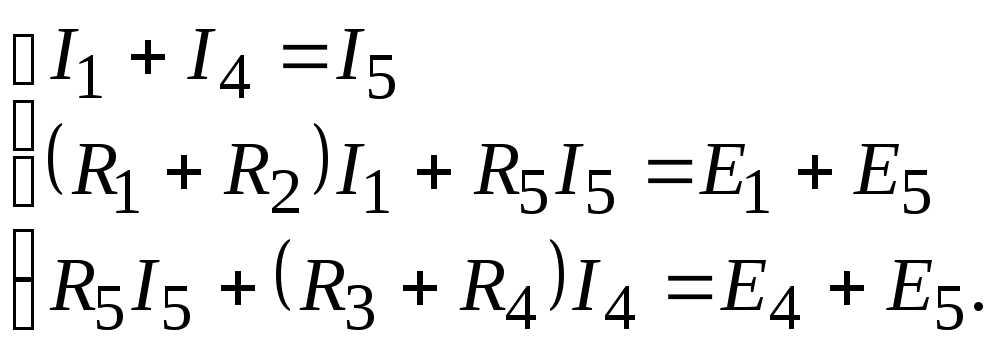Возьмем два участка цепи a—bи c—d (см.
рис. 1) и составим для них уравнения в комплексной форме с учетом указанных на
рис. 1 положительных направлений напряжений
и токов.


Объединяя оба случая, получим
 |
(1) |
или для постоянного тока
| (2) |
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка
цепи с источником ЭДС, согласно которому ток на участке цепи с источником
ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной
на сопротивление участка. В случае переменного тока все указанные величины суть
комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление
совпадает с выбранным направлением тока, и со знаком “-”, если их направление
противоположно направлению тока.
Основы символического метода расчета цепей
синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только
путем построения векторных диаграмм, но и аналитически – путем операций с комплексами,
символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством
векторных диаграмм является их наглядность, недостатком – малая точность графических
построений. Применение символического метода позволяет производить расчеты цепей
с большой степенью точности.
Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа
и законе Ома в комплексной форме.
Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно
такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только
токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных
величин.
1.
Первый закон Кирхгофа в комплексной форме:
| (3) |
2.
Второй закон Кирхгофа в комплексной форме:
| (4) |
или применительно к схемам замещения с источниками
ЭДС
| (5) |
3.
Соответственно матричная запись законов Кирхгофа в комплексной
форме имеет вид:
§
первый закон Кирхгофа:
| . |
(6) |
§
второй закон Кирхгофа
| (7) |
Пример.
Дано:
Рис. 2
Решение:
1.
.
2.

3.
.
4.
Принимая начальную фазу напряжения за нуль, запишем:
.
Тогда

5.
Поскольку ток распределяется обратно пропорционально сопротивлению
ветвей (это вытекает из закона Ома), то

6.
.
7.
Аналогичный результат можно получить, составив для данной схемы
уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров
схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными
на основании законов Кирхгофа. При этом необходимо составить и решить систему
с n неизвестными, что может оказаться
весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может
быть сокращено, если воспользоваться специальными методами расчета, к
которым относятся методы контурных токов и узловых потенциалов.
Метод контурных токов
Идея метода контурных токов: уравнения составляются только по второму закону
Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих
по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей
связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи
графа . Первый закон Кирхгофа выполняется автоматически.
Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя
бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.
Их выбор облегчает использование топологических понятий дерева и ветвей связи.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных
направлений перед началом расчета может не определять действительные направления
токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании
уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его
истинное направление противоположно.
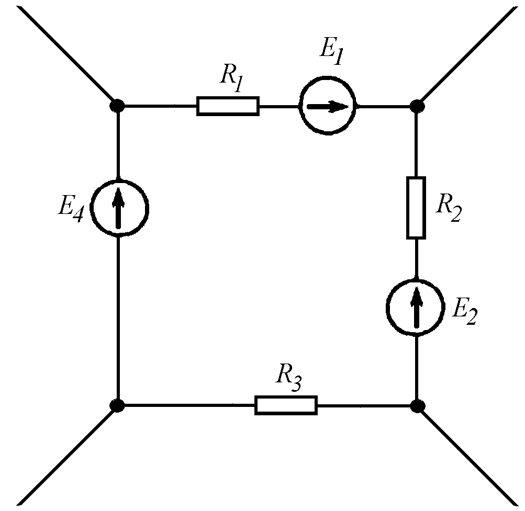
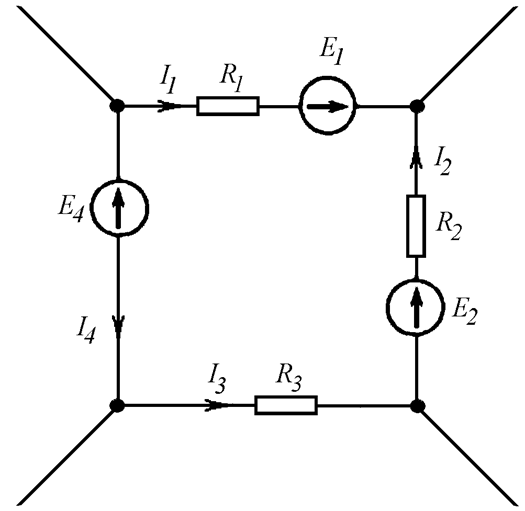
Пусть имеем схему по рис. 3.
Выразим токи ветвей через контурные токи:
;
;
;
;
.
Обойдя контур aeda, по второму закону Кирхгофа
имеем
.
Поскольку ,
то
.
Таким образом, получили уравнение для первого контура относительно контурных
токов. Аналогично можно составить уравнения для второго, третьего и четвертого
контуров:

совместно с первым решить их относительно контурных токов и затем по уравнениям,
связывающим контурные токи и токи ветвей, найти последние.
Однако данная система уравнений может быть составлена формальным путем:

При составлении уравнений необходимо помнить следующее:
— сумма сопротивлений, входящих в
i—й контур;
— сумма сопротивлений, общих для i—го и k—го контуров, причем
;
члены на главной диагонали всегда пишутся со знаком “+”;
знак “+” перед остальными членами ставится в случае, если через общее сопротивление
i—й и k—
й контурные токи проходят в одном направлении, в противном случае ставится знак
“-”;
если i—й и k— й контуры не имеют общих сопротивлений, то ;
в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в
контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением
контурного тока, и “-”, если не совпадает.
В нашем случае, для первого уравнения системы, имеем:
Следует обратить внимание на то, что, поскольку , коэффициенты контурных уравнений всегда
симметричны относительно главной диагонали.
Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются
в левых частях уравнений как известные контурные токи: k— й контурный ток, проходящий через ветвь с k—
м источником тока равен этому току .
Метод узловых потенциалов
Данный метод вытекает из первого закона Кирхгофа.
В качестве неизвестных принимаются потенциалы узлов, по найденным значениям
которых с помощью закона Ома для участка цепи с источником ЭДС затем находят
токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного
из узлов (любого) принимается равным нулю. Таким образом, число неизвестных
потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева
.
Пусть имеем схему по рис. 4, в которой примем
.
Допустим, что и
известны. Тогда значения токов на основании
закона Ома для участка цепи с источником ЭДС

Запишем уравнение по первому закону Кирхгофа для
узла а:
и подставим значения входящих
в него токов, определенных выше:
.
Сгруппировав соответствующие члены, получим:
.
Аналогично можно записать для узла b:
.
Как и по методу контурных токов, система уравнений
по методу узловых потенциалов может быть составлена формальным путем. При этом
необходимо руководствоваться следующими правилами:
1. В
левой части i—го
уравнения записывается со знаком “+”потенциал i—го узла, для которого составляется данное
i—е уравнение, умноженный на сумму проводимостей ветвей, присоединенных к данному i—му узлу, и со знаком “-”потенциал
соседних узлов, каждый из которых умножен
на сумму проводимостей ветвей, присоединенных к i—му
и k—му узлам.
Из сказанного следует, что все члены
, стоящие на главной диагонали в левой части
системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”,
причем . Последнее равенство по аналогии с методом
контурных токов обеспечивает симметрию коэффициентов уравнений относительно
главной диагонали.
2. В
правой части i—го
уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих
к i—му узлу, и проводимостей этих ветвей. При этом член суммы записывается
со знаком “+”, если соответствующая ЭДС направлена к i—му узлу, в противном случае ставится знак “-”. Если в подходящих
к i—му узлу ветвях содержатся источники тока,
то знаки токов источников токов, входящих в узловой ток простыми слагаемыми,
определяются аналогично.
В заключение отметим,
что выбор того или иного из рассмотренных методов определяется тем, что следует
найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений.
При расчете токов при одинаковом числе уравнений предпочтительнее использовать
метод контурных токов, так как он не требует дополнительных вычислений с использованием
закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных
цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1.
Основы теории
цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е
изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2.
Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с
.
Контрольные вопросы и задачи
1. В
ветви на рис. 1
. Определить ток
.
Ответ: .
2. В
чем заключается сущность символического метода расчета цепей синусоидального
тока?
3. В
чем состоит сущность метода контурных токов?
4. В
чем состоит сущность метода узловых потенциалов?
5.
В цепи на рис. 5 ;
;
;
. Методом контурных токов определить комплексы
действующих значений токов ветвей.
Ответ: ;
;
.
6. В
цепи на рис. 6
. Рассчитать токи в ветвях, используя метод
узловых потенциалов.
Ответ: ;
;
;
;
;
;
.

Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
В методе узловых потенциалов за вспомогательные расчетные величины принимают потенциалы узлов схемы. При этом потенциалом одного из узлов задаются, обычно считая его равным нулю (заземляют). Этот узел называют опорным узлом. Затем для каждого узла схемы, кроме опорного узла, составляют систему уравнений методом узловых потенциалов. По найденным потенциалам узлов находят токи ветвей по обобщенному закону Ома (закону Ома для ветви с ЭДС).
Отметим, что метод узловых потенциалов без предварительного преобразования схемы не применим к схемам с взаимной индукцией.
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), не имеющих общего узла нужно применять особые способы составления системы уравнений метода узловых потенциалов.
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (+E, если идеальный источник ЭДС направлен от опорного узла и –E в противном случае).
Метод двух узлов является частным случаем метода узловых потенциалов. Он применяется для определения токов в ветвях схемы с двумя узлами и произвольным числом параллельных активных и пассивных ветвей.
Решение задач методом узловых потенциалов и методом двух узлов
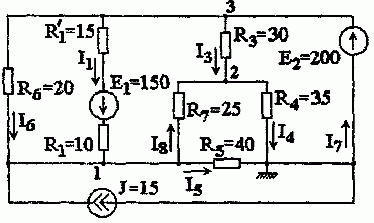
Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов.
Рис. 1.4.1
Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)
φ 4 =0.
Тогда
φ 3 = φ 4 + E 2 =200 B.
Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.
Рассматривая узел 1, получим
φ 1 ⋅ g 11 − φ 2 ⋅ g 12 − φ 3 ⋅ g 13 =J+ E 1 R 1 + R ′ 1
или
φ 1 ⋅ g 11 − φ 2 ⋅ g 12 =J+ E 1 R 1 + R ′ 1 + E 1 ⋅ g 13 .
В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E1 направлены к узлу 1.
Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим
Индивидуалка Лиза (25 лет) т.8 929 529-57-81 Москва, метро Полянка.
− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 − φ 3 ⋅ g 23 =0
или
− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = E 2 ⋅ g 23 .
Найдем собственную проводимость первого узла
g 11 = 1 R 6 + 1 R 1 + R ′ 1 + 1 R ИТ + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 =0,155 См.
Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока RИТ равно бесконечности.
Собственная проводимость узла 2
g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 =0,102 См.
Взаимные проводимости между узлами
g 13 = 1 R 6 + 1 R 1 + R ′ 1 = 1 20 + 1 25 =0,09 См; g 21 = g 12 = 1 R 2 = 1 25 =0,04 См; g 23 = 1 R 3 = 1 30 =0,033 См.
Подставив в уравнения известные величины, получим
{ φ 1 ⋅0,155− φ 2 ⋅0,04=39 − φ 1 ⋅0,04+ φ 2 ⋅0,102=6,6
Для решения этой системы используем метод определителей. Главный определитель системы
Δ=| 0,155 −0,04 −0,04 0,102 |=0,01421.
Частные определители
Δ 1 =| 39 −0,04 6,6 0,102 |=4,242; Δ 2 =| 0,155 39 −0,04 6,6 |=2,583.
Находим потенциалы узлов
φ 1 = Δ 1 Δ = 4,242 0,01421 =298,6 В; φ 2 = Δ 2 Δ = 2,583 0,01421 =181,8 В.
Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)
I 1 = φ 3 − φ 1 + E 1 R 1 + R ′ 1 = 200−298,6+150 10+15 =2,056 А.
В числителе этого выражения от потенциала узла 3, из которого вытекает ток I1, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.
Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)
I 1 = φ 3 − φ 1 R 6 = 200−298,6 20 =−4,93 А; I 2 = φ 1 − φ 2 R 2 = 298,6−181,8 25 =4,67 А; I 3 = φ 3 − φ 2 R 3 = 200−181,8 30 =0,607 А; I 4 = φ 2 − φ 4 R 4 = 181,8−0 35 =5,194 А.
Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I7. По первому закону Кирхгофа для узла 3 составим уравнение
− I 7 + I 3 + I 1 + I 6 =0.
Откуда
I 7 = I 3 + I 1 + I 6 =0,607+2,056−4,98=−2,317 A.
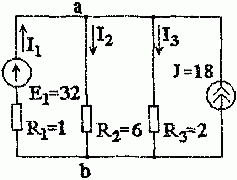
Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения.
Рис. 1.4.2
Решение
1 Находим напряжение между двумя узлами по методу двух узлов
U ab = φ a − φ b = E 1 ⋅ g 1 +J g 1 + g 2 + g 3 = 32⋅ 1 1 +18 1 1 + 1 6 + 1 2 =30 B.
При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус — если направлена от узла a к узлу b.
Аналогичное правило определяет и знаки токов источников тока.
2 Находим токи по закону Ома (по закону Ома для ветви с ЭДС)
I 1 = E 1 + φ b − φ a R 1 = E 1 − U ab R 1 = 32−30 1 =2 А; I 2 = U ab R 2 = 30 6 =5 А; I 3 = U ab R 3 = 30 2 =15 А.
Правильность решения проверим по первому закону Кирхгофа
I 1 − I 2 + I 3 +J=0; 2−5−15+18=0.
Метод узловых потенциалов в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

метод двух узлов,
метод узловых напряжений,
метод узловых потенциалов,
собственная проводимость,
взаимная проводимость
При свертке
параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из
сворачиваемых.
Если
параллельно соединены n одинаковых сопротивлений
(Рис. 3.3), эквивалентное сопротивление в n
раз меньше сопротивления любой из ветвей.
Рис. 3.3
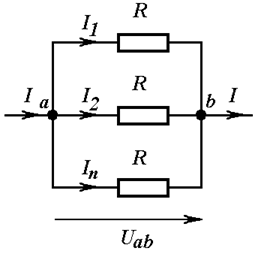
Если на
участке цепи параллельно соединены лишь два элемента (Рис. 3.4),
выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно
определить как отношение произведения двух сопротивлений к их сумме:
Рис. 3.4
4. ОСНОВНЫЕ ЗАКОНЫ
ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К основным
законам электрических цепей относятся закон Ома и законы Кирхгофа.
Закон Ома
Если в ветви
не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка
цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей
ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1):
Рис. 4.1
Закон Ома для
ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности
потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби,
знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение
на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви.
С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением
тока, с минусом – противоположные.
В частности,
ток в ветви, изображенной на Рис. 4.2, равен:
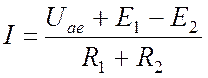
Рис. 4.2
Первый закон
Кирхгофа
В любом узле
цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к
узлу, принято считать положительными, токи, направленные от узла, принято считать
отрицательными (Рис. 4.3).
Рис. 4.3
По первому
закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема.
Но не все они будут независимыми. Если схема содержит узлов,
независимыми будут уравнений. Оставшееся
уравнение будет являться следствием всех предыдущих.
Второй закон
Кирхгофа
В любом
замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической
сумме ЭДС, включенных в контур.
При этом, положительными
считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура,
отрицательными считаются напряжения и ЭДС, которые противоположны направлению
обхода контура. Направление обхода контура можно выбирать произвольно.
Алгоритм
составления уравнения по второму закону Кирхгофа для замкнутого контура цепи
Для заданного
контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа
составляется в следующем порядке:
Рис. 4.4 а
- Задается направление токов в
ветвях (Рис. 4.4 б).
Рис. 4.4 б
- Выбирается направление обхода
контура (Рис. 4.4 в).
Рис. 4.4 в
- Записывается уравнение, в левой
части которого – сумма падений напряжений на сопротивлениях ветвей. В
правой части – сумма ЭДС контура.
Примечание:
Падение напряжения на сопротивлении ветви записывается в соответствии с
известным уже законом Ома (1.1):
Применение
второго закона Кирхгофа для незамкнутого участка цепи
Второй закон
Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый
участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве
незамкнутого участка.
Пример 4.1:
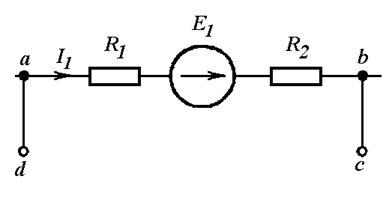
Незамкнутый
участок цепи abcd изображен на Рис. 4.5
а.
а)
б)
Рис. 4.5
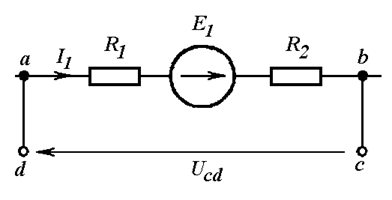
Дополняем
участок до замкнутого контура, добавляя напряжение между незамкнутыми точками c и d (Рис. 4.5 б). Теперь для контура abcd можно записать второй закон Корхгофа:
Применение
законов Кирхгофа при наличии в цепи источника тока
Источник тока
имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура
и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях
первого закона Кирхгофа источник тока должен содержаться обязательно.
При
необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего
источник тока, его заменяют напряжением на выводах источника тока.
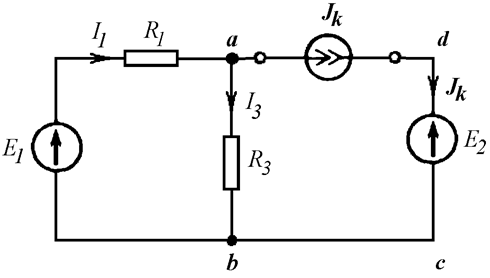
Пример 4.2:
Написать
уравнение по первому закону Кирхгофа для узла a
и уравнение по второму закону Кирхгофа для контура abcd (Рис. 4.6 а).
а)
б)
Рис. 4.6
Уравнение по
первому закону Кирхгофа для узла a содержит
источник тока и имеет вид:
Для того чтобы
написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его
выводах (Рис. 4.6 б), задаем направление обхода контура против
часовой стрелки и получаем:
Для упрощения
расчетов источник тока с параллельным сопротивлением можно заменить на
эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо
обязательно вернуться к исходной схеме.
Рис. 4.7
Независимый
контур цепи
В принципе, по
второму закону Кирхгофа можно составить столько уравнений, сколько контуров
содержит цепь. Но не все эти уравнения будут независимыми. Для определения
независимости уравнений по второму закону Кирхгофа вводится такое понятие как
независимый контур цепи.
Независимый
контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не
вошедшую в другие контуры цепи.
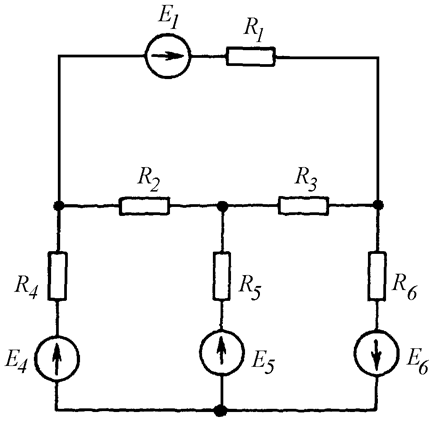
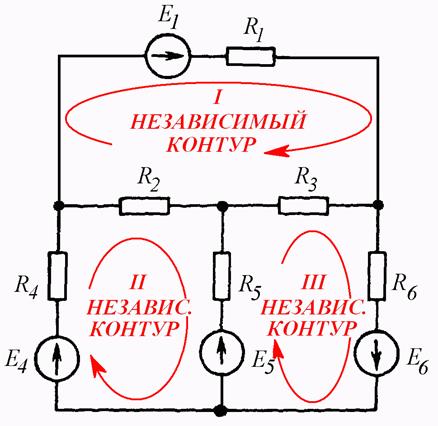
Независимые
контуры в общем случае выбираются произвольно, но проще всего выбирать их так,
чтобы они совпадали с ячейками цепи (Рис. 4.8 б).
а)
б)
Рис. 4.8
Если схема
содержит ветвей и
узлов,
число независимых контуров равно
.
Схема на Рис. 4.8 б
содержит три независимых контура.
5. СИСТЕМА
УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ
Законы
Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование
при этом – получение системы независимых уравнений, в которой число неизвестных
равно количеству токов, подлежащих определению.
Алгоритм
составления системы уравнений по законам Кирхгофа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
6
ЛЕКЦИЯ №2
1.3.
Напряжение на участке цепи
Под
напряжением на некотором участке
электрической цепи понимают разность
потенциалов между крайними точками
этого участка.
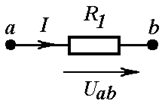
Рассмотрим
участок цепи с одним сопротивлением
(рис. 1.4).
Рис. 1.4. Схема
участка цепи
,
или
.
(1.1)
Эта
формула является законом Ома для участка
цепи без ЭДС.
Положительное
направление падения напряжения на
каком-либо участке цепи, указываемое
на схеме стрелкой, всегда совпадает с
положительным направлением отсчета
тока, протекающего по данному сопротивлению.
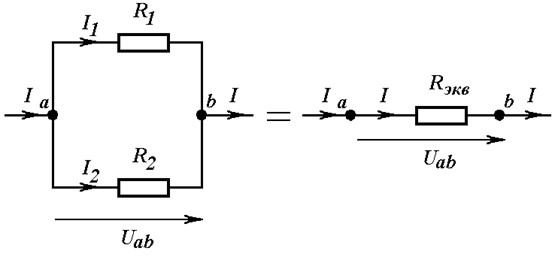
Если
цепь содержит ЭДС (рис. 1.5), то закон Ома
для участка цепи можно записать:
для
первого участка
;
для
второго участка
.
Отсюда
вытекает, что
. (1.2)
Это
формула закона Ома для участка цепи с
ЭДС (обобщенный закон Ома).
1.4.
Законы Кирхгофа. Составление уравнений
для расчета токов
с
помощью законов Кирхгофа
Для
расчета сложной разветвленной
электрической цепи существенное значение
имеет число ветвей и узлов.
Ветвью
называется участок электрической цепи,
состоящий только из последовательно
включенных источников ЭДС и приемников.
Узлом называется место или точка
соединения трех или более ветвей. При
обходе по соединенным в узлах ветвям
можно получить замкнутый контур
электрической цепи.
Все
электрические цепи подчиняются двум
законам Кирхгофа.
Первый
закон имеет две формулировки:
1)
алгебраическая сумма токов в узле равна
нулю;
2) сумма
токов, притекающих к любому узлу, равна
сумме токов, вытекающих из него
(1.3)
Физически
I закон Кирхгофа означает, что движение
зарядов в цепи происходит так, что ни в
одном из узлов (участков схемы) они не
накапливаются.
Второй
закон Кирхгофа гласит:
алгебраическая
сумма падений напряжений в любом
замкнутом контуре равна алгебраической
сумме ЭДС вдоль того же контура
(1.4)
где
m
– число сопротивлений в контуре;
n
– число ЭДС в контуре.
Если
направления падений напряжений и ЭДС
совпадают с направлением обхода контура,
то они входят в сумму со знаком « + ».
Законы
Кирхгофа используют для определения
токов в ветвях схемы.
Обозначим
число ветвей схемы – b,
число узлов – y,
число ветвей, содержащих источники тока
– bит.
В каждой ветви протекает свой ток.
Так
как токи в ветвях с источниками тока
известны, то число неизвестных токов
равно b
– bит.
Перед
составлением уравнений необходимо:
1)
произвольно выбрать положительные
направления токов в ветвях;
2)
выбрать положительные направления
обхода контуров для составления уравнений
по II закону Кирхгофа (с целью единообразия
рекомендуется для всех контуров выбирать
одно направление, например, по часовой
стрелке).
Для
получения линейно независимых уравнений
по I закону Кирхгофа составляют (y
– 1) уравнение, а по II закону – недостающие
(b
– bит)
– (y
– 1) уравнения. Составляя уравнения по
II закону Кирхгофа, необходимо охватить
все ветви схемы, исключая ветви с
источниками тока. При этом в каждый
контур должна входить хотя бы одна
ветвь, не вошедшая в предыдущий контур.
Такие контуры называются независимыми.
Это условие является необходимым и
достаточным для однозначного определения
токов.
Рассмотрим
уравнения для расчета токов на примере
схемы, изображенной на рис. 1.6.
2
y
II
– 1 = 2
b
J
– bит
= 4
п
о I закону – 2 уравнения
п
I
о II закону – 2 уравнения
1
3
Рис. 1.6. Пример
расчетной схемы
Узел
2 .
Узел
3 .
Контур
I .
Контур
II .
1.5.
Энергетический баланс в электрических
цепях
При
протекании токов по сопротивлениям
электрическая энергия преобразуется
в тепловую. На основании закона сохранения
энергии количество тепла, выделяющегося
в единицу времени в сопротивлениях
электрической цепи, равняется энергии,
доставляемой за то же время источниками
питания.
Если
направление тока I,
протекающего через источник ЭДС E,
совпадает с направлением ЭДС, то источник
ЭДС доставляет в цепь в единицу времени
энергию (его мощность), равную EI,
которая с положительным знаком входит
в уравнение энергетического баланса.
Уравнение
энергетического баланса
,
(1.5)
где
UabJk
– мощность, доставляемая в цепь источником
тока (a
– узел, к которому притекает ток Jk,
b
– узел, из которого этот ток вытекает).
1.6.
Метод пропорциональных величин
В
самой удаленной части схемы (ветви),
которую называют исходной, произвольно
задаются некоторым током, например, 1
А. Далее, продвигаясь от конца схемы к
началу, находят токи в ветвях и напряжения
на различных участках схемы. В результате
расчета получают значение напряжения
в начале схемы и токов в ветвях, если бы
в исходной ветви протекал ток 1 А.
Так
как найденное напряжение в начале схемы
в общем случае не будет равно ЭДС
источника, то следует во всех ветвях
изменить токи, умножив их на коэффициент,
равный отношению ЭДС источника к
найденному значению напряжения в начале
схемы.
Этот
метод применим только для расчета цепей,
состоящих из сопротивлений, соединенных
параллельно и последовательно, и одного
источника ЭДС.
1.7.
Метод контурных токов
В
основу метода положено два предположения:
1)
в каждом независимом контуре протекает
свой контурный ток;
2)
токи в ветвях схемы равны алгебраической
сумме контурных токов, протекающих
через данную ветвь.
Согласно
с этим методом неизвестными являются
контурные токи, поэтому число уравнений
для решения снижается до числа независимых
контуров, т.е. до числа уравнений
составленных по II закону Кирхгофа.
Рассмотрим
двухконтурную электрическую цепь (рис.
1.7).
Составим
уравнения по законам Кирхгофа
Подставим
в последние уравнения ток I5
Эти
уравнения можно записать в виде
где
и
– полные или собственные сопротивления
I
и II
контуров;
– сопротивление смежной ветви между
контурами I
и II;
и
– контурные ЭДС I
и II
контуров.
Сопротивление
смежной ветви входит в уравнение со
знаком « + », если направление смежного
контурного тока в нем совпадает с
направлением собственного контурного
тока.
Если
в электрической схеме имеются источники
тока, то их можно заменить источниками
напряжения. Если проводимости источников
тока равны нулю, то в этом случае
целесообразно выбрать заданные токи
источников тока в качестве контурных.
При этом число уравнений сократится на
число заданных источников тока.
Если
в схеме n
контуров, то уравнения запишутся

В
матричной форме можно записать
,
где


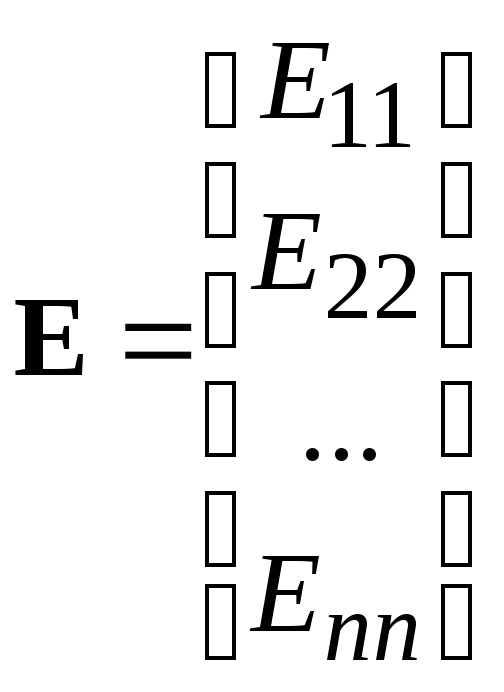
Общее
решение системы n
уравнений с n
неизвестными:
,
(1.7)
где
– определитель системы (1.6).
Алгебраическое
дополнение km
получено из
путем вычеркивания k-ого
столбца и m-й
строки и умножения полученного
определителя на
.
Относительно
главной диагонали определитель делится
на две части, являющиеся зеркальным
отображением друг друга. Это свойство
называется симметрией относительно
главной диагонали. Отсюда
.
Формула
(1.7) используется как исходная при
рассмотрении таких вопросов теории
линейных цепей как определение входных
и взаимных проводимостей ветвей, принцип
взаимности, метод наложения и линейные
соотношения в электрических цепях.
Соседние файлы в папке ТОЭ 1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
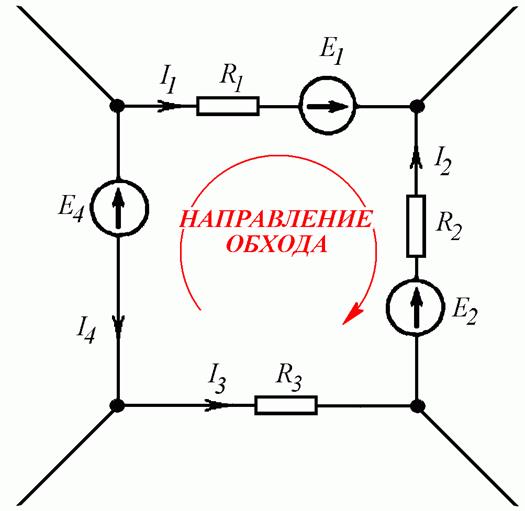
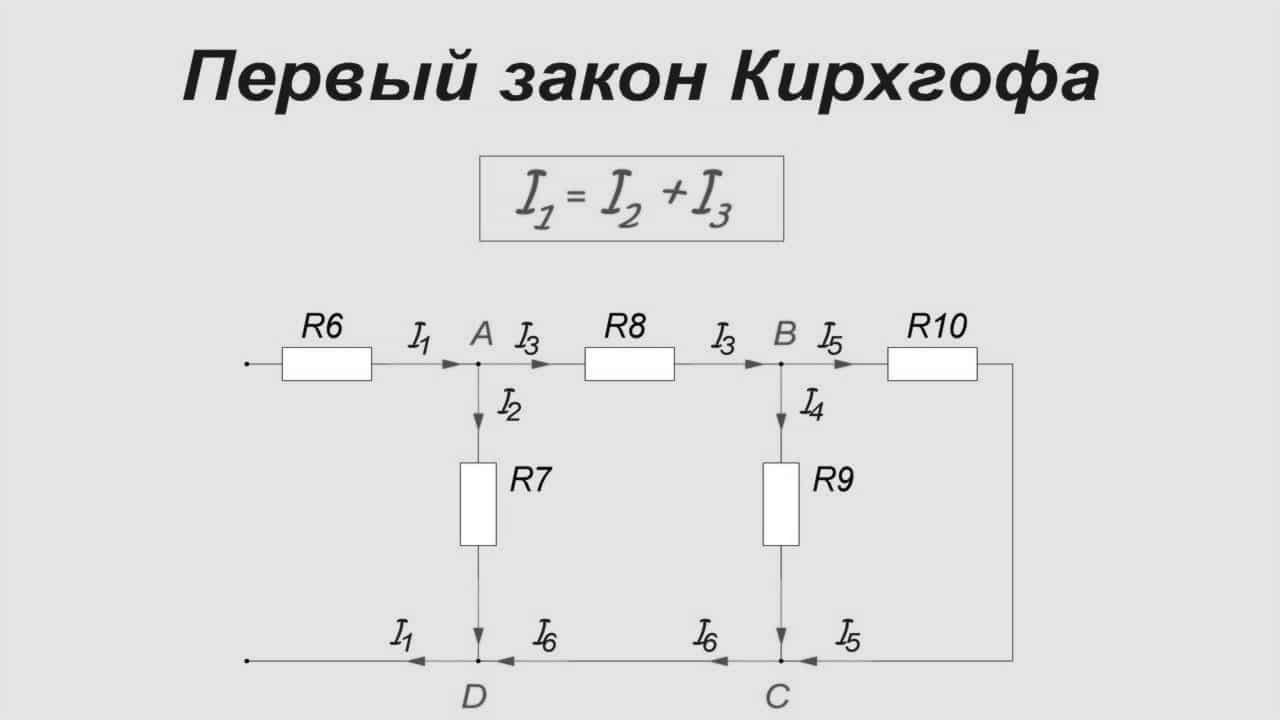
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
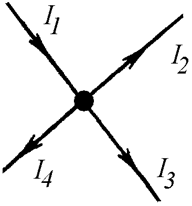
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
В частности: ∑Ф=0.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Примеры расчета цепей
Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i1, i2, i3, i4. Из них – два входящие ( i2, i3) и два исходящие из узла (i1, i4). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.
Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i1 + i2 + i3 – i4 = 0.
На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.
Рассмотрим алгоритм решения на примере рис. 5.
Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:
- 1 и 2.
- 1 и 3.
- 2 и 3.
Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I1 + I2 – I3 = 0.
Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.
Пишем уравнения:
- I1R1 + I3 R3 = E1;
- I2R2 + I3R3 = E2.
Решаем систему уравнений:
Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:
Решая эту систему, получим:
- I1 = 1,36 (значения в миллиамперах).
- I2 = 2,19 мА.;
- I3 = 3,55 мА.
Потенциал узла а равен: Ua = I3*R3 = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:
E1 – E2 + I1R1+ I2R2 = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).
Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.
Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.