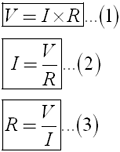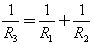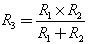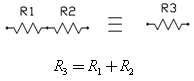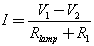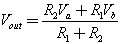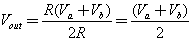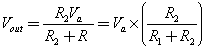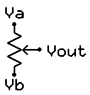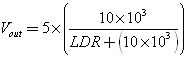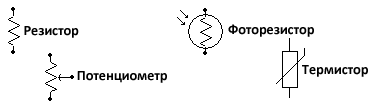Как найти напряжение на резисторе переменный ток

Резистор в цепи переменного тока

Пусть
цепь состоит из проводников с малой
индуктивностью и большим сопротивлением R (из
резисторов). Величина R называется активным
сопротивлением. Сопротивление R
в котором происходит превращение
электрической энергии в
другие виды энергии (в тепловую
энергию),
называют активным сопротивлением.

Итак,
в цепи имеется резистор, активное
сопротивление которого R, а катушка
индуктивности и конденсатор отсутствуют
(рис. 2.1).

Рис.
2.1.

Пусть
напряжение на концах цепи меняется по
гармоническому закону

Как
и в случае постоянного тока, мгновенное
значение силы тока прямо пропорционально
мгновенному значению напряжения. Поэтому
можно считать, что мгновенное значение
силы тока определяется законом Ома:

Следовательно,
в проводнике с активным сопротивлением
колебания силы тока по фазе совпадают
с колебаниями напряжения (рис. 2), а
амплитуда силы тока равна амплитуде
напряжения, деленной на сопротивление:

Рис.
2.2

При
небольших значениях частоты переменного
тока активное сопротивление проводника
не зависит от частоты и практически
совпадает с его электрическим
сопротивлением в цепи постоянного тока.

Катушка в цепи переменного тока

При
всяком изменении тока в электрической
цепи вследствие пересечения проводника
своим же собственным магнитным полем
в нем возникает индуктированная э. д.
с. Эту э. д. с. назвали э. д. с. самоиндукции.
Э. д. с. самоиндукции имеет реактивный
(реакция) характер. Так, например, при
увеличении тока в цепи э. д. с. самоиндукции
будет направлена против э. д. с. источника
напряжения, мешая току нарастать
(инерция) и поэтому ток в электрической
цепи не может установиться сразу. И,
наоборот, при уменьшении тока в цепи
индуктируется э. д. с. самоиндукции
такого направления, что, мешая току
исчезать, она поддерживает этот убывающий
ток. Э. Д. С. самоиндукции зависит от
скорости изменения тока в цепи и от
индуктивности этой цепи (числа витков,
наличия стальных сердечников).

e_L
= — LΔi/Δt.

В
цепи переменного тока э. д. с. самоиндукции
возникает непрерывно, так как ток в цепи
непрерывно изменяется. На рис.2.3
представлена схема цепи переменного
тока, содержащей катушку с индуктивностью
L без стального сердечника. Для простоты
будем считать сначала, что активное
сопротивление катушки очень мало и им
можно пренебречь.

Рис.2.3

При
изменениях силы тока по гармоническому
закону (рис. 2.3),

i
= I_m
cosωt,

в
катушке возникает ЭДС самоиндукции

e
= — Ldi/dt = I_m
Lω sinωt,

где L —
индуктивность катушки, ω
= 2πf —
циклическая частота переменного тока.

Так
как электрическое сопротивление катушки
равно нулю, то ЭДС самоиндукции в ней в
любой момент времени равна по модулю и
противоположна по знаку напряжению на
концах катушки, созданному внешним
генератором,

u
= — e_L
= — I_m
Lω sinωt.

Следовательно,
колебания напряжения на катушке
индуктивности опережают колебания силы
тока на π/2, или, что то же самое, колебания
силы тока отстают по фазе от колебаний
напряжения на π/2.

В
момент, когда напряжение на катушке
достигает максимума, сила тока равна
нулю (рис. 2.4). В момент, когда напряжение
становится равным нулю, сила тока
максимальна по модулю.

Рис.
2.4

Произведение

является
амплитудой колебаний напряжения на
катушке:

Отношение
амплитуды колебаний напряжения на
катушке к амплитуде колебаний силы тока
в ней называется индуктивным
сопротивлением (обозначается X_L):

Связь
амплитуды колебаний напряжения на
концах катушки с амплитудой колебаний
силы тока в ней совпадает по форме с
выражением закона Ома для участка цепи
постоянного тока:

Объясняется
это самоиндукцией. Возникающее при
нарастании силы тока электрическое
поле тормозит движение электронов. Вот
это противодействие нарастающему
току генератора и называется индуктивным
сопротивлением.

На
преодоление этого противодействия
затрачивается часть энергии переменного
тока генератора. Вся эта часть энергии
полностью превращается в энергию
магнитного поля катушки. Когда ток
генератора будет убывать, магнитное
поле катушки также будет убывать,
индуктируя в цепи ток самоиндукции.
Теперь ток самоиндукции будет идти в
одном направлении с убывающим током
генератора. Таким образом вся энергия
затраченная током генератора на
преодоление противодействия тока
самоиндукции катушки полностью вернулась
в цепь в виде энергии электрического
тока. Поэтому индуктивное сопротивление
является реактивным, т. е. не вызывающим
безвозвратных потерь энергии.

В
отличие от электрического сопротивления
проводника в цепи постоянного тока,
индуктивное сопротивление не является
постоянной величиной, характеризующей
данную катушку. Оно прямо пропорционально
частоте переменного тока. Поэтому
амплитуда колебаний силы тока в катушке
при постоянном значении амплитуды
колебаний напряжения должна убывать
обратно пропорционально частоте.
Постоянный ток вообще «не замечает»
индуктивности катушки. При ω = 0
индуктивное сопротивление равно нулю
(X_L =
0). Зависимость амплитуды колебаний силы
тока в катушке от частоты приложенного
напряжения можно наблюдать в опыте с
генератором переменного напряжения,
частоту которого можно изменять. Опыт
показывает, что увеличение в два раза
частоты переменного напряжения приводит
к уменьшению в два раза амплитуды
колебаний силы тока через катушку.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Условие квазистационарности
Резистор в цепи переменного тока
Конденсатор в цепи переменного тока
Катушка в цепи переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток — это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.

Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.

Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.

А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости и катушку индуктивности . Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.

Напряжение на клеммах источника меняется по закону:

(1)

Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?

Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным.

Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.

Текущее значение напряжения U(t) в момент времени называется мгновенным значением напряжения.

к оглавлению ▴

Условие квазистационарности

В случае переменного тока возникает один тонкий момент. Предположим, что цепь состоит из нескольких последовательно соединённых элементов.

Если напряжение источника меняется по синусоидальному закону, то сила тока не успевает мгновенно принимать одно и то же значение во всей цепи — на передачу взаимодействий между заряженными частицами вдоль цепи требуется некоторое время.

Между тем, как и в случае постоянного тока, нам хотелось бы считать силу тока одинаковой во всех элементах цепи. К счастью, во многих практически важных случаях мы действительно имеем на это право.

Возьмём, к примеру, переменное напряжение частоты nu = 50 Гц (это промышленный стандарт России и многих других стран). Период колебаний напряжения: с.

Взаимодействие между зарядами передаётся со скоростью света: м/с. За время, равное периоду колебаний, это взаимодействие распространится на расстояние:

м = 6000 км.

Поэтому в тех случаях, когда длина цепи на несколько порядков меньше данного расстояния, мы можем пренебречь временем распространения взаимодействия и считать, что сила тока мгновенно принимает одно и то же значение во всей цепи.

Теперь рассмотрим общий случай, когда напряжение колеблется с циклической частотой omega . Период колебаний равен , и за это время взаимодействие между зарядами передаётся на расстояние . Пусть — длина цепи. Мы можем пренебречь временем распространения взаимодействия, если много меньше :

(2)

Неравенство (2) называется условием квазистационарности. При выполнении этого условия можно считать, что сила тока в цепи мгновенно принимает одно и то же значение во всей цепи. Такой ток называется квазистационарным.

В дальнейшем мы подразумеваем, что переменный ток меняется достаточно медленно и его можно считать квазистационарным. Поэтому сила тока во всех последовательно включённых элементах цепи будет принимать одинаковое значение — своё в каждый момент времени. Оно называется мгновенным значением силы тока.

к оглавлению ▴

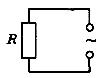
Резистор в цепи переменного тока

Простейшая цепь переменного тока получится, если к источнику переменного напряжения подключить обычный резистор (мы полагаем, разумеется, что индуктивность этого резистора пренебрежимо мала, так что эффект самоиндукции можно не принимать во внимание) , называемый также активным сопротивлением (рис. 1)

Рис. 1. Резистор в цепи переменного тока

Положительное направление обхода цепи выбираем против часовой стрелки, как показано на рисунке. Напомним, что сила тока считается положительной, если ток течёт в положительном направлении; в противном случае сила тока отрицательна.

Оказывается, мгновенные значения силы тока и напряжения связаны формулой, аналогичной закону Ома для постоянного тока:

$I = frac{displaystyle U}{displaystyle R vphantom{1^a}} = frac{displaystyle U_0}{displaystyle R vphantom{1^a}} sin omega t.$

Таким образом, сила тока в резисторе также меняется по закону синуса:

Амплитуда тока I_0 равна отношению амплитуды напряжения U_0 к сопротивлению :

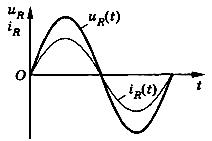
$I_0 = frac{displaystyle U_0}{displaystyle R vphantom{1^a}}.$

Мы видим, что сила тока через резистор и напряжение на нём меняются «синхронно», точнее говоря — синфазно (рис. 2).

Рис. 2. Ток через резистор совпадает по фазе с напряжением

Фаза тока равна фазе напряжения, то есть сдвиг фаз между током и напряжением равен нулю.

к оглавлению ▴

Конденсатор в цепи переменного тока

Постоянный ток через конденсатор не течёт — для постоянного тока конденсатор является разрывом цепи. Однако переменному току конденсатор не помеха! Протекание переменного тока через конденсатор обеспечивается периодическим изменением заряда на его пластинах.

Рассмотрим конденсатор ёмкости , подключённый к источнику синусоидального напряжения (рис. 3). Активное сопротивление проводов, как всегда, считаем равным нулю. Положительное направление обхода цепи снова выбираем против часовой стрелки.

Рис. 3. Конденсатор в цепи переменного тока

Как и ранее, обозначим через заряд той пластины конденсатора, на которую течёт положительный ток — в данном случае это будет правая пластина. Тогда знак величины совпадает со знаком напряжения . Кроме того, как мы помним из предыдущего листка, при таком согласовании знака заряда и направления тока будет выполнено равенство .

Напряжение на конденсаторе равно напряжению источника:

$frac{displaystyle q}{displaystyle C vphantom{1^a}} = U = U_0 sin omega t.$

Отсюда

Дифференцируя это равенство по времени, находим силу тока через конденсатор:

$I = dot{q} = CU_0 omega cos omega t.$ (3)

Графики тока и напряжения представлены на рис. 4. Мы видим, что сила тока каждый раз достигает максимума на четверть периода раньше, чем напряжение. Это означает, что фаза силы тока на pi/2 больше фазы напряжения (ток опережает по фазе напряжение на pi/2 ).

Рис. 4. Ток через конденсатор опережает по фазе напряжение на pi/2

Найти сдвиг фаз между током и напряжением можно также с помощью формулы приведения:

$cos varphi = sin left ( varphi + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Используя её, получим из (3):

$I = CU_0 omegasin left ( omega t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

И теперь мы чётко видим, что фаза тока больше фазы напряжения на pi/2 .

Для амплитуды силы тока имеем:

$I_0 = CU_0 omega = frac{displaystyle U_0}{displaystyle 1/left ( omega C right ) vphantom{1^a}}.$

Таким образом, амплитуда силы тока связана с амплитудой напряжения соотношением, аналогичным закону Ома:

$I_0 = frac{displaystyle U_0}{displaystyle X_C vphantom{1^a}},$

где

$X_C = frac{displaystyle 1}{displaystyle omega C vphantom{1^a}}.$

Величина X_C называется ёмкостным сопротивлением конденсатора. Чем больше ёмкостное сопротивление конденсатора, тем меньше амплитуда тока, протекающего через него, и наоборот.

Ёмкостное сопротивление обратно пропорционально циклической частоте колебаний напряжения (тока) и ёмкости конденсатора. Попробуем понять физическую причину такой зависимости.

1. Чем больше частота колебаний (при фиксированной ёмкости ), тем за меньшее время по цепи проходит заряд CU_0 ; тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление. При ёмкостное сопротивление стремится к нулю: . Это означает, что для тока высокой частоты конденсатор фактически является коротким замыканием цепи.

Наоборот, при уменьшении частоты ёмкостное сопротивление увеличивается, и при имеем . Это неудивительно: случай отвечает постоянному току, а конденсатор для постоянного тока представляет собой бесконечное сопротивление (разрыв цепи).

2. Чем больше ёмкость конденсатора (при фиксированной частоте), тем больший заряд CU_0 проходит по цепи за то же время (за ту же четверть периода); тем больше амплитуда силы тока и тем меньше ёмкостное сопротивление.

Подчеркнём, что, в отличие от ситуации с резистором, мгновенные значения тока и напряжения в одни и те же моменты времени уже не будут удовлетворять соотношению, аналогичному закону Ома. Причина заключается в сдвиге фаз: напряжение меняется по закону синуса, а сила тока — по закону косинуса; эти функции не пропорциональны друг другу. Законом Ома связаны лишь амплитудные значения тока и напряжения.

к оглавлению ▴

Катушка в цепи переменного тока

Теперь подключим к нашему источнику переменного напряжения катушку индуктивности (рис. 5). Активное сопротивление катушки считается равным нулю.

Рис. 5. Катушка в цепи переменного тока

Казалось бы, при нулевом активном (или, как ещё говорят, омическом) сопротивлении через катушку должен потечь бесконечный ток. Однако катушка оказывает переменному току сопротивление иного рода.
Магнитное поле тока, меняющееся во времени, порождает в катушке вихревое электрическое поле $vec{E_B}$ , которое, оказывается, в точности уравновешивает кулоновское поле vec{E} движущихся зарядов:

$vec{E} + vec{E_B} = vec{0}.$ (4)

Работа кулоновского поля vec{E} по перемещению единичного положительного заряда по внешней цепи в положительном направлении — это как раз напряжение . Аналогичная работа вихревого поля — это ЭДС индукции .

Поэтому из (4) получаем:

(5)

Равенство (5) можно объяснить и с энергетической точки зрения. Допустим, что оно не выполняется. Тогда при перемещении заряда по цепи совершается ненулевая работа, которая должна превращаться в тепло. Но тепловая мощность I^2R равна нулю при нулевом омическом сопротивлении цепи. Возникшее противоречие показывает, что равенство (5) обязано выполняться.

Вспоминая закон Фарадея $mathcal E_i = -L dot{I}$ , переписываем соотношение (5):

откуда

$dot{I} = frac{displaystyle U}{displaystyle L vphantom{1^a}} = frac{displaystyle U_0}{displaystyle L vphantom{1^a}} sin omega t.$ (6)

Остаётся выяснить, какую функцию, меняющуюся по гармоническому закону, надо продифференцировать, чтобы получить правую часть выражения (6). Сообразить это нетрудно (продифференцируйте и проверьте!):

$I = -frac{displaystyle U_0}{displaystyle omega L vphantom{1^a}} cos omega t.$ (7)

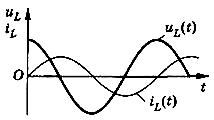
Мы получили выражение для силы тока через катушку. Графики тока и напряжения представлены на рис. 6.

Рис. 6. Ток через катушку отстаёт по фазе от напряжения на pi/2

Как видим, сила тока достигает каждого своего максимума на четверть периода позже, чем напряжение. Это означает, что сила тока отстаёт по фазе от напряжения на pi/2 .

Определить сдвиг фаз можно и с помощью формулы приведения:

$sin left ( varphi -frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = -cos varphi.$

Получаем:

$I = frac{displaystyle U_0}{displaystyle omega L vphantom{1^a}} sin left ( omega t -frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ).$

Непосредственно видим, что фаза силы тока меньше фазы напряжения на pi/2 .

Амплитуда силы тока через катушку равна:

$I_0 = frac{displaystyle U_0}{displaystyle omega L vphantom{1^a}}.$

Это можно записать в виде, аналогичном закону Ома:

$I_0 = frac{displaystyle U_0}{displaystyle X_L vphantom{1^a}},$

где

Величина X_L называется индуктивным сопротивлением катушки. Это и есть то самое сопротивление, которое наша катушка оказывает переменному току (при нулевом омическом сопротивлении).

Индуктивное сопротивление катушки пропорционально её индуктивности и частоте колебаний. Обсудим физический смысл этой зависимости.

1. Чем больше индуктивность катушки, тем большая в ней возникает ЭДС индукции, противодействующая нарастанию тока; тем меньшего амплитудного значения достигнет сила тока. Это и означает, что X_L будет больше.

2. Чем больше частота, тем быстрее меняется ток, тем больше скорость изменения магнитного поля в катушке, и тем большая возникает в ней ЭДС индукции, препятствующая возрастанию тока. При имеем , т. е. высокочастотный ток практически не проходит через катушку.

Наоборот, при имеем X_L = 0 . Для постоянного тока катушка является коротким замыканием цепи.

И снова мы видим, что закону Ома подчиняются лишь амплитудные, но не мгновенные значения тока и напряжения. Причина та же — наличие сдвига фаз.

Резистор, конденсатор и катушка, рассмотренные пока что по отдельности, теперь соберутся вместе в колебательный контур, подключённый к источнику переменного напряжения. Читайте следующий листок — «Переменный ток. 2».

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Переменный ток. 1» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

В идеальном колебательном контуре, то есть в контуре без
активного сопротивления, возникающие электромагнитные колебания могут
существовать бесконечно долго. Однако в реальных контурах всегда имеется нагрузка,
обладающее сопротивлением. Поэтому часть энергии контура всегда превращается во
внутреннюю энергию проводников. Проще говоря, реальные электромагнитные
колебания в контуре являются затухающими. Для того чтобы они были
незатухающими, необходимо компенсировались потери энергии при каждом полном
колебании в контуре.

Давайте с вами вспомним, что для механических колебаний это
достигалось путём воздействия внешней периодической силы. В результате в
системе возникали вынужденные колебания. Аналогично этому вынужденные
электромагнитные колебания в колебательном контуре происходят под действием
внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
При этом напряжение в цепи и сила тока изменяются как по знаку, так и по
модулю.

Ток, сила и направление которого периодически меняются,
называется переменным.

В настоящее время основная часть электроэнергии в мире
вырабатывается с помощью электромеханических индукционных генераторов
переменного тока, создающими синусоидальное напряжение.

Индукционным генератором переменного тока называется
устройство, предназначенное для преобразования механической энергии в энергию
переменного тока.

Как следует из названия устройства, принцип действия такого
генератора основан на явлении электромагнитной индукции. Основными частями
индукционного генератора переменного тока являются:

индуктор — это постоянный магнит или электромагнит,
который создаёт магнитное поле;

якорь — это обмотка, в которой индуцируется переменная
ЭДС;

и колле́ктор — это контактные кольца и скользящие
по ним контактные пластины (щётки). С помощью коллектора ток снимается или
подводится к вращающимся частям.

Давайте рассмотрим принцип действия простейшего индукционного
генератора на примере проводящей рамки с током, вращающейся в однородном
магнитном поле с постоянной угловой скоростью.

Пусть в начальный момент времени угол между нормалью к
плоскости рамки и линиями индукции магнитного поля равен нулю. Так как рамка вращается
с постоянной угловой скоростью, то данный угол будет меняться с течением
времени по линейному закону:

Тогда будет меняться и магнитный поток через поверхность,
ограниченную плоскостью рамки:

Поскольку магнитный поток, пронизывающий рамку, изменяется со
временем, то в ней согласно закону Фарадея индуцируется ЭДС индукции, равная
первой производной магнитного потока по времени, взятой с обратным знаком:

Произведение величин, стоящих перед функцией синуса есть
ничто иное, как амплитудное значение ЭДС индукции:

Отсюда следует, что изменение ЭДС индукции в контуре со
временем происходит по закону синуса:

Это достаточно легко проверить, если подключить выводы вращающейся
рамки к осциллографу. Нетрудно увидеть, что временная развёртка представляет
собой синусоиду.

Если к выводам рамки подключить нагрузку с достаточно большим
сопротивлением (намного большим, чем сопротивление рамки), то по ней будет
проходить переменный ток.

По закону Ома для полной цепи его сила будет также изменяться
по синусоидальному закону:

Анализируя последние два выражения, мы можем сделать вывод,
что в цепи, содержащей, кроме рамки, только сопротивление, колебания
напряжения и колебания силы тока совпадают по фазе, одновременно достигая
максимумов и минимумов.

Однако в общем случае (например, когда в цепи присутствует
конденсатор, или катушка, или то и другое одновременно) колебания силы тока в
цепи и напряжения будут происходить с одинаковой частотой, но не будут
совпадать по фазе:

Ещё раз обратим ваше внимание на то, что ток в цепи проходит
в одном направлении в течение полуоборота рамки, а затем меняет направление на
противоположное, которое также остаётся неизменным в течение следующего
полуоборота.

Промежуток времени, в течение которого ЭДС совершает одно
полное колебание, называется периодом переменного тока.

А число полных колебаний за одну секунду называется
частотой тока.

В электрических сетях большинства стран мира (в том числе и в
России) стандартная частота переменного тока равна 50 Гц. Продолжительность
периода такого тока составляет всего 0,02 с. Такая частота переменного тока
была выбрана с участием известного немецкого электротехника польско-русского
происхождения Михаила Осиповича Доливо-Добровольского.

Однако, например, в США, Канаде и некоторых других странах по
рекомендации известного сербского учёного Николы Тесла, стандартная частота
переменного тока равна 60 Гц.

Мы рассмотрели на схеме принцип работы генератора переменного
тока. Однако такой тип генераторов (с неподвижной магнитной системой и
вращающимся якорем) используется достаточно редко. Дело в том, что при помощи
подвижных контактов практически невозможно отводить от генератора ток высокого
напряжения из-за сильного искрения в контактах. Поэтому почти во всех
индукционных генераторах переменного тока якорь, в котором индуцируется ЭДС,
устанавливают неподвижно, а вращаться заставляют индуктор.

Вращающаяся часть генератора называется ротором. Он
располагается внутри неподвижной стальной станины цилиндрической формы,
называемой статором. Во внутренней части статора имеются специальные
пазы, в которые укладывается медный провод в виде витков. При вращении ротора в
этих витках и индуцируется переменный ток.

Ротор также имеет сложную форму и представляет собой стальной
сердечник с навитой на него обмоткой. По обмотке пропускается постоянный ток,
который подводится через щётки и кольца от постороннего источника постоянного
тока. Создаваемое этим током магнитное поле вращается вместе с ротором. При
этом силовые линии поля будут пересекать проводники, вложенные в пазы статора,
и индуцировать в них ЭДС.

Современные мощные генераторы вырабатывают напряжение до
15—20 кВ, а их коэффициент полезного действия может достигать 97—98 %.

Теперь давайте рассмотрим некоторые новые закономерности,
которые возникают в электрической цепи при её подключении к источнику
переменного тока. Итак, пусть источник создаёт переменно напряжение,
изменяющееся со временем по закону синуса:

По закону Ома для участка цепи, содержащим только
сопротивление, сила тока во всей цепи будет также изменяться по гармоническому
закону:

Максимальные величины напряжения и силы тока называются
амплитудными значениями напряжения и силы тока соответственно.

А значения напряжения и силы тока в любой момент времени
называются мгновенными.

Зная их, можно рассчитать мгновенную мощность переменного
тока, которая, в отличие от цепей постоянного тока, изменяется с течением
времени:

Под средней за период мощностью переменного тока понимают
отношение суммарной энергии, поступающей в цепь за период, к периоду.

С учётом зависимости силы тока от времени перепишем выражение
для мгновенной мощности на резисторе в цепи переменного тока:

Поскольку мгновенная мощность изменяется со временем, то
использовать эту величину на практике в качестве характеристики длительно
протекающих процессов очень неудобно. Давайте перепишем нашу формулу для
мощности немного по-другому (воспользовавшись знаниями из математики):

Как видим, в полученном уравнении первое слагаемое не зависит
от времени. А второе слагаемое — это переменная составляющая, являющаяся
функцией двойного угла. Её среднее значение за период (или время, кратное
периоду) равно нулю, поскольку половину периода косинус принимает положительные
значения, а вторую — отрицательные. Поэтому среднее значение мощности
переменного тока за время, большее чем период колебаний, можно найти как
половину произведения амплитудных значений силы тока и напряжения, или половину
произведения квадрата амплитудного значения силы тока и сопротивления:

Таким образом, сопротивление играет двоякую роль в цепи
переменного тока. Во-первых, оно ограничивает силу тока. А во-вторых, на
активном сопротивлении происходит безвозвратное превращение электроэнергии в
другие виды (в частности, во внутреннюю).

Выражение для средней мощности позволяет ввести действующие или
эффективные значения силы тока и напряжения, которые используются в качестве
основных характеристик переменного тока.

Действующее значение силы переменного тока равно силе
такого постоянного тока, который, проходя в электрической цепи по активному
сопротивлению, выделяет за промежуток времени, кратный периоду колебаний, такое
же количество теплоты, что и данный переменный ток.

Оно численно равно квадратному корню из среднего за период
значения квадрата силы переменного тока:

Аналогично можно ввести действующее значение для напряжения и
ЭДС:

Амперметры и вольтметры регистрируют именно действующие
значения силы тока и напряжения.

Для закрепления материала, решим с вами одну небольшую
задачу. Квадратная рамка площадью 500 см² вращается в однородном
магнитном поле с индукцией 10 мТл вокруг оси, лежащей в плоскости рамки и
перпендикулярной полю, совершая 25 оборотов в секунду. Определите действующее
значение силы тока в рамке, если её сопротивление равно 5 Ом.

В заключение урока отметим, что закон Ома для участка цепи
переменного тока, содержащего только резистор, выполняется как для амплитудных
и действующих, так и для мгновенных значений напряжения и силы тока вследствие
того, что их колебания совпадают по фазе.

Таким образом, резисторы оказывают сопротивление как
постоянному, так и переменному току, при этом в обоих случаях в них происходит
превращение электрической энергии в энергию теплового движения частиц.
Вследствие этого сопротивление резисторов получило название активного или
омического сопротивления.

Источник

В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.

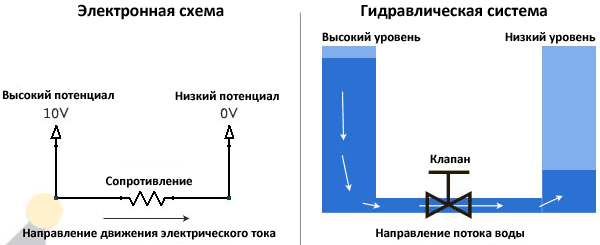
Представление об электричестве

Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.

Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору.
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда:
— Сколько тока втекает в узел, столько из него и вытекает
— Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы.
— Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь.
— Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.

Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.

Резистор

Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах. Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи.

Закон Ома

Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.

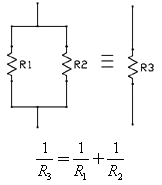
Последовательное и параллельное соединение резисторов

Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:

В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:

В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:

Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет.
Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути
электрическому току, снижая общее сопротивление цепи.

Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R₃=R₁+R₂

В интернете есть удобные он-лайн калькуляторы для расчета последовательного и параллельного соединения резисторов.

Токоограничивающий резистор

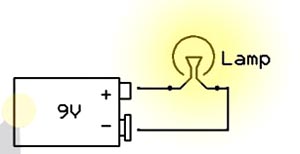
Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.

Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так:
I=(V₁-V₂)/R
где (V₁-V₂) является разностью напряжений до и после резистора.

Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой).

Математически это запишется так:

Из формулы следует, что ток уменьшится, если значение R1 увеличится. Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.

Вы можете воспользоваться он-лайн калькулятором для расчета токоограничительного резистора светодиода.

Резисторы как делитель напряжения

Как следует из названия, резисторы могут быть использованы в качестве делителя напряжения, другими словами, они могут быть использованы для уменьшения напряжения путем деления его. Формула:

Если оба резистора имеют одинаковое значение (R₁=R₂=R), то формулу можно записать так:

Другой распространенный тип делителя, когда один резистор подключен к земле (0В), как показано на рисунке 6B.
Заменив Vb на 0 в формуле 6А, получаем:

Узловой анализ

Теперь, когда вы начинаете работать с электронными схемами, важно уметь их анализировать и рассчитывать все необходимые напряжения, токи и сопротивления. Есть много способов для изучения электронных схем, и одним из наиболее распространенных методов является узловой, где вы просто применяете набор правил, и рассчитываете шаг за шагом все необходимые переменные.

Упрощенные правила узлового анализа

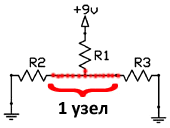
Определение узла

Узел – это любая точка соединения в цепи. Точки, которые связаны друг с другом, без других компонентов между ними рассматриваются как единый узел. Таким образом, бесконечное число проводников в одну точку считаются одним узлом. Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.

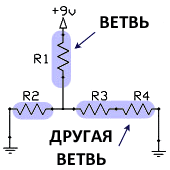
Определение ветви

Ветвь представляет собой набор из 1 и более компонентов, соединенных последовательно, и все компоненты, которые подсоединены последовательно к этой цепи, рассматриваются как одна ветвь.

Все напряжения обычно измеряются относительно земли напряжение на которой всегда равно 0 вольт.

Ток всегда течет от узла с более высоким напряжением на узел с более низким.

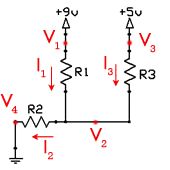
Напряжение на узле может быть высчитано из напряжения около узла, с помощью формулы:
V₁-V₂=I₁*(R₁)
Перенесем:
V₂=V₁-(I₁*R₁)
Где V₂ является искомым напряжением, V₁ является опорным напряжением, которое известно, I₁ ток, протекающий от узла 1 к узлу 2 и R₁ представляет собой сопротивление между 2 узлами.

Точно так же, как и в законе Ома, ток ответвления можно определить, если напряжение 2х соседних узлах и сопротивление известно:
I ₁=(V₁-V₂)/R₁

Текущий входящий ток узла равен текущему выходящему току, таким образом, это можно записать так: I ₁+ I₃=I₂

Важно, чтобы вы были в состоянии понимать смысл этих простых формул. Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1.
Используя соответствующие правила в нужный момент, вы сможете быстро и легко проанализировать схему и понять её. Это умение достигается практикой и опытом.

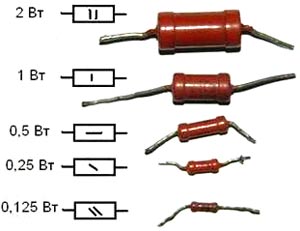
Расчет необходимой мощности резистора

При покупке резистора вам могут задать вопрос: «Резисторы какой мощности вы хотите?» или могут просто дать 0.25Вт резисторы, поскольку они являются наиболее популярными.
Пока вы работаете с сопротивлением больше 220 Ом, и ваш блок питания обеспечивает 9В или меньше, можно работать с 0.125Вт или 0.25Вт резисторами. Но если напряжение более 10В или значение сопротивления менее 220 Ом, вы должны рассчитать мощность резистора, или он может сгореть и испортить прибор. Чтобы вычислить необходимую мощность резистора, вы должны знать напряжение через резистор (V) и ток, протекающий через него (I):
P=I*V
где ток измеряется в амперах (А), напряжение в вольтах (В) и Р — рассеиваемая мощность в ваттах (Вт)

На фото предоставлены резисторы различной мощности, в основном они отличаются размером.

Разновидности резисторов

Резисторы могут быть разными, начиная от простых переменных резисторов (потенциометров) до реагирующих на температуру, свет и давление. Некоторые из них будут обсуждаться в этом разделе.

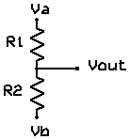
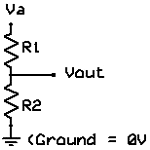
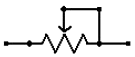
Переменный резистор (потенциометр)

На рисунке выше показано схематическое изображение переменного резистора. Он часто упоминается как потенциометр, потому что он может быть использован в качестве делителя напряжения.

Они различаются по размеру и форме, но все работают одинаково. Выводы справа и слева эквивалентны фиксированной точке (например, Va и Vb на рисунке выше слева), а средний вывод является подвижной частью потенциометра, а также используется для изменения соотношения сопротивления на левом и правом выводах. Следовательно, потенциометр относится к делителям напряжения, которым можно выставить любое напряжение от Va к Vb.
Кроме того, переменный резистор может быть использован как тока ограничивающий путем соединения выводов Vout и Vb, как на рисунке выше (справа). Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.

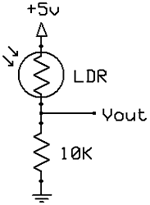
LDR (светочувствительные резисторы) и термисторы

Есть много датчиков основанных на резисторах, которые реагируют на свет, температуру или давление. Большинство из них включаются как часть делителя напряжения, которое изменяется в зависимости от сопротивления резисторов, изменяющегося под воздействием внешних факторов.

Терморезисторы

Фоторезистор (LDR)

Как вы можете видеть на рисунке 11A, фоторезисторы различаются по размеру, но все они являются резисторами, сопротивление которых уменьшается под воздействием света и увеличивается в темноте. К сожалению, фоторезисторы достаточно медленно реагируют на изменение уровня освещённости, имеют достаточно низкую точность, но очень просты в использовании и популярны. Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.

Как мы уже говорили, изменение сопротивления изменяет напряжение с делителя. Выходное напряжение можно рассчитать по формуле:

Если предположить, что сопротивление LDR изменяется от 10 МОм до 50 Ом, то V_out будет соответственно от 0.005В до 4.975В.

Термистор похож на фоторезистор, тем не менее, термисторы имею гораздо больше типов, чем фоторезисторы, например, термистор может быть либо с отрицательным температурным коэффициентом (NTC), сопротивление которого уменьшается с повышением температуры, или положительным температурным коэффициентом (PTC), сопротивление которого будет увеличиваться с повышением температуры. Сейчас термисторы реагируют на изменение параметров среды очень быстро и точно.

Схемотехническое обозначение резисторов

Про определение номинала резистора используя цветовую маркировку можно почитать здесь.

Оригинал статьи

Что такое падение напряжения на резисторе

Электрический ток, проходя по цепи, испытывает сопротивление, которое может изменяться под воздействием разнообразных условий внешней среды (экстремально низкие температуры или нагрев) и может зависеть от характеристик конкретного проводника. Например, чем тоньше проводник или длиннее – тем оно выше.

На значение его величины влияют следующие факторы:

сила тока;
длина проводящих частей;
напряжение;
материал проводниковых элементов;
нагрев (температура);
площадь поперечного сечения.

Резисторы можно разделить на постоянные, переменные и подстроечные. Главное их отличие друг от друга – возможность изменения показателя сопротивления. Чаще всего встречаются постоянные резисторы – данный показатель в них нельзя изменить, поэтому они и получили такое название. Переменные отличаются тем, что величину сопротивления в них можно настраивать. В подстроечном резисторе её также можно изменять, но отличие данной разновидности в том, что он не рассчитан на частое изменение параметра. Подстроечные резисторы выполняются в более компактном корпусе по сравнению с переменными.

Чтобы вычислить падение напряжения на резисторе, нужно помнить, что снижение нагрузки, приложенной ко всей цепи (то есть, напряжения, подключённого к контуру) может быть получено как для всего контура, так и для любого элемента цепи. Напряжение понижается за счёт сопротивления, которым обладают проводники.

Падение напряжения на резисторе зависит от силы проходящего тока и характеристик проводников. Температура и показатели тока также имеют значение. Например, напряжение, измеренное вольтметром на лампочке, подключённой к сети 220 В, будет немного ниже за счёт сопротивления, которым обладает лампочка.

Источники питания имеют разную величину напряжения. Это значение может превышать то, которое бывает необходимо на выходе. Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость в понижении вольтажа, в том числе с помощью резисторов.

Сравнительная таблица напряжений

Источник питания	Напряжение
NiCd аккумулятор	1,2 В
Литий-железо-фосфатный аккумулятор	3,3 В
Батарея типа «Крона»	9 В
Автомобильный аккумулятор	12 В
Аккумулятор для грузовых автомобилей	24 В

В этом случае резистор должен уменьшить протекающий по цепи ток. При этом ток не превращается в тепло, происходит именно его ограничение. То есть при включении резистора в цепь ток упадёт – в этом и состоит работа резистора, при совершении которой элемент нагревается.

В общем случае падения напряжения можно рассчитать, используя простую формулу, связывающее показатели между собой.

Но в ряде случаев, например, при параллельном подключении сопротивлений, посчитать необходимую величину уже сложнее. В этом случае по специальной формуле потребуется привести сопротивление параллельных веток к одному числу:

R = R1*R2 / (R1+R2)

При необходимости также учитываются другие сопротивления, суммирующиеся с этим значением (например, сопротивление провода и источника питания).

Физическое определение

Резистор — это элемент, использующийся в электрической цепи и не требующий для своей работы источника питания. Предназначен он для трансформирования силы тока в напряжение и обратно. Кроме этого, он может преобразовывать электрическую энергию в тепловую и ограничивать величину тока. Но перед расчётом падения напряжения на резисторе желательно разобраться в сути этого процесса.

Резистор — весьма распространённый элемент, характеризующийся рядом параметров. Основными из них являются:

сопротивление;
величина рассеиваемой энергии;
рабочее напряжение;
мощность;
устойчивость к влиянию окружающей среды;
паразитная составляющая.

Пассивный электрический элемент обозначается на схеме в виде прямоугольника с двумя выводами из середины его боковых сторон. В центре фигуры может указываться мощность римскими цифрами или чёрточками. Например, вертикальная полоска обозначает выдерживаемую мощность элемента, равную 1 Вт. Перечёркнутый прямоугольник в обозначениях на схеме указывает, что такой резистор является переменным.

Резисторы могут выпускаться с постоянным и переменным сопротивлением. Разновидностью вторых являются подстроечные элементы. Отличие их от переменных заключается лишь в способе установки нужного значения.

На схемах и в технической литературе устройство обозначается латинской буквой R, рядом с которой указывается порядковый номер и его номинал в соответствии с Международной системой единиц (СИ). Например, R12 5 кОм — резистор на пять килоом, расположенный в схеме под 12 номером.

При изготовлении элемента используется резистивный слой, который может быть плёночным или объёмным. Он наносится на диэлектрическое основание, а сверху покрывается защитной плёнкой.

Значение сопротивления

Сопротивление является фундаментальной величиной в электрических процессах. Его значение неизменно связано с током и напряжением. Их общая зависимость описывается с помощью закона Ома: сила тока, возникшая на участке цепи, прямо пропорциональна разности потенциалов между крайними точками этого участка и обратно пропорциональна его сопротивлению. Из этого закона находится сопротивление по следующей формуле:

R = U / I, где:

R — сопротивление на участке цепи, Ом.
I — сила тока, проходящая через этот участок, А.
U — разность потенциалов на узлах части схемы, В.

Фактически же сопротивление элемента определяется его физической структурой и обусловлено колебаниями атомов в кристаллической решётке. Поэтому все материалы различаются на проводники, полупроводники и диэлектрики в зависимости от способности проводить электричество.

Ток — это направленное движение носителей заряда. Для его возникновения необходимо, чтобы вещество имело свободные электроны. Если к такому физическому телу приложить электрическое поле, то перемещаемые им заряды начнутся сталкиваться с неоднородностями структуры. Эти дефекты образуются из-за различных примесей, нарушения периодичности решётки, тепловых флуктуаций. Ударяясь о них, электрон расходует энергию, которая преобразовывается в тепловую. В результате заряд теряет импульс, а величина разности потенциалов уменьшается.

Но закон Ома можно применить не для всех веществ. В электролитах, диэлектриках и полупроводниках линейная зависимость между тремя величинами наблюдается не всегда. Сопротивление таких веществ зависит от физических параметров проводника, а именно — его длины и площади поперечного сечения, при этом оно чувствительно к изменению температуры.

Эта зависимость описывается с помощью формулы R = p * l / S. То есть сопротивление прямо пропорционально длине и обратно пропорционально площади проводника. Величина p называется удельным сопротивлением и определяется типом материала. Его значение берётся из справочника.

Импеданс резистора

Закон Ома применим для идеального резистора, не обладающего паразитными сопротивлениями. Полное сопротивление (импеданс) определяется исходя из эквивалентной схемы. Точный расчёт сопротивления для понижения напряжения необходимо проводить по другим формулам. Эквивалентная схема резистора, кроме активного импеданса, содержит также ёмкостное и индуктивное сопротивление.

Первое приводит к медленному накоплению заряда, который рассеивается при изменении направления тока. Чем больше паразитная ёмкость, тем дольше она заряжается. Соответственно, чем быстрее ток изменяет своё направление, тем меньше его ёмкостное сопротивление. Второе же характеризуется магнитным полем, чье появление мешает току изменять направление, поэтому, чем быстрее ток изменяет своё движение, тем больше становится индуктивное сопротивление.

Импеданс вычисляется по формуле: I = U/Z, где Z = (R2+(Xc-Xl)2)½. Где:

R — активное значение, R = p*l/s.
Xc — ёмкостная величина, Хс = 1/w*C.
Xl — индуктивная величина, Хl = w*C.
w- циклическая частота, w = 2πƒ.

Зная полное сопротивление резистора, можно точнее рассчитать падение напряжения в нём. Но для измерения паразитных составляющих понадобится использовать узкоспециализированные приборы. В обычных расчётах сопротивление вычисляют, учитывая только его активное значение, а паразитные величины принимают за ничтожно малые.

Характеристика мощности резистора

Мощность электрического тока на участке цепи можно узнать через произведение силы тока для него и напряжения на данном участке. Формула имеет следующий вид:
P= I * U (произведение силы тока и напряжения), где

P – значение мощности (Вт).

Резистор совершает работу по снижению силы тока, при этом он выделяет тепло в окружающее пространство. Но если работа по ограничению тока очень велика и тепло вырабатывается слишком быстро, то он перегреется и может сгореть, так как не будет успевать его рассеивать. Следует учитывать этот момент, подбирая мощность резистора

Важно! Мощность резистора – это очень важный параметр, который обязательно нужно учитывать при разработке электрических схем устройств Мощность резистора характеризуется максимальной величиной силы тока, которую он может выдерживать без перегрева и не выходя из строя.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Как рассчитать сопротивление для понижения напряжения: формула падения на резисторе

Резистор является одним из самых распространённых элементов в электрической цепи. С его помощью ограничивается ток и изменяется напряжение. Конструируя схемы, часто может понадобится рассчитать сопротивление для понижения напряжения. Это актуально при построении делителей цифровых устройств или блоков питания, поэтому уметь выполнять такие вычисления должен каждый радиолюбитель.

Резистор — весьма распространённый элемент, характеризующийся рядом параметров. Основными из них являются:

сопротивление;
величина рассеиваемой энергии;
рабочее напряжение;
мощность;
устойчивость к влиянию окружающей среды;
паразитная составляющая.

Значение сопротивления

R = U / I, где:

R — сопротивление на участке цепи, Ом.
I — сила тока, проходящая через этот участок, А.
U — разность потенциалов на узлах части схемы, В.

Импеданс резистора

Импеданс вычисляется по формуле: I = U/Z, где Z = (R2+(Xc-Xl)2)½. Где:

R — активное значение, R = p*l/s.
Xc — ёмкостная величина, Хс = 1/w*C.
Xl — индуктивная величина, Хl = w*C.
w- циклическая частота, w = 2πƒ.

Параллельное соединение

В электрических схемах на участках цепи используется как параллельное, так и последовательное соединение. Первое представляет собой цепь, в которой каждый её элемент подключён к другому обоими контактами, но при этом между собственными его выводами нет прямой электрической связи. Т. е. существует две точки (электрические узлы), к которым присоединено несколько резисторов.

При таком включении ток, проходя через узел, начинает разделяться, и через каждый элемент потечёт разное его значение. Величина тока на каждом элементе будет прямо пропорциональна сопротивлению резистора, поэтому общая проводимость на этом участке увеличится, а её импеданс уменьшится.

Формула, с помощью которой можно рассчитать общую проводимость, выглядит так: G = 1/ Rобщ = 1/ R1 + 1/ R2 +…+ 1/ Rn, где n — обозначает порядковый номер резистора в цепи.

Преобразовав эту формулу, получится выражение вида: R общ = 1/G = (R1*R2*…* Rn) / (R1*R2 + R2*Rn +…+ R1*Rn. Проанализировав его, можно сделать вывод, что при параллельном соединении импеданс всегда будет меньше самого маленького значения отдельного резистора.

При таком соединении напряжение между узлами одновременно является общей разностью потенциалов для всего участка и на каждом отдельно взятом резисторе. Поэтому если рассчитать падение напряжения на одном приборе, то оно будет таким же на любом параллельно подключённом элементе: U общ = U 1 = U 2 =…= U n.

А вот электрический ток, проходящий через отдельный элемент, исходя из закона Ома будет равен: I Rn = U Rn / R n.

Последовательное включение

Так называется объединение в один участок цепи двух или более резисторов, в котором их соединение между собой происходит только в одной точке. Импеданс при последовательном включении определяется как сумма сопротивлений каждого отдельного элемента: Rобщ = R1+R2+…+Rn.

Следовательно, ток, протекающий через такую цепочку, будет становиться всё меньше после прохождения через последовательно включённый резистор. Чем будет больше элементов в цепи, тем труднее ему будет пройти их всех. Таким образом, его общее значение определяется как Iобщ = U / (R1+R2+…+Rn).

Поэтому можно утверждать, что в последовательном соединении существует только один путь для протекания тока. Чем будет больше количество резисторов в линии, тем меньше будет ток на этом участке.

Падение разности потенциалов при таком типе соединения на каждом элементе будет иметь своё значение. Оно определяется формулой URn = IRn*Rn, и чем больше будет импеданс элемента, тем больше энергии в нём начнёт выделяться.

Расчёт делителя напряжения

Резистивный делитель напряжения представляет элементарную схему для понижения напряжения. Состоять он может из двух или более элементов. Простейший делитель можно представить в виде двух участков цепи, которые называют плечами. Одно из них, которое располагается между положительной точкой потенциала и нулевой, — верхнее, а другое, между отрицательной и минусовой, — нижнее.

Такая схема используется для снижения напряжения как в постоянных, так и переменных цепях. Суть процесса заключается в следующем.

На резистивную схему от источника питания подаётся напряжение U.
Через резисторы последовательного участка цепи, образованного резисторами R1 и R2, начинает протекать ток.
В результате на каждом из них выделяется какое-то количество энергии, т. е. возникает падение напряжения.

Сумма напряжений на всём размахе линии равняется значению разности потенциалов источника питания. В соответствии с формулой: U = I*R падение напряжения прямо пропорционально силе тока и величине сопротивления. Учитывая, что ток, протекающий через резисторы, одинаковый, справедливыми будут формулы U1 = I*R1 и U2= I*R2.

Тогда общее падение напряжение на участке будет равно U = I *(R1+ R2). Исходя из этого можно найти силу тока: I = U /(R1+ R2). Используя эти два выражения, можно получить окончательные формулы для расчёта падения напряжения на каждом элементе:

U1 = R1*U/(R1+R2);
U2 = R2*U/(R1+R2).

Практическое применение такого делителя очень распространено из-за несложности реализации понижения напряжения. Например, пусть источник питания выдаёт 12 В, а на нагрузку необходимо подать 6 В, при этом её сопротивление составляет 10 кОм. Для решения такой задачи рекомендуется использовать резисторы, сопротивление которых в десять раз меньше нагрузочного значения, поэтому, приняв R 1 = 1 кОм и подставив все известные значения в формулу напряжения на резисторе, получится, что 6 = R 2*12 (1000+ R 2) отсюда R 2 = 1 кОм.

Теперь, зная все величины, можно проверить верность расчёта. Падение разности потенциалов на первом элементе высчитывается как U 1 = 1000*12/(1000+1000) = 6 В, а общее напряжение — Uобщ = U 1+ U 2 = 12 В, что соответствует значению источника питания.

Следует отметить, что использование резисторов для понижения используется только при маломощных нагрузках, так как часть энергии превращается в тепло, а коэффициент полезного действия (КПД) очень низкий.

Определение силы тока на резисторе при разных типах соединения

Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.
I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.

В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.

Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.

Как понизить напряжение с помощью резистора

Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость снизить входное напряжение. Проще всего этого можно добиться, используя схему с двумя резисторами, более известную как делитель напряжения. Классическая схема выглядит так:

В этом случае напряжение подаётся на два резистора с использованием параллельного подключени, а на выходе его получают с одного. Подбор номиналов резисторов осуществляют по формуле так, чтобы напряжение, снимаемое на выходе, составляло какую-то часть от подаваемого. Расчет резистора для понижения напряжения можно воспользовавшись формулой, основанной на законе Ома:

Uвых= (Uвх*R2)/(R1+R2), где

Uвх – напряжение на входе, В;

Uвых – напряжение на выходе, В

R1 – показатель сопр. 1-ого резистора (Ом)

R2 – показатель сопр. 2-ого элемента, (Ом)

Подбор резистора для понижения напряжения

Для подбора нужного сопротивления резистора можно воспользоваться готовыми онлайн-калькуляторами или программами для моделирования работы электронных схем. Симуляторы электрических цепей способны не только рассчитать напряжение на выходе в зависимости от сопротивления элементов и способа их подключения, но и обладают функционалом, позволяющим визуализировать то, как падает ток и напряжение на резисторе. Например, приложение EveryCircuit позволяет изменять в схеме параметры элементов, выбирать скорость симуляции, получать данные в различных точках. При этом можно наблюдать за динамикой изменения значений, используя для ввода входных параметров вращающийся лимб в нижнем правом углу.

Существует ещё ряд бесплатных программ для эмуляции, позволяющие выполнить, в том числе, расчёт резистора при понижении напряжения, например:

EasyEDA;
Circuit Sims;
DcAcLab;

и другие.

В статье мы ознакомились с понятием сопротивления, узнали о его единицах измерения, о маркировке резисторов, о программах эмулирующих работу цепи и облегчающих подбор нужного сопротивления, а также рассмотрели примеры расчёта падения напряжения на резисторе.

Какое напряжение после резистора

Есть другой способ снижения напряжения на нагрузке, но только для цепей постоянного тока. Про смотри здесь.

Вместо дополнительного резистора используют цепочку из последовательно включенных, в прямом направлении, диодов.

Весь смысл состоит в том, что при протекании тока через диод на нем падает «прямое напряжение» равное, в зависимости от типа диода, мощности и тока протекающего через него — от 0,5 до 1,2 Волта.

На германиевом диоде падает напряжение 0,5 — 0,7 В, на кремниевом от 0,6 до 1,2 Вольта. Исходя из того, на сколько вольт нужно понизить напряжение на нагрузке, включают соответствующее количество диодов.

Чтобы понизить напряжение на 6 В необходимо приблизительно включить: 6 В: 1,0 = 6 штук кремниевых диодов, 6 В: 0,6 = 10 штук германиевых диодов. Наиболее популярны и доступны кремниевые диоды.

Выше приведенная схема с диодами, более громоздка в исполнении, чем с простым резистором. Но, выходное напряжение, в схеме с диодами, более стабильно и слабо зависит от нагрузки. В чем разница между этими двумя способами снижения выходного напряжения?

У резистора (проволочного сопротивления) линейная зависимость между током, проходящем через него и падением напряжения на нем. Во сколько раз увеличится ток, во столько же раз увеличится и падение напряжения на резисторе.

Из примера 1: если мы к лампочке подключим параллельно еще одну, то ток в цепи увеличится, с учетом общего сопротивления двух лампочек до 0,66 А. Падение напряжения на добавочном резисторе будет: 12 Ом *0,66 А = 7,92 В. На лампочках останется: 12 В — 7,92 В = 4,08 В. Они будут гореть в пол накала.

Совсем другая картина будет если вместо резистора будет цепочка диодов.

Зависимость между током протекающем через диод и падающем на нем напряжении нелинейная. Ток может увеличиться в несколько раз, падение напряжения на диоде увеличится всего на несколько десятых вольта.

Т.е. чем больше ток диода, тем (сравнительно с резистором) меньше увеличивается его сопротивление. Падение напряжения на диодах мало зависит от тока в цепи.

Диоды в такой цепи выполняют роль стабилизатора напряжения. Диоды необходимо подбирать по максимальному току в цепи. Максимально допустимый ток диодов должен быть больше, чем ток в рассчитываемой цепи.

Падения напряжения на некоторых диодах при токе 0,5 А даны в таблице.

В цепях переменного тока, в качестве добавочного сопротивления можно использовать конденсатор, индуктивность, динистор или тиристор (с добавлением схемы управления).

Для человека, который знаком с электрооборудованием на уровне простого пользователя (знает, где и как включить/выключить), многие используемые электриками термины кажутся какой-то бессмыслицей. Например, чего только стоит «падение напряжения» или «сборка схемы». Куда и что падает? Кто разобрал схему на детали? На самом же деле, физический смысл происходящих процессов, скрывающийся за большинством этих слов, вполне доступен для понимания даже со школьными знаниями физики.

Чтобы объяснить, что такое падение напряжения, необходимо вспомнить, какие вообще напряжения бывают в (имеется в виду глобальная классификация). Их всего два вида. Первый — это напряжение который подключен к рассматриваемому контуру. Оно может также называться приложенным ко всей цепи. А второй вид — это именно падение напряжения. Может быть рассмотрено как в отношении всего контура, так и любого отдельно взятого элемента.

На практике это выглядит следующим образом. Например, если взять обычную вкрутить ее в патрон, а провода от него подключить в домашнюю сетевую розетку, то приложенное к цепи (источник питания — проводники — нагрузка) напряжение составит 220 Вольт. Но стоит нам с помощью вольтметра замерять его значение на лампе, как станет очевидно, что оно немного меньше, чем 220. Так произошло потому, что возникло падение напряжения на которым обладает лампа.

Пожалуй, нет человека, который не слышал бы о законе Ома. В общем случае формулировка его выглядит так:

где R — активное сопротивление цепи или ее элемента, измеряется в Омах; U — электрическое напряжение, в Вольтах; и, наконец, I — ток в Амперах. Как видно, все три величины непосредственно связаны между собой. Поэтому, зная любые две, можно довольно просто вычислить третью. Конечно, в каждом конкретном случае придется учесть род тока (переменный или постоянный) и некоторые другие уточняющие характеристики, но основа — вышеуказанная формула.

Электрическая энергия — это, фактически, движение по проводнику отрицательно заряженных частиц (электронов). В нашем примере спираль лампы обладает высоким сопротивлением, то есть замедляет перемещающиеся электроны.

Благодаря этому возникает видимое свечение, но общая энергия потока частиц снижается. Как видно из формулы, с уменьшением тока уменьшается и напряжение. Именно поэтому результаты замеров у розетки и на лампе различаются. Эта разница и является падением напряжения.

Данная величина всегда учитывается, чтобы предотвратить слишком большое снижение на элементах в конце схемы.

Падение напряжения на резисторе зависит от его и силы протекающего по нему тока. Также косвенное влияние оказывают температура и характеристики тока. Если в рассматриваемую цепь включить амперметр, то падение можно определить умножением значения тока на сопротивление лампы.

Но далеко не всегда удается вот так просто с помощью простейшей формулы и измерительного прибора выполнить расчет падения напряжения. В случае параллельно подключенных сопротивлений нахождение величины усложняется. На приходится дополнительно учитывать реактивную составляющую.

Рассмотрим пример с двумя параллельно включенными резисторами R1 и R2. Известно сопротивление провода R3 и источника питания R0. Также дано значение ЭДС — E.

Приводим параллельные ветки к одному числу. Для этой ситуации применяется формула:

R = (R1*R2) / (R1+R2)

Определяем сопротивление всей цепи через сумму R4 = R+R3.

Рассчитываем ток:

Остается узнать значение падение напряжения на выбраном элементе:

Здесь множитель «R5» может быть любым R — от 1 до 4, в зависимости от того, какой именно элемент схемы нужно рассчитать.

Итак, резистор… Базовый элемент построения электрической цепи.

Работа резистора заключается в ограничении тока, протекающего по цепи. НЕ в превращении тока в тепло, а именно в ограничении тока. То есть, без резистора по цепи течет большой ток, встроили резистор – ток уменьшился. В этом заключается его работа, совершая которую данный элемент электрической цепи выделяет тепло.

Пример с лампочкой

Рассмотрим работу резистора на примере лампочки на схеме ниже. Имеем источник питания, лампочку, амперметр, измеряющий ток, проходящий через цепь. И Резистор. Когда резистор в цепи отсутствует, через лампочку по цепи побежит большой ток, например, 0,75А.

Лампочка горит ярко. Встроили в цепь резистор — у тока появился труднопреодолимый барьер, протекающий по цепи ток снизился до 0,2А. Лампочка горит менее ярко. Стоит отметить, что яркость, с которой горит лампочка, зависит так же и от напряжения на ней. Чем выше напряжение — тем ярче.

Кроме того, на резисторе происходит падение напряжения. Барьер не только задерживает ток, но и «съедает» часть напряжения, приложенного источником питания к цепи. Рассмотрим это падение на рисунке ниже. Имеем источник питания на 12 вольт.

На всякий случай амперметр, два вольтметра про запас, лампочку и резистор. Включаем цепь без резистора(слева). Напряжение на лампочке 12 вольт. Подключаем резистор — часть напряжения упала на нем. Вольтметр(снизу на схеме справа) показывает 5В.

На лампочку остались остальные 12В-5В=7В. Вольтметр на лампочке показал 7В.

Разумеется, оба примера являются абстрактными, неточными в плане чисел и рассчитаны на объяснение сути процесса, происходящего в резисторе.

Единица измерения сопротивления резистора

Основная характеристика резистора — сопротивление. Единица измерения сопротивления — Ом (Ohm, Ω). Чем больше сопротивление, тем больший ток он способен ограничить, тем больше тепла он выделяет, тем больше напряжения падает на нем.

Закон Ома для электрической цепи

Основной закон всего электричества. Связывает между собой Напряжение(V), Силу тока(I) и Сопротивление(R).

Интерпретировать эти символы на человеческий язык можно по-разному. Главное — уметь применить для каждой конкретной цепи. Давайте используем Закон Ома для нашей цепи с резистором и лампочкой, рассмотренной выше, и рассчитаем сопротивление резистора, при котором ток от источника питания на 12В ограничится до 0,2. При этом считаем сопротивление лампочки равным 0.

V=I*R => R=V/I => R= 12В / 0,2А => R=60Ом

Итак. Если встроить в цепь с источником питания и лампочкой, сопротивление которой равно 0, резистор номиналом 60 Ом, тогда ток, протекающий по цепи, будет составлять 0,2А.

Характеристика мощности резистора

Микропрогер, знай и помни! Параметр мощности резистора является одним из наиболее важных при построении схем для реальных устройств.

Мощность электрического тока на каком-либо участке цепи равна произведению силы тока, протекающую по этому участку на напряжение на этом участке цепи. P=I*U. Единица измерения 1Вт.

При протекании тока через резистор совершается работа по ограничению электрического тока. При совершении работы выделяется тепло. Резистор рассеивает это тепло в окружающую среду. Но если резистор будет совершать слишком большую работу, выделять слишком много тепла — он перестанет успевать рассеивать вырабатывающееся внутри него тепло, очень сильно нагреется и сгорит. Что произойдет в результате этого казуса, зависит от твоего личного коэффициента удачи.

Характеристика мощности резистора — это максимальная мощность тока, которую он способен выдержать и не перегреться.

Расчет мощности резистора

Рассчитаем мощность резистора для нашей цепи с лампочкой. Итак. Имеем ток, проходящий по цепи(а значит и через резистор), равный 0,2А.

Падение напряжения на резисторе равно 5В (не 12В, не 7В, а именно 5 — те самые 5, которые вольтметр показывает на резисторе). Это значит, что мощностьтока через резистор равна P=I*V=0,2А*5В=1Вт.

Делаем вывод: резистор для нашей цепи должен иметь максимальную мощность не менее(а лучше более) 1Вт. Иначе он перегреется и выйдет из строя.

Соединение резисторов

Резисторы в цепях электрического тока имеют последовательное и параллельное соединение.

При последовательном соединении общее сопротивление резисторов является суммой сопротивлений каждого резистора в соединении:

При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:

Источники

https://math-nttt.ru/teoriya/raschet-padeniya-napryazheniya-na-rezistore.html
https://ugstroialyans.ru/podbor-rezistora-dlya-ponizheniya-napryazheniya/
https://strop-snab.ru/teoriya/ponizhenie-napryazheniya-rezistorom.html
https://1000eletric.com/kak-rasschitat-padenie-napryazheniya-na-rezistore/

Как вам статья?

Павел

Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники

Написать

Пишите свои рекомендации и задавайте вопросы

Источник

Резистор в цепи переменного тока

Катушка в цепи переменного тока

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Условие квазистационарности

Резистор в цепи переменного тока

Конденсатор в цепи переменного тока

Катушка в цепи переменного тока

Теги:

Что такое падение напряжения на резисторе

Физическое определение

Значение сопротивления

Импеданс резистора

Характеристика мощности резистора

Схема делителя напряжения на резисторах

Как рассчитать сопротивление для понижения напряжения: формула падения на резисторе

Значение сопротивления

Импеданс резистора

Параллельное соединение

Последовательное включение

Расчёт делителя напряжения

Определение силы тока на резисторе при разных типах соединения

Как понизить напряжение с помощью резистора

Подбор резистора для понижения напряжения

Какое напряжение после резистора

Пример с лампочкой

Единица измерения сопротивления резистора

Закон Ома для электрической цепи

Характеристика мощности резистора

Расчет мощности резистора

Соединение резисторов

Не пропустите также: