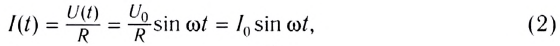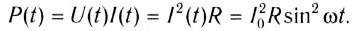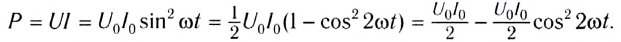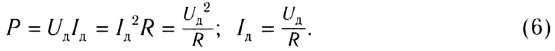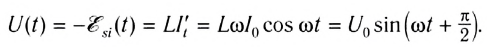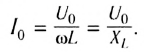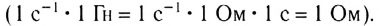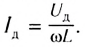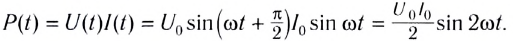Индуктивность
Время на прочтение
9 мин
Количество просмотров 19K
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.
Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Как хорошо сказано в wiki — “При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.”
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «
Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
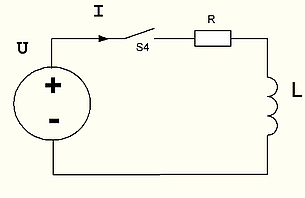
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
В водопроводной аналогии этому явлению можно сопоставить гидравлический удар, когда масса воды в водопроводе набирает скорость, и при резком закрытии крана вода, продолжая двигаться по инерции, создает высокое давление, что может привести к разрыву трубы.
Причины по которой индуктивность имеет такие свойства (поддержание тока в цепи) хорошо описаны в wiki —
https://ru.wikipedia.org/wiki/Самоиндукция
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
По отношению к конденсатору , основным отличием индуктивности, если говорить простыми словами, является то, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность наоборот — пропускает постоянный ток и не пропускает переменный.
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.
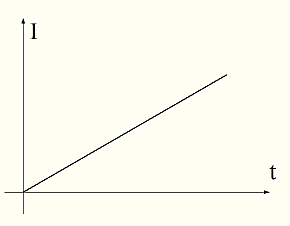
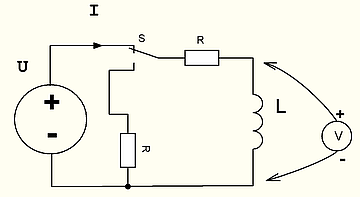
Рассмотрим цепь на рис. 13 — подключение катушки индуктивности к генератору напряжения.
Ниже представлен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.
При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?
Ну тут из серии «кто кого заборет — слон или кит».
Попробуйте проанализировать работу схемы (hint — вообще схема изображена с ошибкой. В чем она заключается? Как нарисовать схему правильно?)
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16
Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
В первый момент после замыкания ключа ток в цепи будет равен 0, так как индуктивность препятствует изменению тока. К вагонетке приложили силу, но в первый момент времени ее скорость равна 0. Затем ток начинает возрастать (вагонетка разгоняется). Пружина разжимается все больше и больше, скорость вагонетки (ток) растет и в какой-то момент времени пружина оказывается не сжата. Конденсатор разрядился до 0. Но. Мы помним что «ток в индуктивности мгновенно остановить нельзя!» Вагонетка разогналась и даже если мы не будем ее толкать, она будет двигаться по инерции. То есть индуктивность будет поддерживать ток и при этом заряжать конденсатор, но уже в другой полярности — заряды теперь будут скапливаться на другой обкладке конденсатора. Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
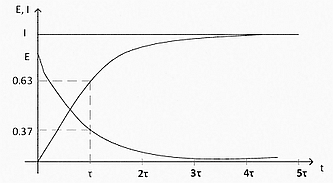
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.
На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
В этом случае процесс разворачивается следующим образом. При замыкании ключа S4 цепь замкнется и должен был бы пойти ток. Однако, катушка индуктивности препятствует изменению тока, и в первый момент времени после замыкания ключа ток останется равным 0! По сути дела катушка в этот момент представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке целиком. Можно и по другому подойти — Ur=I*R. Падение напряжения на резисторе равно I*R, I у нас равен 0, поэтому напряжение на резисторе тоже равно 0, и к катушке будет приложено полное напряжение U. Дальше ток в катушке будет расти. В области 0 линейно кстати (см рис 19 «Переход Суворова через Альпы» «Экспонента проходит через 0 под углом 45 градусов»). Ток будет расти и падение напряжения на резисторе тоже будет расти. А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.
зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения.»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени. Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.
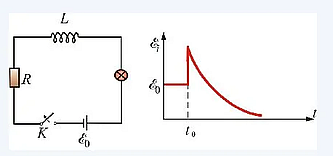
Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь
Вопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.
Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
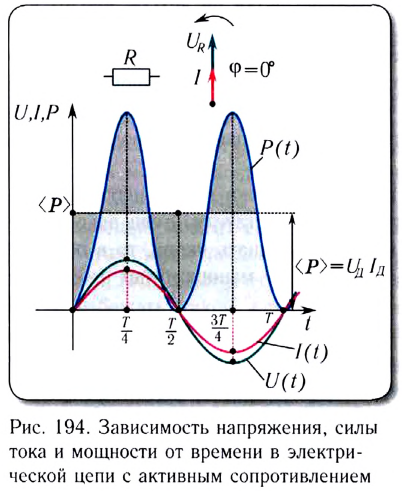
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где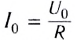 
— амплитудное значение силы тока в цепи.
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины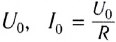 
называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность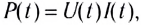 
которая, в отличие от цепей постоянного тока, изменяется с течением времени.
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока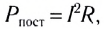 
то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока
Аналогично можно ввести действующее значение и для напряжения
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Катушка индуктивности в цепях переменного тока
Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток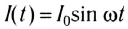 
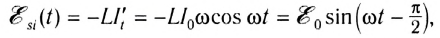
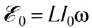
вызывает появление ЭДС самоиндукции:
где 
— амплитудное значение ЭДС самоиндукции (рис. 195).
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи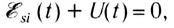 
где U(t) напряжение на концах катушки.
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде 
Величину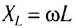 
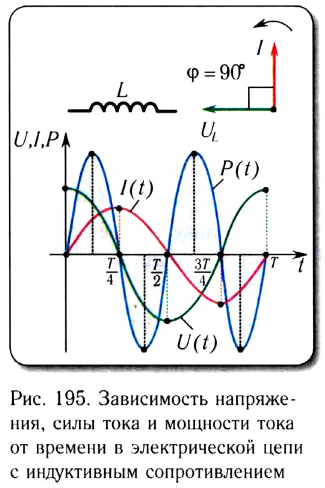
называют индуктивным сопротивлением катушки. Оно пропорционально индуктивности катушки и частоте переменного тока в цепи 
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на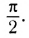 
Такой сдвиг фаз между колебаниями силы тока и напряжения характерен в целом для цепей переменного тока, содержащих элементы, обладающие индуктивностью.
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока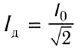 
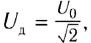
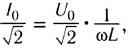
и напряжения 
так как 
тогда 
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
Поскольку среднее за период значение функции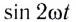 
равно нулю, то и средняя мощность за период также равна нулю:
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля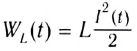 
в катушке, а в течение второй и четвертой — в режиме генератора, возвращая источнику запасенную энергию.
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Переменный электрический ток
Что такое катушка индуктивности
Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В — магнитное поле, Вб
I — сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I — сила тока в катушке , А
U — напряжение в катушке, В
R — сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
[quads id=1]
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 — это каркас катушки
2 — это витки катушки
3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
[quads id=1]
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке: