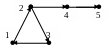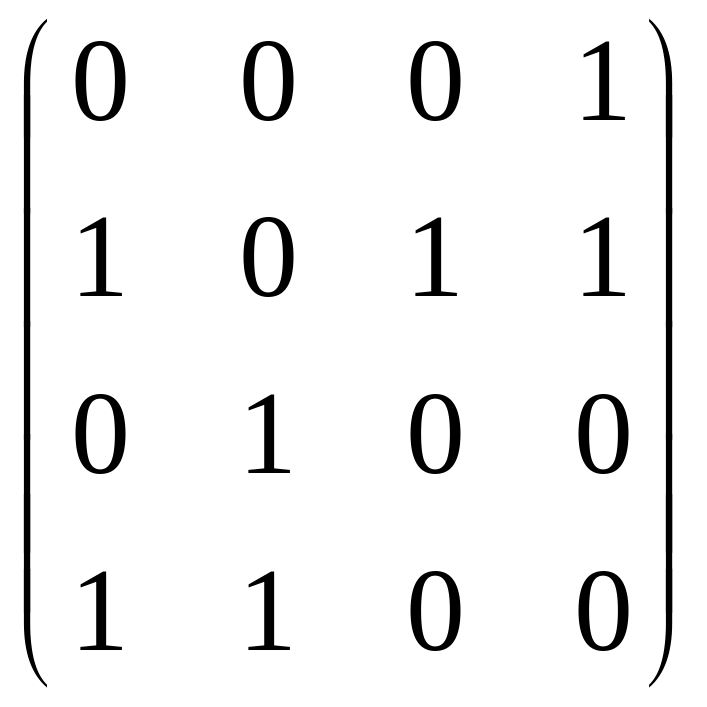Как найти направление графа

Теория графов. Термины и определения в картинках

В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.

Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов. 

Граф — это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.

Например, граф на рисунке состоит из 8 вершин и 8 рёбер.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними — за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.

В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус  “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов. 

Вершина — точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.

Ребро — неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге — не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.

Инцидентность — вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру. 

Смежность вершин — две вершины называются смежными, если они инцидентны одному ребру.

Смежность рёбер — два ребра называются смежными, если они инцедентны одной вершине.

Говоря проще — две вершины смежные, если они соединены ребром, два ребра смежные — если они соединены вершиной.

Петля — ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине. 

Псевдограф — граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название. 

Кратные рёбра — рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.

Мультиграф — граф с кратными рёбрами.

Псевдомультиграф — граф с петлями и кратными рёбрами.

Степень вершины — это количество рёбер, инцидентных указанной вершине. По-другому — количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.

Изолированная вершина — вершина с нулевой степенью.

Висячая вершина — вершина со степенью 1.

Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа. 

Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.

Полный граф — это граф, в котором каждые две вершины соединены одним ребром. 

Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N — каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N — 1) / 2.

Регулярный граф — граф, в котором степени всех вершин одинаковые.

Двудольный граф — если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.

Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.

Если это невозможно сделать, то граф называется “непланарным”.

Минимальные непланарные графы — это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.

Путь или Маршрут — это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.

Длина пути — количество рёбер в пути.

Цепь — маршрут без повторяющихся рёбер.

Простая цепь — цепь без повторяющихся вершин.

Цикл или Контур — цепь, в котором последняя вершина совпадает с первой. 

Длина цикла — количество рёбер в цикле.

Самый короткий цикл — это петля.

Цикл Эйлера — цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.

Цикл Гамильтона — цикл, проходящий через все вершины графа по одному разу. Другими словами — это простой цикл, в который входят все вершины графа.

Взвешенный граф — граф, в котором у каждого ребра и/или каждой вершины есть “вес” — некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути. 

Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса — “Алгоритмы и структуры данных”.

Связный граф — граф, в котором существует путь между любыми двумия вершинами.

Дерево — связный граф без циклов.

Между любыми двумя вершинами дерева существует единственный путь.

Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.

Лес — граф, в котором несколько деревьев.

Ориентированный граф или Орграф — граф, в котором рёбра имеют направления.

Дуга — направленные рёбра в ориентированном графе.

Полустепень захода вершины — количество дуг, заходящих в эту вершину.

Исток — вершина с нулевой полустепенью захода.

Полустепень исхода вершины — количество дуг, исходящих из этой вершины

Сток — вершина с нулевой полустепенью исхода.

Компонента связности — множество таких вершин графа, что между любыми двумя вершинами существует маршрут.

Компонента сильной связности — максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.

Компонента слабой связности — максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).

Мост — ребро, при удалении которого, количество связанных компонент графа увеличивается.

Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи — дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.

• Узнать о курсе подробнее

• Записаться на интенсив: «Алгоритм сжатия данных — код Хаффмана. Создание Архиватора.». День 1

• Записаться на интенсив: «Алгоритм сжатия данных — код Хаффмана. Создание Архиватора.». День 2

Введение

Граф носит название взвешенного, кода каждое ребро имеет свой вес, то есть ему поставлено в соответствие числовое значение. Невозможно, чтобы два ребра соединяли одни и те же точки.

Существует много алгоритмов нахождения минимального пути внутри взвешенного связного графа. Самым коротким путём между двумя вершинами графа будет маршрут по рёбрам, при котором суммарный вес рёбер будет минимальным. В качестве примера практического применения графов можно привести вариант, когда нужно переехать из одного города в другой по кратчайшему пути. Существует несколько дорог между городами и каждая имеет свою длину.

На языке графов это задача о самом коротком маршруте, то есть поиске кратчайшего маршрута между точками графа или минимизация суммарного весового показателя рёбер, из которых состоит маршрут. Задача о самом коротком маршруте считается самой важной основополагающей задачей теории графов. В исходном (старом варианте) она звучит как задача о дилижансе. Важность этой задачи видна из её разных практических реализаций. К примеру, в навигаторах, работающих на основе GPS, выполняется нахождение маршрута минимальной длины между двумя перекрёстками. Вершинами графа в этом случае считаются перекрёстки, а рёбрами будут дороги, соединяющие перекрёстки. Когда суммарная длина пути между перекрёстками станет самой маленькой, то это значит, что найден оптимальный путь движения.

Постановка задачи поиска минимального пути

Проблема нахождения самого короткого пути на графе существует для случаев ориентированного, неориентированного и смешанного графов. Рассмотрим постановку задачи в наиболее простом варианте для неориентированного графа. При рассмотрении случая ориентированного или смешанного графа, необходимо ещё учесть в каких направлениях расположены рёбра графа.

Маршрут или путь внутри неориентированного графа является последовательным набором вершин (точек). Существует функция веса, отображающая рёбра с их весами, и неориентированный граф. Тогда минимальным путём из одной вершины в другую будет считаться путь, имеющий минимальную сумму. В случае, когда у всех рёбер одинаковый вес, тогда целью становится минимизация числа рёбер, которые надо пройти по маршруту.

Задача определения минимального пути может быть поставлена в следующих вариантах:

1. Нахождение кратчайшего маршрута к заданному пункту назначения. Необходимо сформировать самый короткий путь к пункту назначения, вершине t. Начало пути может быть в любой из вершин графа, кроме t. Если изменить направление всех рёбер графа, то задача сводится к задаче о единой начальной точке и в ней надо найти минимальный путь из исходной точки во все остальные.
2. Нахождение минимального маршрута между определённой парой точек. То есть необходимо определить самый короткий путь из точки U в точку V.
3. Нахождение минимального маршрута между всеми парами вершин. То есть надо определить самый короткий путь из каждой точки U в каждую точку V. Такую задачу возможно разрешить при помощи алгоритма, который предназначен для задачи с одной начальной точкой, но есть возможность решить её быстрее.

В разных постановочных вариантах, в качестве веса ребра могут фигурировать не только меры длины, но и цена, временные интервалы, ресурсы и так далее. Или иные параметры, которые могут быть связаны с преодолением всех рёбер пути. Это означает, что задача может быть использована в самых разных научных сферах (информатике, экономике, географии и других). Но бывают случаи, когда при решении задачи о минимальном маршруте, требуется учесть различные ограничивающие факторы.

При их учёте, есть вероятность существенного усложнения задачи, например:

1. Требуется найти самый короткий маршрут, который проходит через заданные точки. Здесь возможно сформулировать такие ограничивающие факторы: самый короткий путь должен пройти через выделенные точки, и самый короткий путь содержит минимальное число невыделенных точек.
2. Требуется найти самый короткий маршрут, но при минимальном покрытии точек ориентированного графа путями.
3. Необходимо определить самое маленькое по мощности количество путей.
4. Необходимо найти минимальное по количеству маршрутов подмножество всех маршрутов, но при этом каждая дуга должна принадлежать хотя бы одному из них.

Алгоритмы поиска путей в графе

Так как есть много разных постановок этой задачи, то, соответственно, существуют различные алгоритмы нахождения самого короткого маршрута на графе:

• Согласно алгоритму Дейкстры возможно найти самый короткий маршрут из одной точки на графе ко всем остальным точкам. Этот алгоритм справедлив лишь для графов, которые не имеют рёбер с отрицательным весом.
• Используя алгоритм Беллмана – Форда можно определить самый короткий маршрут от одной точки графа ко всем другим точкам во взвешенном графе. В данном случае рёбра могут иметь отрицательный вес.
• Алгоритм поиска по определению маршрута с минимальной ценой перемещения от одной точки (исходной) к конечной. Применяется поисковый алгоритм по первому самому лучшему совпадению на графе.
• Применение алгоритма Флойда — Уоршелла позволяет найти самый короткий маршрут между всеми точками взвешенного ориентированного графа.
• Использование алгоритма Джонсона позволяет найти самый короткий маршрут между всеми парами точек взвешенного ориентированного графа.
• Волновой алгоритм Ли базируется на способе выполнения поисковых операций в ширину. Определяется путь между точками графа, который содержит минимум промежуточных точек или рёбер.

3.1. Понятие маршрута

Маршрутом в
графе G=(V,E) называется чередующаяся
последовательность вершин и ребер (дуг)
– v₁, e₁, v₂,
e₂, …., v_n, e_n,v_n+1,
в которой любые два соседних элемента
инциденты.

Маршрут,
соединяющий вершины v₁ и v_n+1
можно также задать последовательностью
из одних вершин v₁, v₂,
v₃,…,v_n, v_n+1
или последовательностью ребер e₁,
e₂,…,e_n. Число n
ребер (или дуг) в маршруте называется
его длиной. Маршрут называется
циклическим, если v₁=v_n+1.

Маршруты в неориентированных графах

Маршрут в неорграфе
называется цепью, если все его ребра
различны. Цепь называется простой,
если все её вершины, кроме возможно
первой и последней, различны. Циклическая
цепь называется циклом, а простая
циклическая цепь – простым циклом.

Неорграф
без циклов называется ациклическим
графом.
Минимальная из длин циклов неорграфа
называется его обхватом.

Пример
1: Рассмотрим неорграф

Рис.
9

В данном примере
наборы вершин: (1,2); (1,2,4,7) являются простыми
цепями,: (1,2,4,7,8,4) — непростая цепь,
(1,2,4,7,8,4,2) – маршрут, который не является
цепью, (1,2,4,8,4,1) – непростой цикл, (1,2,4,1)
– простой цикл. Обхват графа равен 3.

Маршруты в ориентированных графах

Маршрут
ориентированного графа называется
путем, если все его дуги различны.

Путь
называется контуром, если v₁=v_n+1.
Граф не имеющий контуров называется
безконтурным. Вершина v
называется достижимой
из вершины u,
если существует путь из u
в v.

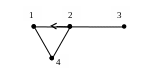
Пример 2: Рассмотрим
ориентированный граф

Рис. 10

В данном примере
наборы вершин (1,2,3,1) образуют контур.
Заметим, что здесь вершина 5 – достигается
из любой другой вершины, а из вершины 5
не достигается ни одна из остальных
вершин.

3.2. Связность в графах.

Неорграф
называется связным,
если любые две его несовпадающие вершины
соединены маршрутом. Граф называется
связным,
если соответствующий ему неорграф
является связным. В данном случае
соответствующий неориентированный
граф получается из исходного графа
путём замены всех его дуг рёбрами. Граф
называется сильно
связным,
если для каждой пары различных вершин
u
и v
существуют маршруты (u,v)
и (v,u).
Из этого определения следует, что любой
связный неорграф является также сильно
связным.
Понятии связности и сильной связности
распространяются также и на мультиграфы.

Отметим,
что граф в примере 1 является сильно
связным, а в приме2 – не сильно связный
граф.

Пример
3.
На следующем рисунке показан несвязный
граф.

Р

ис.
11

Всякий
максимальный по включению сильно связный
подграф данного графа называется его
сильно связной
компонентой,
или сильной
компонентой связности.

В примере 3 граф имеет две сильно связных компоненты.

3.3. Связность и матрица смежности графа

Теорема
1. Любой граф
представляется в виде объединения
непересекающихся (сильно) связных
компонент. Разложение графа на (сильно)
связные компоненты определяется
однозначно.

Таким
образом, множество вершин связных
компонент, а также сильных компонент
образуют разбиение множества вершин
графа, причем число с(G)
связных компонент графа G
определяется однозначно.

Теорема
2. Если A
матрица смежности графа G,
то (i,
j)
элемент матрицы A^k=A·A·A·_·…·A
(k
раз), есть число (v_i,
v_j)
маршрутов длины k.

Следствие
1. В графе G
мощности n
тогда и только тогда существует маршрут
(v_i,
v_j)
, причем v_i
≠v_j
, когда (i,
j)
– элемент матрицы A+A²+
A³+
A⁴+…+
A^n-1
не равен нулю.

Следствие
2. В графе G
мощности n
тогда и только тогда существует цикл,
содержащий вершину v_i
когда (i,
i)
– элемент матрицы A+A²+
A³+
A⁴+…+
A^n-1+Aⁿ
не равен нулю.

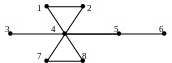
Пример.
При помощи матрицы смежности определим
существование всевозможных (1, 3) —
маршрутов в графе, изо браженном на
рисунке.

Рис.
12

П

о
графу находим матрицу смежности A:

A=
.

Её
элемент (1,3)=0, следовательно. (1, 3) маршрутов
длины 1 в графе нет. Затем находим:

A²=
*
=
.

В
этой матрице элемент (1,3)=0, т.е. (1, 3)
маршрута длины 2 в графе нет. Далее

A³=
A²·A
=
·
=

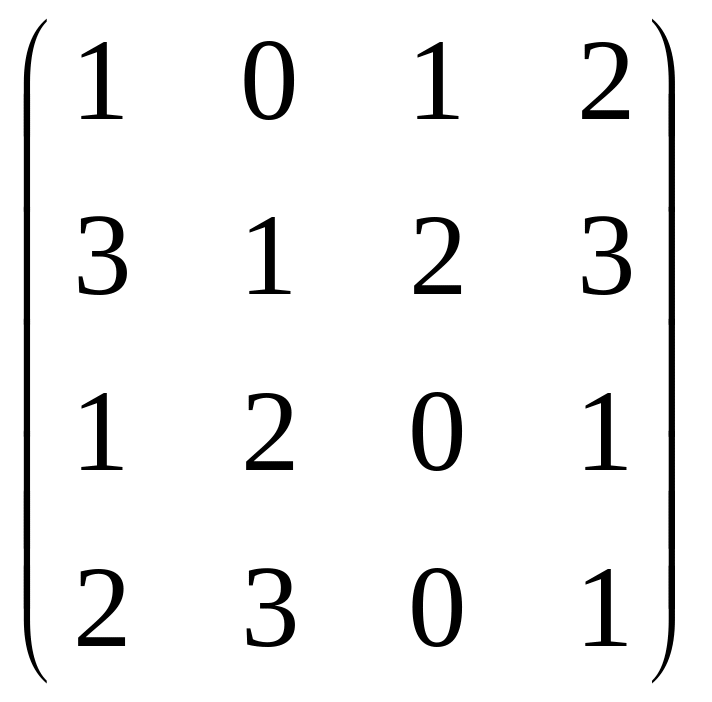
Eё
элемент (1, 3)=1, т.е. существует ровно один
(1, 3) — маршрут длины 3. Этот маршрут
определяется набором вершин (1, 4, 2, 3)

Эту
последовательность вершин можно найти
на основе перемножения матрицы смежности:
Элемент (1, 3) матрицы A³
получается при перемножении элемента
(1, 2) матрицы A²
на элемент (2, 3) матрицы A.
В свою очередь элемент (1, 2) матрицы A²
образуется при перемножении элемента
(1, 4) матрицы A
на элемент (4, 2) матрицы A,
т.е. следовательно, двигаясь от 1 к 3 за
3 шага, получаем маршрут (1,4, 2, 3).

В матрице
A³
элемент (4, 2) равен 3, это значит, что
существуют три (4,2) маршрута длины 3 : (4,
1, 4, 2), (4, 2, 4, 2), (4, 2, 3, 2).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

У взвешенных графов есть ребра, которым присвоены весы — некоторые числа. Например, они могут отражать стоимость перевозки груза, расстояние, которое нужно преодолеть. Это данные, с которыми нам нужно проводить различные действия. Пример взвешенных графов:

Взвешенные графы бывают и направленными, и неориентированными. В примере выше неориентированный взвешенный граф. Стоимость или расстояние от зеленого узла до оранжевого и наоборот равна трем. Допустим, вы хотите проехать между двумя городами — зеленым и оранжевым. Значит, вам предстоит проехать три мили.

Эти метрики определяются самостоятельно и могут быть изменены в зависимости от ситуации. Предположим, вам нужно попасть в розовый город из зеленого. Если посмотреть на граф города, мы не найдем прямых дорог или ребер между этими двумя городами. Поэтому мы можем поехать через другой город.

Наиболее перспективными будут маршруты из зеленого в розовый через оранжевый и синий. Если весами являются затраты между городами, то нам придется потратить 11 долларов на поездку через синий город, чтобы добраться до розового. Если мы воспользуемся другим маршрутом через оранжевый город, то нам придется заплатить за поездку всего десять долларов.

Каждое ребро может иметь несколько весовых коэффициентов — расстояние, время в пути или денежные затраты. Такие взвешенные графы обычно используются для программирования GPS и поисковых систем планирования путешествий, которые сравнивают время и стоимость перелета.

Типы графов можно определять по признакам, которые мы разобрали в этом уроке. Например, если вы увидите направление от одного узла к другому — это диграфы. Если у них еще есть ребра с числами — это направленные взвешенные графы. Когда вы научитесь определять тип графов, то сможете правильно решать задачи.