Как найти направление эдс индукции

Индуктированная электродвижущая сила (ЭДС) возникает в следующих случаях:

1. Когда движущийся проводник пересекает неподвижное магнитное поле или, наоборот, перемещающееся магнитное поле пересекает неподвижный проводник; или когда проводник и магнитное поле, двигаясь в пространстве, перемещаются один относительно другого;
2. Когда переменное магнитное поле одного проводника, действуя на другой проводник, индуктирует в нем ЭДС (взаимоиндукция);
3. Когда изменяющееся магнитное поле индуктирует в енм самом ЭДС (самоиндукция).

Таким образом, всякое изменение во времени величины магнитного потока, пронизывающего замкнутый контур (виток, рамку), сопровождается появлением в проводнике индуктированной ЭДС.

Как было отмечено в статье «Явление электромагнитной индукции», направление ЭДС магнитной индукции зависит от направления движения проводника и от направления магнитного поля.

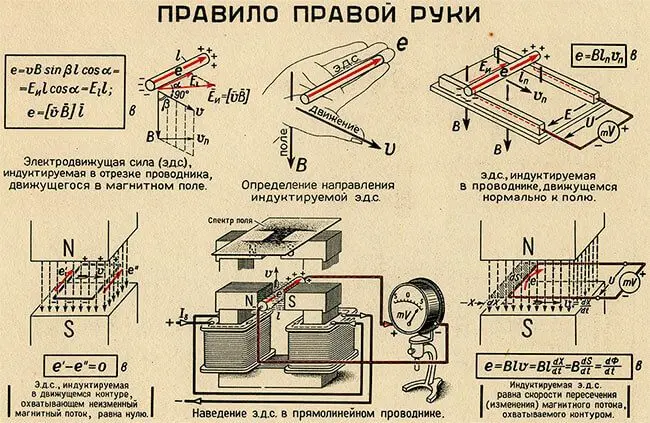
Для определения направления индуктированной ЭДС в проводнике служит «правило правой руки». Оно заключается в следующем: если мысленно расположить правую руку в магнитном поле вдоль проводника так, чтобы магнитные линии, выходящие из северного полюса, входили в ладонь, а большой отогнутый палец совпадал с направлением движения проводника, то четыре вытянутых пальца будут указывать направление индуктированной ЭДС в проводнике (рисунок 1).

Рисунок 1. Определение направления ЭДС индукции в проводнике по «правилу правой руки»

В случаях, когда проводник остается неподвижным, а магнитное поле движется, для определения направления индуктированной ЭДС нужно предположить, что поле остается неподвижным, а проводник движется в сторону, обратную движению поля, и применить «правило правой руки».

Рисунок 2. Электромагнитная индукция в проводнике

Явление индуктированной ЭДС можно также объяснить при помощи электронной теории.

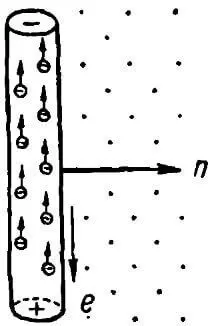
Поместим проводник в магнитное поле. Свободные электроны проводника будут находиться в беспорядочном тепловом движении. Положительные и отрицательные заряды равномерно расположены по всему объему проводника и взаимно нейтрализуют друг друга. Будем перемещать проводник с определенной скоростью в однородном магнитном поле в направлении n (рисунок 2) перпендикулярно вектору магнитной индукции. Магнитные линии, показанные точками, направлены из-за плоскости чертежа к читателю.

На электрические заряды проводника в этом случае будет действовать сила, под действием которой свободные электроны получат добавочную составляющую скорости и будут двигаться вдоль проводника.

В то время как положительные заряды, связанные с кристаллической решеткой проводника, относительно проводника не смещаются, движущиеся вместе с проводником свободные электроны могут перемещаться относительно него.

Рисунок 3. Разложение скорости движения проводника в магнитном поле

В нашем примере электроны движутся от нижнего края проводника к его верхнему краю, что соответствует направлению тока сверху вниз. Направление индуктированной ЭДС и тока в проводнике, как легко убедиться, согласуется с правилом правой руки.

Величина ЭДС индукции магнитного поля в проводнике зависит:

1. от величины индукции B магнитного поля, так как чем гуще расположены магнитные индукционные линии, тем больше число их пересечет проводник за единицу времени (секунду);
2. от скорости движения проводника v в магнитном поле, так как при большой скорости движения проводник может больше пересечь индукционных линий в секунду;
3. от рабочей (находящейся в магнитном поле) длины проводника l, так как длинный проводник может больше пересечь индукционных линий в секунду;
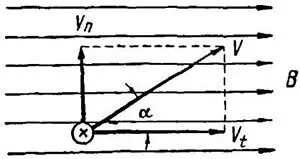
4. от величины синуса угла α между направлением движения проводника и направлением магнитного поля (рисунок 3).

Раскладываем вектор скорости движения проводника в магнитном поле на две составляющие: v_n – составляющую нормальную к направлению поля (v_n = v × sin α) и v_t – тангенциальную составляющую (v_t = v × cos α), которая не принимает участия в создании ЭДС, так как при движени под воздействием тангенциальной составляющей проводник двигался бы параллельно вектору B и не пересекал бы линии магнитной индукции.

Формула ЭДС индукции дает возможность определить ее величину:

e = B × l × v × sin α (В) .

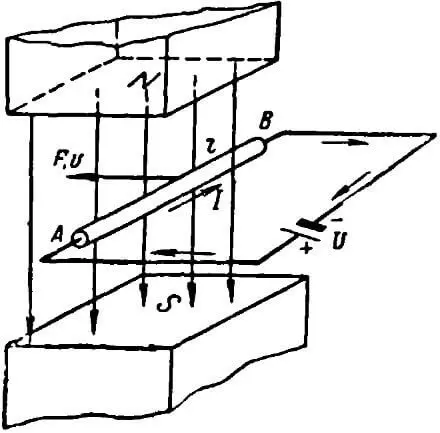
Познакомившись с явлением электромагнитной индукции, рассмотрим еще раз процесс преобразования электрической энергии в механическую.

Рисунок 4. Преобразование электрической энергии в механическую

Пусть прямолинейный проводник АВ (рисунок 4), по которому проходит ток от источника напряжения, помещен во внешнее магнитное поле. Если проводник неподвижен, то энергия источника напряжения расходуется исключительно на нагрев проводника:

A = U × I × t = I² × r × t (Дж) .

Затрачиваемая мощность будет равна:

P_эл = U × I = I² × r (Вт) ,

откуда определяем ток в цепи:

(1)

Однако нам известно, что проводник с током, помещенный в магнитное поле, будет испытывать силу со стороны поля, стремящуюся перемещать проводник в магнитном поле в направлении, определяемом правилом левой руки. При своем движении проводник будет пересекать магнитные силовые линии поля и в нем по закону электромагнитной индукции возникнет индуктированная ЭДС. Направление этой ЭДС, определенное по правилу правой руки, будет обратным току I. Назовем ее обратной ЭДС E_обр. Величина E_обр согласно закону электромагнитной индукции будет равна:

E_обр = B × l × v (В) .

По второму закону Кирхгофа для замкнутой цепи имеем:

U – E_обр = I × r

или

откуда ток в цепи

(3)

Сравнивая выражения (1) и (3), видим, что в проводнике, движущемся в магнитном поле, при одних и тех же значениях U и r ток будет меньше, чем при неподвижном проводнике.

Умножая полученное выражение (2) на I, получим:

U × I = E_обр × I +  I² × r .

Так как E_обр = B × l × v, то

U × I = B × l × v × I +  I² × r .

Учитывая, что B × l × I = F и F × v = P_мех, имеем:

U × I = F × v + I² × r

или

P = P_мех + P_эм .

Последнее выражение показывает, что при движении проводника с током в магнитном поле мощность источника напряжения преобразуется в тепловую и механическую мощности.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

Электромагнитная индукция

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.

Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.

Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?

Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.

1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».

Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.

При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.

Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.

При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.

Вывод.

Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.

Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.

Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.

Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.

Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).

2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.

Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.

3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.

Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.

Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.

Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».

к оглавлению ▴

Магнитный поток

Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.

Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией .

Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.

В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:

(1)

Теперь рассмотрим общий случай, когда вектор образует угол с нормалью к плоскости контура (рис. 2).

Рис. 2.

Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции (а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем . Но , поэтому

(2)

Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть ), то магнитный поток становится равным нулю.

А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.

Единицей измерения магнитного потока является вебер (Вб). Как видим,

Вб = Тл · м = В · с. (3)

Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как ). Но множители и как раз и образуют магнитный поток!

Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.

Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.

к оглавлению ▴

ЭДС индукции

Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.

Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается .

Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.

Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.

к оглавлению ▴

Закон электромагнитной индукции Фарадея

Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.

Если за малое время изменение магнитного потока равно , то скорость изменения магнитного потока — это дробь (или, что тоже самое, производная магнитного потока по времени).

Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:

Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.

Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:

(4)

ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:

(5)

Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.

Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.

к оглавлению ▴

Правило Ленца

Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.

Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.

Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.

Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.

Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .

Правило Ленца позволяет находить направление индукционного тока в любой ситуации.

Рассмотрим некоторые примеры применения правила Ленца.

Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.

Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.

Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает

Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает

Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.

В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.

к оглавлению ▴

Взаимодействие магнита с контуром

Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?

Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.

1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.

Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.

Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .

Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1

Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.

Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.

Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .

Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.

к оглавлению ▴

Закон Фарадея + Правило Ленца = Снятие модуля

Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.

Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.

Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным .

ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.

Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.

Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен: .

Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает

Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.

А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть, (рис. 6).

Рис. 6. Магнитный поток возрастает

Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :

(6)

Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.

к оглавлению ▴

Вихревое электрическое поле

Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?

Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.

Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.

Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.

Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля

Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля

Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.

Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.

1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.

Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .

Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость вихревого электрического поля одинакова во всех точках кольца. Работа силы , с которой вихревое поле действует на заряд , равна:

Следовательно, для ЭДС индукции получаем:

к оглавлению ▴

ЭДС индукции в движущемся проводнике

Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.

Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле . По рельсам движется тонкий проводящий стержень со скоростью ; он всё время остаётся перпендикулярным рельсам (рис. 9).

Рис. 9. Движение проводника в магнитном поле

Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью на заряд будет действовать сила Лоренца:

Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).

Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда от точки к точке наша сторонняя сила совершит работу:

(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:

(7)

Таким образом, стержень аналогичен источнику тока с положительной клеммой и отрицательной клеммой . Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке , отрицательные — к точке .

Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце будет возрастать кулоновская сила, с которой положительный свободный заряд отталкивается от и притягивается к — и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).

Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении (от «плюса источника» к «минусу» N). Предположим, что сопротивление стержня равно (это аналог внутреннего сопротивления источника тока), а сопротивление участка равно (сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:

Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень проходит путь и занимает положение (рис. 9). Площадь контура возрастает на величину площади прямоугольника :

Магнитный поток через контур увеличивается. Приращение магнитного потока равно:

Скорость изменения магнитного потока положительна и равна ЭДС индукции:

Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю и, стало быть, препятствует возрастанию магнитного потока через контур.

На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.

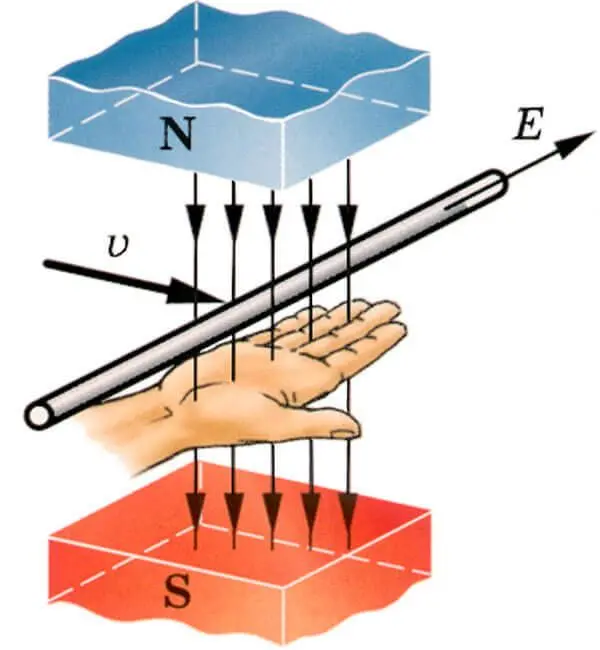
Величина и направление ЭДС индукции (в день науки)

Величина ЭДС
индукции зависит от количества силовых линий поля, пересекающих проводник в
единицу времени, т. е. от скорости движения проводника в поле.

Величина
индуктированной ЭДС находится в прямой зависимости от скорости движения
проводника в магнитном поле.

Величина
индуктированной ЭДС зависит также и от длины той части проводника, которая
пересекается силовыми линиями поля. Чем большая часть проводника пересекается
силовыми линиями поля, тем большая ЭДС индуктируется в проводнике. И, наконец,
чем сильнее магнитное поле, т. е. чем больше его индукция, тем большая ЭДС
возникает в проводнике, пересекающем это поле.

Итак, величина
ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо
пропорциональна индукции магнитного поля, длине проводника и скорости его
перемещения.

Зависимость
эта выражается формулой Е = Blv,

где Е — ЭДС
индукции; В — магнитная индукция; I — длина проводника; v — скорость движения
проводника.

Следует
твердо помнить, что в проводнике, перемещающемся в магнитном поле, ЭДС
индукции возникает только в том случае, если этот проводник пересекается
магнитными силовыми линиями поля. Если же проводник перемещается вдоль
силовых линий поля, т. е. не пересекает, а как бы скользит по ним, то никакой
ЭДС в нем не индуктируется. Поэтому приведенная выше формула справедлива только
в том случае, когда проводник перемещается перпендикулярно магнитным силовым
линиям поля.

Направление
индуктированной ЭДС (а также и тока в проводнике) зависит от того, в какую
сторону движется проводник. Для определения направления индуктированной ЭДС
существует правило правой руки.

Если держать
ладонь правой руки так, чтобы в нее входили магнитные силовые линии поля, а
отогнутый большой палец указывал бы направление движения проводника, то
вытянутые четыре пальца укажут направление действия индуктированной ЭДС и
направление тока в проводнике. 

Правило правой руки

Соседние файлы в папке РГР 2

• #
• #