Как найти наклон линии на графике

Загрузить PDF

Нахождение угла наклона прямой – это один из важнейших навыков в геометрии, необходимый для построения графика линейной функции или для определения координат точек пересечения прямой с осями X и Y. Угол наклона прямой определяет скорость ее роста или убывания,^[1] то есть как быстро прямая перемещается по вертикали в зависимости от движения по горизонтали. Угол наклона прямой легко вычисляется по координатам двух точек, лежащих на этой прямой.

1

Уясните формулу для вычисления углового коэффициента. Угловой коэффициент равен тангенсу угла наклона прямой, который она образует с осью Х, и вычисляется как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между двумя точками.
2

Выберите две точки и найдите их координаты. Можно выбрать любые две точки, лежащие на прямой.
3

Задайте порядок точек (относительно друг друга). Одна точка будет первой точкой, а другая – второй. Не имеет значения, какая точка будет первой, а какая второй – главное не перепутать их порядок в процессе вычисления.^[2]
4

Запишите формулу для вычисления углового коэффициента. Формула: ${frac {VR}{GR}}={frac {y_{{2}}-y_{{1}}}{x_{{2}}-x_{{1}}}}$ , где VR – вертикальное расстояние, определяемое изменением координаты «у», GR – горизонтальное расстояние, определяемое изменением координаты «х».^[3]

Реклама

1

В формулу для вычисления углового коэффициента подставьте координаты «у». Не перепутайте их с координатами «х» и убедитесь, что подставляете правильные координаты первой и второй точек.
2

В формулу для вычисления углового коэффициента подставьте координаты «х». Не перепутайте их с координатами «у» и убедитесь, что подставляете правильные координаты первой и второй точек.
3

Вычтите координаты «у». Вы найдете вертикальное расстояние.
4

Вычтите координаты «х». Вы найдете горизонтальное расстояние.
5

Если возможно, сократите дробь. Вы найдете угловой коэффициент.
6
Обращайте внимание на отрицательные числа. Угловой коэффициент может быть положительным или отрицательным. В случае положительного значения прямая возрастает (движется вверх слева направо); в случае отрицательного значения прямая убывает (движется вниз слева направо).
- Помните, что если и в числителе, и в знаменателе стоят отрицательные числа, то результат будет положительным.
- Если в числителе или в знаменателе стоит отрицательное число, то результат будет отрицательным.
7
Проверьте ответ. Для этого измерьте или посчитайте (по шкалам осей) вертикальное и горизонтальное расстояния. Если они совпали с вычисленными, то ответ правильный.
- Если измеренные или посчитанные вертикальное и горизонтальное расстояния не совпали с вычисленными, то ответ не правильный.
Реклама

Советы

Об этой статье

Эту страницу просматривали 90 508 раз.

Была ли эта статья полезной?

Источник

Download Article

The slope of a line is a measure of how fast it is changing. This can be for a straight line — where the slope tells you exactly how far up (positive slope) or down (negative slope) a line goes while it goes how far across. Slope can also be used for a line tangent to a curve. Or, it can be for a curved line when doing Calculus, where slope is also known as the «derivative» of a function. Either way, think of slope simply as the «rate of change» of a graph: if you make the variable «x» bigger, at what rate does «y» change? That is a way to see slope as a cause and an effect event.

1

Use slope to determine how steep, and in what direction (upward or downward), a line goes. Finding the slope of a line is easy, as long as you have or can setup a linear equation. This method works if and only if:^[1]
2

Find the number in front of the x, usually written as «m,» to determine slope. If your equation is already in the right form, , then simply pick the number in the «m» position (but if there is no number written in front of x then the slope is 1). That is your slope! Note that this number, m, is always multiplied by the variable, in this case an «x.» Check the following examples:

Advertisement
3

Reorganize the equation so one variable is isolated if the slope isn’t apparent. You can add, subtract, multiply, and more to isolate a variable, usually the «y.» Just remember that, whatever you do to one side of the equal sign (like add 3) you must do to the other side as well. Your final goal is an equation similar to . For example:

1
Use a graph and two points to find slope without the equation handy. If you’ve got a graph and a line, but no equation, you can still find the slope with ease. All you need are two points on the line, which you plug into the equation ${frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . While finding the slope, keep in mind the following information to help you check if you’re on the right track:^[5]
- Positive slopes go higher the further right you go.
- Negative slopes go lower the further right you go.
- Bigger slopes are steeper lines. Small slopes are always more gradual.
- Perfectly horizontal lines have a slope of zero.
- Perfectly vertical lines do not have a slope at all. Their slope is «undefined.»^[6]
2
Find two points, putting them in simple (x,y) form. Use the graph (or the test question) to find the x and y coordinates of two points on the graph. They can be any two points that the line crosses through. For an example, assume that the line in this method goes through (2,4) and (6,6).^[7]
- In each pair, the x coordinate is the first number, the y coordinate comes after the comma.
- Each x coordinate on a line has an associated y coordinate.
3
Label your points x₁, y₁, x₂, y₂, keeping each point with its pair. Continuing our first example, with the points (2,4) and (6,6), label the x and y coordinates of each point. You should end up with:^[8]
- x₁: 2
- y₁: 4
- x₂: 6
- y₂: 6^[9]
4

Plug your points into the «Point-Slope Formula» to get your slope. The following formula is used to find slope using any two points on a straight line: ${frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Simply plug in your four points and simplify:^[10]
5

Understand how the Point-Slope Formula works. The slope of a line is “Rise over Run:” how much the line goes up divided by how much the line «runs» to the right. The “rise” of the line is the difference between the y-values (remember, the Y-axis goes up and down), and the “run” of the line is the difference between the x-values (and the X-axis goes left and right).^[11]
6

Recognize other ways you may be tested to find slope. The equation of the slope is ${frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$ . This may also be shown using the Greek letter “Δ”, called “delta”, meaning “difference of”. Slope can also be shown as Δy/Δx, meaning «difference of y / difference of x:» this is the same exact question as «find the slope between

1
Review how to take a variety of derivatives from common functions. Derivatives give you the rate of change (or slope) at a single point on a line. The line can be curved or straight — it doesn’t matter. Think of it as how much the line is changing at any time, instead of the slope of the entire line. How you take derivatives changes depending on the type of function you have, so review how to take common derivatives before moving on.
- Review taking derivatives here
- The most simple derivatives, those for basic polynomial equations, are easy to find using a simple shortcut. This will be used for the rest of the method.
2

Understand what questions are asking for a slope using derivatives. You will not always be asked to explicitly find the derivative or slope of a curve. You might also be asked for the «rate of change at point (x,y). You could be asked for an equation for the slope of the graph, which simply means you need to take the derivative. Finally, you may be asked for «the slope of the tangent line at (x,y).» This, once again, just wants the slope of the curve at a specific point, (x,y).
3
Take the derivative of your function. You don’t even really need you graph, just the function or equation for your graph. For this example, use the function from earlier, $f(x)=2x^{2}+6x$ . Following the methods outlined here, take the derivative of this simple function.^[13]
- Derivative:
4

Plug in your point to the derivative equation to get your slope. The differential of a function will tell you the slope of the function at a given point. In other words, f’(x) is slope of the function at any point (x,f(x)) So, for the practice problem:
5
Check your point against a graph whenever possible. Know that not all points in calculus will have a slope. Calculus gets into complex equations and difficult graphs, and not all points will have a slope, or even exist on every graph. Whenever possible, use a graphing calculator to check the slope of your graph. If you can’t, draw the tangent line using your point and the slope (remember — «rise over run») and note if it looks like it could be correct.^[14]
- Tangent lines are just lines with the exact same slope as your point on the curve. To draw one, go up (positive) or down (negative) your slope (in the case of the example, 22 points up). Then move over one and draw a point. Connect the dots, (4,2) and (26,3) for your line.

Practice Problems and Answers

Our Most Loved Articles & Quizzes

Add New Question

Question

What is the slope for the equation y=1?

The graph of y=1 is a straight, horizontal line, meaning that it does not rise or fall as it moves left or right. Its slope is therefore zero.
Question

What if the equation is like x+y=0 or x-y=0?

That’s no problem. When x+y=0, y=-x. In this case the slope is -1. On the other hand, when x-y=0, y=x. Here the slope is +1.
Question

What’s the difference between a slope = 0 and slope = undefined?

A zero slope is a horizontal line (parallel to the x-axis), and an undefined slope is a vertical line (parallel to the y-axis).

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

About This Article

Article SummaryX

To find the slope of a linear equation, start by rearranging the given equation into slope-intercept form, which is y = mx + b. In slope-intercept form, «m» is the slope and «b» is the y-intercept. The slope of the line is whatever number is multiplied on the «x» variable, so just solve the equation for «x» to figure out the slope! For tips on finding the slope when you’re given two points on a graph, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 540,638 times.

Did this article help you?

Источник

Наклон графика — это не что иное, как уклон или крутизна линии. Эта статья дает полное представление о том, как найти наклон графика.

Когда график построен, он определяет отношения между любыми двумя физическими величинами, а наклон определяет некоторую другую третью физическую величину. Чтобы получить подробные сведения о том, как найти наклон графика, давайте прочитаем дальше.

График используется для визуального представления физических концепций для облегчения и лучшего понимания. Например, график движения используется для описания движения движущегося объекта, такого как положение, скорость, расстояние и ускорение. График помогает нам лучше понять взаимосвязь между двумя физическими концепциями. Например, график положения и времени позволяет нам узнать, как положение тела меняется со временем.

Компания декартов граф делится на четыре квадранта положительной и отрицательной осью x и положительной и отрицательной осью y. В первом квадранте x и y оба имеют положительные значения, тогда как в третьем квадранте оба становятся отрицательными. Теперь во втором и четвертом один положительный, а другой отрицательный.

После построения графика полученная линия или кривая называется наклоном. Наклон определяет значение некоторой конкретной физической величины. Например, наклон графика скорости и времени дает значение ускорения объекта.

Наклон графика рассчитывается по формуле:

Подставляя значения, формула становится:

Наклон = (y₂-y₁)/(Икс₂-x₁)

Как найти наклон четырех точек на графике

Оцениваем наклон заданных точек по формуле. Четыре точки можно расположить по-разному. Возьмем общий случай, показанный на рисунке выше. Здесь A (3, 5), B (-4, 4), C (-2, -1) и D (5, 1) — это четыре точки графика и, следовательно, четыре угла наклона. Значения наклона могут быть одинаковыми или разными. Итак, здесь мы индивидуально найдем наклон всех этих четырех наклонов, используя формулу:

Наклон = (y₂-y₁)/(Икс₂-x₁)

Наклон AB, подставляем значение A (3,5) и B (-4, 4)

Наклон AB=(4-5)/(-4-3)

Уклон АВ=1/7

Точно так же наклон BC становится:

Наклон ВС=(-1-4)/(-2+4)

Уклон ВС=-(5/2)

Наклон CD будет;

Наклон CD = (1+1)/(5+2)

Уклон CD=2/7

Наклон DA рассчитывается как;

Наклон DA=(1-5)/(5-3)

Наклон DA=-2

Как найти наклон графика с одной точкой

Если нам дан только один набор точек, мы не сможем найти наклон графика. Для наклона нужны две точки графика.

Эти два момента важны для описания линии; точно так же, как на рисунке (i), мы получаем определенную линию, построив график. По этим точкам можно оценить уклон. Но один набор точек может быть решением многих линий, и поэтому они могут иметь разные наклоны, как на рисунке (ii). И именно поэтому невозможно найти наклон графика по одной точке.

Мы можем найти наклон по одной точке, если нам также предоставят линию графика. Например, нам предоставлен приведенный выше график и точка A (2,4). Теперь в этом случае мы можем случайным образом взять другую точку B (4,6) на прямой и отследить ее координаты. Наконец, мы подставляем точки A и B в формулу наклона;

Наклон = (y₂-y₁)/(Икс₂-x₁)

Наклон = (6-4)/(4-2)

наклон=1

Таким образом, наклон графика равен 1.

Как найти наклон графика без точек

Если нам не дается ни одной точки, мы не можем найти наклон линии. Для расчета наклона должна быть какая-то информация. Таким образом, если точка не указана, то для того, чтобы найти наклон графика, нам необходимо предоставить уравнение прямой.

Прямая линия представлена уравнением в виде

у=мх+с

Здесь y — ордината, а x — абсцисса координаты. m дает значение наклона линии, а c — точка, в которой линия пересекает ось y.

Так что в случае, если нам предоставлено уравнение линии, мы можем найти по нему наклон. Например, уравнение задается как y = 4x + 2. Сравнивая его с вышеупомянутым общим уравнением, мы получаем:

м = 4.

Следовательно, наклон линии равен 4.

Как найти наклон прямой с двумя точками

Если нам не дано ничего, связанного с графиком, кроме двух точек, то мы также можем найти наклон линии. Он рассчитывается по общей формуле наклона. Предположим, нам предоставлены две точки, A (1,3) и B (2,6), и мы должны найти наклон от этих точек. Подставим значения этих точек в формулу наклона;

Наклон = (y₂-y₁)/(Икс₂-x₁)

Наклон = (6-3)/(2-1)

наклон=3

Следовательно, наклон линии становится равным 3.

Итак, в этой статье мы рассмотрели все, как найти уклон от одной точки, двух или четырех точек, и даже без какой-либо точки.

Часто задаваемые вопросы (FAQ)

Какую информацию предоставляет склон?

Наклон линии описывает наклон графика.

Глядя только на наклон, мы узнаем, изменяются ли эти две величины прямо или наоборот. Он определяет соотношение между двумя соответствующими физическими переменными. Вычисляя его, мы узнаем ценность некоторой третьей величины.

Как найти наклон графика?

Наклон линии оценивается, когда известны как минимум две точки графика.

Формула, которую мы используем для определения наклона прямой:

Здесь дельта x — это изменение по оси x, а дельта y — это изменение по оси y.

Поэтому формулу можно также сформулировать как:

Наклон = (y₂-y₁)/(Икс₂-x₁)

Можно ли найти уклон с помощью одной точки?

Если нам дана только одна точка и больше ничего, мы не сможем найти наклон линии.

С одной точки можно пройти множество линий, и поэтому могут быть разные уклоны. Следовательно, найти конкретный уклон от одной точки становится невозможным. Чтобы найти уклон, необходимо предоставить некоторую необходимую информацию.

Если набор точек не указан, какая еще информация должна быть доступна для определения наклона?

Без точки мы не можем найти наклон линии. Должна быть доступна какая-то другая информация.

Если точка не указана, то, по крайней мере, необходимо знать уравнение прямой, чтобы найти наклон прямой. Общее уравнение прямой: у = мх + с, где m — наклон линии.

Источник

Пользователям электронных таблиц часто требуется вычислить наклон линии, относящейся к данным в их электронной таблице. Если вы новый пользователь или привыкли использовать Microsoft Excel, может быть немного сложно понять, как это сделать самостоятельно. К счастью, поиск наклона в Google Sheets — это простой процесс, который занимает всего минуту или около того, если вы знаете, что делаете.

В этой статье вы научитесь рассчитывать значения уклона в Google Sheets с графиками и без них.

Что такое наклон?

Прежде всего, что такое наклон в Google Таблицах?

Наклон — это понятие в геометрии, которое описывает направление и крутизну линии на декартовой плоскости. (Декартова плоскость — это стандартная координатная сетка, которую вы, возможно, помните из уроков математики, с осью X и осью Y.)

Линия, идущая вверх слева направо на плоскости, имеет положительный наклон; линия, идущая вниз слева направо, имеет отрицательный наклон.

На диаграмме ниже синяя линия имеет положительный наклон, а красная линия имеет отрицательный наклон:

Наклон выражается в виде числа, и это число указывает, насколько линия поднимается или опускается на заданном расстоянии (известном как подъем над пробегом).

Вот пример:

Если линия идет от X=1, Y=0 до X=2, Y=1 (то есть линия поднимается на +1 по оси Y, а также поднимается на +1 по оси X), наклон равен 1. Если бы он увеличился с X = 1, Y = 0 до X = 2, Y = 2, наклон был бы равен 2 и так далее.

Большие числа означают более крутой наклон; наклон +10 означает линию, которая идет вверх на 10 по оси Y для каждой единицы, которую она перемещает по оси X, а наклон -10 означает линию, которая идет вниз на 10 по оси Y для каждой единицы на ось X.

В электронной таблице значения наклона обычно связаны с линейной регрессией, которая представляет собой способ анализа взаимосвязи между двумя или более переменными.

Переменные состоят из зависимых значений Y и независимых значений X, которые в электронных таблицах будут храниться как два отдельных столбца таблицы.

Зависимое значение — это значение, которое изменяется автоматически на количество, а независимое значение — это значение, которое может изменяться свободно. Типичным примером может быть один столбец (зависимая переменная X), который содержит ряд дат, а другой столбец (независимая переменная Y), содержащий числовые данные, например данные о продажах за этот месяц.

Где линии? Где график? Наклон зависит от того, как движется линия, верно?

Думайте о данных электронной таблицы как о точках графика. Данные, представленные в этой таблице, можно легко визуализировать с помощью линейного графика.

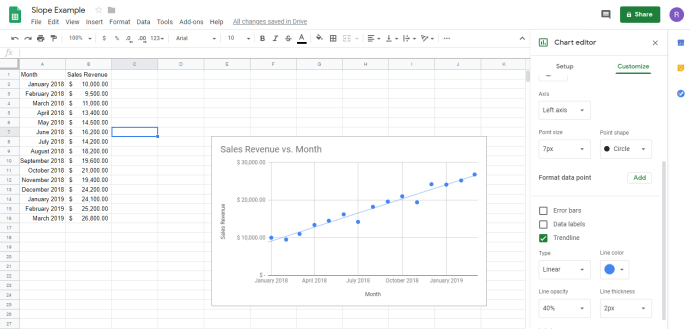
Google Sheets предоставляет простой, но мощный набор инструментов для создания линейных графиков из табличных данных. В этом примере все, что вам нужно сделать, это выбрать всю таблицу данных (от A1 до B16) и нажать кнопку «Вставить диаграмму». После этого Sheets мгновенно создаст следующую диаграмму:

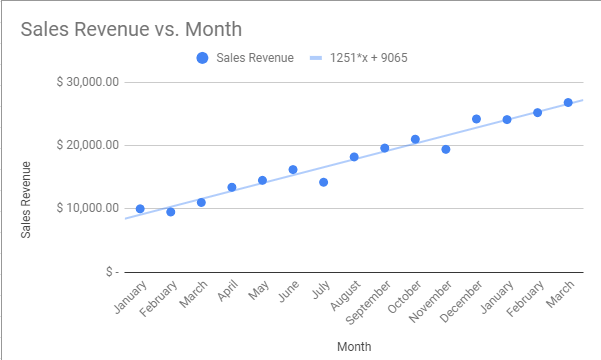
Откройте Google Таблицы и введите данные. Затем щелкните значок меню «Дополнительно» в правом верхнем углу.

Щелкните значок Диаграмма.

В одних местах падает, а в других поднимается! Как вы должны вычислить наклон такой сумасшедшей линии? Ответ — это то, что называется линией тренда. Линия тренда — это сглаженная версия вашей линии, которая показывает общую тенденцию чисел.

Щелкните Редактировать диаграмму. Получить линию тренда в Таблицах также легко.

Щелкните линию тренда. В появившемся редакторе диаграмм щелкните вкладку «Настройка», а затем измените тип диаграммы на Точечная диаграмма.

Перейдите на вкладку «Настройка», откройте раскрывающийся раздел «Серии» и переключите линию тренда.

Теперь ваша диаграмма должна выглядеть так:

Голубая линия, которая следует за цепочкой точек на графике, является линией тренда.

Так как же найти наклон этой линии?

Ну, если бы это был урок математики, тебе бы пришлось заняться математикой. К счастью, на дворе 21 век, и уроки математики остались далеко позади. Вместо этого мы можем просто сказать компьютеру сделать это за нас. Спасибо, Гугл.

Как найти наклон графика в Google Таблицах

Мы можем использовать Google Sheets для расчета наклона в редакторе диаграмм. Просто следуйте этим инструкциям, чтобы найти наклон любого линейного графика в Google Таблицах.

Выберите «Этикетка» > «Использовать формулу». Это добавит уравнение, которое Google Таблицы использовали для расчета линии тренда, а наклон нашей линии — это часть слева от члена *x.

В этом случае наклон равен +1251. Это означает, что за каждый прошедший месяц выручка от продаж увеличивается в общей сложности на 1251 доллар США.

3. Интересно, что на самом деле вам не обязательно иметь диаграмму, чтобы вычислить наклон. В Google Таблицах есть функция НАКЛОН, которая вычисляет наклон любой таблицы данных, не утруждая себя сначала отрисовкой ее в виде изображения. Однако рисование картинок очень помогает научиться делать все это, поэтому мы и сделали это именно так.

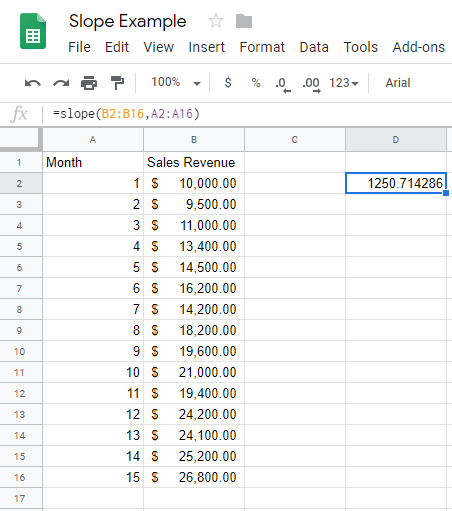
4. Вместо того, чтобы создавать диаграмму, вы можете просто добавить функцию НАКЛОН в ячейку электронной таблицы. Синтаксис функции НАКЛОН в Google Таблицах: НАКЛОН (данные_y, данные_x). Эта функция вернет то же значение наклона, что и в уравнении графика.

Обратите внимание, что порядок ввода немного отличается от того, как вы, вероятно, отображаете информацию в своей таблице. Это связано с тем, что Таблицы хотят, чтобы независимые данные (доход от продаж) помещались на первое место, а зависимая переменная (месяц) — на второе.

Вы также должны отметить, что функция НАКЛОН не так умна, как создатель диаграммы. Для зависимой переменной нужны чисто числовые данные, поэтому мы изменили эти ячейки на номера от 1 до 15.

Выберите любую пустую ячейку в электронной таблице, введите «= НАКЛОН (b2: b16, a2: a16)» и нажмите «Return».

А вот и наш наклон с чуть большей точностью, чем на графике.

Последние мысли

Вот как вы можете найти уклон в Google Таблицах. Надеюсь, если у вас возникли проблемы с самостоятельным пониманием этого, эти инструкции смогли вам помочь.

Если вы предпочитаете использовать Excel вместо Таблиц, есть также руководство TechJunkie по поиску значений уклона в Excel.

У вас есть интересные приложения для поиска уклона в Google Sheets? Поделитесь ими с нами ниже!

Источник

Что такое линейная функция и как выглядит ее график мы подробно разбирали здесь.

В этой статье мы остановимся на том, как находить коэффициент наклона прямой.

Как мы знаем, уравнение прямой имеет вид y=kx+b . В этом уравнении коэффициент при отвечает за наклон прямой и называется коэффициентом наклона. Он равен тангенсу угла между прямой и положительным направлением оси .

Внимание! Не просто между прямой и осью , а именно между прямой и положительным направлением оси .

Например, в прямой y=3x-1 коэффициент наклона равен , в прямой y=2-5x коэффициент наклона равен .

В уравнении прямой y=-1 слагаемое, содержащее отсутствует, следовательно, коэффициент при равен нулю. Угол наклона этой прямой к оси равен нулю — прямая y=-1 параллельна оси .

Если прямая наклонена вправо, то угол между прямой и положительным направлением оси — острый, соответственно, тангенс этого угла больше нуля, и коэффициент k>0 .

Например:

Здесь

Если прямая наклонена влево, то угол между прямой и положительным направлением оси — тупой, соответственно, тангенс этого угла меньше нуля, и коэффициент k<0 :

Здесь .

Решим две задачи на нахождение коэффициента наклона прямой.

1. Найдите угловой коэффициент прямой, проходящей через точки с координатами (-1;-1) и (1;3).

Решим эту задачу двумя способами.

А). Так как прямая проходит через точки (-1;-1) и (1;3), координаты этих точек удовлетворяют уравнению прямой y=kx+b . То есть если мы координаты каждой точки подставим в уравнение прямой, то получим верное равенство. Так как у нас две точки, получаем систему: