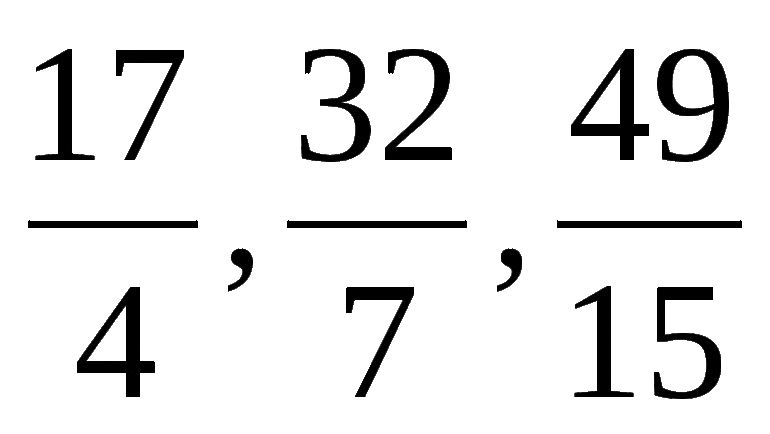Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 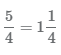
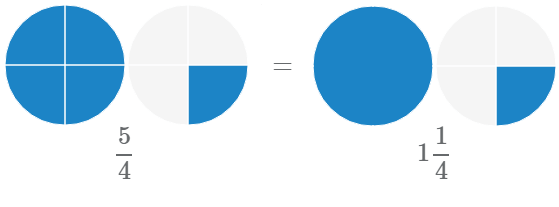
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 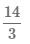
- 1 Разделим числитель на знаменатель 14 ÷ 3, в результате получим 4 целых и 2 в остатке.
- 2 Число 4 будет целой частью смешанного числа.
-
3 Остаток от деления 2 будет числителем дроби, а знаменатель останется прежним, равным 3. В результате получаем
Рассмотрим на примерах как переводить неправильные дроби в смешанные числа.
Пример Перевести неправильные дроби  в смешанные числа.
в смешанные числа.
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 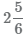
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
Пример Перевести смешанные числа  в неправильные дроби.
в неправильные дроби.
Как найти наибольшую и наименьшую дробь
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
Если мы до решаем эти дроби, то получим числа (frac<20> <4>= 5) и (frac<20> <10>= 2). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Сравните дроби с одинаковым числителем (frac<1><17>) и (frac<1><15>) .
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac<5> <10>).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac<3> <5>).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
Если у двух (или нескольких) дробей числитель одинаковый (то, что сверху черточки), то наименьшей дробью будет та, у которой знаменатель (то, что ниже черточки) наибольший, а наибольшей та, у которой знаменатель (то, что ниже черточки) наименьший.
В б наоборот — числители одинаковые, зато разные знаменатели. Представь себе пирог. Его разделили на столько частей, сколько написано внизу дроби. Из них взяли 31 часть. Чем на большее число частей поделили пирог, тем меньше часть (следовательно, находим где в знаменателе самое большое число — 53). Следовательно, пирог поделили на 53 части (маленькие) и из них взяли 31.
Ответы: 22/23 (самая большая в а)
31/53 (самая маленькая в б)
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры.
Количество источников, использованных в этой статье: 5. Вы найдете их список внизу страницы.
Сравнивают дроби обычно для того, чтобы узнать, какая больше, а какая меньше. Чтобы сравнить дроби, вам нужно привести их к одному знаменателю, тогда дробь с большим числителем большая, а с меньшим — меньшая. Самое сложное — это уяснить, как делать так, чтобы дроби имели одинаковые знаменатели, но все не так сложно, как кажется. Мы расскажем, как все это делать. Читайте дальше!
Правильные и неправильные дроби
- Правильные дроби
- Неправильные дроби
- Сравнение правильных и неправильных дробей
Обыкновенные дроби делятся на правильные и неправильные.
Правильные дроби
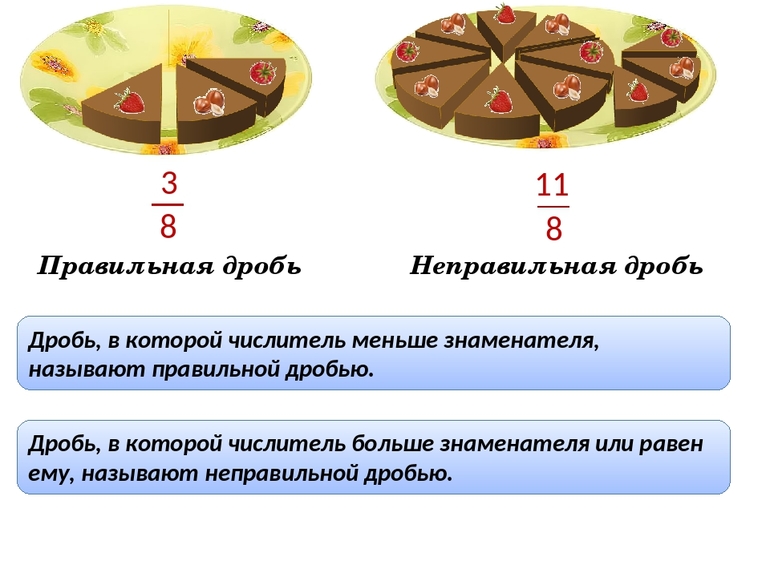
Правильная дробь — это обыкновенная дробь, у которой числитель меньше знаменателя.
Чтобы узнать является ли дробь правильной, надо сравнить её члены между собой. Члены дроби сравниваются в соответствии с правилом сравнения натуральных чисел.
Пример. Рассмотрим дробь:
у которой 7 — это числитель, а 8 — знаменатель. Сравним числитель со знаменателем:
7 < 8.
Так как числитель меньше знаменателя, значит данная дробь является правильной.
Любая правильная дробь меньше единицы:
Неправильные дроби
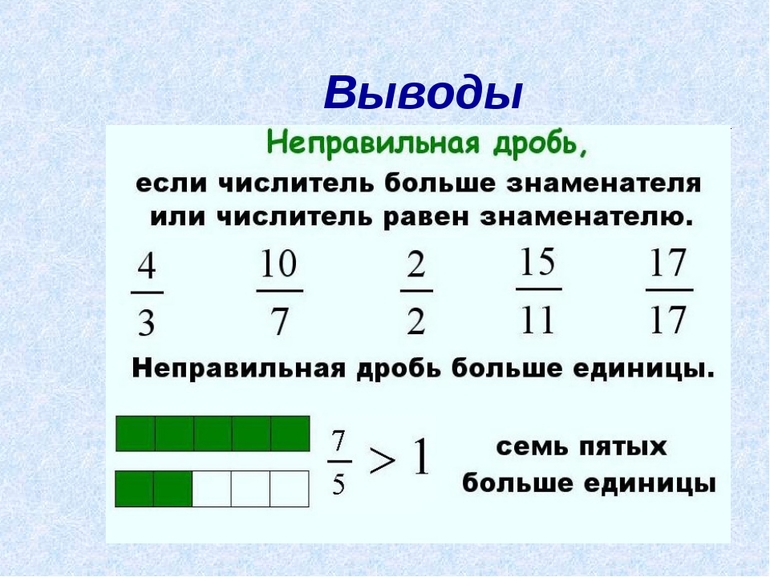
Неправильная дробь — это обыкновенная дробь, у которой числитель больше знаменателя или равен ему.
Пример 1. Рассмотрим дробь:
у которой 8 — это числитель, а 7 — знаменатель. Сравним числитель со знаменателем:
8 > 7.
Так как числитель больше знаменателя, значит данная дробь является неправильной.
Пример 2. Рассмотрим дробь:
Сравним числитель со знаменателем:
14 = 14.
Так как числитель равен знаменателю, значит данная дробь является неправильной.
Любая неправильная дробь больше единицы или равна ей:
Обратите внимание, что любое натуральное число можно представить в виде неправильной дроби, следующим образом:
Дробь с числителем p и знаменателем 1 – это другая форма записи натурального числа p: 
Число 0 принято считать равным дроби вида 
Любую неправильную дробь, у которой числитель больше знаменателя можно представить в виде смешанного числа.
Правила перевода и дополнительные примеры можно посмотреть в теме Перевод неправильной дроби в смешанное число
. Также для перевода неправильной дроби в смешанное число вы можете воспользоваться онлайн калькулятором.
Сравнение правильных и неправильных дробей
Любая неправильная обыкновенная дробь больше правильной, так как правильная дробь всегда меньше единицы, а неправильная больше единицы или равна ей.
Правила сравнения и дополнительные примеры можно посмотреть в теме Сравнение обыкновенных дробей
. Также для сравнения дробей или проверки сравнения вы можете воспользоваться онлайн калькулятором.
Неправильные дроби сравниваем по тем же правилам, что и обыкновенные дроби или правильные дроби. Рассмотрим подробно эти правила.
Сравнение неправильных дробей с одинаковыми знаменателями.
Есть несколько правил сравнения неправильных дробей с одинаковыми знаменателями:
- Если у неправильных дробей положительные числители, то та дробь больше у которой числитель больше.
- Если у неправильных дробей отрицательные числители, то та дробь больше у которой числитель меньше.
- Если у неправильных дробей разные знаки, то та дробь больше которая имеет знак “+”.
Рассмотрим пример:
Выполните сравнение неправильных дробей с одинаковыми знаменателями: а) (frac{20}{13}) и (frac{15}{13}) б) (frac{-161}{57}) и (frac{-98}{57}) г) (frac{17}{3}) и (frac{-11}{3})
Решение:
а) Раз у дробей (frac{20}{13}) и (frac{15}{13}) одинаковые знаменатели переходим к сравнению числителей 20>15,
(frac{20}{13}>frac{15}{13})
б) Так как знаменатели у дробей (frac{-161}{57}) и (frac{-98}{57}) одинаковые сравниваем отрицательные числители. Тот отрицательный числитель больше, который по модулю меньше.
|-161|=161
|-98|=98 меньше по модулю, значит это число ближе к нулю на числовой прямой чем -161, поэтому
-161<-98
(frac{-161}{57}<frac{-98}{57})
г) Сравнивать дроби с разными знаками (frac{17}{3}) и (frac{-11}{3}) очень просто, та дробь больше которая имеет знак “+”.
(frac{17}{3}>frac{-11}{3})
Сравнение неправильных дробей с одинаковыми числителями.
Запомнить:
- Если числители у неправильных дробей одинаковы и положительны, то та дробь больше у которой знаменатель меньше.
- Если у неправильной дроби числители отрицательные, то та дробь больше у которой знаменатель больше.
Пример:
Выполните сравнение неправильных дробей с одинаковыми числителями: а) (frac{21}{9}) и (frac{21}{10}) б) (frac{-15}{3}) и (frac{-15}{4})
Решение:
а) У неправильных дробей с одинаковыми положительными числителями (frac{21}{9}) и (frac{21}{10}), та дробь больше, где знаменатель меньше 9<10.
(frac{21}{9}>frac{21}{10})
б) У неправильных дробей с одинаковыми отрицательными числителями (frac{-15}{3}) и (frac{-15}{4}), та дробь больше где знаменатель больше 3<4.
(frac{-15}{3}<frac{-15}{4})
Сравнение неправильных дробей с разными знаменателями.
Правила сравнения неправильных дробей с разными знаменателями:
- Привести к общему знаменателю.
- Переходим к пункту сравнения неправильных дробей с одинаковыми знаменателями.
Рассмотрим пример:
Сравните неправильные дроби с разными знаменателями: а) (frac{15}{8}) и (frac{11}{6}) б) (frac{-103}{30}) и (frac{-43}{15}) г) (frac{47}{5}) и (frac{41}{5})
Решение:
а) Приведем дроби (frac{15}{8}) и (frac{11}{6}) к общему знаменателю. Общий знаменатель равен 24.
(begin{align}
&frac{15}{8}=frac{15 times 3}{8 times 3}=frac{45}{24} \\
&frac{11}{6}=frac{11 times 4}{6 times 4}=frac{44}{24} \\
end{align})
Сравниваем полученные числители 45>44, следовательно,
(begin{align}
&frac{45}{24}>frac{44}{24} \\
&frac{15}{8}>frac{11}{6} \\
end{align})
б) Найдем общий знаменатель для дробей (frac{-103}{30}) и (frac{-43}{15}) . Общий знаменатель равен 30.
(frac{-43}{15}=frac{-43 times 2}{15 times 2}=frac{-86}{30})
Сравниваем числители -103<-86
(begin{align}
&frac{-103}{30}<frac{-86}{30} \\
&frac{-103}{30}<frac{-43}{15} \\
end{align})
г) Сравниваем числители дробей (frac{47}{5}) и (frac{41}{5}), потому что знаменатель у дробей общий.
(frac{47}{5}>frac{41}{5})
Сравнение неправильной дроби с правильной дробью.
Правила сравнения неправильной дроби с правильной дробью:
- Если неправильная дробь положительна, то она всегда будет больше правильной положительной дроби.
- Если неправильная дробь отрицательна, то она всегда будет меньше правильной отрицательной дроби.
Пример:
Сравните правильную дробь и неправильную дробь: а) (frac{14}{13}) и (frac{13}{14}) б) (-frac{27}{6}) и (-frac{17}{18})
Решение:
а) Правильная и неправильная дробь положительны, поэтому неправильная дробь больше правильной дроби.
(frac{14}{13}>frac{13}{14})
б) Правильная и неправильная дробь отрицательны, поэтому неправильная дробь меньше правильной дроби.
(-frac{27}{6}<-frac{17}{18})
Сравнение неправильных дробей с нулем.
Правила сравнения неправильной дроби с нулем:
- Если неправильная дробь положительна, то она больше нуля.
- Если неправильная дробь отрицательна, то она меньше нуля.
Пример:
Сравните неправильную дробь с нулем: а) (frac{19}{7}) и 0 б) 0 и (-frac{4}{3})
Решение:
а) Неправильная дробь (frac{19}{7}) положительна, поэтому (frac{19}{7}>0)
б) Неправильная дробь (-frac{4}{3}) отрицательна, поэтому (0<-frac{4}{3})
Сравнение неправильных дробей с единицей.
Правила сравнения неправильной дроби с единицей:
- Если неправильная дробь положительна, то она больше или равна единице.
- Если неправильная дробь отрицательна, то она меньше или равна минус единице.
Пример:
Сравните неправильную дробь с единицей: а) (frac{10}{3}) и 1 б) -1 и (frac{-3}{3})
Решение:
а) Неправильная положительная дробь не равная единице всегда больше 1.
(frac{10}{3}>1)
б) Дробь (frac{-3}{3}= -1), поэтому
(-1=frac{-3}{3})
Равные неправильные дроби.
Правило равных неправильных дробей:
Неправильные дроби равны тогда, когда при одинаковых знаменателях равны их числители. Например:
(frac{-7}{4}=frac{-7}{4})
Общие сведения
Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.
В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.
Это легко проверить: 11/ 8 пиццы — это тоже что 8 / 8 плюс 3 / 8. То есть одна была полностью съедена, а с другой взяли только три кусочка. Так как отношение 8 / 8 — это целое (единица), то можно утверждать, что 8 / 8 = 1. Значит, произошедшее можно представить в виде равенства: 11 / 8 = 1 + 3 / 8.
Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:
- Правильные. Рациональные выражения, в которых числитель меньше или неравен делителю. Например, 1 / 16; 4 / 45; -78 / 123.
- Неправильные. Обыкновенные дроби, у которых знаменатель количественно меньше значения делимого или равен ему по численности. Например, 7 / 6; 19 / 19; 453 / 21.
- Смешанные. Отношения, включающие в свою запись как натуральное число, так и правильную дробь. Фактически они представляют собой их сумму: 4 (4 / 5) = 4 + 4 / 5
Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.
Так как, по сути, дроби — это числа, только чаще всего не целые, над ними можно выполнять любые операции. Для того чтобы школьника научить правильно решать дроби, в 5 классе, кроме теоретического материала несколько уроков уделяют практике. На ней, кроме непосредственного выполнения арифметических операций, учат преобразовывать дробные отношения из одного вида в другой.
Суть отношения
Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.
Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.
Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.
Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.
Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:
- натуральным числом — в случае когда числитель количественно совпадает со знаменателем;
- суммой правильной дроби и простого числа — если делимое не делится нацело на делитель.
Как и любое число, дробь может быть положительной и отрицательной. В первом случае она обозначает изменение чего-то в сторону увеличения, а во втором — уменьшения. Например, -6 / 5 может обозначать недостачу равную шесть пятых.
Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.
Превращение дробей
По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.
Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).
Поняв смысл такого перехода, можно выполнить превращение и в обратную сторону. Чтобы разобраться, как это сделать лучше, проще рассмотреть пример. Пусть имеется смешанное число 4 (5/8), его нужно превратить в неправильную дробь. Иными словами, определить, сколько восьмых долей содержится в четырёх и пяти восьмых. Так как одной единице соответствует 8 / 8, то четырём — 8 * 4 / 8 = 32 / 8. Соответственно в четырёх и 5 / 8 будет 37 / 8 долей.
Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:
- перемножить единицы целой части со знаменателем дробного числа;
- сложить полученное произведение и числитель дроби;
- результат сложения записать в числитель, а знаменатель оставить без изменений.
Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.
Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.
Выполнение действий
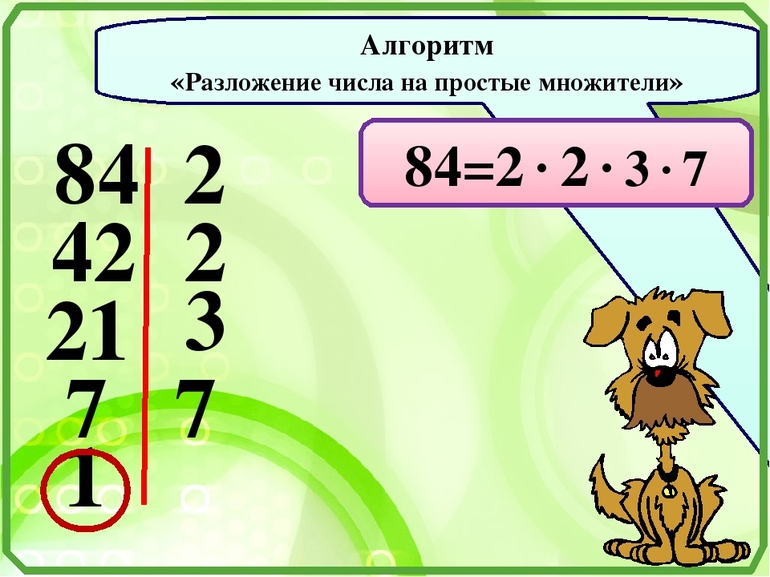
Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.
Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.
Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:
- исследовать числитель и знаменатель на возможность сокращения;
- определить наименьший общий знаменатель (НОЗ) среди делителей;
- найти дополнительные множители;
- выполнить умножение числителей на найденные аргументы;
- в знаменатель записать НОЗ, а в числитель сумму или разность произведений делимых.
Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).
Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).
Возведение в степень и извлечение корня выполняют способом разделения. То есть, делимое от делителя возводится или извлекается отдельно: (s / m) j = sj / mj и √(s / m) = √s / √m. Например, 3 / 2 * 9 / 6 : 7 / 5 * (3 / 2)3. С какого действия начинать решение не принципиально, но следует обратить внимание, что 9 / 6 можно сократить на три. В итоге получится 9 / 6 = 3 / 2. Далее, решение будет выглядеть следующим образом: 3 / 2 * 3 / 2 : 7 / 5 * 3 3 / 23 = (3 * 3) / (2 * 2): 7 / 5 * 27 / 8 = 9 / 4 * 5 / 7 * 27 / 8 = (9 * 5 * 27) / (4* 7 * 

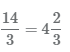
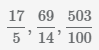 в смешанные числа.
в смешанные числа.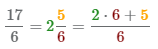
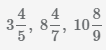 в неправильные дроби.
в неправильные дроби.