Тема: Найти наибольшую и наименьшую длину волны (Прочитано 14370 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Найти наибольшую и наименьшую длину волны в инфракрасной серии линий спектра излучения атома водорода (серия Пашена)
« Последнее редактирование: 27 Января 2015, 22:53 от Ost »
Записан
Решение.
Для атома водорода справедлива формула Бальмера для определения длины волны:
[ begin{align}
& nu =ccdot Rcdot (frac{1}{{{m}^{2}}}-frac{1}{{{n}^{2}}}), nu =frac{c}{lambda }, \
& frac{1}{{{lambda }_{nm}}}=Rcdot (frac{1}{{{m}^{2}}}-frac{1}{{{n}^{2}}}), {{lambda }_{nm}}=frac{1}{Rcdot (frac{1}{{{m}^{2}}}-frac{1}{{{n}^{2}}})} (1). \
& frac{1}{{{lambda }_{min }}}=frac{R}{{{m}^{2}}}, n=infty . \
& {{lambda }_{min }}=frac{{{m}^{2}}}{R} (2). \
end{align} ]
В серии Пашена электрон переходит на третий энергетический уровень, m = 3.
Для определения максимальной длины волны n = 4.
с = 3∙108 м/с, с – скорость света, R – постоянная Ридберга,
R = 1,097737∙107 м-1.
λmах = 18,74∙10-7 м.
λmin = 8,198∙10-7 м.
« Последнее редактирование: 26 Февраля 2015, 06:32 от alsak »
Записан
To use your Google Account on a browser (like Chrome or Safari), turn on cookies if you haven’t already.
Important: If you get a message that cookies are turned off, you need to turn them on to use your account.
In Chrome
- On your computer, open Chrome.
- At the top right, click More
Settings.
- Under «Privacy and security,» click Site settings.
- Click Cookies and site data.
- From here, you can:
- Turn on cookies: Next to «Blocked,» turn on the switch.
- Turn off cookies: Turn off Allow all cookies.
Learn how to change more cookie settings in Chrome.
In other browsers
For instructions, check the support website for your browser.
Why cookies are helpful
Cookies are files created by sites you visit. They make your online experience easier by saving browsing information. With cookies, sites can:
- Keep you signed in
- Remember your site preferences
- Give you locally relevant content
We use cookies to improve our services. To learn more, read our Privacy Policy.
Fix problems
If you can’t use your Google Account and get a message that cookies are turned off:
- Follow the steps above to turn on cookies.
- Try signing in again.
If you still get the error message, here are some possible solutions. Try each one, then try signing in.
- Open a new browser window.
- Clear your browser’s cache and cookies. Learn how to clear cache and cookies.
- Browse in private. Learn how to browse privately in Chrome.
- Change your browser’s privacy settings. Learn how to change privacy settings.
Was this helpful?
How can we improve it?
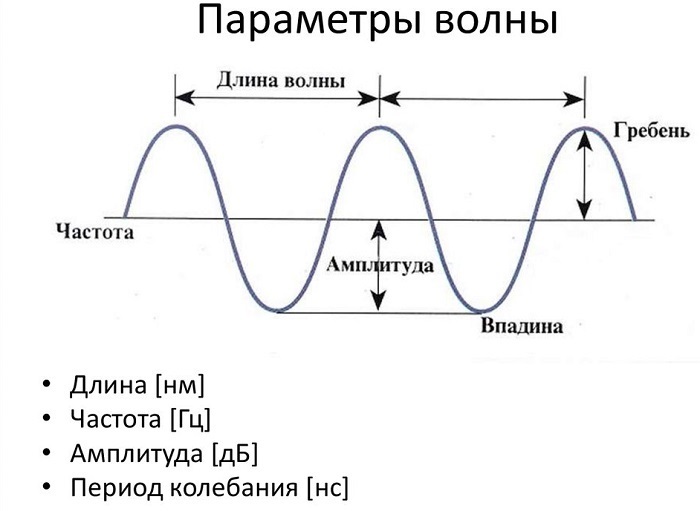
Длина волны — это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной.
Цикл — это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.
На рисунке показаны основные параметры волны, используемые в физике:
Определение и формула длины волн
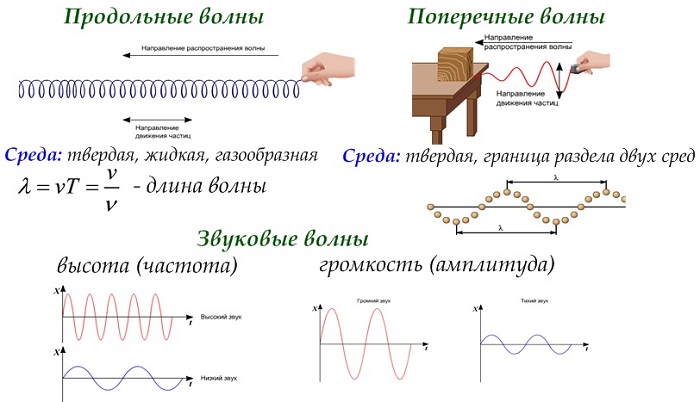
Волна — это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества.
Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.
Греческая буква «λ» (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.
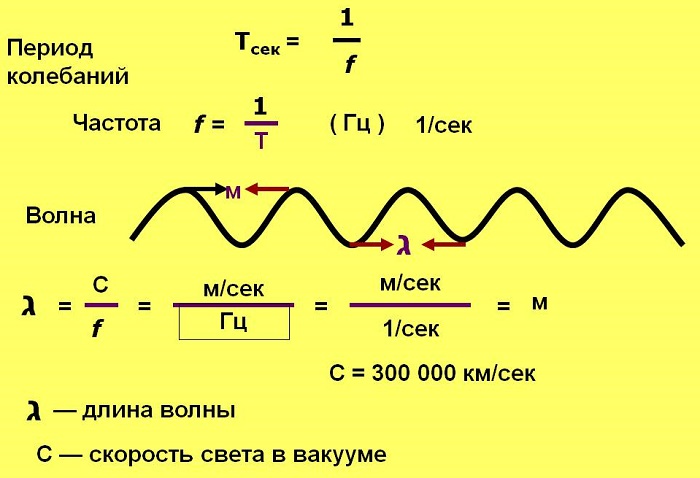
Период Т — время завершения полного колебания, единица измерения секунды (с).
Длинная волна соответствует низкой частоте, а короткая — высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.
У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.
Пространственный период волны — это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.
Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).
При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).
Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 108 м/с поделить на длину в метрах.
Единицы измерения длины волны λ — нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).
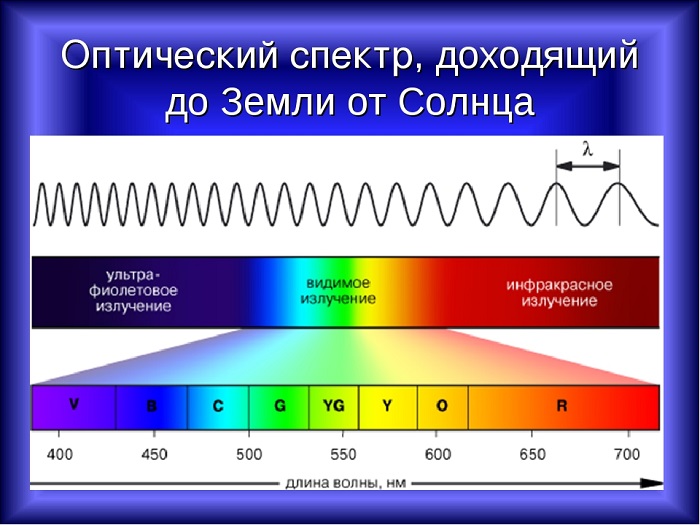
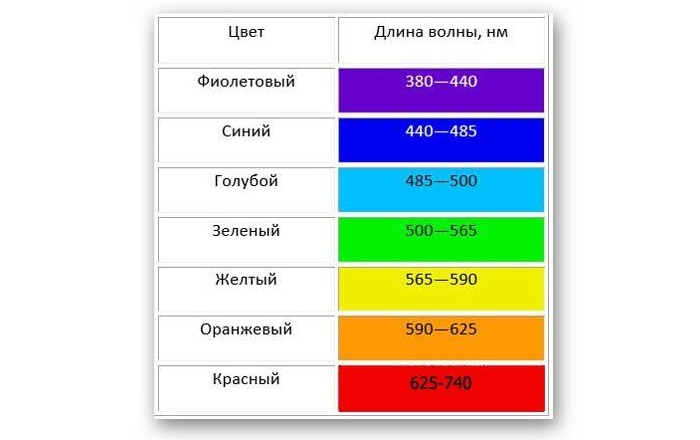
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.
Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной — красный, который составляет около 700 нм.
Таблица показывает длину волны в зависимости от цвета:
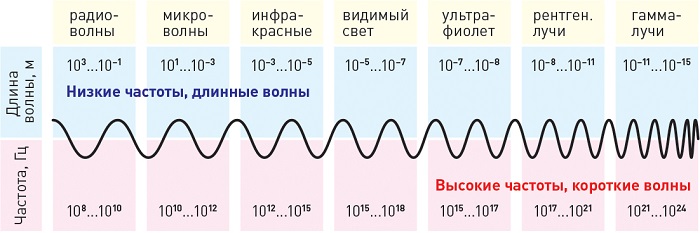
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания.
Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.
Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Слайд 1Примеры решения задач.
Водородоподобные атомы.
Оптические спектры излучения.
6.7.

Слайд 2А1. Найти радиусы rk трёх первых боровских электронных орбит в
атоме водорода и скорости vk электрона на них.
Дано:
k1 = 1
k3
= 3
rk — ?
Vk — ?
Решение.
Здесь n – целое число, Z = 1.
Согласно теории Бора, электрон в атоме водорода может находиться на орбитах с радиусами
Радиус орбиты произвольного состояния с любым номером n удобно выражать через радиус первой боровской орбиты:
Для атома водорода (Z = 1)
(м).
(м).
(м).

Слайд 3Скорость электрона в атоме водорода определим из второго закона Ньютона.
А1. Найти радиусы rk трёх первых боровских электронных орбит в
атоме водорода и скорости vk электрона на них.
Решение (продолжение).
где V — скорость электрона, R — радиус орбиты, Z = 1.
(м).
(м).
(м).

Слайд 4Ответ: r1 = 53 пм; r2 = 212 пм; r3
= 477 пм; v1 = 2,19·106 м/с; v2 = l,1·
106 м/c;
v3 =7,3 ·105 м/c.
А1. Найти радиусы rk трёх первых боровских электронных орбит в атоме водорода и скорости vk электрона на них.
Решение (продолжение).
(м/c).
(м/c).
(м/c).

Слайд 5А2. Найти период Т обращения электрона на первой боровской орбите
атома водорода и его угловую скорость ω.
Дано:
n = 1
Z =
1
T — ?
ω — ?
Решение.
Угловую скорость электрона в атоме водорода определим из второго закона Ньютона.
где ω — скорость электрона, R — радиус орбиты, Z = 1.
(рад/c).

Слайд 6А2. Найти период Т обращения электрона на первой боровской орбите
атома водорода и его угловую скорость
Ответ: Т =1,43·10-16 с;
ω = 4,4·1016 рад/с.
Период обращения по орбите связан с угловой скоростью простым соотношением:
Решение (продолжение).

Слайд 7B2. Определить ток, соответствующий движению электрона по п-й орбите атома
водорода.
Решение .
Ток, связанный с движением электрона в атоме водорода
Угловую
скорость электрона ω в атоме водорода определим из второго закона Ньютона.
Δq – заряд, проходящий через поперечное сечение проводника за время Δt.
В качестве сечения проводника рассмотрим плоскость AB на рисунке. Её пересекает один электрон за время, равное периоду обращения электрона вокруг ядра.
где ω — скорость электрона, R — радиус орбиты, Z = 1.

Слайд 8B2. Определить ток, соответствующий движению электрона по п-й орбите атома
водорода.
Решение (продолжение) .
n – целое число.
Согласно теории Бора,
электрон в атоме водорода может находиться на орбитах с радиусами

Слайд 9B2. Определить ток, соответствующий движению электрона по п-й орбите атома
водорода.
Решение (продолжение) .
Ответ: I1 =1,06·10-2 A.

Слайд 10B1. Фотон с энергией E = 16,5 эВ выбивает электрон
из невозбуждённого атома водорода. Какую скорость будет иметь электрон вдали
от ядра?
Дано:
E = 16,5 эВ
n = 1
V — ?
Решение.
После поглощения атомом фотона энергия электрона станет
Энергия электрона в основном состоянии в атоме водорода
Энергия электрона больше нуля, следовательно, он удалится от ядра атома на сколь угодно большое расстояние. При этом его потенциальная энергия станет равной нулю, а кинетическая
Скорость электрона на большом удалении от ядра
(эВ).
(эВ).
Ответ: v =1·106 м/с.
(м/с).

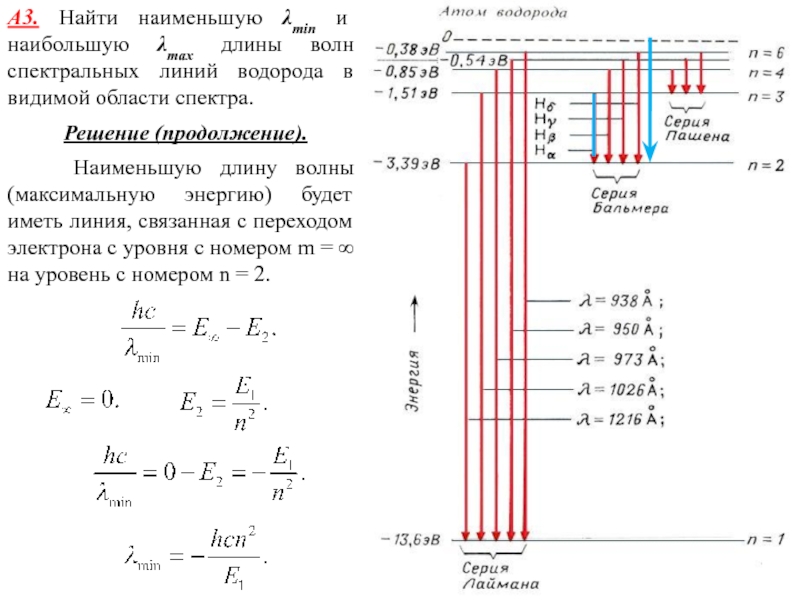
Слайд 11А3. Найти наименьшую λmin и наибольшую λmax длины волн спектральных
линий водорода в видимой области спектра.
Решение.
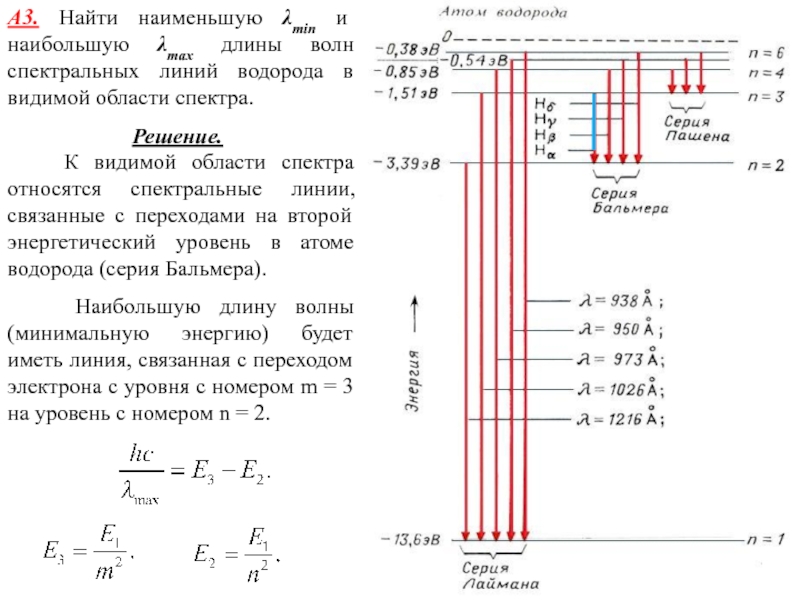
К видимой области
спектра относятся спектральные линии, связанные с переходами на второй энергетический уровень в атоме водорода (серия Бальмера).
Наибольшую длину волны (минимальную энергию) будет иметь линия, связанная с переходом электрона с уровня с номером m = 3 на уровень с номером n = 2.
Слайд 12А3. Найти наименьшую λmin и наибольшую λmax длины волн спектральных
линий водорода в видимой области спектра.
Решение (продолжение).
(м).
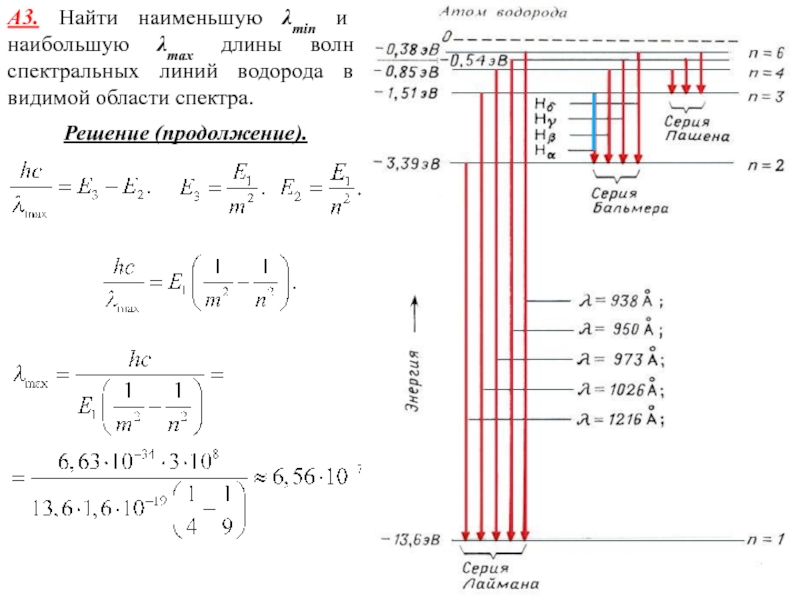
Слайд 13А3. Найти наименьшую λmin и наибольшую λmax длины волн спектральных
линий водорода в видимой области спектра.
Наименьшую длину волны
(максимальную энергию) будет иметь линия, связанная с переходом электрона с уровня с номером m = ∞ на уровень с номером n = 2.
Решение (продолжение).
Слайд 14Ответ: λmin =365 нм; λmax =656 нм.
А3. Найти наименьшую λmin
и наибольшую λmax длины волн спектральных линий водорода в видимой
области спектра.
Решение (продолжение).
(м).

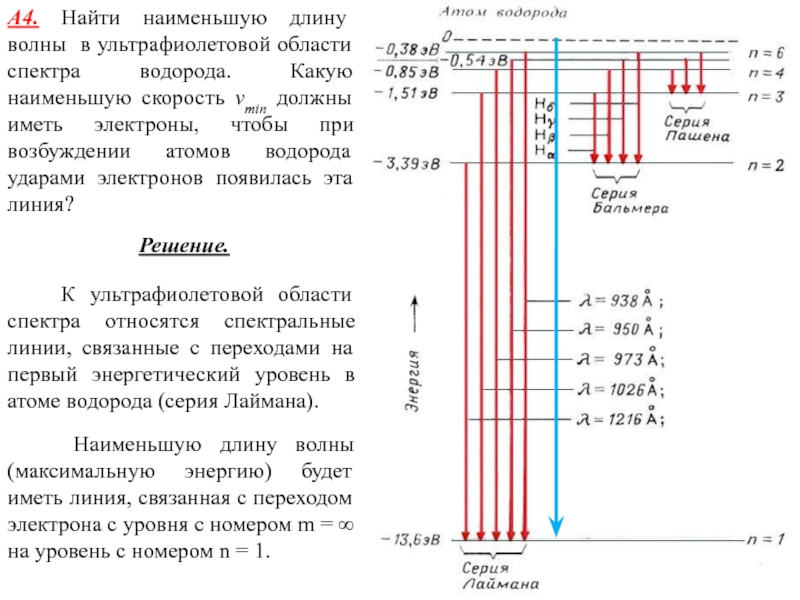
Слайд 15А4. Найти наименьшую длину волны в ультрафиолетовой области спектра водорода.
Какую наименьшую скорость vmin должны иметь электроны, чтобы при возбуждении
атомов водорода ударами электронов появилась эта линия?
Решение.
К ультрафиолетовой области спектра относятся спектральные линии, связанные с переходами на первый энергетический уровень в атоме водорода (серия Лаймана).
Наименьшую длину волны (максимальную энергию) будет иметь линия, связанная с переходом электрона с уровня с номером m = ∞ на уровень с номером n = 1.
Слайд 16А4. Найти наименьшую длину волны в ультрафиолетовой области спектра водорода.
Какую наименьшую скорость vmin должны иметь электроны, чтобы при возбуждении
атомов водорода ударами электронов появилась эта линия?
Решение (продолжение).
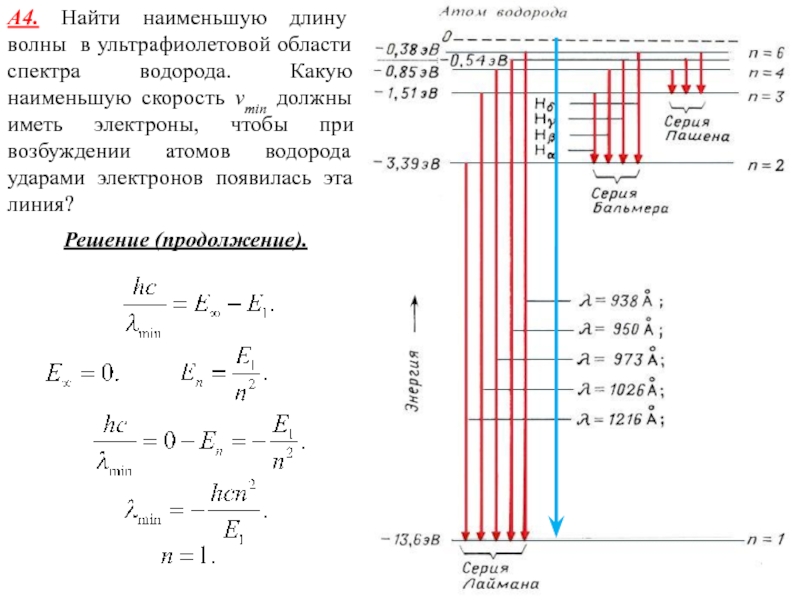
Слайд 17Ответ: λ = 91,4 нм; Vmin =2,20·106 м/с.
А4. Найти наименьшую
длину волны в ультрафиолетовой области спектра водорода. Какую наименьшую скорость
vmin должны иметь электроны, чтобы при возбуждении атомов водорода ударами электронов появилась эта линия?
(м).
Решение (продолжение).
При возбуждении атома электронными ударами кинетическая энергия электрона должна быть больше (или равна) энергии возбуждения.
(эВ).
(м/с).

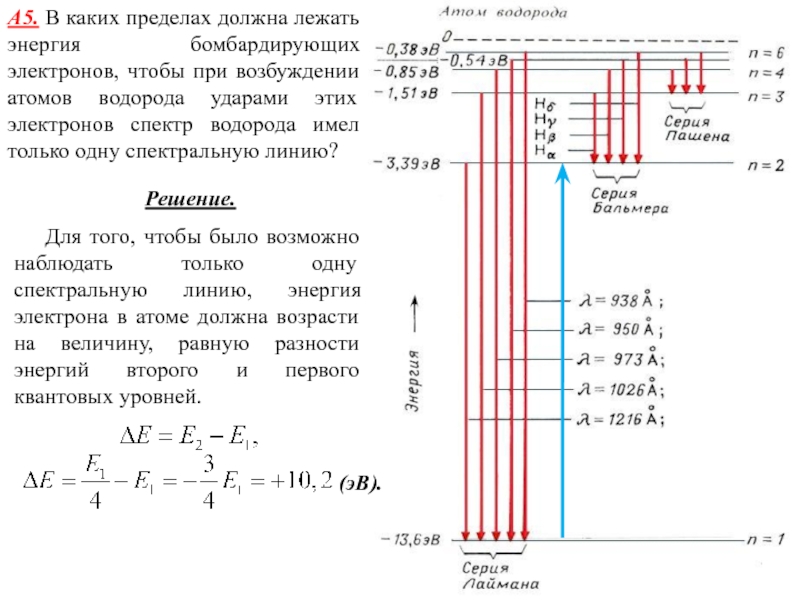
Слайд 18А5. В каких пределах должна лежать энергия бомбардирующих электронов, чтобы
при возбуждении атомов водорода ударами этих электронов спектр водорода имел
только одну спектральную линию?
Решение.
Для того, чтобы было возможно наблюдать только одну спектральную линию, энергия электрона в атоме должна возрасти на величину, равную разности энергий второго и первого квантовых уровней.
(эВ).
Слайд 19А5. В каких пределах должна лежать энергия бомбардирующих электронов, чтобы
при возбуждении атомов водорода ударами этих электронов спектр водорода имел
только одну спектральную линию?
Решение (продолжение).
При столкновении бомбардирую-щий электрон не может передать энергию, большую, чем кинетическая энергия этого электрона, поэтому.
(эВ).
В то же время электрон атома не должен получить энергию, достаточную для перехода на уровень номер 3.
(эВ).

Слайд 20А5. В каких пределах должна лежать энергия бомбардирующих электронов, чтобы
при возбуждении атомов водорода ударами этих электронов спектр водорода имел
только одну спектральную линию?
Решение (продолжение).
Таким образом, энергия бомбардирующего электрона должна быть меньше энергии, достаточную для перехода электрона в атоме на уровень номер 3.
эВ
(эВ).
Ответ: энергия бомбардирующих электронов должна лежать в пределах
эВ.

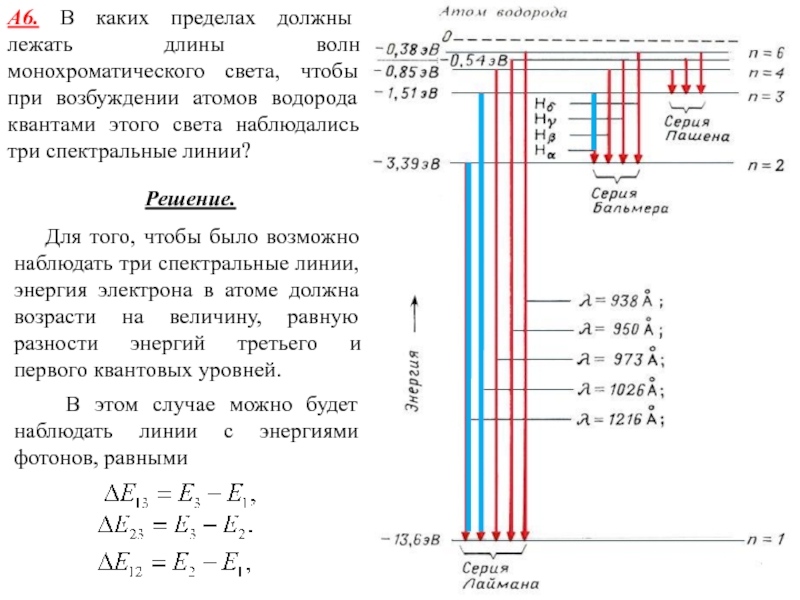
Слайд 21А6. В каких пределах должны лежать длины волн монохроматического света,
чтобы при возбуждении атомов водорода квантами этого света наблюдались три
спектральные линии?
Решение.
Для того, чтобы было возможно наблюдать три спектральные линии, энергия электрона в атоме должна возрасти на величину, равную разности энергий третьего и первого квантовых уровней.
В этом случае можно будет наблюдать линии с энергиями фотонов, равными
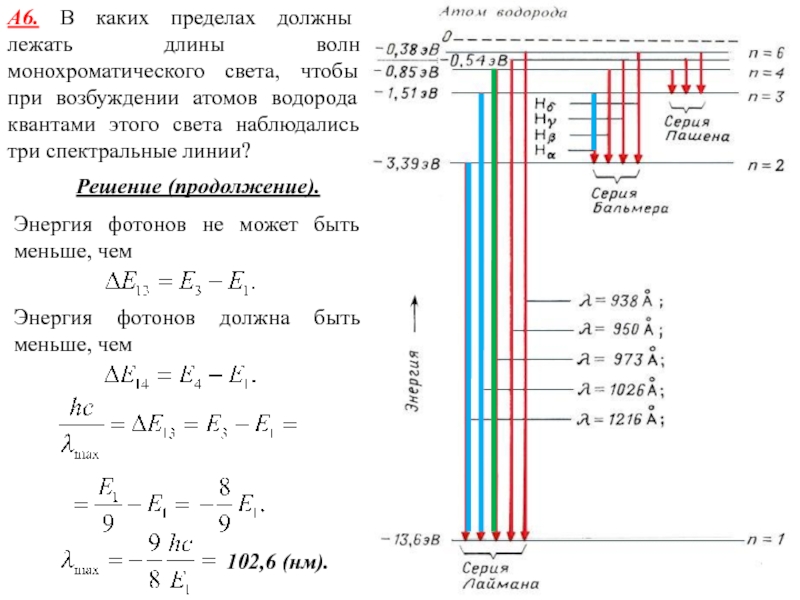
Слайд 22А6. В каких пределах должны лежать длины волн монохроматического света,
чтобы при возбуждении атомов водорода квантами этого света наблюдались три
спектральные линии?
Решение (продолжение).
Энергия фотонов не может быть меньше, чем
Энергия фотонов должна быть меньше, чем
102,6 (нм).
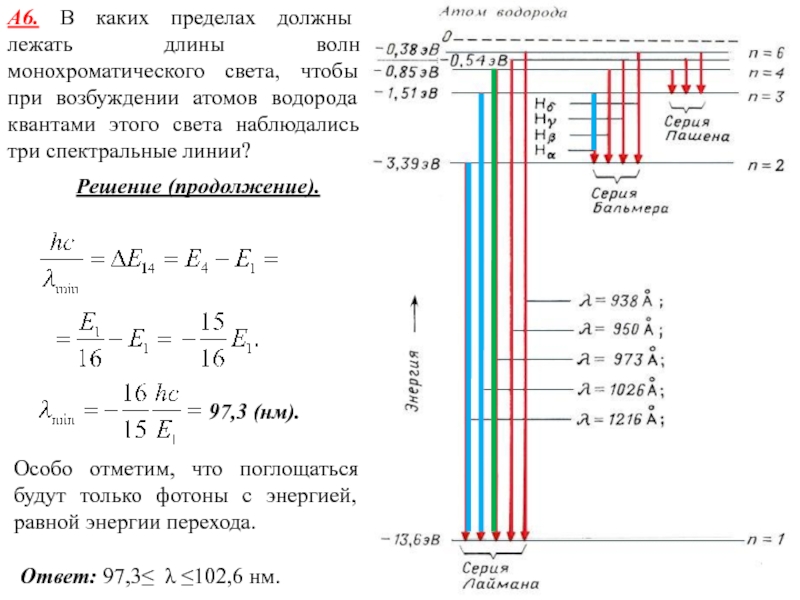
Слайд 23А6. В каких пределах должны лежать длины волн монохроматического света,
чтобы при возбуждении атомов водорода квантами этого света наблюдались три
спектральные линии?
Ответ: 97,3≤ λ ≤102,6 нм.
97,3 (нм).
Решение (продолжение).
Особо отметим, что поглощаться будут только фотоны с энергией, равной энергии перехода.
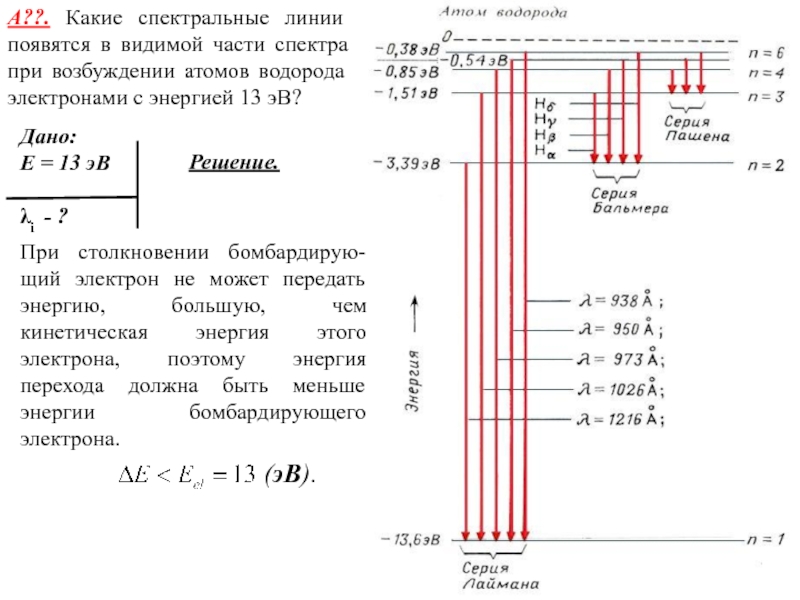
Слайд 24А??. Какие спектральные линии появятся в видимой части спектра при
возбуждении атомов водорода электронами с энергией 13 эВ?
Дано:
Е = 13
эВ
λi — ?
Решение.
При столкновении бомбардирую-щий электрон не может передать энергию, большую, чем кинетическая энергия этого электрона, поэтому энергия перехода должна быть меньше энергии бомбардирующего электрона.
(эВ).
Слайд 25(эВ).
А??. Какие спектральные линии появятся в видимой части спектра при
возбуждении атомов водорода электронами с энергией 13 эВ?
Решение (продолжение).
Проверим, какие
переходы удовлетворяют этому условию.
(эВ).
(эВ).
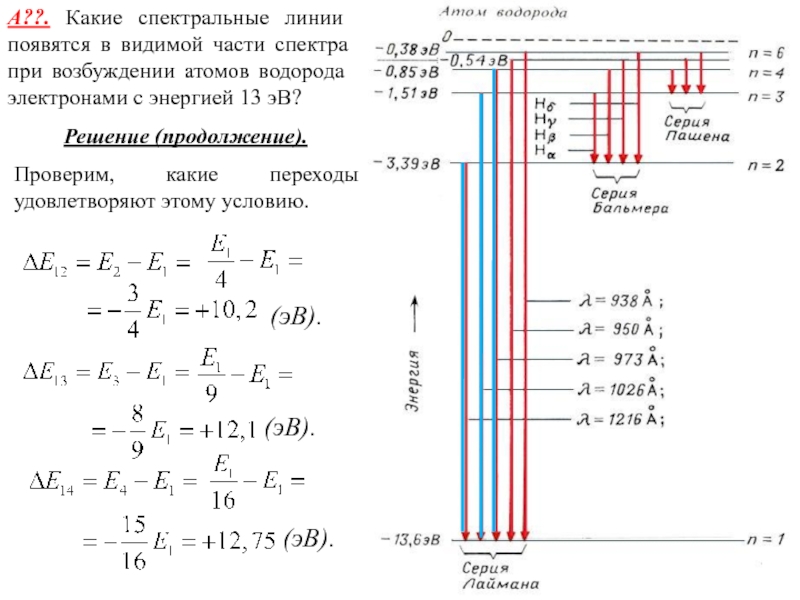
Слайд 26(эВ).
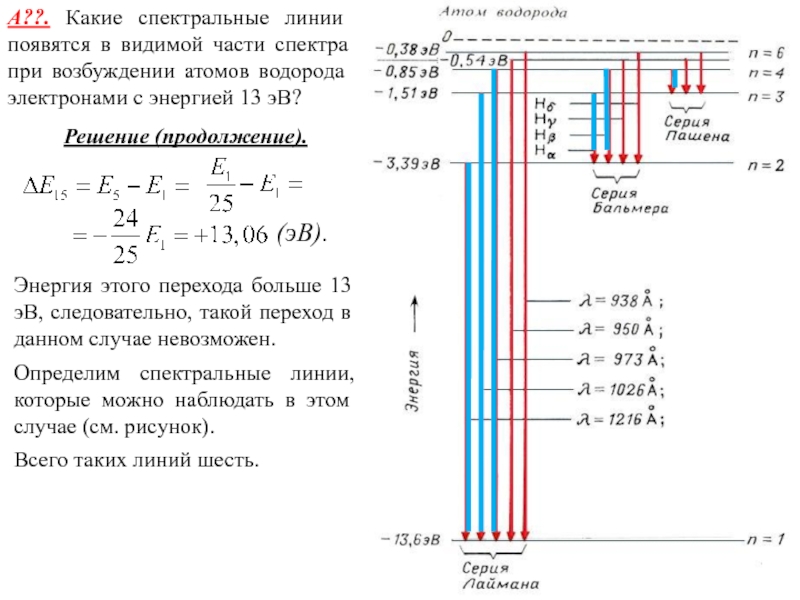
А??. Какие спектральные линии появятся в видимой части спектра при
возбуждении атомов водорода электронами с энергией 13 эВ?
Решение (продолжение).
Энергия этого
перехода больше 13 эВ, следовательно, такой переход в данном случае невозможен.
Определим спектральные линии, которые можно наблюдать в этом случае (см. рисунок).
Всего таких линий шесть.
В этой статье мы собираемся обдумать взаимосвязь энергии и длины волны вместе с примерами и решить некоторые задачи, чтобы проиллюстрировать то же самое.
Энергия находится в прямой зависимости от частоты электромагнитных излучений. Если длина волны увеличивается, это означает, что повторяемость волны будет уменьшаться, что непосредственно влияет на энергию частицы в волне.
Формула соотношения энергии и длины волны
Энергия частицы может быть связана с ее скоростью во время распространения. Скорость частицы дает представление о частоте и длине волны. Если длина волны мала, то частота и, следовательно, энергия частицы будут увеличиваться.
Если колебания частицы больше в траектории пути, то возвратность частицы в волну больше и длина волны мала, это означает, что энергия, которой обладает частица, больше.
Энергия любого тела связана с его длиной волны уравнением
E=hc/λ
Где «h» — постоянная Планка h = 6.626 * 10-34Js
C — скорость света c=3 *108 м/с и
λ — длина волны света
Энергия обратно пропорциональна длине волны света. Чем меньше длина волны, тем больше энергия частицы в волне.
Задача 1: Рассчитать энергию фотонов, испускающих красный свет. Считайте длину волны луча красного света равной 698 нм. Какова будет энергия, если длина волны уменьшится до 500 нм, то есть если источник излучает зеленый свет?
Данный:λ1=698нм
λ2=500 нм
ч = 6.626 * 10-34 Js
с=3 * 108 м/с
У нас есть,
E=hc/λ1
E = 6.626 * 10-34 Дж* 3 * 108 м/с/698* 10-9m
=0.028* 10-17=28* 10-20Дж
Энергия красной длины волны 28* 10-20Джоули.
Если длина волны λ2=500 нм
Тогда энергия, связанная с зеленым светом, равна
E=hc/λ2
E = 6.626 * 10-34 Дж* 3 * 108 м/с / 500* 10-9m
= 0.03910-17=39* 10-20Дж
Мы видим, что энергия увеличилась до 39*10-20 Джоулей при уменьшении длины волны.
Подробнее о Влияние преломления на длину волны: как, почему, подробные факты.
График взаимосвязи энергии и длины волны
По мере увеличения длины волны частота волны падает, тем самым уменьшая энергию, которой обладает волна. Если мы построим график зависимости энергии от длины волны появляющейся частицы, то график будет выглядеть так, как показано ниже.
Приведенный выше график ясно показывает, что по мере увеличения длины волны энергия, связанная с частицей, уменьшается экспоненциально.
Связь кинетической энергии и длины волны
Если скорость частицы больше, то очевидно, что кинетическая энергия частицы велика. Кинетическая энергия определяется уравнением
КЭ=1/2мВ2
Где m — масса объекта или частицы
V — скорость массы
Мы можем записать приведенное выше уравнение как
2E=мв2
Умножение «m» в обеих частях уравнения
2mE=(мВ)2
Импульс объекта определяется как произведение массы объекта на скорость, с которой он движется.
p = mv
Следовательно, приведенное выше уравнение становится
P2=2 мВ
P=√2mE
Согласно де Бройлю,
λ =h/p
Подставляя приведенное выше уравнение, мы имеем
λ =h/ √2mE
Приведенное выше уравнение дает связь между энергией и длиной волны частицы.
Подробнее о Что такое кинетическая энергия света: подробные факты.
Задача 2. Вычислить кинетическую энергию частицы массой 9.1 × 10-31 кг с длиной волны 293 нм. Кроме того, найдите скорость частицы.
Данный: λ = 293 нм
м = 9.1 × 10-31 kg
ч = 6.626 * 10-34Js
с=3 *108 м/с
У нас есть,
λ =h/ √2mE
λ2=h2/ 2мЕ
Е = ч2/ 2мλ2
=(6.626 * 10-34 Дж)2/2* 9.1* 10-31* (293*10-9) 2
= 0.28 * 10-23
Кинетическая энергия, связанная с частицей, равна 0.28*10-23 Джоули.
Теперь, чтобы вычислить скорость частицы, выведем формулу скорости из кинетической энергии:
КЕ=1/2 мВ2
2E= мв2
v=√(2Е/м)
= √(2(0.28*10-23)/(9.8*10-31))
= 0.24 * 104= 2400 м / с
Скорость частицы с длиной волны 298 нм составляет 2400 м/с.
Связь энергии электрона и длины волны
Энергия электрона определяется простым уравнением:
Е=чню
Где «h» — постоянная Планка, а
nu — частота появления электрона
Частота электрона определяется как
ню = v / λ
Где v — скорость электрона и
λ — длина волны электронной волны
Следовательно, энергия связана с длиной волны электрона как
E=hv/λ
Это соотношение позволяет найти энергию, связанную с распространением одиночного электрона с определенной длиной волны, скоростью и частотой. Энергия обратно пропорциональна длине волны. Если длина волны электрона уменьшается, энергия волны должна быть больше.
Изображение Фото: Pixabay
Получив энергию в той или иной форме, электрон переходит из более низкого энергетического состояния в более высокое энергетическое состояние. Для перехода электронов из одного состояния в другое энергия электрона определяется уравнением
Э=РE(1/нf– 1/нi)
Где RE=-2.18* 10-18m-1 является константой Ридберга
nf это конечное состояние электрона
ni это начальное состояние электрона
Мы можем далее переписать приведенное выше уравнение как
ч ню = RE(1/нf– 1/нi)
hc/λ =RE(1/нf– 1/нi)
1/λ =REhc(1/nf– 1/нi)
1/λ =R(1/nf– 1/нi)
Где,
Р=РEчс=1.097* 107
По мере того, как электрон получает энергию, электрон переходит и перескакивает в более высокое состояние энергетического уровня и высвобождает энергию электронам, присутствующим в этом состоянии, и либо становится стабильным, либо высвобождает количество энергии и возвращается в более низкие энергетические состояния.
Подробнее о 16+ Пример амплитуды волны: подробные пояснения.
Задача 3: Если электрон переходит из состояния ni=1, чтобы указать nf=2, затем рассчитайте длину волны электрона.
Данный:
ni=1
nf=2
1/λ =RE(1/нf– 1/нi)
1/λ=-1.097*107 * ( 1/2-1/1 )
1/λ=0.5485* 107
Следовательно,
λ = 1/0.5485* 107
λ =1.823*10-7
λ =182.3*10-9=182.3нм
Длина волны света, излучаемого при переходе электрона с одного энергетического уровня на другой, равна 182.3 нм.
Связь лучистой энергии и длины волны
Каждый объект поглощает световые лучи в дневное время в зависимости от его формы, размера и состава. Если температура поверхности объекта достигает температуры выше абсолютного нуля, объект будет излучать излучения в виде волн.
Это испускаемое излучение пропорционально четвертой степени абсолютной температуры объекта и определяется уравнением
U=ɛΣ Т4A
Где U — излучаемая энергия
ɛ — коэффициент излучения излучения от объекта
Σ — постоянная Стефана-Больцмана, равная Σ=5.67*10-8Вт / м2K4
T — абсолютная температура
А — площадь объекта
Объект с высокой температурой излучает излучение с короткими длинами волн, а более холодные поверхности излучают волны с большей длиной волны. В зависимости от испускаемого излучения и длины волны испускаемого излучения волны классифицируются в соответствии с приведенной ниже таблицей.
| Имя и фамилия | Радиоволны | Микроволны | Инфракрасный порт | Видимый | Ультрафиолетовое | рентген | Гамма излучение |
| Длина волны | > 1м | 1mm-1m | 700нм-1мм | 400nm-700nm | 10nm-380nm | 0.01nm-10nm | <0.01 нм |
| частота | <300 МГц | 300MHz-300GHz | 300ГГц-430ТГц | 430ТГц-750ТГц | 750ТГц-30ФГц | 30PHz-30EHz | >30 Гц |
По мере уменьшения длины волны излучения частота волны возрастает. Длина волны напрямую связана с температурой, поэтому, если частота испускаемого излучения больше, это означает, что энергия объекта высока.
Гамма-лучи, рентгеновские лучи и ультрафиолетовые лучи имеют очень короткую длину волны, поэтому энергия этих волн очень высока по сравнению с видимым, инфракрасным, микроволнами или радиоволнами. Кроме того, чем выше излучение, полученное объектом, тем больше он будет излучать в зависимости от коэффициента излучения объекта.
Ниже приведен график зависимости энергии от длины волны в секунду для разных температур. График показывает, что по мере повышения температуры системы энергия испускаемого излучения также увеличивается с температурой.
Для длины волны в видимой области эмиссия излучения максимальна. Это связано с тем, что Солнце излучает УФ-лучи вместе с инфракрасными лучами и видимыми лучами, а эти лучи представляют собой электромагнитные волны дальнего действия. Озоновый слой Земли защищает земную атмосферу от этого вредного излучения и либо отражается обратно, либо задерживается в облаках.
В видимом диапазоне в дневное время излучается больше излучений, поскольку в дневное время от Солнца поступает все больше и больше излучений, а испускается меньше ИК-лучей по сравнению с видимым спектром. Ночью температура снижается, длина волны излучения увеличивается, и объект излучает больше ИК-лучей.
Подробнее о Свойства преломления: волна, физические свойства, исчерпывающие факты.
Задача 4: Коробка длиной 11 см, шириной 2 см и воздухом 7 см нагревается до температуры 1200 Кельвинов. Если коэффициент излучения ящика равен 0.5, то рассчитайте скорость излучения энергии из ящика.
Данный:л=11см
ч=2см
б = 7cm
е =0.5
Σ=5.67* 10-8Вт / м2K4
Т=1200 К
Общая площадь ящика составляет
A=2(фунт+чб+гл)
=2(11*7+7*s 2+2*11)
=2 (77+14+22)
=0.0226 кв.м
Энергия, излучаемая коробкой, равна
U=ɛ Σ T4A
=0.5* 5.67* 10-8* 12004* 0.0226
=1328.6 Вт
Связь частоты энергии и длины волны
Чем больше частота волны, тем больше энергия, связанная с частицей. Энергия связана с частотой волны как
E=ч/ню
Где «h» — постоянная Планка.
nu — частота волны
Частота волны определяется как скорость волны в среде и длина волны.
ню = v / λ
Где v — скорость волны
λ — длина волны
Следовательно,
λ=v/ну
Это дает связь между частотой и длиной волны волны. Это говорит о том, что длина волны и частота обратно пропорциональны друг другу. Если длина волны увеличивается, частота волны уменьшится.
Подробнее о Влияние преломления на частоту: как, почему нет, подробные факты.
Задача 5. Скорость луча света, испускаемого источником, равна 1.9 × 108 РС. Частота возникновения излучаемой волны составляет 450ТГц. Найдите длину волны испускаемого излучения.
Данный: v=1.9*108 м/с
F=450ТГц=450*1012Hz
Длина волны луча света равна
λ = v/f
=1.9* 108/ 450* 1012
= 0.004222 * 10-4
=422.2* 10-9=422.2нм
Луч света имеет длину волны 422.2 нм.
Связь энергии фотона и длины волны
Энергия, которой обладает фотон, называется энергией фотона и обратно пропорциональна электромагнитной волне фотона по соотношению
E=hc/λ
Где «h» — постоянная Планка.
С — скорость света
λ — длина волны фотона
Частота фотона определяется уравнением
f=с/λ
Где f — частота
Следовательно, фотон с большей длиной волны обладает небольшой единицей энергии, тогда как фотон с меньшей длиной волны дает большое количество энергии.
Подробнее о Какова длина волны фотона: как найти, несколько идей и фактов.
Задача 6: Рассчитать энергию фотона, распространяющегося в электромагнитной волне с длиной волны 620 нм.
Данный: Длина волныλ =620 нм
ч = 6.626 * 10-34 js
с=3 *108 м/с
У нас есть,
E=hc/λ
Е=6.626 * 10-34 Дж*3 * 108 м/с/620* 10-9m
= 0.032 * 10-17= 32 * 10-20 Дж
Энергия, связанная с фотоном, равна 32* 10-20Джоули.
Часто задаваемые вопросы
Q1. Вычислите длину волны электрона, движущегося со скоростью 6.35 × 106 м/с
Данный: v=6.35*106м/с
м=9.1*10-31kg
ч=6.62* 10-34 Js
Кинетическая энергия электрона равна
КЕ=1/2 мВ2
=1/2 * 9.1*10-31* (6.35* 106)2
=1.83* 10-17Дж
Импульс электрона равен
P=√2mE
=√2* 9.1* 10-31* 1.83 * 10-17
= 5.7 * 10-24кг.м / с
Теперь длина волны электрона
λ =h/√2mE
= 6.62 * 10-34/ 5.7 * 10-24
= 4.8 * 10-10m
=48нм
Длина волны электрона, движущегося со скоростью 6.35*106м/с составляет 48 нм.
Q2. Черный объект площадью 180 кв.м находится при температуре 550К. Какова скорость излучения энергии от объекта?
Данный: А=180 кв.м
Т=550К
Поскольку объект имеет черный цвет, коэффициент излучения равен 1.
е =1
У нас есть,
U=ɛΣT4A
=1*с 5.67* 10-8* 5504* 180
= 0.93 * 106МОЩНОСТЬ
Мощность излучения от выброса излучения от объекта составляет 0.93*106Вт.
Какова абсолютная температура системы?
Это неизменное и совершенное значение температуры системы.
Абсолютная температура системы измеряется по шкале градусов Цельсия, Фаренгейта или Кельвина, которые измеряют ноль как абсолютный ноль градусов.
Как длина волны фотона зависит от температуры?
Температура системы определяет подвижность частиц системы.
Чем больше излучений получает система при более высоких температурах, тем больше излучения будет излучаться системой. При более высоких температурах излучаются более короткие волны, а при более низких температурах излучаются более длинные волны.