Видеоурок как найти общий знаменатель дробей
Как найти общий знаменатель. Математика 6 класс просто
КАК НАЙТИ ОБЩИЙ ЗНАМЕНАТЕЛЬ ДРОБЕЙ НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ МАТЕМАТИКА 5 КЛАСС
16 — Как приводить дроби к общему знаменателю — Часть 1 ( Математика — 5 класс )
Как найти общий знаменатель, что такое общий знаменатель и конечно же нахождение общего знаменателя онлайн на нашем калькуляторе. И если вам требуется наименьший общий знаменатель, то он тут.
Что такое общий знаменатель?
Кроме понятия «общий знаменатель«, есть еще такое понятие как — «Наименьший общий знаменатель (НОЗ)» — это… тоже самое, что и «НОК». Поэтому, мы не будем это разбирать здесь второй раз.
Но что такое общий знаменатель простыми словами?
Общий знаменатель — это любое целое число, которое делится без остатка на первый и второй знаменатель.
Количество чисел, которые могут быть общим знаменателем стремится к бесконечности, но обычно общим знаменателем принимают НОЗ
Пример общего знаменателя :
Для того, чтобы понять, «что такое общий знаменатель» нам нужен пример двух дробей и какое-то действие(иначе смысла в этом нет), пусть это будут две дроби 1/2 и 1/3 и действие сложение — «+».
Для таких маленьких чисел, как 2 и 3 — «нок» будет равен 6. Для этого нам никакие инструменты не понадобятся, наверняка вы это тоже смогли посчитать в уме.
Т.е. 6 делится на 2 без остатка 6 : 2 = 3, и 6 делится на 3 без остатка 6 : 3 = 2.
Мы получили два числа, первую дробь 1/2 надо умножить на 3, чтобы привести её к общему знаменателю 6 — 1*3/2*3 = 3/6.
А вторую дробь нужно умножить на 2, чтобы привести и её к общему знаменатель 6, 1*2/3*2 = 2/6.
После того, как мы нашли общий знаменатель, мы можем произвести действие, в нашем случае — «+» — 3/6 + 2/6 = (3 + 2)/6 = 5/6.
Когда мы нашли «общий знаменатель» мы смогли выполнить необходимое действие с дробями.
1 2 + 1 3 =
1*3 2*3 + 1*2 3*2 =
3 6 + 2 6 =
3 + 2 6 =
5 6
В каком случае ноз двух дробей будет являться произведением знаменателей?
Отличный поисковый запрос — «в каком случае ноз двух дробей будет являться произведением знаменателей?«, что выше не было озвучено.
Когда ноз двух дробей равен произведению знаменателей?
Как минимум, когда знаменатели будут простыми числами, т.е. в качестве примера, это выше приведенные дроби со знаменателями 2 и 3. Эти числа являются простыми, т.е. делятся на себя и на 1.
И общий знаменатель двух чисел 2 и 3 будет равен произведению 2 * 3 = 6.
Формула общего знаменателя
Как вы знаете. что если умножить и числитель и знаменатель на одно число, то результат дроби не изменится! Поэтому мы можем вывести формулу общего знаменателя буквами :
Первую дробь умножаем на знаменатель второй дроби.
А вторую дробь умножаем на знаменатель первой дроби
A B + C D =
A*D B*D + C*B D*B =
A*D + C*B DB
Нахождение общего знаменателя с помощью нок.
Для того чтобы найти общий знаменатель, можно воспользоваться правилом «НОК» для двух чисел, которые здесь — знаменатели.
Если вы не сходили по ссылке, то давайте вкратце попробуем разобраться в формуле подбора общего знаменателя.
Пример нахождения общего знаменателя методом разложения на множители
Это тоже самое. что и выше приведенный «НОК» — только может называться по другому…
смайлы
Этот способ может называться как «нахождение общего знаменателя методом разложения на множители»
Либо «метод нахождения наименьшего общего знаменателя» или просто «НОЗ»
Рассмотрим два знаменателя 8 и 6, к примеру это могут быть две дроби 1/8 и 1/6 и нам нужно найти их общий знаменатель.
Надо расположить в первую строчку наибольший знаменатель — это 8 и разложить его на множители:
8 = 2 * 2 * 2
Ниже раскладываем меньший знаменатель :
6 = 2 * 3
Далее нам нужно исключить все множители, которые повторяются в меньшем знаменателе… это 2 и у нас остается 3. далее эту тройку надо умножить на больший знаменатель :
8 * 3 = 24
Итого получаем общий знаменатель = 24.
Пример номер 2 подбора общего знаменателя
Чтобы у вас не возникало сомнений, давайте разберем второй пример подбора общего знаменателя, пусть это будут 4 и 10.
Берем больший знаменатель раскладываем его на множители :
10 = 2 * 5
Раскладываем меньший знаменатель :
4 = 2 * 2
Виртуально исключаем повторяющиеся множители из второго знаменателя — это 2. И во втором знаменателе остается вторая 2. Умножаем больший знаменатель на 2 :
10 * 2 = 20
Итого получаем общий знаменатель 20, двух чисел 4 и 10.
Как найти общий знаменатель дробей онлайн
У нас есть калькулятор, который в том числе умеет находить общий знаменатель дробей онлайн!
Прежде чем приступать к поиску общего знаменателя, давайте найдем общий знаменатель для двух знаменателей, а потом проверим данное решение на калькуляторе.
Пусть это будут два знаменателя 20 и 6.
Раскладываем больший знаменатель на множители :
20 = 2 * 2 * 5
Раскладываем на множители второй знаменатель :
8 = 2 * 2 * 2
Исключаем повторяющиеся множители во втором знаменателе и у нас остается одна двойка.
Умножаем больший знаменатель на 2 :
20 * 2 = 40
Итого получаем их общий знаменатель 40.
Переходим к нахождению общего знаменателя онлайн
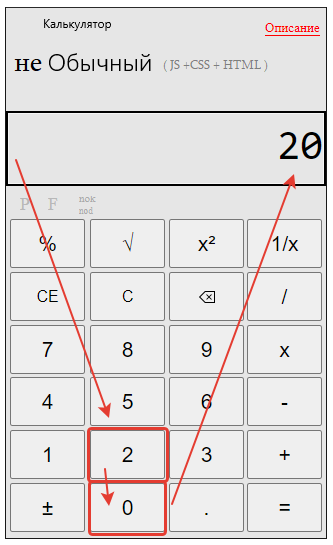
Открываем наш калькулятор.
Вводим первый знаменатель 20.
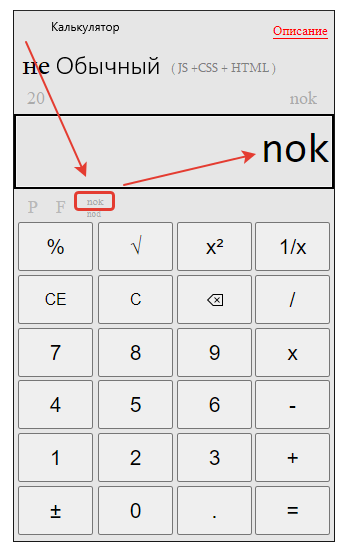
Нажимаем кнопку «НОК»
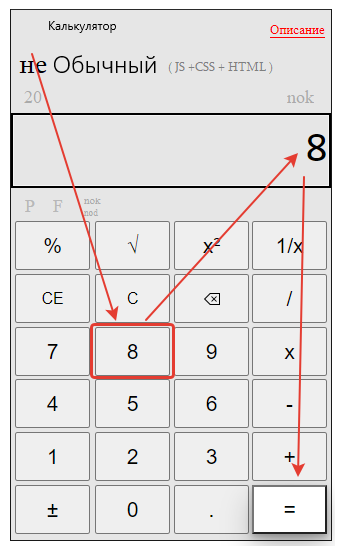
Набираем второй знаменатель 8.
Нажимаем равно — «=»
Получаем результат нахождения общего знаменателя онлайн :

Далее вы можете сравнить два результата нахождения общего знаменателя.
Что такое наименьший общий знаменатель?
Разница между «общим знаменателем«(1) и «наименьшим общим знаменателем«(2) в том, что первое может быть бесконечное количество… а второе «НОЗ», только один!
Но, что же такое «наименьший общий знаменатель»
НОЗ — это абсолютно тоже самое, что и «НОК».
Определение, что же такое «наименьший общий знаменатель»
Наименьший общий знаменатель двух знаменателей — это самое маленькое целое число, которое делится без остатка на первый и второй знаменатель.
Формула наименьшего общего кратного
Для нахождения «наименьшего общего знаменателя» двух знаменателей, нужно эти два знаменателя разложить на множители. Больший знаменатель записываем в первую строчку, второй знаменатель раскладываем на множители и записываем во вторую строчку.
Сравниваем две строки и удаляем из второй все цифры, которые повторяются в первой строчке.
То число(если больше 1, то перемножаем между собой) умножаем на большее число.
Для понимания формулы наименьшего общего кратного нам нужен пример!
Предположим, что у нас есть два знаменателя 10 и 6 и нужно найти наименьший общий знаменатель :
Разложим больший знаменатель на множители :
10 = 2 * 5
Разложим второй знаменатель на множители :
6 = 2 * 3
Теперь, нам нужно исключить повторяющеюся цифру 2 из второй строчки, остается цифра 3.
Умножаем больший знаменатель на 3.
10 * 3 = 30
Итого получаем, что наименьший общий знаменатель двух знаменателей 10 и 5 равно 30.
Как найти наименьший общий знаменатель на калькуляторе
Для понимания процесса получения наименьшего общего знаменателя на калькуляторе нам потребуются два знаменателя, например 18 и 12 из дробей 1/18 и 1/12
Прежде чем приступать к нахождению «нок» двух чисел на калькуляторе, давайте найдем наименьшее общее кратное, как мы делали это выше :
Раскладываем большее число на множители :
18 = 2 * 3 * 3
Раскладываем меньшее число на множители :
12 = 2 * 2 * 3
Исключаем повторяющиеся цифры — это одна 2 и 3, остается 2.
Умножаем большее число на 2.
18 * 2 = 36
Итого получаем, что наименьшее общее кратное двух чисел 18 и 12 = 36.
Теперь проверим правильность нахождения «нок» на калькуляторе.
Открываем калькулятор.
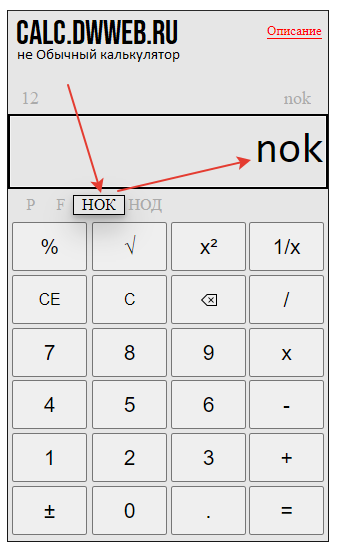
Набираем первое число – пусть это будет число 12
Нажимаем «нок» на калькуляторе – для этого есть специальная кнопка.
После нажатия на кнопку нок – нам нужно добавить втрое число –пусть это будет 18.
И нам отсеется нажать кнопку равно!
И видим результат нахождения наименьшего общего кратного на калькуляторе…
Как найти общий знаменатель трех дробей
Для того чтобы найти общий знаменатель сразу трех дробей нужно подряд найти нок между этими тремя знаменателями!
Для подтверждения данного тезиса — давайте решим задачку/пример.
Задача/пример найдите общий знаменатель для трех дробей.
У нас даны три дроби и у них у всех три разных знаменателя :
Для такой простой задачи можно в уме посчитать… перебором…, а потом подтвердим наше решение через «НОК».
5 — не подходит — не делится на 3.
10 — не подходит — не делится на 3.
15 — не подходит, не делится на 2.
20 — не подходит, не делится на 3.
25 — не подходит, не делится на 2.
30 — подходит
, делится на все без остатка… мы нашли общий знаменатель для трех дробей, методом перебора
Найдем общий знаменатель для трех дробей на калькуляторе через НОК.
Набираем первый знаменатель — 2.
Нажимаем кнопку — «НОК».
Набираем второй знаменатель — 3.
Нажимаем равно — «=».
Далее опять нажимаем — «НОК».
Набираем третий знаменатель — 6.
Нажимаем равно — «=».
Получаем общий знаменатель для трех дробей посчитанный онлайн на калькуляторе.
Как найти общий знаменатель дробей с разными знаменателями
Если говориться о том, чтобы найти общий знаменатель, то логично предположить, что у дробей изначально разные знаменатели — иначе, зачем искать общий знаменатель — ведь знаменатели одинаковые.
Выше были рассмотрены варианты нахождения общего знаменателя дробей с разными знаменателями.
Вариант разложения знаменателей на множители.
Вариант нахождения общего знаменателя с помощью НОК и т.д
Нахождение наименьшего общего знаменателя бывает нужно для сложения, вычитания и сравнения дробей.
Наименьший общий знаменатель – это наименьшее число, которое нацело делится и на первый, и на второй знаменатель двух дробей.
Правило нахождения наименьшего знаменателя следующее:
Для того, чтобы найти наименьший общий знаменатель двух дробей, нужно найти методом подбора наименьшее общее число, которое бы делилось и на первый, и на второй знаменатель. После этого нужно умножить каждую дробь на такое число, чтобы в знаменателе этих дробей получилось найденное нами наименьшее общее число.
Найти наименьший общий знаменатель двух дробей: 56frac{5}{6} и 34frac{3}{4}.
Решение
Находим методом подбора такое наименьшее число, которое нацело делилось бы и на 6, и на 4. Это число 12. Далее умножаем каждую дробь на такие числа, чтобы в знаменателе получилось 12. Первую дробь умножаем на 2, а вторую на 3:
56=5⋅26⋅2=1012frac{5}{6}=frac{5cdot2}{6cdot2}=frac{10}{12}
34=3⋅34⋅3=912frac{3}{4}=frac{3cdot3}{4cdot3}=frac{9}{12}
Дроби приведены к наименьшему общему знаменателю: 12.
Ответ
12
Найти наименьший общий знаменатель двух дробей: 521frac{5}{21} и 27frac{2}{7}.
Решение
Находим методом подбора такое наименьшее число, которое нацело делилось бы и на 21, и на 7. В этом случае это – один из знаменателей, число 21. Далее нужно умножить вторую дробь на такое число, чтобы в знаменателе получилось 21. Умножаем вторую дробь на 3:
27=2⋅37⋅3=621frac{2}{7}=frac{2cdot3}{7cdot3}=frac{6}{21}
Дроби приведены к наименьшему общему знаменателю: 21.
Ответ
21
Решение задач по алгебре онлайн от экспертов Студворк!
Тест по теме “Наименьший общий знаменатель”