Как найти наибольшую абциссу точки - Avtoru.top

Рассмотрим задания, в которых дан график производной функции и требуется найти, в какой точке данного отрезка эта функция принимает наибольшее значение.

№1

На рисунке изображён график производной функции f(x), определённой на интервале (-14;8). В какой точке отрезка [-11;-8] функция f(x) принимает наибольшее значение?

Решение:

Выделяем отрезок [-11;-8].

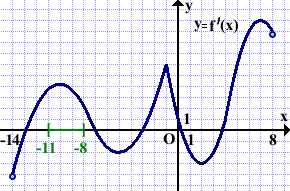
На этом отрезке производная f'(x) принимает положительные значения.

Следовательно, функция f(x) на этом отрезке возрастает, то есть бо́льшему значению аргумента соответствует бо́льшее значение функции:

x₁,x₂ ∈[-11;-8], x₂>x₁, ⇒ f(x₂)>f(x₁).

Поэтому наибольшее значение функция f(x) на отрезке принимает при наибольшем значении аргумента, то есть на правом конце отрезка, при x=-8.

Ответ: -8.

№2

На рисунке изображён график производной функции f(x), определённой на интервале (-7;9). В какой точке отрезка [4;8] функция f(x) принимает наибольшее значение?

Решение:

Выделяем отрезок [4;8].

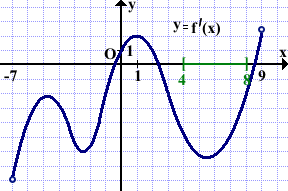
Так как этом отрезке производная f'(x)<o, то функция f(x) на [4;8] убывает, то есть бо́льшему значению аргумента соответствует меньшее значение функции:

x₁,x₂ ∈[4;8], x₂>x₁, ⇒ f(x₂)<f(x₁).

Поэтому наибольшее значение f(x) принимает в этом случае при наименьшем значении аргумента, то есть на левом конце отрезка, при x=4.

Ответ: 4.

№3

Функция y=f(x) определена на промежутке (-5;9). На рисунке изображён график её производной. Найти абсциссу точки, в которой функция y=f(x) принимает наибольшее значение.

Решение:

В точке с абсциссой x=6 производная меняет знак с плюса на минус.

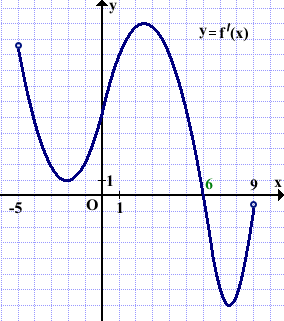
Следовательно, x=6 — точка максимума.

Производная f'(x) существует на всём интервале (-5;9), следовательно, функция f(x) непрерывна на (-5;9).

Если непрерывная функция f(x) имеет на заданном интервале (a;b) только одну точку экстремума x_o и это точка максимума, то на (a;b) функция принимает своё наибольшее значение в точке x_o.

Таким образом, функция f(x) на интервале (-5;9) принимает наибольшее значение в точке x=6.

Ответ: 6.

№4

Функция y=f(x) определена и непрерывна на отрезке [-1;9]. На рисунке изображён график её производной. Найти точку x_o, в которой функция принимает наибольшее значение, если f(-1)≥f(9).

Решение:

На промежутках (-1;3) и (8;9) производная f'(x)>0, поэтому на этих промежутках функция f(x) возрастает.

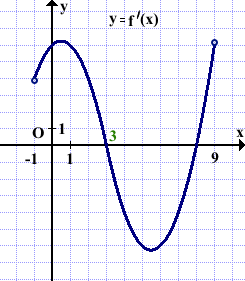
На промежутке (3;9) производная f'(x)<0, поэтому на (3;9) функция f(x) убывает.

Так как функция определена и непрерывна на отрезке [-1;9], то точки -1, 3, 8 и 9 можно включать в промежутки монотонности.

Следовательно, на отрезках [-1;3] и [8;9] функция f(x) возрастает, на отрезке [3;8] — убывает.

На промежутках возрастания наибольшее значение функция принимает на правом конце отрезка. На [-1;3] наибольшее значение f(x) принимает в точке x=3 (точке максимума), на [8;9] — в точке x=9.

Так как на [-1;3] f(x) возрастает, то f(3)>f(-1). По условию, f(-1)≥f(9), значит f(3)>f(9).

Таким образом, наибольшее значение функции f(x) принимает в точке x=3.

Ответ: 3.

Источник

Где абсцисс и ординат?

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо. Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек).

Почему называется ось абсцисс?

Оси декартовой системы Ось х имеет название оси абсцисс. Название это происходит от латинского «отрезок».

Что такое абсцисса функции?

Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X в прямоугольной системе координат (рис. 1).

Как найти ординату точки?

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат. Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А».

Как выглядит прямоугольная система координат?

Прямоугольная система координат обозначается Oxy O x y . Координатными осями называют Ох и Оу , называемые соответственно ось абсцисс и ось ординат.

Что такое ордината простыми словами?

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см.

Что такое ось абсцисс простыми словами?

АБСЦИССА, в математике — расстояние от точки до оси у В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ. Эта величина является х-координатой в паре (х, у), которая определяет местоположение точки на плоскости.

Что такое абсцисса пример?

Абсцисса (от лат. abscindere — отрезать) — отсеченная, одна из трех координат, определяющих положение точки в пространстве. Положим, в частности, что рассматриваемая точка M находится на плоской кривой AMB, отнесенной к двум осям ОХ в OY. АБСЦИССА ж.

Как записываются координаты функции?

Положительные абсциссы обычно располагаются на оси XX’ справа от начала координат; положительные ординаты – вверх по оси YY’ от начала координат. На рис. 1 видно: точка M имеет абсциссу x = 2 и ординату y = 3; точка K имеет абсциссу x = — 4 и ординату y = — 2.5. Это можно записать так: M ( 2, 3 ), K ( — 4, — 2.5 ).

Чему равны абсциссы точек лежащих на оси координат?

1) Все точки, лежащие на оси x (абсцисс) имеют равные нулю ординаты (y=0); 2) Все точки, лежащие на оси y (ординат) имеют равные нулю абсциссы (x=0);

Что значит найти абсциссу точки?

Абсциссой (лат. abscissa — отрезок) точки A называется координата этой точки на оси X’X в прямоугольной системе координат. Величина абсциссы точки A равна длине отрезка OB (см. рисунок).

Сколько координат имеет точка в декартовой системе координат?

Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.

Сколько систем координат?

Горизонтальные системы координат отвечают за размещение объектов на поверхности Земли, а вертикальные определяют локализацию относительных высот и глубин объектов. Существует три типа горизонтальных систем координат – географические, системы координат проекции и местные.

Что такое оси ординат?

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. … В прямоугольной системе координат ось Y’Y называется «осью ординат». При построении графиков функций, ось ординат обычно используется как область значений функции.

Что такое ось абсцисс в математике?

АБСЦИССА, в математике — расстояние от точки до оси у В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ. Эта величина является х-координатой в паре (х, у), которая определяет местоположение точки на плоскости.

Что называется ординатой точки?

Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см.

Как правильно записать координаты точек?

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Источник

Задача 39606 Найдите абсциссу точки максимума функции…

Условие

Найдите абсциссу точки максимума функции y=sqrt(4-4x-x^2)

математика 10-11 класс
8591

Решение

★

Максимум будет в точке, в которой функция под корнем принимает наибольшее значение.
Под корнем квадратичная функция.
Она принимает наибольшее значение в вершине.
Абсцисса вершины

x_(o)=[m]frac{-b}{2a}[/m]

a=-1
b=-4

x_(o)=[m]frac{4}{2cdot (-1)}=-2[/m]

О т в е т. х=-2

Если нужно с обоснованием, то можно вычислить производную и приравнять к 0

А если просто тест, то не надо терять время на нахождение производной и расстановку знака, поэтому см. первый способ

По формуле:

[m](sqrt{u})`=frac{1}{2sqrt{u}}cdot u`[/m]

[m]y`=frac{1}{2sqrt{4-4x-x^{2}}}cdot(4-4x-x^{2})`=frac{-4-2x}{2sqrt{-4-4x-x^{2}}}
[/m]

y`=0

-4-2x=0

x=-2

При переходе через точку х=-2 производная меняет знак с + на —

значит это точка максимума

О т в е т. -2

Написать комментарий

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Тема 10.

Задачи на свойства графиков функций

Комбинации нескольких графиков

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

задачи на свойства графиков функций

Решаем задачи

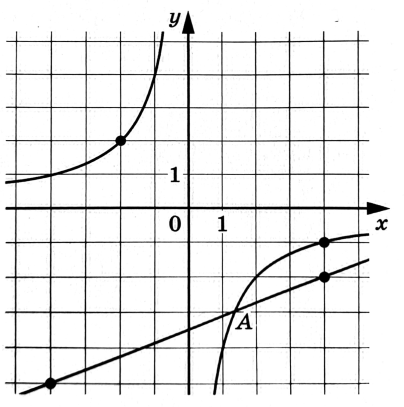
На рисунке изображены графики двух линейных функций, пересекающиеся в точке Найдите абсциссу точки

Показать ответ и решение

Найдем уравнения прямых.

Определим коэффициенты и для нижней прямой. Найдём как тангенс угла наклона прямой:

Δy 0− (−2) 2
k = Δx-= 0−-(−1) = 1 = 2

Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом Подставим точку

Значит, первая функция имеет вид

Теперь определим коэффициенты и для верхней прямой. Найдём как тангенс угла наклона прямой:

Δy 4 − 0 4
k = Δx-= 0−-(−4) = 4 = 1

Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом Подставим точку

Значит, вторая функция имеет вид

Теперь найдем абсциссу точки пересечения двух прямых.

На рисунке изображены графики двух линейных функций, пересекающиеся в точке Найдите абсциссу точки

Показать ответ и решение

Найдем уравнения прямых.

Определим коэффициенты и для нижней прямой. Найдём как тангенс угла наклона прямой:

Δy 2 − 0 2
k = Δx-= 1-− 0 = 1 = 2

Чтобы найти подставим одну из точек на прямой в уравнение с уже рассчитанным коэффициентом Подставим точку
(1;2) :

Значит, первая функция имеет вид

Теперь определим коэффициенты и для верхней прямой. Найдём как тангенс угла наклона прямой:

Δy- -3-− 0- 3
k = Δx = 0− (−3) = 3 = 1

Чтобы найти подставим одну из точек на прямой в уравнение с уже расcчитанным коэффициентом Подставим точку

Значит, вторая функция имеет вид

Теперь найдем абсциссу точки пересечения двух прямых.

На рисунке изображены графики двух линейных функций. Найдите ординату
точки пересечения графиков.

xy110

Показать ответ и решение

Способ 1

Найдём уравнение функции график которой из себя представляет убывающую прямую, на которой отмечены
точки (1;4), Найдём угловой коэффициент:

k = Δy-= −2-− 4-= −1,5
Δx 5− 1

Получим уравнение функции

Найдём значение подставив в уравнение точку (1;4):

Получится уравнение

Найдём уравнение функции график которой из себя представляет возрастающую прямую, на которой
отмечены точки (1;2). Найдём угловой коэффициент:

Δg 2− (−5)
k = Δx-= 1−-(−1) = 3,5

Получим уравнение функции

Найдём значение подставив в уравнение точку (1;2):

Получится уравнение

Теперь решим уравнение

Тогда ордината точки пересечения прямых равна

Способ 2

По картинке видим, что целые точки (1;4) и принадлежат графику первой прямой поэтому можем
составить систему из двух уравнений:

( (
{ 4= f1(1) {4 =k1+ b1
( ⇔ ( ⇔
−2(=f1(5) − 2= 5k1+b(1
{ k1 = 4− b1 { b1 = 5,5
⇔ ( ⇔ (
−2 =5(4− b1)+b1 k1 = −1,5

Также целые точки (1;2) и принадлежат графику второй прямой поэтому можем составить
систему из двух уравнений:

( (
{ 2= f2(1) { 2= k2+ b2
( −5 =f2(−1) ⇔ ( −5= − k2 +b2 ⇔
( (
{ k2 = 2− b2 {b2 = −1,5
⇔ ( ⇔ (
−5= − (2 − b2)+ b2 k2 = 3,5

Значит, функции имеют вид и Аналогично первому способу решаем уравнение
и получаем ответ.

На рисунке изображены графики двух функций вида которые
пересекаются в точке Найдите x0.

xy110

Показать ответ и решение

Первый способ.

Пусть — уравнение первой прямой, — уравнение второй прямой.

Заметим, что первая прямая проходит через точки и Если прямая проходит через точку на плоскости, то
координаты этой точки обращают уравнение этой прямой в верное равенство. Тогда мы получаем систему из двух
уравнений:

( ( ( (
{ 4= k1⋅(−1)+ b1 {4 =− k1+ b1 { b1 = 4+ k1 { b1 = 9
⇔ ⇔ ⇔ 2
( 3= k1⋅(−3)+ b1 (1 =2k1 ( k1 = 12 ( k1 = 12

Значит, — уравнение первой прямой. Вторая прямая проходит через точки и Следовательно, мы
можем получить следующую систему:

( ( ( (
{− 1= k2⋅2+ b2 {− 1= 2k2+ b2 { b2 = −(2k2+ 1) { b2 = −3
( ⇔ ( ⇔ ( ⇔ (
− 4= k2⋅(−1)+ b2 3 =3k2 k2 = 1 k2 = 1

Значит, — уравнение второй прямой. Обе прямые проходят через точку по условию, тогда мы имеем
систему:

(
{ y0 = x02+9 ⇒ x − 3= x0-+9 ⇔ 2x − 6= x + 9 ⇔ x = 15
( y0 = x0− 3 0 2 0 0 0

Второй способ.

Если прямая на плоскости проходит через две точки и то мы можем составить ее каноническое
уравнение:

x− x1 y− y1
a: x2−-x1 = y2−-y1

На рисунке видно, что одна из прямых проходит через точки и Тогда мы можем записать ее каноническое
уравнение:

Другая прямая проходит через точки и . Аналогично запишем ее каноническое уравнение:

Если прямая проходит через точку на плоскости, то координаты этой точки обращают уравнение прямой в верное равенство.
Обе прямые проходят через точку по условию, тогда имеем систему:

({ x0+9
y0 = 2 ⇒ x0− 3= x0-+9 ⇔ 2x0− 6= x0+ 9 ⇔ x0 = 15
( y0 = x0− 3 2

Друзья, поздравляем вас с Новым годом! Этот новогодний пробный вариант ЕГЭ подготовлен специально для вас, и, прорешав все задачи правильно, вы можете получить секретный код. Числу, составленному из цифр каждого ответа, соответствует буква в русском алфавите. Тогда правильные ответы ко всем задачам помогут вам составить фразу, которую мы загадали. Введите ее в поле ответа к заданию 19 без пробелов с маленькой буквы.

На рисунке изображены графики функций и которые
пересекаются в точке Найдите абсциссу точки

xy110

Показать ответ и решение

По картинке видим, что точка (4;3) принадлежит графику функции
следовательно,

f(4)= 3 ⇔ a√4-= 3 ⇔
√-
a= 3 ⇒ f(x)= 3 x
2 2

Посмотрим теперь на график функции Это прямая, которой принадлежат
точки и (4;0). Найдем угловой коэффициент:

0−-(−-4) 1
k = 4− (− 4) = 2

Найдем подставив в уравнение точку (4;0) и 1
k = 2 :

1
g(4) = 0 ⇔ 2 ⋅4 +b =0 ⇔
1
b= −2 ⇒ g(x)= 2x − 2

Найдем абсциссу точки приравняв и g :

3√x = 1x− 2 ⇔ 3√x-= x− 4 ⇔
( 2 2 (
{ 9x= (x− 4)2 {− x2+ 17x− 16= 0
( ⇔ ( ⇔
x− 4≥ 0 x ≥ 4
({ x= 1;16
⇔ x =16
( x≥ 4

На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите x0.

xy110A

Показать ответ и решение

Для начала разберемся, какой из графиков какой функции соответствует.

Координата по вершины параболы равна −-(−2) =− 1,
2⋅(−2) 2 что
соответствует правой параболе.

Любую параболу вида 2
g(x)= ax + bx+ c можно представить в виде

Здесь (xB;yB) — координаты ее вершины. По картинке несложно видеть, что
вершина левой параболы имеет координаты значит функция имеет
вид

Также по картинке видно, что в точке -4 функция равна 1. Это условие
можно записать следующим образом:

Теперь мы полностью восстановили функцию она имеет вид

Найдем точки пересечения и g :

Пересечение, соответствующее это точка Тогда координата
точки равна 3.

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите абсциссу точки

xy110A

Показать ответ и решение

Восстановим уравнение функции f(x). По картинке видно, что её график проходит через три целые точки:
и (1;1).

Так как график f(x) проходит через точку то имеем уравнение:

Так как график f(x) проходит через точку (1;1), то имеем уравнение:

f(1)= 1 ⇔ a ⋅12+ b⋅1+ c= 1 ⇔
⇔ a+ b− 4= 1 ⇔ a+ b= 5

Так как график f(x) проходит через точку то имеем уравнение:

Решим систему из двух уравнений:

( (
{ a+ b= 5 { b= 5− a
( 2a− b= 1 ⇔ ( 2a− (5 − a) =1 ⇔
( ( (
{ b= 5− a {b =5 − a {a = 2
⇔ ( ⇔ ( ⇔ (
2a− 5+ a= 1 3a =6 b = 3

Таким образом, мы полностью восстановили уравнение функции f(x):

2
f(x) = 2x +3x − 4

Восстановим уравнение функции g(x). По картинке видно, что её график проходит через целые точки и
Значит, можем составить систему из двух уравнений:

( (
{g(−2)= − 2 ⇔ {− 2k + d= −2 ⇔
(g(−1)= 2 (− k+ d= 2
( ( (
{d = 2k− 2 { k+ 2= 2k− 2 { k = 4
⇔ (d = k+ 2 ⇔ ( d= k+ 2 ⇔ ( d= 6

Таким образом, мы полностью восстановили уравнение функции g(x):

Найдем координаты второй точки пересечения графиков этих функций:

2 2
2x +3x − 4 = 4x + 6 ⇔ 2x − x−⌊10= 0 ⇔
x = −2
⇔ (x+ 2)(2x− 5)= 0 ⇔ ⌈
x = 2,5

Значит, абсцисса точки равна 2,5.

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите ординату точки

xy110A

Показать ответ и решение

По картинке видно, что график функции g(x) проходит через точки (1;2) и (3;4). Если график функции проходит
через определенную точку, то ее координаты обращают уравнение функции в верное равенство. Значит, мы можем составить
систему из трех уравнений:

( ( (
|||g(−1)= 8 ||| a⋅(−1)2+ b⋅(−1)+ c= 8 |||a − b +c = 8
{g(1)= 2 ⇔ { a⋅(1)2 +b ⋅(1)+ c= 2 ⇔ {a +b +c = 2
||| ||| |||
(g(3)= 4 ( a⋅(3)2 +b ⋅(3)+ c= 4 (9a +3b+ c= 4

Из первого уравнения следует, что Тогда, подставив этот результат во второе уравнение, получим:

Подставив и в третье уравнение, получим:

Тогда можем найти

Значит, мы нашли уравнение функции g(x):

По условию функции f(x) и g(x) пересекаются в точках A(3;4) и Тогда координаты точки обращают
уравнения функций f(x) и g(x) в верные равенства:

(
{ f(x0) =y0
( g(x0)= y0 ⇒ f(x0)= g(x0) ⇔

⇔ − 3x0+ 13= x20− 3x0+ 4 ⇔ 9= x20 x⇒⁄=3 x0 = −3
0

Тогда ордината точки равна

На рисунке изображены графики функций

2
f(x)= ax + bx+ c и g(x)= kx+ d

которые пересекаются в точках и Найдите y0.

xy110A

Показать ответ и решение

Заметим, что любую квадратичную функцию можно представить в виде

2
f (x)= a(x− x0) +y0,

где (x0;y0) — координаты вершины параболы. По графику видно, что y0 =1.

Найдём подставив точку в уравнение параболы:

Получим уравнение параболы

Найдём уравнение линейной функции

график которой проходит через точки и (0;3). Найдём значение углового коэффициента

Δg 3 − 0
k = Δx-= 0−-(−1) = 3

Значение коэффициента равно 3, поскольку прямая пересекает ось ординат в точке (0;3).

Получим уравнение функции

Чтобы найти координаты точки надо решить уравнение

−(x+ 2)2 +1 = 3x + 3
2
− x − 4x − 4+ 1= 3x+ 3
x2 +7x +6 = 0
⌊
⌈x =− 1
x =− 6

Первое значение соответствует абсциссе точки тогда второе — абсциссе точки Найдём её ординату, подставив
в уравнение любой из функций. Подставим в

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите ординату точки

xy110

Показать ответ и решение

Определим какой из графиков («верхний» или «нижний») принадлежит функции f(x). Заметим, что
значит, график функции f(x) проходит через точку (0;4), то есть функции f(x) соответствует «верхний»
график.

Восстановим уравнение функции g(x). Заметим, что «нижний» график проходит через точку следовательно
справедливо равенство

2
g(0)= −3 ⇔ a ⋅0 + b⋅0+ c= −3 ⇔ c= − 3

Также график функции g(x) проходит через целые точки и (1;1) , значит, можем составить систему
уравнений:

({ ({ 2
g(−2)= −5 ⇔ a⋅(−2) + b⋅(− 2)+c = −5 ⇔
( g(1) =1 ( a⋅12+ b⋅1+ c= 1
( (
⇔ {4a− 2b− 3= −5 ⇔ {2a− b= − 1 ⇔
(a+ b− 3= 1 (a+ b =4
( ( (
{ b= 2a+ 1 { 2a +1 = 4− a {a = 1
⇔ ( b= 4− a ⇔ ( b= 4− a ⇔ (b = 3

Таким образом, мы полностью восстановили уравнение функции g(x):

2
g(x)= x + 3x− 3

Теперь найдем абциссу второй точки пересечения графиков функций f(x) и g(x) :

2 2 2
2x − 5x+ 4= x + 3x− 3 ⇔ x − 8x+⌊ 7 =0 ⇔
x= 1
⇔ (x− 1)(x − 7) =0 ⇔ ⌈
x= 7

Значит, абсцисса точки равна 7. Тогда ордината точки равна

На рисунке изображены графики функций √ -
f(x) = a x и которые пересекаются в точках и
Найдите y0.

xy110AB

Показать ответ и решение

Найдём уравнение функции g(x). По графику видно, что k = 1, поскольку функция увеличивается на 1 при увеличении
аргумента на 1. Также прямая пересекает ось ординат в точке (0;1), откуда b = 1. Тогда уравнение прямой имеет
вид

Найдём уравнение функции f(x). Подставим точку (4;5) на графике в уравнение функции:

Тогда уравнение корня имеет вид

Найдём координаты точек пересечения графиков, приравняв функции:

Сделаем замену и получим квадратное уравнение:

t2− 2,5t+ 1= 0
2
2t − 5t+ 2= 0
D = 52− 4⋅2⋅2 =52− 42 = 32
5 ±3 1
t= --4- = 2;2

Сделаем обратную замену и получим совокупность

⌊ ⌊
t= 0,5 x = 0,25
⌈t= 2 ⇔ ⌈x = 4

Точке соответствует координата Подставим её в g(x) и получим

На рисунке изображены графики функций √ ----
f(x) =a x− b+ c и
которые пересекаются в точках A(0;1) и Найдите абсциссу точки

xy110A

Показать ответ и решение

Заметим, что область определения функции √ ----
f(x)= a x− b+ c совпадает с
областью определения функции √----
x − b и равна

Из графика видно, что f(x) определена на откуда получаем

Тогда функция примет вид

По графику то есть

Найдем отличную от точку пересечения графиков функций f(x) и
g(x):

pict

Из последней системы получаем x= 8. Тогда абсцисса точки пересечения
графиков равна 8.

На рисунке изображены графики функций и
которые пересекаются в точках и
Найдите xB.

xy110A

Показать ответ и решение

Поскольку f (x) — квадратичная функция, абсцисса вершины ее графика равна
-−(−2) = −0,5.
2 ⋅(− 2)

Тогда по рисунку график функции f(x) — это правая парабола.

Найдём уравнение левой параболы в виде

где — ее вершина. Подставим точку в уравнение
g(x):

Получим

Чтобы найти координаты точки решим уравнение

pict

Значение — это абсцисса точки тогда xB = 3 — это абсцисса
точки

На рисунке изображены графики функций

√ -
f(x) =a x и g(x)= kx+ b,

которые пересекаются в точке Найдите абсциссу точки

xy110

Показать ответ и решение

По картинке видим, что точка (4;3) принадлежит графику функции следовательно,

√-
f(4) = 3 ⇔ a 4= 3 ⇔
⇔ a = 3 ⇒ f(x)= 3√x-
2 2

Посмотрим теперь на график функции По картинке видим, что ему принадлежат точки и (4;0). Найдем угол
наклона

0−-(−4) 1
k = 4− (−4) = 2

Найдем подставив точку (4;0)

g(4)= 0 ⇔ 1 ⋅4+ b= 0 ⇔
2 1
⇔ b= − 2 ⇒ g(x) = 2x− 2

Найдем абсциссу точки приравняв и

3√ - 1 √-
2 x= 2x − 2 ⇔ 3 x= x − 4 ⇔
( (
{9x = (x − 4)2 { −x2+ 17x− 16= 0
⇔ (x − 4 ≥ 0 ⇔ ( x≥ 4 ⇔
(
{x =1;16
⇔ ( ⇔ x = 16
x ≥4

На рисунке изображены графики двух функций: одна из них линейная, другая — вида

√-----
y = a x− x0+ y0

Найдите абсциссу точки пересечения графиков этих функций. Если таких точек несколько, в ответе укажите наименьшую
абсциссу.

xy110

Показать ответ и решение

Для решения найдём уравнения обеих функций, после чего решим уравнение, приравняв эти функции, что и будет означать
пересечение графиков функций.

Найдём уравнение линейной функции. Заметим, что прямая проходит через точки и (3;2). Тогда угловой
коэффициент можно найти по формуле

k = y1−-y0= --2−-0- = 2
x1− x0 3 − (−4) 7

Получим уравнение прямой

y = 2 +b
7

Для нахождения свободного коэффициента подставим произвольную точку на прямой в это уравнение. Подставим точку
(3;2) :

2 8
2 = 7 ⋅3+ b ⇔ b= 7

Получаем уравнение прямой

y = 2 x+ 8
7 7

Найдём уравнение второй функции. Заметим, что график имеет вершину (2;3), из чего можно сделать вывод, что x0 = 2,
y0 = 3. Чтобы найти подставим в полученную функцию координаты точки (3;4), которая находится на
графике.

√ ----
4= a 3− 2+ 3 ⇔ a= 1

Получаем уравнение второй функции

√-----
y = x − 2+ 3

Приравняем полученные функции:

√x-−-2+ 3= 2x + 8
7 7
√x-−-2= 2x− 13 |⋅7
√ ----7 7
7 x− 2= 2x− 13

Возведём в квадрат обе части уравнения, отметив, что правая чать должна быть неотрицательной, то есть

2
49(x− 2)= 4x + 169− 52x
4x2− 101x+ 267= 0
2 2
D = 101 − 4 ⋅4⋅267 = 5929 = 77
101±-77
x1,2 = 8 = 3;22,25

Поскольку решение уравнения существует при , получим единственное решение

На рисунке изображены графики функций и
которые пересекаются в точках и Найдите x0.

xy110A

Показать ответ и решение

Восстановим график функции f(x). Он проходит через точку Значит, можем составить уравнение:

k
f(−3)= −2 ⇔ −3-=− 2 ⇔ k = 6

Значит, f(x) = 6.
x

Восстановим график функции g(x). Он проходит через точку (0;5), следовательно,

Также график g(x) проходит через точку следовательно,

Значит,

Найдем абсциссу точки B :

⌊
-6 2 ⌈x = −2
x = 4x+ 5 ⇔ 4x + 5x− 6= 0 ⇔ x= 0,75 ⇒ x0 = 0,75

На рисунке изображены графики функций

k
f(x)= x и g(x)= ax+ b,

которые пересекаются в точках и Найдите ординату точки

xy110A

Показать ответ и решение

Подставим точку расположенную на графике гиперболы, в функцию f(x):

k
f(−2)= −-2 = 2 ⇔ k = −4

Найдём коэффициент по точкам на графике линейной функции

a = Δy-= −2-− (−5)-= 3
Δx 4− (− 4) 8

Найдём подставив точку

3
− 2= 8 ⋅4+ b ⇔ b= −3,5

Найдём точки пересечения, приравняв f(x) и g(x):

f(x)= g(x)

−4-= 3x− 3,5− 32= 3x2− 28x
x 8 2
3x − 28x+ 32= 0

Решим данное уравнение методом переброски коэффициента. Решим уравнение

По теореме Виета легко находятся корни ′
x1 = 4 и ′
x2 = 24. Тогда у исходного уравнения корни равны

x′1 4 x′2
x1 =-3 = 3 и x2 = 3-= 8

Видно, что точке соответствует координата x1, тогда точке — координата x2. Найдём ординату, подставив в
g(x):

g(8)= 3 ⋅8− 3,5 = −0,5
8

На рисунке изображены графики функций k
f(x) = x и которые пересекаются в точках и
Найдите абсциссу точки

На рисунке изображены графики функций и , которые пересекаются в точках и .
Найдите ординату точки .

На рисунке изображены графики функций

2 √----
f(x)= ax + bx+ c и |g(x)|= k x + r,

которые пересекаются в точках и
Найдите y0.

Показать ответ и решение

Найдем уравнения каждой функции. Пусть ----
g1(x)= k√x+ r, ----
g2(x)= −k√x + r
— функции, задающие второе уравнение условия. Тогда график g2(x) проходит
через точки и , следовательно,

{0 = −k√ −1+-r- {r = 1
−2 =− k√0+-r ⇔ k = 2

Следовательно,

√ -----
|g(x)|= 2 x+ 1

График проходит через точки A,B,C :

( ( 1
|{ 0= a− b+ c |{ a= 35
|( −2= c ⇔ |( b= −3
−4= 9a+ 3b+ c c= −2

Следовательно,

f(x)= 1x2− 5x − 2
3 3

Найдем четвертую точку пересечения, то есть корень уравнения
По картинке можно предположить, что точка — общая для
графиков f(x) и g1(x). Тогда имеем: