Как найти наибольший отрезок средней линии трапеции - Avtoru.top

Трапеция и ее свойства

Т. А. Унегова

Определения:

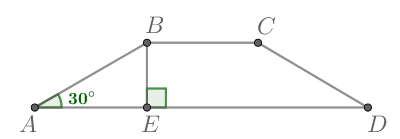
Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

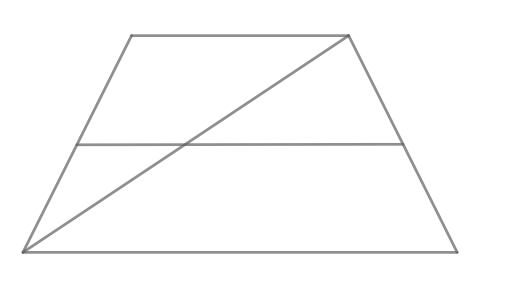
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

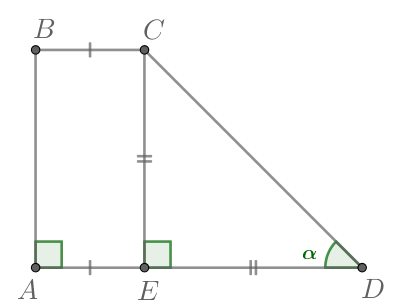
Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: $m=displaystyle frac{a+b}{2}$ .

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: $EF=GH, ; FG=displaystyle frac{a-b}{2}$ .

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN .

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: $S=displaystyle frac{a+b}{2}cdot h$ .

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh .

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: $S=displaystyle frac{1}{2}d_1d_2{sin alpha }$ , где d_1=AC, d_2=BD, (Вместо можно брать

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr . Таким образом, $S=displaystyle frac{a+b+c+d}{2}cdot r$ .

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

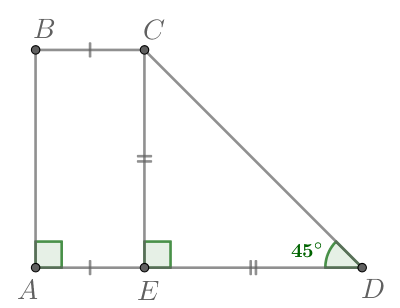
Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2} .

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2 .

Ответ: 2.

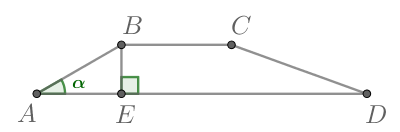
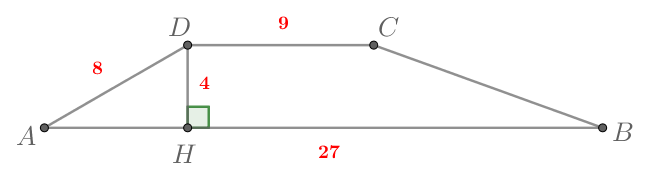
Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ${150}^{{}^circ }$ . Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна ${180}^{{}^circ }$ , и тогда angle BAH $=30{}^circ .$

Из ABH найдем высоту BH. Катет, лежащий против угла в ${30}^{{}^circ }$ , равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна $S=displaystyle frac{6+18}{2}cdot 3,5=42$ .

Ответ: 42.

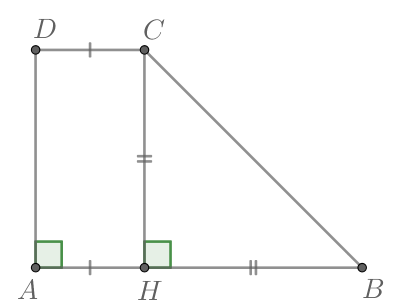
Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть

Периметр трапеции равен

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол $63{}^circ$ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов $vartriangle ACD=3alpha +63{}^circ =180{}^circ$ , откуда
$alpha =39{}^circ .$
Итак, $angle D=78{}^circ$ , а $angle BCD=180{}^circ -78{}^circ =102{}^circ$ .

Ответ: $78{}^circ , 102{}^circ$ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и $h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32.$ Отсюда,

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен ${135}^circ$ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом $45{}^circ$ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна $displaystyle frac{2+4,8}{2}cdot 1,4=4,76$ .

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м ^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции $S=displaystyle frac{a+b}{2}cdot h$ , то $60=displaystyle frac{8+12}{2}cdot h$ , откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.

Решение:

Проведем CE BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что $S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2$ .

Ответ: $displaystyle frac{1}{2}a^2$

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен $60{}^circ$ .

Решение:

По условию задачи в прямоугольном ACD

angle D $=60{}^circ$ , следовательно, angle CAD $=30{}^circ$ .

Так как AC — биссектриса, то angle CAB $=30{}^circ$ , откуда angle DAB $=60{}^circ$ , то есть, трапеция равнобедренная. angle BCA =angle CAD $=30{}^circ$ как накрест лежащие, поэтому ABC — равнобедренный.

Обозначим длины боковых сторон ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в $30{}^circ$ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом $60{}^circ$ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .

Пусть $S_{BCM}$ =S_1 , $S_{ADM}=S_2$ , тогда

$S_2=k^2cdot S_1=36{cdot S}_1.$

Площадь трапеции будет равна

$S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.$

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна $90{}^circ$ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна $90{}^circ$ , то $angle BEC=90{}^circ$ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh , а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то , откуда r=1,2 .

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

откуда

Сторона AB равна диаметру окружности, поэтому r=3 .

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

$m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.$

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна $180{}^circ$ . Она делится на три равные части по $60{}^circ .$

Вписанный угол D опирается на дугу ABC, которая равна $120{}^circ$ , отсюда $angle ADC=60{}^circ$ и, стало быть, $angle C=120{}^circ =angle B.$

Ответ: 120.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Смотрим скрин. Я достроила отрезок АН — параллельный и равный BD. Также достроила отрезок HD- параллельный и равный АВ. Получился параллелограмм ABDH в котором средняя линия равна основанию АВ = 10, а искомый отрезок ЕG = IE = АВ/2 = 10/2 = 5 ед. (условные единицы), потому что треугольники AHD и DBA равны по всем параметрам, и диагональ в параллелограмме делит его среднюю линию пополам.

Мой ответ: Больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей равен 5-ти условным единицам.

автор вопроса выбрал этот ответ лучшим

Знаете ответ?

Источник

Как решать задачи, в которых диагональ трапеции делит ее среднюю линию на отрезки?

Как правило, такие задачи сводятся к рассмотрению двух треугольников.

Задача 1.

Диагональ трапеции делит ее среднюю линию на отрезки длиной c и d. Найти основания трапеции.

Дано: ABCD — трапеция,

AD ∥ BC, MN — средняя линия,

MN∩AC=K, MK=c, KN=d.

Найти: AD, BC.

Решение:

1) Рассмотрим треугольник ACD.

СN=DN и KN ∥ AD (так как по условию MN — средняя линия трапеции).

Следовательно, по теореме Фалеса, AK=KC.

Значит, KN — средняя линия треугольника ACD.

По свойству средней линии треугольника,

$[KN = frac{1}{2}AD, Rightarrow AD = 2KN = 2d.]$

2) Рассмотрим треугольник ABC.

AM=MB (так как MN- средняя линия трапеции), AK=KC (по доказанному). Следовательно, MK — средняя линия треугольника ABC,

$[MK = frac{1}{2}BC, Rightarrow BC = 2MK = 2c.]$

Ответ: 2c, 2d.

Вывод:

Диагональ трапеции делит ее среднюю линию на отрезки, равные половинам оснований.

Задача 2.

Основание AD трапеции ABCD на 6 см больше основания BC, а средняя линия равна 7 см. Найти длины отрезков, на которые диагональ AC делит среднюю линию.

Решение:

Рисунок — как и в задаче 1.

Пусть BC=x см, тогда AD=x+6 см.

По доказанному выше,

$[MK = frac{1}{2}x(cm),KN = frac{1}{2}(x + 6)(cm).]$

$[frac{1}{2}x + frac{1}{2}(x + 6) = 7]$

$[frac{1}{2}x + frac{1}{2}x + 3 = 7]$

$[MK = frac{1}{2} cdot 4 = 2(cm),KN = frac{1}{2}(4 + 6) = 5(cm).]$

Ответ: 2 см, 5 см.

Источник

Тема 1.

Геометрия на плоскости (планиметрия)

Трапеция и ее свойства

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

геометрия на плоскости (планиметрия)

Решаем задачи

Один из углов прямоугольной трапеции равен ∘
113 . Найдите меньший угол этой трапеции. Ответ дайте в градусах.

Показать ответ и решение

В трапеции сумма углов, прилежащих боковой стороне, равна ∘
180 , то есть если один из таких углов равен ∘
113 , то другой
равен

Оставшиеся два угла равны ∘
90 , так как трапеция — прямоугольная. Тогда меньший угол равен ∘
67 .

В трапеции ABCD известно, что ∘
∠BDA = 14 и ∘
∠BDC = 106. Найдите угол ABD. Ответ дайте в
градусах.

Показать ответ и решение

Трапеция равнобедренная, то есть

∘ ∘ ∘
∠BAD = ∠CDA = ∠BDA + ∠BDC = 106 + 14 = 120

По сумме углов треугольника ABD имеем:

∘ ∘ ∘ ∘ ∘
∠ABD = 180 − ∠BAD − ∠ADB = 180 − 120 − 14 = 46

Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.

Показать ответ и решение

Средняя линия трапеции равна полусумме оснований, то есть равна

1 12
2(3 +9)= 2-= 6

Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее
диагоналей.

Показать ответ и решение

Пусть

Так как — средняя линия трапеции, и — средние линии треугольников ADC и ACB соответственно.
Значит,

EO = 1DC = 1⋅10= 5
2 2

1 1
OF = 2 AB = 2 ⋅11 =5,5

Больший из этих отрезков равен 5,5.

Средняя линия трапеции равна 20. Одна из диагоналей трапеции делит среднюю линию в отношении 1 к 4. Найдите большее
основание трапеции.

Основания трапеции равны 6 и 8. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее
диагоналей.

Показать ответ и решение

Для начала найдем длину средней линии трапеции: она равна полусумме оснований, то есть

6+ 8
-2-- =7

Так как — средняя линия трапеции ABCD , то EF ||AB и при этом — середина AD.

Тогда в треугольнике ADB отрезок параллелен основанию и при этом проходит через середину стороны AD.
Значит, — средняя линия треугольника ADB и

EO = 1AB = 4
2

Тогда отрезок равен

Следовательно, наибольший из отрезков средней линии равен 4.

Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции,
прилежащий к данной боковой стороне. Ответ выразите в градусах.

Показать ответ и решение

Опустим высоту на AD. В прямоугольном треугольнике ABE катет напротив угла равен

Запишем площадь трапеции, чтобы найти sinα

1 2SABCD
SABCD = 2(AD + BC )⋅BE ⇒ BE = AD-+-BC-= 4

Тогда

sin α= BE- = 0,5 ⇒ α= 30∘
8

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ∘
150. Найдите
площадь трапеции.

Показать ответ и решение

Пусть ∘
∠ABC =150 , тогда из параллельности ∘
∠DAB = 30 . Опустим высоту на AD. В прямоугольном треугольнике
ABE катет напротив угла в 30∘ равен половине гипотенузы

1
BE = 2AB = 3,5

Тогда площадь трапеции

Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в
градусах.

Показать ответ и решение

Опустим высоту на основание трапеции. ABCE — прямоугольник и Тогда

Запишем площадь трапеции, чтобы найти длину высоты CE :

1 2S 2⋅64
SABCD = 2(BC + AD )⋅CE ⇒ CE = BC-A+BCADD- = 12+-4 = 8

Получили, что Тогда треугольник CDE — прямоугольный с равными катетами, значит, его острый угол
равен 45∘.

Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием
угол 45∘.

Показать ответ и решение

Опустим высоту на основание трапеции. ABCE — прямоугольник и Тогда

Треугольник CDE — прямоугольный с углом в ∘
45 , следовательно, он равнобедренный и Тогда площадь
трапеции

Показать ответ и решение

Рассмотрим треугольники ABC и ACD :

Тогда треугольники ABC и ACD подобны по пропорциональности двух сторон и равенству углов между ними, следовательно,
их площади относятся как квадрат коэффициента подобия:

( )2
SABC-= BC- = 1 ⇒ SACD = 4 ⋅SABC = 8
SACD AC 4

Таким образом,

Основания трапеции равны и боковая сторона равна Площадь трапеции равна 72. Найдите острый угол трапеции,
прилежащий к данной боковой стороне. Ответ дайте в градусах.

Показать ответ и решение

Пусть AD = 8. Проведем

Тогда площадь трапеции равна

AB-+DC-- 27-+9-
72= 2 ⋅DH = 2 ⋅DH ⇒ DH = 4

Рассмотрим прямоугольный △ADH. Так как катет равен половине гипотенузы AD, то угол DAH равен
30∘.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Основания прямоугольной трапеции равны и Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в
градусах.

Показать ответ и решение

Проведем высоту CH.

Тогда ADCH — прямоугольник, следовательно,

Площадь трапеции равна

AB-+-DC- 4+-12
64 = 2 ⋅CH = 2 ⋅CH ⇒ CH =8

Заметим, что мы получили, что Тогда △CHB равнобедренный, значит, углы при основании равны, то есть
Так как сумма острых углов в прямоугольном треугольнике равна 90∘, то

∘ ∘
∠B =∠HBC =90 :2 = 45

Одно из оснований трапеции в 5 раз меньше ее средней линии. Во сколько раз это основание меньше другого основания
трапеции?

Показать ответ и решение

Обозначим меньшее основание трапеции за большее — за Тогда — длина средней линии трапеции. Так как средняя
линия равна полусумме оснований, то

Следовательно, меньшее основание в 9 раз меньше большего основания.

В трапеции боковые стороны равны и 12√5, угол при меньшей боковой стороне равен 135∘. Найдите отношение меньшего
основания к большему, если площадь трапеции равна 156.

Если задача допускает несколько вариантов ответа, внесите в бланк меньший из них.

Показать ответ и решение

Рассмотрим трапецию ABCD, где и проведем в ней высоты и CK. При этом
трапеция может выглядеть двумя разными способами.

1 способ.

Заметим, что △ABH — прямоугольный и равнобедренный, тогда

BH = AH = AB√- = 1√2-= 6√2
2 2

Значит, из прямоугольного △DCK можно найти KD :

√- √ - √-------- √-
KD2 = CD2 − CK2 = (12 5)2− (6 2)2 = 648 ⇒ KD = 9⋅9 ⋅4 ⋅2= 18 2

Т.к. площадь трапеции равна 156 , то имеем следующее уравнение:

√ - √ -
6--2+-18-2+-x+-x ⋅6√2 = 156 ⇒ x =√2
2

Тогда

√- √-
BC :AD = ( 2):(25 2)= 1:25

2 способ.

В этом случае, поступая аналогично первому способу, находим

CK = DK = BH = 6√2-
√ -
AH =18 2
√ - √- √ -
AD = 18 2+ x− 6 2= 12 2+ x

Из уравнения 12√2+ x+ x √-
156 = -----2-----⋅6 2 находим √ -
x =7 2.

Значит,

Т.к. то в ответ пойдет

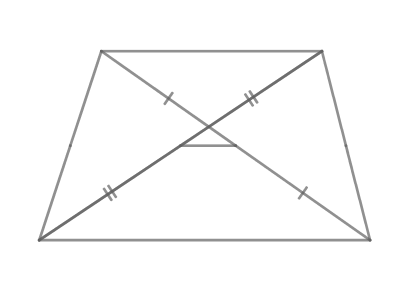
В трапеции ABCD Найдите модуль разности острых углов трапеции.

Показать ответ и решение

△BCD — равнобедренный, следовательно,

∘
∠CBD = ∠CDB =20
∠BAD = 180∘ − ∠ABD − ∠CBD = 180∘− 100∘− 20∘ = 60∘
∘ ∘ ∘
∠ADC = 180 − 140 = 40

Тогда

∘ ∘ ∘ ∘
|∠ADC − ∠BAD |=|40 − 60|= |− 20|= 20

Источник

В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.

Определение средней линии трапеции
Свойства средней линии трапеции
- Свойство 1
- Свойство 2
- Свойство 3
Признак средней линии трапеции
Вторая средняя линия
Пример задачи

Определение средней линии трапеции

Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.

LM – средняя линия трапеции ABCD
L – середина стороны AB, т.е. AL = LB
M – середина стороны CD, т.е. CM = MD

Свойства средней линии трапеции

Свойство 1

Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.

Для рисунка выше:

Свойство 2

Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.

Свойство 3

Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):

Признак средней линии трапеции

Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.

Вторая средняя линия

Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.

Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.

Пример задачи

Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.

Решение

Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = ^(a+b)/₂ ⋅ h

В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = ^(a+b)/₂.

Таким образом, S = m ⋅ h = 25 см ⋅ 7 см = 175 см².

Источник

Трапеция и ее свойства

Теоремы о средней линии и диагоналях трапеции

Теоремы о площади трапеции

Теоремы о вписанных и описанных трапециях

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

Определение средней линии трапеции

Свойства средней линии трапеции

Свойство 1

Свойство 2

Свойство 3

Признак средней линии трапеции

Вторая средняя линия

Пример задачи

Не пропустите также: