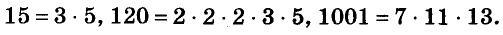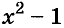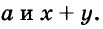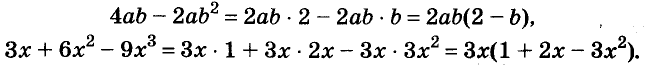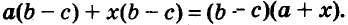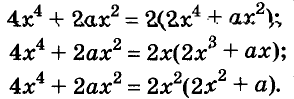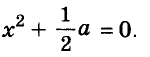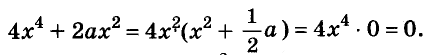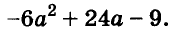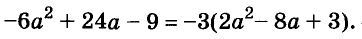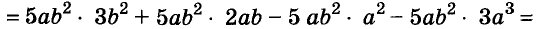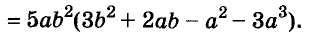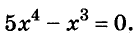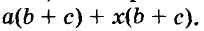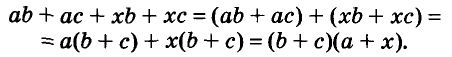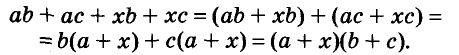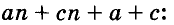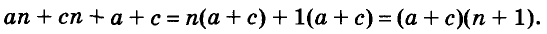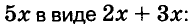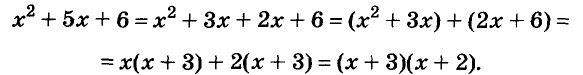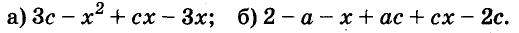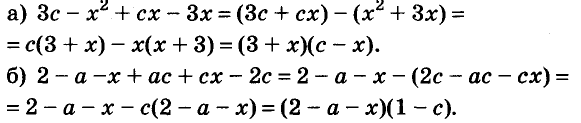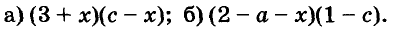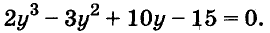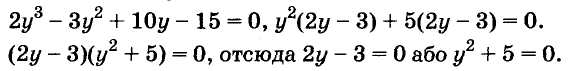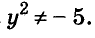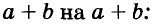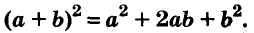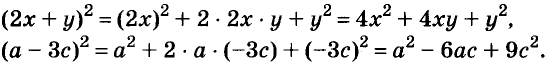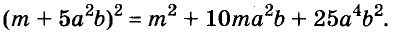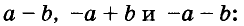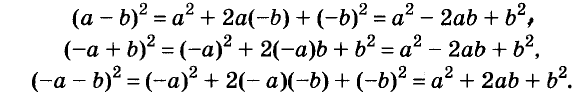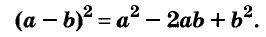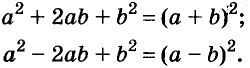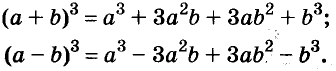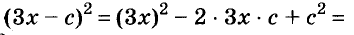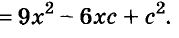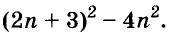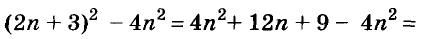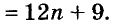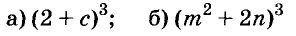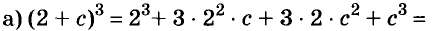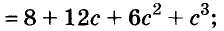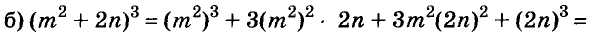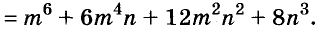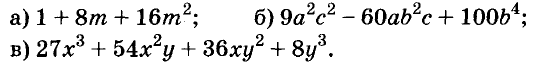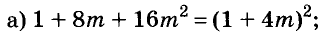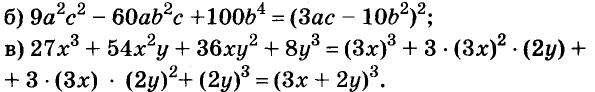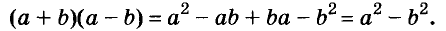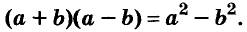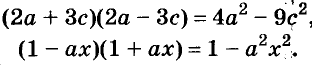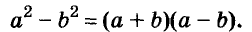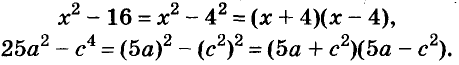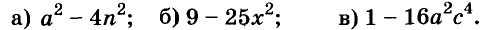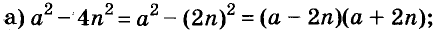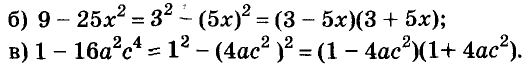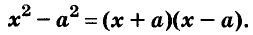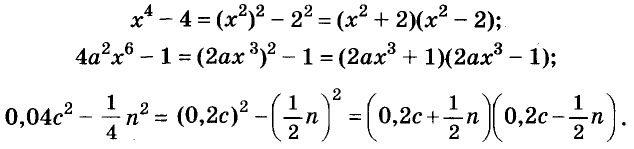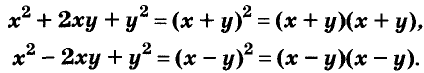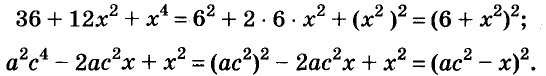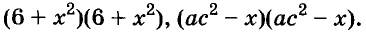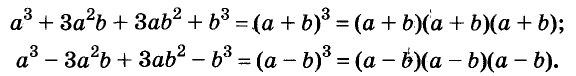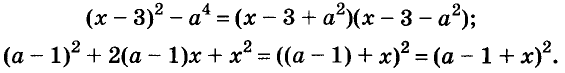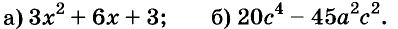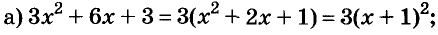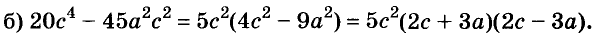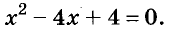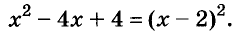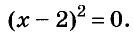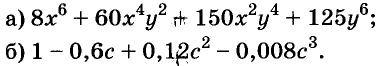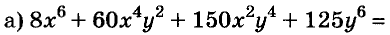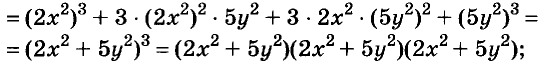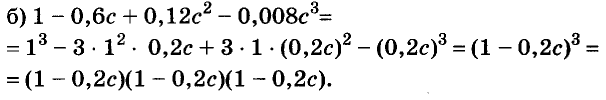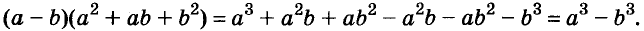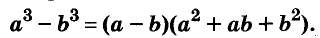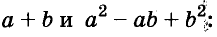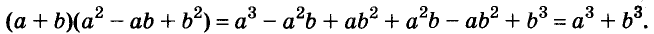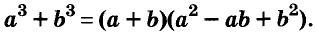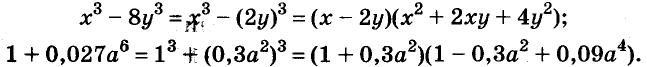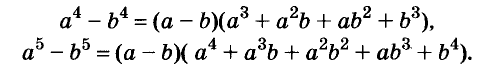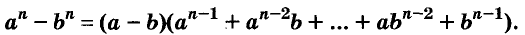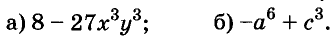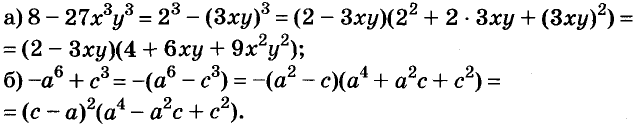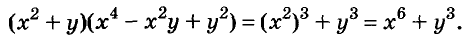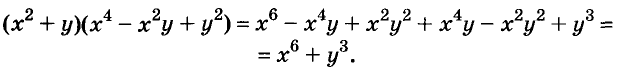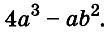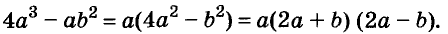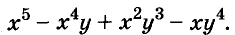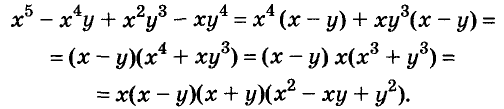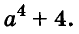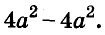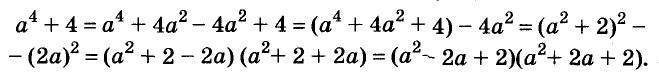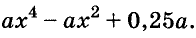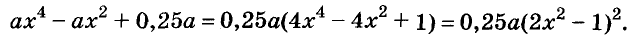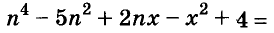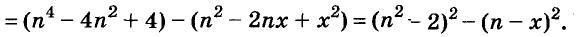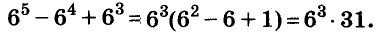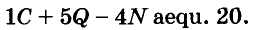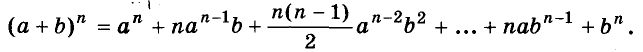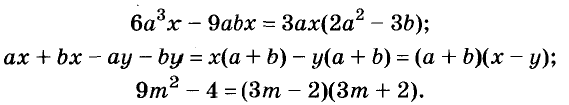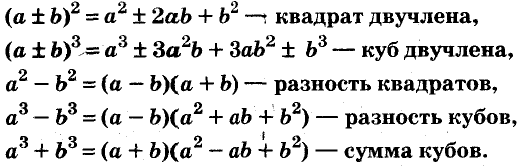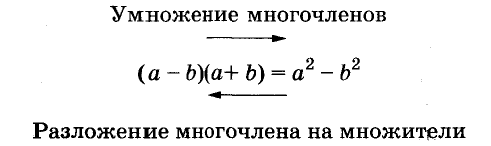Как найти наибольший общий множитель целого выражения

Finding the greatest common factor, or GCF, of two numbers is useful in many situations in math, but particularly when it comes to simplifying fractions. If you’re struggling with this or finding common denominators, learning two methods for finding common factors will help you achieve what you’re setting out to do. First, though, it’s a good idea to learn about the basics of factors; then, you can look at two approaches for finding common factors. Finally, you can look at how to apply your knowledge to simplify a fraction.

What Is a Factor?

Factors are the numbers you multiply together to produce another number. For example, 2 and 3 are factors of 6, because 2 × 3 = 6. Similarly, 3 and 3 are factors of 9, because 3 × 3 = 9. As you may know, prime numbers are numbers that have no factors other than themselves and 1. So 3 is a prime number, because the only two whole numbers (integers) that can multiply together to give 3 as an answer are 3 and 1. In the same way, 7 is a prime number, and so is 13.

Because of this, it’s often helpful to break down a number into “prime factors.” This means finding all of the prime number factors of another number. It basically breaks the number down into its fundamental “building blocks,” which is a useful step towards finding the greatest common factor of two numbers and is also invaluable when it comes to simplifying square roots.

Finding the Greatest Common Factor: Method One

The simplest method for finding the greatest common factor of two numbers is to simply list all of the factors of each number and look for the highest number that both of them share. Imagine that you want to find the highest common factor of 45 and 60. First, look at the different numbers you can multiply together to produce 45.

The easiest way to start is with the two you know will work, even for a prime number. In this case, we know 1 × 45 = 45, so we know 1 and 45 are factors of 45. These are the first and last factors of 45, so you can just fill in from there. Next, work out whether 2 is a factor. This is easy, because any even number will be divisible by 2, and any odd number won’t. So we know that 2 isn’t a factor of 45. What about 3? You should be able to spot that 3 is a factor of 45, because 3 × 15 = 45 (you can always build on what you know to work this out, for example, you’ll know that 3 × 12 = 36, and adding threes to this leads you to 45).

Next, is 4 a factor of 45? No – you know 11 × 4 = 44, so it can’t be! Next, what about 5? This is another easy one, because any number ending in 0 or 5 is divisible by 5. And with this, you can easily spot that 5 × 9 = 45. But 6 is no good because 7 × 6 = 42 and 8 × 6 = 48. From this you can also see that 7 and 8 aren’t factors of 45. We already know 9 is, and it’s easy to see that 10 and 11 aren’t factors. Continue this process, and you’ll spot that 15 is a factor, but nothing else is.

So the factors of 45 are: 1, 3, 5, 9, 15 and 45.

For 60, you run through the exact same process. This time the number is even (so you know 2 is a factor) and divisible by 10 (so 5 and 10 are both factors), which makes things a bit easier. After going through the process again, you should see that the factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.

Comparing the two lists shows that 15 is the greatest common factor of 45 and 60. This method can be time consuming, but it’s simple and it will always work. You can also start at any high common factor you can spot straight away, and then simply look for higher factors of each number.

Finding the Greatest Common Factor: Method Two  

The second method of finding the GCF for two numbers is to use prime factors. The process of prime factorization is a little easier and more structured than finding every factor. Let’s go through the process for 42 and 63.

The process of prime factorization basically involves breaking the number down until you’re only left with prime numbers. It’s best to start with the smallest prime (two) and work from there. So for 42, it’s easy to see that 2 × 21 = 42. Then work from 21: Is 2 a factor? No. Is 3? Yes! 3 × 7 = 21, and 3 and 7 are both prime numbers. This means the prime factors of 42 are 2, 3 and 7. The first “break” used 2 to get to 21, and the second broke this down into 3 and 7. You can check this by multiplying all of your factors together and checking you get the original number: 2 × 3 × 7 = 42.

For 63, 2 isn’t a factor, but 3 is, because 3 × 21 = 63. Again, 21 breaks down into 3 and 7 – both prime – so you know the prime factors! Checking shows that 3 × 3 × 7 = 63, as required.

You find the highest common factor by looking at which prime factors the two numbers have in common. In this case, 42 has 2, 3 and 7, and 63 has 3, 3 and 7. They have 3 and 7 in common. To find the highest common factor, multiply all of the common prime factors together. In this case, 3 × 7 = 21, so 21 is the greatest common factor of 42 and 63.

The previous example can be solved more quickly this way too. Because 45 is divisible by three (3 × 15 = 45), and 15 is also divisible by three (3 × 5 = 15), the prime factors of 45 are 3, 3 and 5. For 60, it’s divisible by two (2 × 30 = 60), 30 is divisible by two as well (2 × 15 = 30), and then you’re left with 15, which we know has three and five as prime factors, leaving 2, 2, 3 and 5. Comparing the two lists, three and five are the common prime factors, so the greatest common factor is 3 × 5 = 15.

In the event that there are three or more common prime factors, you multiply them all together in the same way to find the greatest common factor.

Simplifying Fractions With Common Factors

If you’re presented with a fraction like 32/96, it can make any calculations that come after it very complicated unless you can spot a way to simplify the fraction. Finding the lowest common factor of 32 and 96 will tell you the number to divide both by, to get a simpler fraction. In this case:

32 = 2 × 16 \ 16 = 2 × 2 × 2 × 2 \ text{So } 32 = 2^5 = 2 × 2 × 2 × 2 × 2

For 96, the process gives:

96 = 48 × 2 \ 48 = 24 × 2 \ 24 = 12 × 2 \ 12 = 6 × 2 \ 6 = 3 × 2 \ text{So } 96 = 2^5 × 3 = 2 × 2 × 2 × 2 × 2 × 3

It should be clear that 2⁵ = 32 is the highest common factor. Dividing both parts of the fraction by 32 gives:

frac{32}{96} = frac{1}{3}

Finding common denominators is a similar process. Imagine that you had to add the fractions 15/45 and 40/60. We know from the first example that 15 is the highest common factor of 45 and 60, so we can immediately express them as 5/15 and 10/15. Since 3 × 5 = 15, and both numerators are also divisible by five, we can divide both parts of both fractions by five to get 1 /3 and 2/3. Now they are much easier to add and see that

frac{15}{45} + frac{40}{60} = 1

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

• вынесении общего множителя за скобки;
• способе группировки;
• формулах сокращённого умножения;
• применении разных способов разложения многочленов на множители.

Вынесение общего множителя за скобки

Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 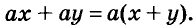Это означает, что данный многочлен ах + ау разложен на два множителя:

Другие примеры:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 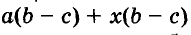общий множитель b — с. Его также можно выносить за скобки:

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 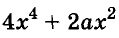при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

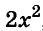
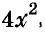
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

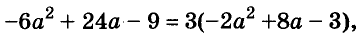
Пример:

Разложите на множители многочлен

Решение:

Пример:

Докажите, что число 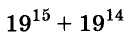делится на 20.

Доказательство:

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

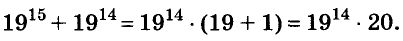
Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

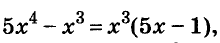
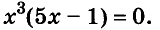
Значит, 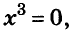отсюда х = 0, или 5х — 1 = 0, отсюда х = 0,2.

Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

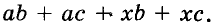
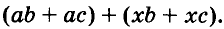
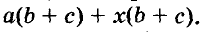
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 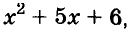• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Ответ. у = 1,5.

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 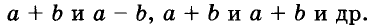Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

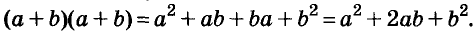
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Запомните формулу

Формулы квадрата двучлена используют и в «обратном направлении»:

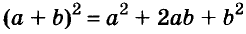
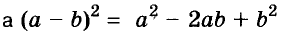
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

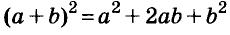
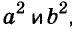
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

• Заказать решение задач по высшей математике

Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 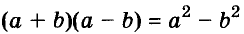можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

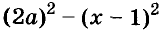
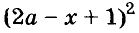
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

.

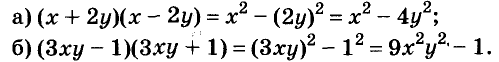
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 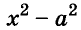можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 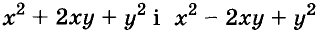раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 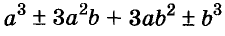можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 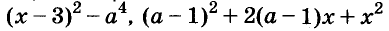— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.

Ответ. х = 2.

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов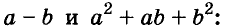

Следовательно, при любых значениях а и b

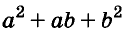
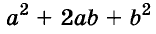
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Следовательно,

Трёхчлен 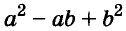называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Если умножить на а — b выражения то получим формулы:

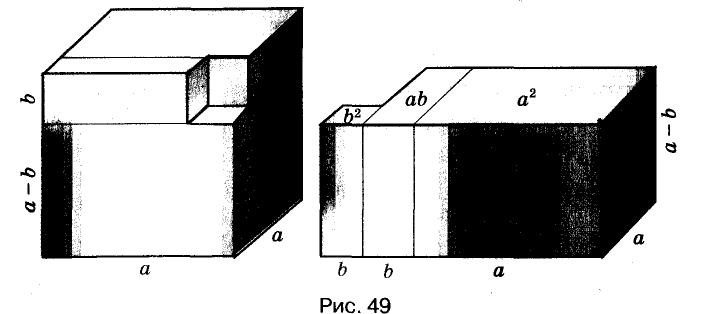
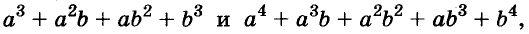
Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •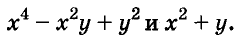

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

1. Вынести общий множитель (если он есть) за скобки.
2. Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
3. Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
4. Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 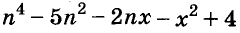в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 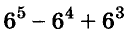делится на 31.

Доказательство:

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

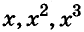
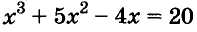
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

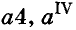
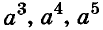
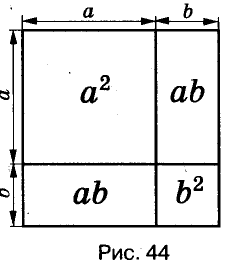
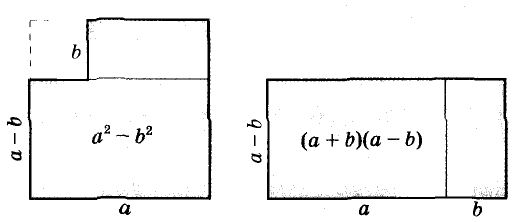
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 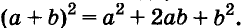Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

• вынесение общего множителя за скобки;
• способ группировки;
• использование формул сокращённого умножения.

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.