Как найти наибольшее значение функции y 4sin - Avtoru.top

Найди верный ответ на вопрос ✅ «Найдите наибольшее значение функции y=4sin x …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Главная » Алгебра » Найдите наибольшее значение функции y=4sin x

Источник

Находим производную y’=4cosx
Приравниваем к нулю чтобы найти критические точки:
4сosx=0 cosx=0 x= p/2 + pn — кр точка

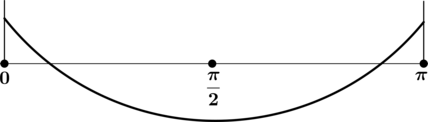
y(p/2)= 4sinp/2= 4 *1= 4

ymax=y(p/2)=4

Комментариев (0)

Ваш ответ

Источник

Онлайн калькулятор для нахождения наибольшего значения функции на отрезке в заданном интервале. Вычислить точки наибольшего значения функции.

Для примера рассмотрим нахождение f(x)=x(x-3)^2 максимального значения точки графика функции на отрезке от -2 до 5. Результат = 20.
Вам может понадобиться калькулятор для нахождения наименьшего значения функции.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник

Тема 11.

Исследование функций с помощью производной

Поиск наибольшего/наименьшего значения у сложных функций

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

исследование функций с помощью производной

Решаем задачи

Найдите наименьшее значение функции

2
y =log3(x + 8x+ 19)

Показать ответ и решение

Выпишем ОДЗ:

1) Обозначим тогда

Найдем производную функции по

Найдём критические точки, то есть внутренние точки области определения
функции, в которых её производная равна 0 или не существует:

1--⋅--2x-+8---= 0 ⇔ 2x+ 8= 0
ln3 x2+ 8x+ 19

Отсюда При этом производная существует всюду на ОДЗ.

Для того, чтобы найти наибольшее/наименьшее значение функции, нужно
понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства и промежутки монотонности y :

3) Эскиз графика y :

Таким образом, наименьшее значение функции достигается в точке
минимума

Найдите наименьшее значение функции

на
отрезке .

Показать ответ и решение

Найдем ОДЗ: — любое число.

1) Найдем производную:

Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна 0 или не существует):

x2− 4
2x ⋅ e = 0 ⇔ x = 0

Таким образом, при x = 0 . Производная существует при любом .

2) Найдём промежутки знакопостоянства и промежутки монотонности :

3) Найдём промежутки знакопостоянства y ′ и промежутки монотонности на отрезке
:

4) Эскиз графика на отрезке :

Таким образом, наименьшего на отрезке значения функция достигает в точке
.

Тогда — наименьшее значение функции на отрезке .

Найдите наименьшее значение функции

на отрезке [0;π].

Показать ответ и решение

Найдем ОДЗ: — любое число.

1) Найдем производную:

′
y = −2⋅sin2x

Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:

πn
− 2⋅sin2x =0 ⇔ 2x = πn, n ∈ℤ ⇔ x= -2-, n ∈ℤ

Производная существует при любом

2) Найдём промежутки знакопостоянства ′
y и промежутки монотонности y :

Здесь бесконечное число промежутков, в которых чередуются знаки производной.

3) Найдём промежутки знакопостоянства и промежутки монотонности на отрезке [0;π]:

4) Эскиз графика на отрезке [0;π]:

Таким образом, наименьшего на отрезке [0;π] значения функция достигает в точке минимума x = π-:
2

( π)
y 2 = cosπ =− 1

Найдите наименьшее значение функции

Показать ответ и решение

Способ 1.

Функцию можно переписать в виде

(x− 7)2+1
y = 4

Эта функция является композицией двух функций: возрастающей y = 4x
1 и
возрастающей при x> 7 и убывающей при x< 7 функции 2
y2 =(x − 7) + 1:

Следовательно, исходная функция возрастает при x > 7 и убывает при x < 7,
то есть x= 7 является точкой минимума.

Следовательно, в этой точке достигается наименьшее значение функции:

P.S. Композиция двух возрастающих или двух убывающих функций —
возрастающая, а возрастающей и убывающей — убывающая.

Способ 2.

Функция определена при всех Исследуем функцию и найдем ее
промежутки возрастания и убывания, для этого найдем ее производную:

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область
определения производной на промежутки, на каждом из которых она непрерывна и
принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков:

PICT

При производная отрицательна, то есть функция
убывает; при производная положительна, то есть функция
возрастает. Следовательно, x= 7 является точкой минимума и наименьшего
значения функция достигает в этой точке:

72−14⋅7+50 1
y(7)= 4 = 4 = 4

Найдите наименьшее значение функции

∘ -----------
f (x)= x4− 4x2+ 13

Показать ответ и решение

Преобразуем исходную функцию:

Заметим, что (2 )2
x − 2 ≥ 0. Значит,

( )2 ∘ -----------
x2− 2 + 9≥ 9 ⇒ (x2− 2)2 +9 ≥ 3 ⇔ f(x) ≥3

Мы доказали, что Значит, если мы докажем, что существует такая точка x = x0, что то 3 будет
наименьшим значением функции f(x).

Для этого найдем точку, в которой

Пусть x =√2,
0 тогда

Значит, наименьшее значение функции f(x) равно 3.

Найдите наименьшее значение функции

2x x
y = e − 8e +9

на отрезке [0;2].

Показать ответ и решение

Найдем критические точки функции 2x x
f(x) =e − 8e + 9. Для этого посчитаем производную:

′ 2x x x x
f (x)= 2 ⋅e − 8e = 2e (e − 4)

Теперь найдем нули производной:

x x x
2e (e − 4)= 0 ⇔ e = 4 ⇔ x = ln4

При этом 2
0 <ln4< lne = 2, то есть данная точка лежит на отрезке [0;2].

Наименьшее значение функции на отрезке достигается в точке экстремума или на концах отрезка. Сравним значения
функции во всех таких точках:

pict

Таким образом, наименьшее значение функции на отрезке [0;2] равно -7.

Найдите наибольшее значение функции

√ - ∘ -----
y = 2⋅ x2+ 1

на отрезке

Показать ответ и решение

Найдем ОДЗ: — любое число.

1) Найдем производную:

√- 2x √ - x
y′ = 2 ⋅-√-2----= 2⋅√--2---
2 x + 1 x + 1

Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:

√2-⋅√--x---= 0 ⇔ x = 0
x2 +1

Производная существует при любом

2) Найдём промежутки знакопостоянства и промежутки монотонности y :

3) Найдём промежутки знакопостоянства и промежутки монотонности на отрезке

4) Эскиз графика на отрезке

Таким образом, наибольшего на отрезке значения функция достигает в точке или в точке x = 1. Сравним
значения функции в этих точках:

√ - √---- √ - √-
y(−1)= 2⋅ 1+ 1 = 2⋅ 2 = 2

√ - √---- √- √ -
y(1)= 2⋅ 1 +1 = 2⋅ 2= 2

Тогда наибольшее значение функции на отрезке равно 2.

Найдите наибольшее значение функции

Показать ответ и решение

1) Обозначим , тогда .

Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):

(так
как , но et > 0 при любом ), откуда находим корень x = 6 . Для того, чтобы
найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её
график.

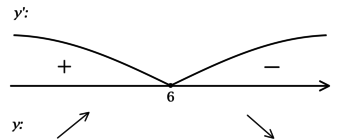
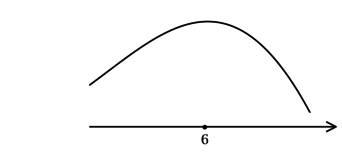
2) Найдём промежутки знакопостоянства ′
y :

3) Эскиз графика:

Таким образом, x = 6 – точка максимума функции и наибольшее значение достигается в
ней:

Итого: − 4 – наибольшее значение функции .

Найдите наибольшее значение функции

2 √ -
y = − log17(2x − 2 2x+ 2)

Показать ответ и решение

Найдем ОДЗ: 2 √ -
2x − 2 2x+ 2 > 0 .

1) Обозначим 2 √-
2x − 2 2x + 2 = t(x) , тогда .

Найдем производную:

′ ′ ′ ′ 2 √ - ′
y = yt ⋅tx = (− log17t) ⋅(2x − 2 2x+ 2) =

√ -
1 1 √ - 1 4x − 2 2
= − ln-17 ⋅-t ⋅(4x− 2 2) = − ln17 ⋅2x2-−-2√2x-+-2

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна
или не существует):

√ -
-1-- ---4x−√2--2--- √ -
− ln17 ⋅2x2 − 2 2x+ 2 = 0 ⇔ 4x− 2 2 = 0

— на ОДЗ, откуда находим корень √ -
x = --2
2 .

Производная функции не существует при 2 √-
2x − 2 2x +2 = 0 , но у данного уравнения отрицательный
дискриминант, следовательно, у него нет решений.

Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её
график.

2) Найдём промежутки знакопостоянства ′
y и промежутки монотонности :

3) Эскиз графика :

Таким образом, наибольшего значение функция достигает в точке √ -
x = --2
2 :

( √-)
y -2- = − log171 = 0
2

Найдите наибольшее значение функции 2x x
y = −e +4e + 3 на отрезке [0;1].

Показать ответ и решение

Найдем критические точки функции 2x x
f(x) =− e +4e + 3. Для этого посчитаем производную:

′ ( 2x) x x x
f(x)= 2⋅ −e + 4e =2e (2− e )

Теперь найдем нули производной:

x x x
2e (2 − e )= 0 ⇔ e = 2 ⇔ x = ln2

При этом то есть данная точка лежит на отрезке [0;1].

Наибольшее значение функции на отрезке достигается в точке экстремума или на концах отрезка. Сравним значения
функции во всех таких точках:

pict

Таким образом, наибольшее значение функции на отрезке [0;1] равно 7.

Найдите наибольшее значение функции

√-
y = ecosx+sinx− 2 .

Показать ответ и решение

1) Обозначим √ --
cos x + sin x − 2 = t(x) , тогда .

√ -- √-
y′ = y′t ⋅ t′x = (et)′ ⋅ (cosx + sin x − 2)′ = et ⋅ (− sin x + cosx ) = ecosx+sin x− 2 ⋅ (− sin x + cosx).

√-
ecosx+sinx− 2 ⋅ (− sin x + cosx ) = 0 ⇔ − sinx + cos x = 0

(так
как √-
ecosx+sinx− 2 = et , но et > 0 при любом ), что равносильно tgx = 1 при , откуда
находим корни x = π-+ πk, k ∈ − ℤ
4 . Для того, чтобы найти наибольшее/наименьшее значение функции,
нужно понять, как схематично выглядит её график.

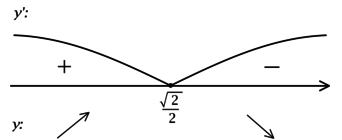
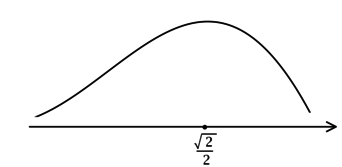
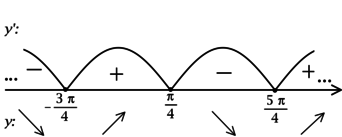
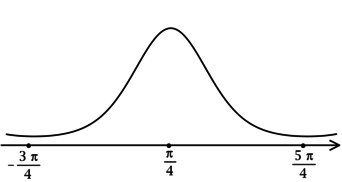
2) Найдём промежутки знакопостоянства : (их бесконечно много, но они чередуются)

3) Эскиз графика:

Таким образом, π
x = 4-+ 2πk, k ∈ ℤ – точки локальных максимумов функции и наибольшее значение
достигается в одной из них:

Итого: – наибольшее значение функции .

Источник

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск наибольшего/наименьшего значения у элементарных функций

(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]), необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]), а также на его концах.

(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)).

(blacktriangleright) Основные формулы поиска производной ((f=f(x), g=g(x)) – функции):

1. Умножение функции на число: [(ccdot f)’=ccdot f’]

2. Сумма или разность двух функций: [(fpm g)’=f’pm
g’]
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

Задание
1

#2341

Уровень задания: Легче ЕГЭ

Найдите наименьшее значение функции (y = x^2).

ОДЗ: (x) – произвольный.

1) [y’ = 2x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

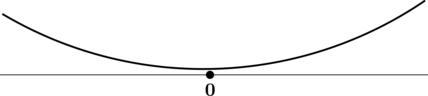
3) Эскиз графика:

Таким образом, наименьшего значения функция достигает в (x = 0).

[y(0) = 0,.] Итого: (0) – наименьшее значение функции (y).

Ответ: 0

Задание
2

#2342

Уровень задания: Равен ЕГЭ

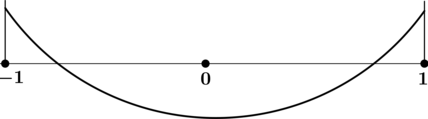
Найдите наибольшее значение функции (y = -2x^2 + 1) на отрезке ([-5; 5]).

ОДЗ: (x) – произвольный.

1) [y’ = -4x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-4x = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-5; 5]):

4) Эскиз графика на отрезке ([-5; 5]):

Таким образом, наибольшего на ([-5; 5]) значения функция достигает в (x = 0).

[y(0) = 1,.] Итого: (1) – наибольшее значение функции (y) на ([-5; 5]).

Ответ: 1

Задание
3

#2343

Уровень задания: Равен ЕГЭ

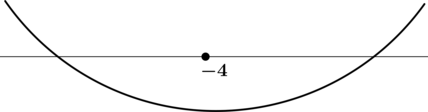
Найдите наименьшее значение функции (y = 2x^2 + 2x + 11) на отрезке ([-4; 0]).

ОДЗ: (x) – произвольный.

1) [y’ = 4x + 2]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [4x + 2 = 0qquadLeftrightarrowqquad x = -0,5,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-4; 0]):

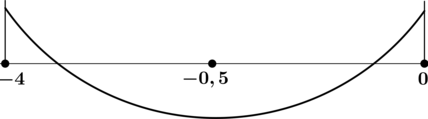
4) Эскиз графика на отрезке ([-4; 0]):

Таким образом, наименьшего на ([-4; 0]) значения функция достигает в (x = -0,5).

[y(-0,5) = 2cdot 0,25 — 1 + 11 = 10,5,.] Итого: (10,5) – наименьшее значение функции (y) на ([-4; 0]).

Ответ: 10,5

Задание
4

#896

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = -x^2 + 21x + 11).

1) (y’ = -2x + 21).

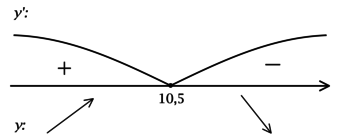
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2x + 21 = 0qquadLeftrightarrowqquad x = 10,5.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

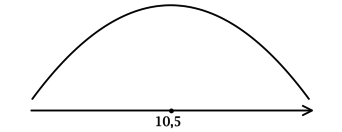
3) Эскиз графика (y):

Таким образом, (x = 10,5) – точка максимума функции (y).
(y(10,5) = -(10,5)^2 + 21cdot 10,5 + 11 = 121,25).
Итого: наибольшее значение функции (y) равно (121,25).

Ответ: 121,25

Задание
5

#897

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции (y = x^2 — 200x + 1).

1) (y’ = 2x — 200).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x — 200 = 0qquadLeftrightarrowqquad x = 100.] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

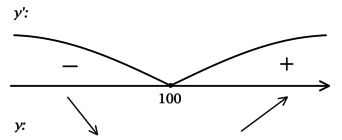
2) Найдём промежутки знакопостоянства (y’):

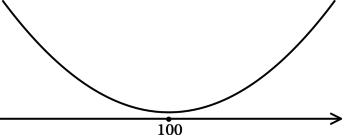
3) Эскиз графика (y):

Таким образом, (x = 100) – точка минимума функции (y).
(y(100) = 100^2 — 200cdot 100 + 1 = -10000 + 1 = -9999).
Итого: наименьшее значение функции (y) равно (-9999).

Ответ: -9999

Задание
6

#3130

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение функции [f(x)=x^3+4x+sin pi x]

на отрезке (left[-dfrac12;dfrac12right].)

Для того, чтобы найти наименьшее значение функции на отрезке, нужно понять, как схематично выглядит график функции на этом отрезке. Для этого найдем производную: [f'(x)=3x^2+4-pi cospi x] Заметим, что (x^2geqslant 0), (-pileqslant picospi xleqslant
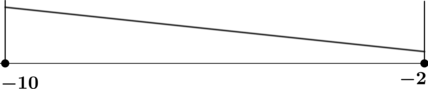
pi), следовательно, [3x^2+4-pi cospi xgeqslant 3cdot 0+4-pi>0] Следовательно, (f'(x)>0) при всех (x), значит, функция (f(x)) возрастает. Следовательно, на отрезке (left[-dfrac12;dfrac12right]) ее график выглядит так:

Следовательно, наименьшее значение функция принимает в точке (x=-frac12): [f_{min}=fleft(-dfrac12right)=-3,125.]

Ответ: -3,125

Задание
7

#898

Уровень задания: Равен ЕГЭ

Найдите наибольшее значение функции (y = x^3 — 15x^2 + 27x + 1032) на отрезке ([0; 10]).

1) (y’ = 3x^2 — 30x + 27).

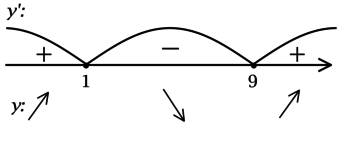
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 — 30x + 27 = 0,] откуда находим корни (x_1 = 1, x_2 = 9). Таким образом, [y’ = 3(x-1)(x-9).] Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

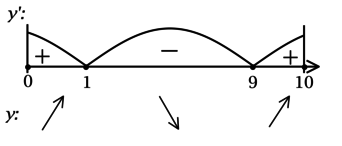
3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([0; 10]):

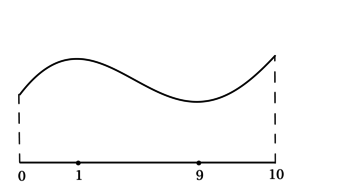
4) Эскиз графика на отрезке ([0; 10]):

Таким образом, (x = 1) – точка локального максимума функции (y) и наибольшее значение на ([0; 10]) функция достигает либо в (x = 1), либо в (x = 10). Сравним эти значения:

(y(1) = 1 — 15 + 27 + 1032 = 1045),

(y(10) = 1000 — 1500 + 270 + 1032 = 802).

Итого: наибольшее значение функции (y) на ([0; 10]) равно (1045).

Ответ: 1045