Как найти наиболее часто встречающееся число

With so many solutions proposed, I’m amazed nobody’s proposed what I’d consider an obvious one (for non-hashable but comparable elements) — [itertools.groupby][1]. itertools offers fast, reusable functionality, and lets you delegate some tricky logic to well-tested standard library components. Consider for example:

import itertools
import operator

def most_common(L):
  # get an iterable of (item, iterable) pairs
  SL = sorted((x, i) for i, x in enumerate(L))
  # print 'SL:', SL
  groups = itertools.groupby(SL, key=operator.itemgetter(0))
  # auxiliary function to get "quality" for an item
  def _auxfun(g):
    item, iterable = g
    count = 0
    min_index = len(L)
    for _, where in iterable:
      count += 1
      min_index = min(min_index, where)
    # print 'item %r, count %r, minind %r' % (item, count, min_index)
    return count, -min_index
  # pick the highest-count/earliest item
  return max(groups, key=_auxfun)[0]

This could be written more concisely, of course, but I’m aiming for maximal clarity. The two print statements can be uncommented to better see the machinery in action; for example, with prints uncommented:

print most_common(['goose', 'duck', 'duck', 'goose'])

emits:

SL: [('duck', 1), ('duck', 2), ('goose', 0), ('goose', 3)]
item 'duck', count 2, minind 1
item 'goose', count 2, minind 0
goose

As you see, SL is a list of pairs, each pair an item followed by the item’s index in the original list (to implement the key condition that, if the «most common» items with the same highest count are > 1, the result must be the earliest-occurring one).

groupby groups by the item only (via operator.itemgetter). The auxiliary function, called once per grouping during the max computation, receives and internally unpacks a group — a tuple with two items (item, iterable) where the iterable’s items are also two-item tuples, (item, original index) [[the items of SL]].

Then the auxiliary function uses a loop to determine both the count of entries in the group’s iterable, and the minimum original index; it returns those as combined «quality key», with the min index sign-changed so the max operation will consider «better» those items that occurred earlier in the original list.

This code could be much simpler if it worried a little less about big-O issues in time and space, e.g….:

def most_common(L):
  groups = itertools.groupby(sorted(L))
  def _auxfun((item, iterable)):
    return len(list(iterable)), -L.index(item)
  return max(groups, key=_auxfun)[0]

same basic idea, just expressed more simply and compactly… but, alas, an extra O(N) auxiliary space (to embody the groups’ iterables to lists) and O(N squared) time (to get the L.index of every item). While premature optimization is the root of all evil in programming, deliberately picking an O(N squared) approach when an O(N log N) one is available just goes too much against the grain of scalability!-)

Finally, for those who prefer «oneliners» to clarity and performance, a bonus 1-liner version with suitably mangled names:-).

from itertools import groupby as g
def most_common_oneliner(L):
  return max(g(sorted(L)), key=lambda(x, v):(len(list(v)),-L.index(x)))[0]

Поиск часто встречающихся элементов в массиве

Задача: в массиве длиной N найти элемент, который повторяется больше N/2 раз.

Казалось бы, чего тут думать? Возьмём Dictionary<значение элемента, число появлений>, за один проход по массиву сосчитаем появления каждого элемента, потом выберем из словаря искомый элемент. Решение за O(N), куда может быть ещё быстрее?

Есть один нюанс: для словаря нам потребуется O(N) дополнительной памяти — в несколько раз больше размера исходного массива, и это при реализации словаря хоть хэш-таблицей, хоть деревом. Что будем делать, если наша цель — обработка сигнала неким устройством с маленькой памятью? Массив — замеры уровня сигнала, из которых один — «настоящий» передаваемый уровень, а остальные — шум и помехи. Неужели придётся для определения «настоящего» уровня возиться с хэш-таблицами и деревьями?

К счастью, нет: достаточно O(1) дополнительной памяти, и по-прежнему одного прохода по массиву. Алгоритм Бойера-Мура — тех самых Бойера и Мура, что придумали намного более известный алгоритм поиска подстроки — проще всего представить следующим образом: на вечеринке собрались N людей, и на каждом по одному элементу из массива. Когда встречаются двое, у которых элементы разные, они присаживаются это обсудить. В конце концов останутся стоять только люди с одинаковыми элементами; очевидно, это тот самый элемент, который встречался больше N/2 раз.

Реализация алгоритма Бойера-Мура занимает всего несколько строк:

int* majority(int[] array, int N) {
  int confidence = 0; // количество людей, не нашедших пары и оставшихся стоять
  int* candidate = NULL; // последний человек, не нашедший пару -- 
                         // возможно, его элемент встречается чаще всего

  // проходим по массиву и усаживаем пары с разными элементами
  for (int i = 0; i<N; i++) {

    // если до сих пор все сидят, то следующему пока придётся постоять
    if (confidence == 0) {
      candidate = array+i;
      confidence++;
    }

    // иначе следующий либо садится с одним из стоящих,
    // либо будет стоять вместе с ними, если у него такой же элемент
    else if (*candidate == array[i])) 
      confidence++;
    else 
      confidence--;
  }

  return confidence > 0 ? candidate : NULL;
}

В конце мы получаем «наиболее вероятного кандидата» на присутствие в N/2 экземплярах: если такой элемент в массиве действительно существует, то он будет найден; если же такого элемента нет, то возможно, стоять останется просто какой-то бедолага, которому не хватило пары. Для более строгой реализации majority требуется пройти по массиву второй раз и проверить, действительно ли найденный элемент встречается требуемое количество раз.

Усложним задачу. Теперь в массиве длиной N надо найти элементы, которые повторяются больше N/3 раз — если есть два, то оба, если есть один, то один.

Например, нашему устройству с маленькой памятью нужно принять двоичный сигнал с неизвестными уровнями нуля и единицы, но известно, что примерно половину времени передаётся ноль, примерно половину времени — единица, а любые отличные от них уровни сигнала — это помехи и дребезг от переключения.

Идею прошлого алгоритма несложно обобщить и для троек: пусть люди с разными элементами рассаживаются по трое. Значит, в конце вечеринки останутся стоять люди максимум с двумя разными элементами. Если какой-то элемент встречался больше N/3 раз, значит человек с ним гарантированно останется стоять, ведь сидящих троек получится не больше N/3. Как и в прошлом случае, если искомые элементы существуют — то они будут найдены, но если их нет — то найтись может кто попало.

Код мало отличается от предыдущего: по-прежнему один проход по массиву и O(1) дополнительной памяти.

void majority(int[] array, int N, int** cand1, int** cand2) {
  int conf1 = 0, conf2 = 0; // количество стоящих людей с двумя элементами
  *cand1 = NULL; *cand2 = NULL; // два стоящих человека с разными элементами

  // проходим по массиву и усаживаем тройки с разными элементами
  for (int i = 0; i<N; i++) {

    // у следующего такой же элемент, как у стоящих? тогда встанет вместе с ними
    if (conf1 > 0 && **cand1 == array[i])
      conf1++;
    else if (conf2 > 0 && **cand2 == array[i])
      conf2++;
    else // может, стоят только с одним элементом, или вообще стоящих нет?
      if (conf1 == 0) {
        *cand1 = array+i;
        conf1++;
      } else if (conf2 == 0) {
        *cand2 = array+i;
        conf2++;
      }
    else { // стоят с двумя другими элементами, так что усаживаем всю тройку
      conf1--;
      conf2--;
    }
  }

  if(conf1 == 0) *cand1 = NULL;
  if(conf2 == 0) *cand2 = NULL;
}

Этот алгоритм опубликован в 1982 американскими учёными Джаядевом Мисрой и Дэвидом Грисом (Jayadev Misra & David Gries), и в их работе используется более скучная метафора — мешок с N числами, из которого они извлекают по 3 разных числа за каждую операцию. Кроме того, их псевдокод не похож ни на один понятный современному программисту язык. Мне больше понравилось объяснение их алгоритма в позапрошлогоднем конспекте лекций американского профессора Амита Чакрабарти.

В наиболее общей форме, когда в массиве длиной N надо найти элементы, которые повторяются больше N/k раз — придётся-таки воспользоваться словарём. Хранить в словаре мы будем только те элементы, с которыми люди стоят — т.е. не больше k-1 записей.

int[] majority(int[] array, int N, int k) {
  // словарь стоящих людей изначально пуст
  Dictionary<int,uint> candidates = new Dictionary<int,uint>{};

  // проходим по массиву и усаживаем группы по k
  for (int i = 0; i<N; i++) {

    // у следующего такой же элемент, как у стоящих? тогда встанет вместе с ними
    if (candidates.ContainsKey(array[i]))
      candidates[array[i]]++;
    else // может, стоят менее чем с k-1 элементами?
      if (candidates.Count < k - 1)
        candidates[array[i]] = 1;
    else // стоят с k-1 другими элементами, так что усаживаем всю группу
      foreach(int l in candidates.Keys)
        if (candidates[l]-- == 0)              // (**)
          candidates.Remove(l);                // (*)
  }

  return candidates.Keys.ToArray();
}

В этой наиболее общей форме алгоритма — по-прежнему один проход по массиву и O(k) дополнительной памяти. Если мы пользуемся для реализации словаря хэш-таблицей, а все записи в словаре свяжем в список — тогда общая сложность алгоритма останется линейной: строчка (*) с удалением записи из словаря выполняется самое большее N раз, ведь на каждой итерации основного цикла в словарь добавляется не больше одной записи. Читателям в качестве упражнения предлагается понять, почему строчка (**) не нарушает линейности алгоритма.

Таким образом наше устройство с маленькой памятью смогло бы общаться с одним пушистым зверьком, недавно препарированным хабраумельцами. Сигналы этого зверька имеют пять логических уровней: полагаем k=6, и получаем все пять уровней прямо на ходу, даже без сохранения сигнала в память. Нужно только обеспечить протоколом, чтобы все пять уровней встречались в сигнале одинаково часто.

Для алгоритма Мисры-Гриса упоминаются и другие применения. Например, можно следить в реальном времени за трафиком в сети, и если некий один хост потребляет непропорционально большую часть трафика — начинать расследование. Так же можно следить за кликами по баннерам, за финансовыми транзакциями, за потоком инструкций в моделируемом процессоре… В общем, всюду, где большое число повторений — подозрительная аномалия.

За оживление текста иллюстрациями надо благодарить Nitatunarabe

Поиск и подсчет самых частых значений

Необходимость поиска наибольших и наименьших значений в любом бизнесе очевидна: самые прибыльные товары или ценные клиенты, самые крупные поставки или партии и т.д.

Но наравне с этим, иногда приходится искать в данных не топовые, а самые часто встречающиеся значения, что хоть и звучит похоже, но, по факту, совсем не то же самое. Применительно к магазину, например, это может быть поиск не самых прибыльных, а самых часто покупаемых товаров или самое часто встречающееся количество позиций в заказе, минут в разговоре и т.п.

В такой ситуации задачу придется решать немного по-разному, в зависимости от того, с чем мы имеем дело — с числами или с текстом.

Поиск самых часто встречающихся чисел

Предположим, перед нами стоит задача проанализировать имеющиеся данные по продажам в магазине, с целью определить наиболее часто встречающееся количество купленных товаров. Для определения самого часто встречающегося числа в диапазоне можно использовать функцию МОДА (MODE):

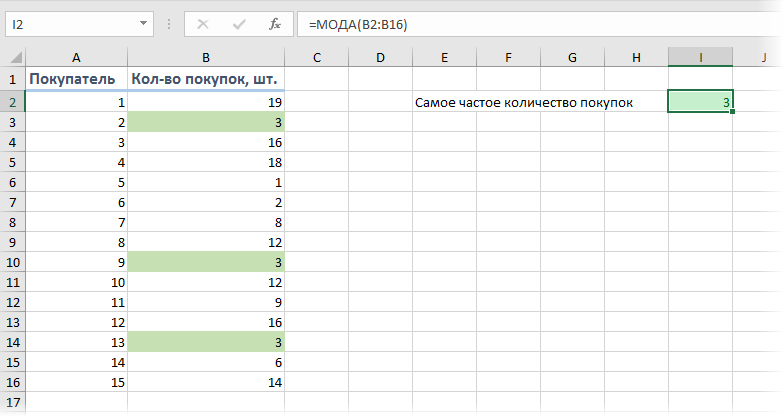
Т.е., согласно нашей статистике, чаще всего покупатели приобретают 3 шт. товара.

Если существует не одно, а сразу несколько значений, встречающихся одинаково максимальное количество раз (несколько мод), то для их выявления можно использовать функцию МОДА.НСК (MODE.MULT). Ее нужно вводить как формулу массива, т.е. выделить сразу несколько пустых ячеек, чтобы хватило на все моды с запасом и ввести в строку формул =МОДА.НСК(B2:B16) и нажать сочетание клавиш Ctrl+Shift+Enter.

На выходе мы получим список всех мод из наших данных:

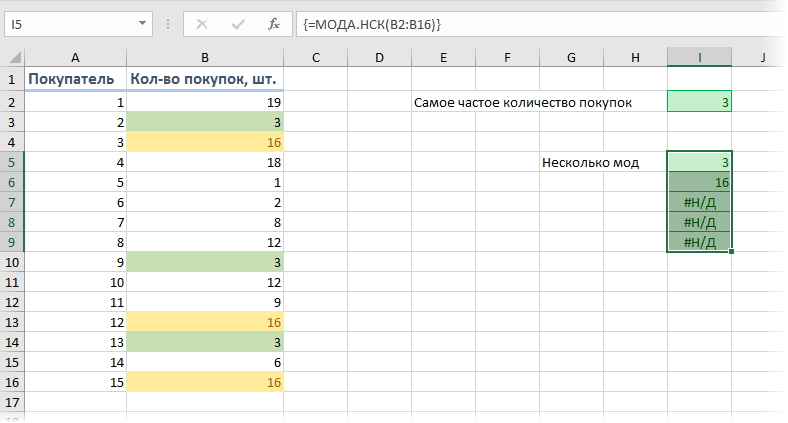
Т.е., судя по нашим данным, часто берут не только по 3, но и по 16 шт. товаров. Обратите внимание, что в наших данных только две моды (3 и 16), поэтому остальные ячейки, выделенные «про запас», будут с ошибкой #Н/Д.

Частотный анализ по диапазонам функцией ЧАСТОТА

Если же нужно проанализировать не целые, а дробные числа, то правильнее будет оценивать не количество одинаковых значений, а попадание их в заданные диапазоны. Например, нам необходимо понять какой вес чаще всего бывает у покупаемых товаров, чтобы правильно выбрать для магазина тележки и упаковочные пакеты подходящего размера. Другими словами, нам нужно определить сколько чисел попадает в интервал 1..5 кг, сколько в интервал 5..10 кг и т.д.

Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY). Для нее нужно заранее подготовить ячейки с интересующими нас интервалами (карманами) и затем выделить пустой диапазон ячеек (G2:G5) по размеру на одну ячейку больший, чем диапазон карманов (F2:F4) и ввести ее как формулу массива, нажав в конце сочетание Ctrl+Shift+Enter:

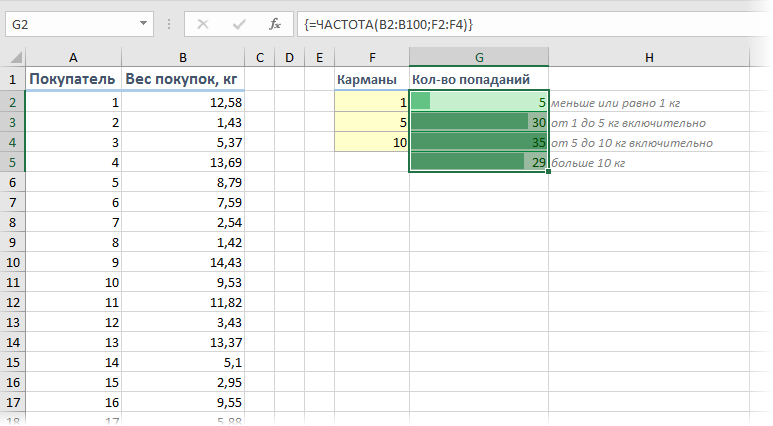
Частотный анализ сводной таблицей с группировкой

Альтернативный вариант решения задачи: создать сводную таблицу, где поместить вес покупок в область строк, а количество покупателей в область значений, а потом применить группировку — щелкнуть правой кнопкой мыши по значениям весов и выбрать команду Группировать (Group). В появившемся окне можно задать пределы и шаг группировки:

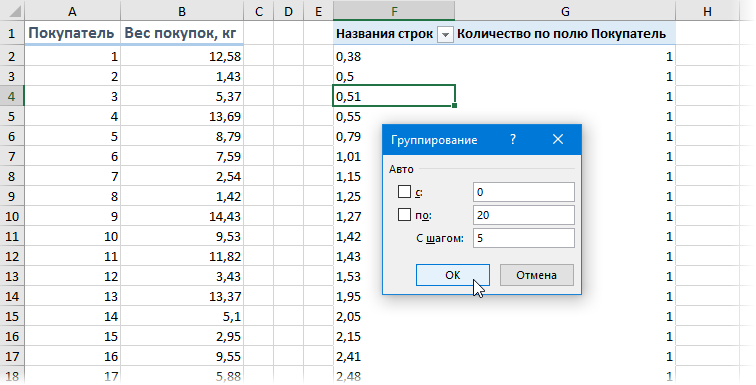
… и после нажатия на кнопку ОК получить таблицу с подсчетом количества попаданий покупателей в каждый диапазон группировки:

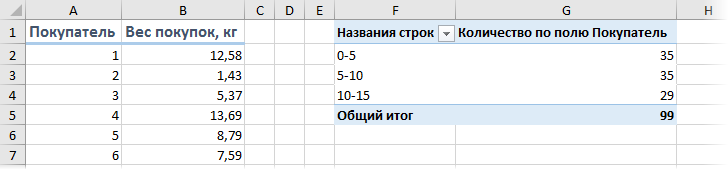
Минусы такого способа:

• шаг группировки может быть только постоянным, в отличие от функции ЧАСТОТА, где карманы можно задать абсолютно любые
• сводную таблицу нужно обновлять при изменении исходных данных (щелчком правой кнопки мыши — Обновить), а функция пересчитывается автоматически «на лету»

Поиск самого часто встречающегося текста

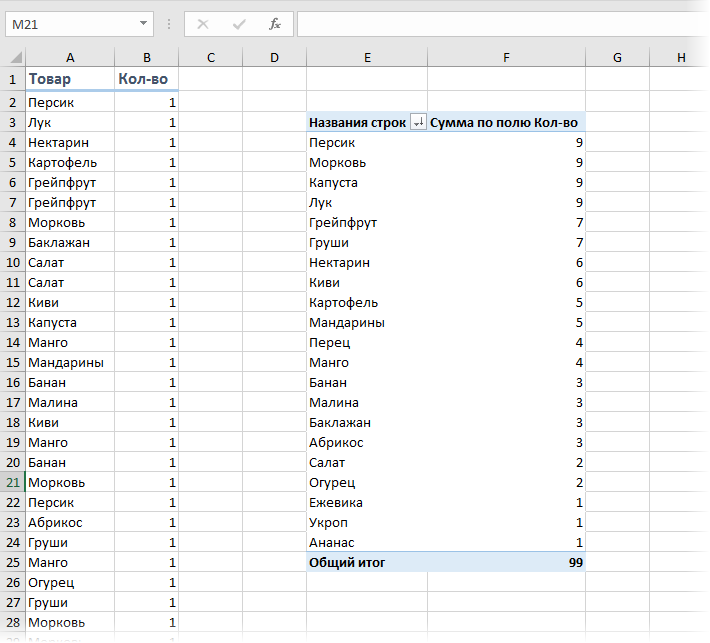
Если мы имеем дело не с числами, а с текстом, то подход к решению будет принципиально другой. Предположим, что у нас есть таблица из 100 строк с данными о проданных в магазине товарах, и нам нужно определить, какие товары покупались наиболее часто?

Самым простым и очевидным решением будет добавить рядом столбец с функцией СЧЁТЕСЛИ (COUNTIF), чтобы подсчитать количество вхождений каждого товара в столбце А:

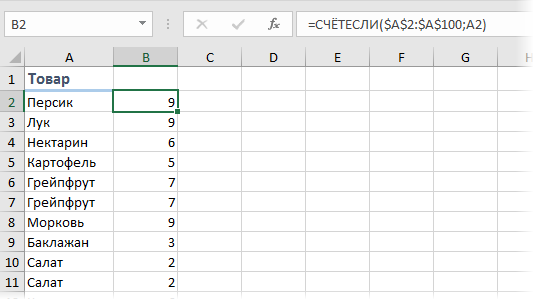
Затем, само-собой, отсортировать получившийся столбец по убыванию и посмотреть на первые строчки.

Или же добавить к исходному списку столбец с единичками и построить по получившейся таблице сводную, подсчитав суммарное количество единичек для каждого товара:

Если исходных данных не очень много и принципиально не хочется пользоваться сводными таблицами, то можно использовать формулу массива:

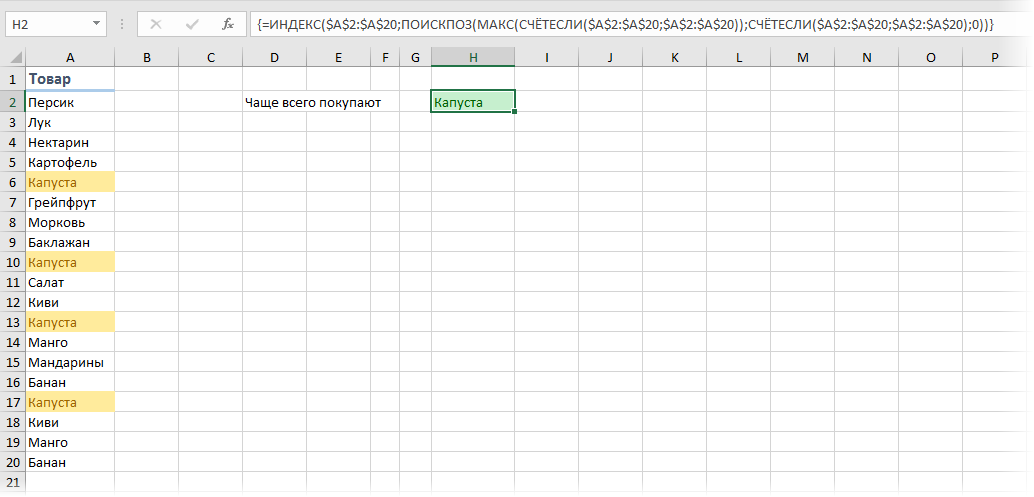
Давайте разберем ее по кусочкам:

• СЧЁТЕСЛИ(A2:A20;A2:A20) – формула массива, которая ищет по очереди количество вхождений каждого товара в диапазоне A2:A100 и выдаст на выходе массив с количеством повторений, т.е., фактически, заменяет собой дополнительный столбец
• МАКС – находит в массиве вхождений самое большое число, т.е. товар, который покупали чаще всего
• ПОИСКПОЗ – вычисляет порядковый номер строки в таблице, где МАКС нашла самое большое число
• ИНДЕКС – выдает из таблицы содержимое ячейки с номером, который нашла ПОИСКПОЗ

Ссылки по теме

• Подсчет количества уникальных значений в списке
• Извлечение уникальных элементов из списка с повторами
• Группировка в сводных таблицах