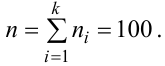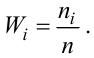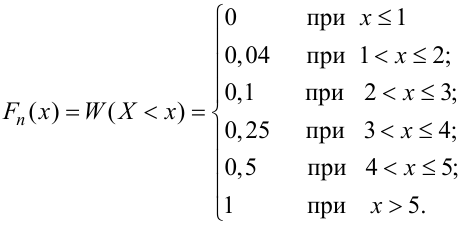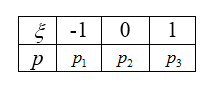Начальные и центральные моменты случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Начальные моменты
Начальным моментом порядка
случайной величины
называют математическое ожидание величины
:
В
частности:
Пользуясь
этими моментами, формулу для вычисления дисперсии
можно записать так:
Центральные моменты
Кроме
моментов случайной величины
целесообразно рассматривать моменты отклонения
.
Центральным моментом порядка
случайной величины
называют математическое ожидание величины
:
В
частности,
Взаимосвязь центральных и начальных моментов
Легко
выводятся соотношения, связывающие начальные и центральные моменты:
Моменты
более высоких порядков применяются редко.
Формулы для вычисления моментов дискретных и непрерывных случайных величин
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Нетрудно
заметить, что при
первый
начальный момент случайной величины
есть ее
математическое ожидание, то есть
, при
второй
центральный момент – дисперсия, то есть
.
Асимметрия и эксцесс случайной величины
Третий центральный момент
служит для
характеристики асимметрии (скошенности) распределения. Он имеет размерность
куба случайной величины. Чтобы получить безразмерную величину, ее делят на
, где
– среднее
квадратическое отклонение случайной величины
. Полученная величина
называется
коэффициентом асимметрии случайной величины:
Если распределение симметрично относительно
математического ожидания, то коэффициент асимметрии
.
Четвертый центральный момент
служит для
характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом (или коэффициентом
эксцесса) случайной величины называется число
Число 3 вычитается из отношения
потому, что для
наиболее часто встречающегося нормального распределения отношение
. Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.
Смежные темы решебника:
- Асимметрия и эксцесс распределения
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Дискретная
случайная величина X задана законом распределения:
|
|
1 | 3 | 4 | 5 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти начальные моменты первого, второго и третьего
порядков.
Решение
Найдем
начальный момент 1-го порядка:
Начальный
момент 2-го порядка:
Начальный
момент 3-го порядка:
Ответ:
.
Пример 2
Дискретная
случайная величина X задана законом распределения:
|
|
0 | 3 | 5 | 6 |
|
|
0,3 | 0,2 | 0,3 | 0,2 |
Найти центральные моменты первого, второго,
третьего и четвертого порядков.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Центральный
момент первого порядка равен нулю:
Для
вычисления центральных моментов удобно воспользоваться формулами, выражающими
центральные моменты через начальные, поэтому предварительно найдем начальные
моменты:
Начальный
момент 2-го порядка:
Начальный
момент 3-го порядка:
Начальный
момент 4-го порядка:
Найдем центральные моменты:
Ответ:
.
Пример 3
Непрерывная случайная
величина X задана плотностью распределения:
Найти
математическое ожидание, дисперсию, асимметрию и эксцесс.
Решение
Математическое
ожидание (начальный момент первого порядка):
Начальный
момент второго порядка:
Дисперсия
(центральный момент второго порядка):
Среднее
квадратическое отклонение:
Начальный
момент третьего порядка:
Начальный
момент четвертого порядка:
Вычисляем
центральные моменты третьего и четвертого порядков:
Коэффициент
асимметрии:
Эксцесс:
Ответ:
.
- Краткая теория
- Примеры решения задач
Моменты случайных величин.
Для
характеристики различных свойств
случайных величин используются начальные
и центральные моменты.
Начальным
моментом k-го
порядка случайной
величины Х называется математическое
ожидание k-й
степени этой величины:
αК
= М [XК].
Для
дискретной случайной величины
αК
=
Для непрерывной
случайной величины
Ц
0
Х = Х – М[Х]
ентрированной случайной величиной
называется отклонение случайной величины
от ее математического ожидания:
Условимся отличать
центрированную с.в. значком 0
наверху.
Центральным
моментом S-го
порядка
называется математическое ожидание
S-й
степени центрированной случайной
величины
S
= M [(X – mx)S].
Для дискретной
случайной величины
S
=
(xi
– mx)S
pi.
Для непрерывной
случайной величины
.
Свойства моментов случайных величин
-
начальный момент
первого порядка равен математическому
ожиданию (по определению):
α1
= М [X1]
= mx.
-
центральный
момент первого порядка всегда равен
нулю (докажем на примере дискретной с.
в.):
1
= M
[(X – mx)1]
=(xi
– mx)
pi
=xi
pi
–mx
pi
= mx–mxpi
=mx–mx=
0.
-
центральный момент
второго порядка характеризует разброс
случайной величины вокруг ее
математического ожидания.
Центральный момент
второго порядка называется дисперсией
с. в. и обозначается D[X]
или Dx
Дисперсия имеет
размерность квадрата случайной величины.
-
Среднее
квадратическое отклонение
σх
= √Dx.
σх
– также
как и Dx
характеризует
разброс случайной величины вокруг ее
математического ожидания но имеет
размерность случайной величины.
-
второй начальный
момент α2
характеризует степень разброса случайной
величины вокруг ее математического
ожидания, а также смещение случайной
величины на числовой оси
Связь первого и
второго начальных моментов с дисперсией
(на примере непрерывной с. в.):
-
третий центральный
момент характеризует степень разброса
случайной величины вокруг математического
ожидания, а также степень асимметрии
распределения случайной величины.
f(xср)
> f(-xср)
Для симметричных
законов распределения m3
= 0.
Для характеристики
только степени асимметрии используется
так называемый коэффициент асимметрии
Sk = m3
/σ3
Для симметричного
закона распределения Sk
= 0
-
четвертый
центральный момент характеризует
степень разброса случайной величины
вокруг математического ожидания, а
также степень островершинности закона
распределения.
Для характеристики
только степени островершинности
распределения используется эксцесс
(обозначается
εх):
εх
= m4
/σ4
– 3
εх2
= 0;(нормальный закон распределения) εх1
0; εх3
0.
Задача.
Случайна величина Х задана плотностью
распределения вероятности
f(x) =
Найти: F(x),
mx,
α2,
Dx,
σx
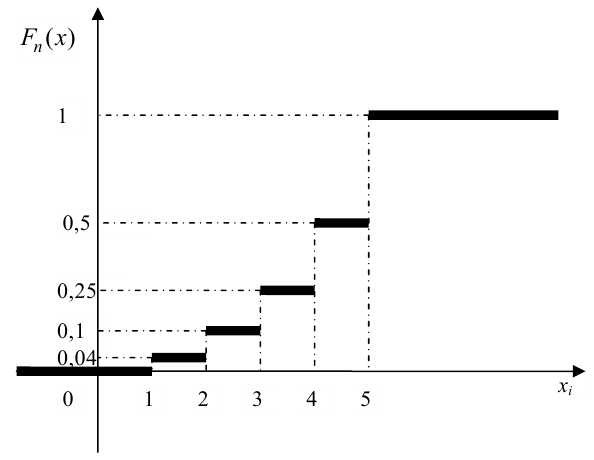
и построить
графики функций f(x)
и F(x).
Математическое
ожидание:
Второй начальный
момент:
Дисперсия: Dx
= α2
–
mx2
= 1/2 – 4/9 =
1/18
Средне квадратичное
отклонение: σх
= √Dx
= √(1/18) = √2/6.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обобщенными числовыми характеристиками для случайных величин в теории вероятностей а также математической статистике являются начальные и центральные моменты. Задачи на отыскание моментов являются неотъемлемой частью теории вероятностей и математической статистики. Начальным моментом k-го порядка случайной величины Х называют математическое ожидание от величины в k-ой степени
Когда
Когда 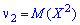
Для дискретной случайной величины 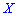
для непрерывной интегрированием
Если непрерывная величина задана интервалом 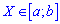
Центральным моментом k-го порядка называют математическое ожидание от величины
Когда
для 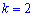
при 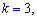
при 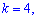
и так далее.
Для дискретной случайной величины центральные моменты вычисляют по формуле
для непрерывной по следующей
Если случайная величина определена интервалом 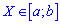
Рассмотрим пример отыскания приведенных величин.
————————————
Пример 1. Задана функция плотности вероятностей
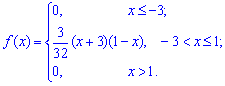
Вычислить начальные и центральные моменты второго и третьего порядка 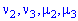
Решение. Для вычисления начальных моментов выполним интегрирование по вышеприведенным формулам
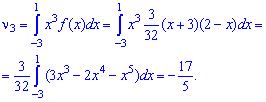
Промежуточные операции при интегрировании пропущены, они занимают много места, а Вам главное иметь инструкцию для вычислений, так как примеры у Вас будут другие.
Для вычисления центральных моментов инерции необходимо знать математическое ожидание случайной величины, поэтому определяем его первее
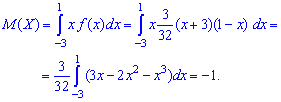
Найдено математическое ожидание подставляем в формулу центральных моментов. В случае 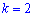
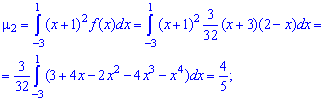
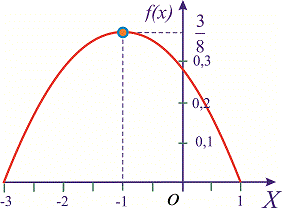
и при 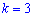
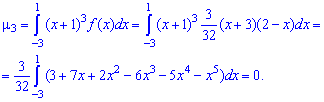
На этом решения примера завершено, функция плотности вероятностей приведена на графике
————————————
Примеры нахождения начальных и центральных моментов будут рассмотрены в следующей статье. Задачи совсем не сложные, а вычисления величин сводится к возведения в степень, интегрирование, умножение и суммирование.
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 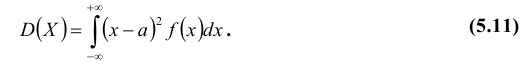
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 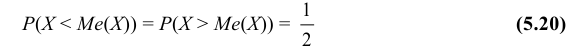
Пример №2
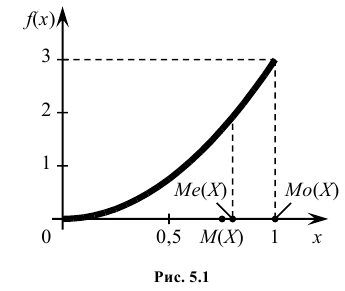
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 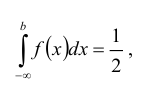
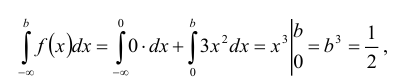
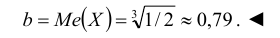
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 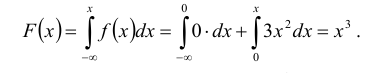
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
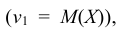
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 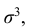
Полученная величина А называется коэффициентом асимметрии случайной величины: 
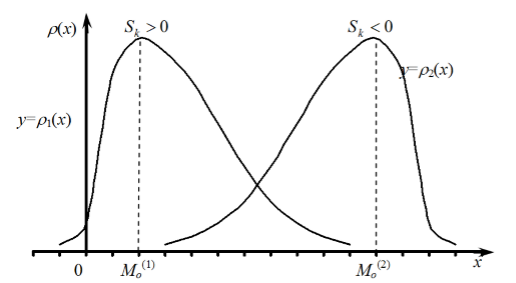
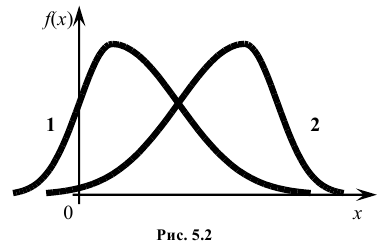
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
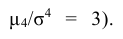
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 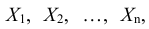
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 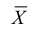
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
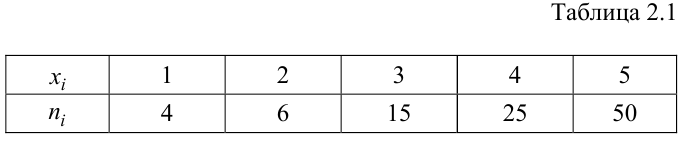
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
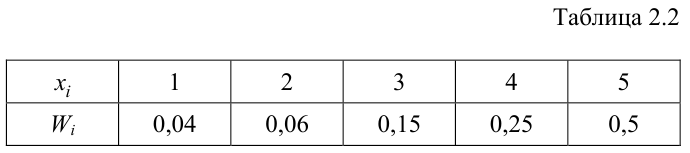
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 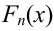
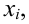
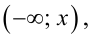
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
[{rm M} left({rm X}right)=sum limits _{i=1}^{n}x_{i} p_{i} {rm .} ]
Определение 2
Дисперсией (рассеиванием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
[Dleft(Xright)=Mleft(left(X-Mleft(Xright)right)^{2} right).]
Обобщением рассмотренных нами числовых характеристик случайной величины являются начальные и центральные моменты $k$-го порядка.
Начальным моментом $k$-го порядка случайной величины $X$ называется математическое ожидание случайной величины $X^{k} $:
Для дискретной случайной величины имеем:
или
если множество значений случайной величины бесконечно, и ряд в правой части сходится абсолютно.
Для непрерывной случайной величины $X$
если несобственный интеграл в правой части сходится; $f(x)$ — плотность распределения вероятностей $X$.
Математическое ожидание есть начальный момент первого порядка:
Центральным моментом $k$-го порядка случайной величины $X$ называется математическое ожидание $k$-ой степени соответствующей центрированной случайной величины $mathop{X^{k} }limits^{} , $:
Для дискретной случайной величины имеем:
или
если множество значений случайной величины бесконечно, и ряд в правой части сходится абсолютно.
Для непрерывной случайной величины $X$
если несобственный интеграл в правой части сходится; $f(x)$ — плотность распределения вероятностей $X$.
Отметим, что $mu _{1} (X)=0$ для любой случайной величины $X$, а центральный момент второго порядка представляет собой дисперсию:
«Начальные и центральные моменты» 👇
Если плотность распределения случайной величины $X$ симметрична относительно математического ожидания, то все её центральные моменты нечетных порядков обращаются в нуль. На этом свойстве основывается использование $mu _{3} (X)$ в качестве характеристики ассиметрии распределения. Для того, чтобы избавиться от кубической размерности, поделим его на $sigma ^{3} (X)$:
Это так называемый коэффициент ассиметрии или скошенности.
Если кривая плотности распределения непрерывной случайной величины такова, что справа от моды расположена ее «длинная часть», а слева — «короткая», то коэффициент асимметрии $S_{k} $ положителен.
Коэффициент асимметрии $S_{k} $ отрицателен, если «длинная часть» кривой распределения расположена слева от моды (рис. 1).
Рисунок 1.
Отношение центрального момента четвертого порядка $mu _{4} (X)$ к $sigma ^{4} (X)$ называется эксцессом и служит характеристикой «плосковершинности» графика плотности распределения случайной величины $X$:
Моменты более высоких порядков используются редко.
Использование на практике
Пример 1
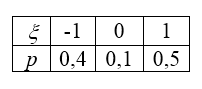
Дан возможные значения дискретной случайной величины $xi$: $x_{1} =-1, $, $x_{2} =0, $, $x_{3} =1, $, а также известно математическое ожидание этой величины и ее квадрат: $Mxi =0,1, $; $M(xi ^{2} )=0,9, $. Найти вероятность $p_{1} , $, $p_{2} ,$ $p_{3} ,$ соответствующие возможным значениям $x_{1} $, $x_{2} $, $x_{3} $.
Решение.
Запишем таблицу расспределения нешей (рис. 2) случайной величины $xi$:
Рисунок 2.
[p_{1} +p_{2} +p_{3} =1, ]
Используя определение математического ожидания дискретной случайной величины и начальный момент второго порядка, получим два уравнения:
[left{begin{array}{l} {-p_{1} +p_{3} =0,1;} \ {p_{1} +p_{3} =0,9.} end{array}right. , ]
Когда решить систему двух уравнений с двумя неизвестными, получим $p_{1} =0,4$, $p_{3} =0,5$. Так как сумма вероятностей, которые входят в ряд распределения равна 1, то найдем $p_{2} $:
[p_{2} =1-p_{1} -p_{3} =1-0,4-0,5=0,1, .]
Найденые значения запишем в таблицу расспределения случайной величины $xi$:
Рисунок 3.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме














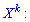
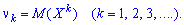
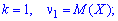
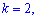
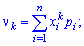
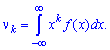
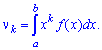
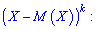
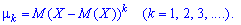
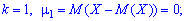
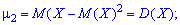
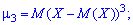
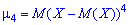
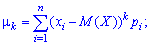
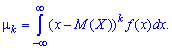
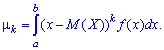
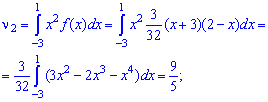
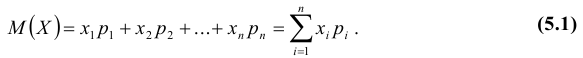
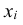
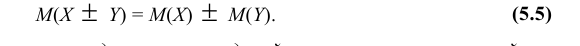


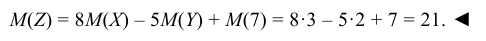







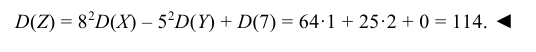
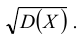

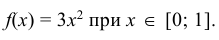

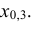
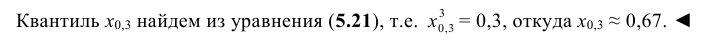



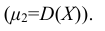
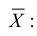
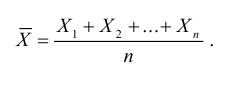

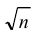 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: