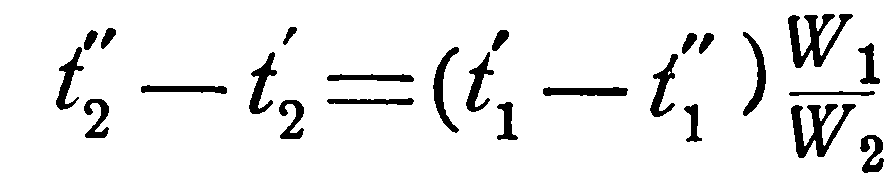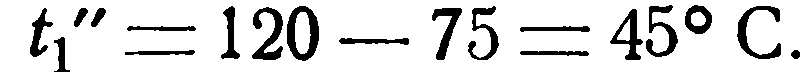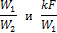Which takes more energy to heat up: air or water? How about water versus metal or water versus another liquid like soda?
These questions and many others are related to a property of matter called specific heat. Specific heat is the amount of heat per unit of mass needed to raise a substance’s temperature by one degree Celsius.
So it takes more energy to heat up water than air because water and air have different specific heats.
TL;DR (Too Long; Didn’t Read)
Use the formula:
Q = mcΔT, also written Q = mc(T — t0)
to find the initial temperature (t0) in a specific heat problem.
In fact, water has one of the highest specific heats of any «common» substance: It’s 4.186 joule/gram °C. That’s why water is so useful in moderating the temperature of machinery, human bodies and even the planet.
Equation for Specific Heat
You can use the property of specific heat to find a substance’s initial temperature. The equation for specific heat is usually written:
Q = mcΔT
where Q is the amount of heat energy added, m is the substance’s mass, c is specific heat, a constant, and ΔT means «change in temperature.»
Make sure your units of measurement match the units used in the specific heat constant! For example, sometimes the specific heat may use Celsius. Other times, you’ll get the SI unit for temperature, which is Kelvin. In these cases, the units for specific heat will either be Joules/gram °C or else Joules/gram K. The same could happen with grams versus kilograms for the mass, or Joules to Bmu for energy. Be sure to check the units and make any conversions needed before you get started.
Using Specific Heat to Find Initial Temperature
ΔT can also be written (T — t0), or a substance’s new temperature minus its initial temperature. So another way to write the equation for specific heat is:
Q = mc(T — t0)
So this rewritten form of the equation makes it simple to find initial temperature. You can plug in all the other values that you’re given, then solve for t0.
For example: Say you add 75.0 Joules of energy to 2.0 grams of water, raising its temperature to 87 °C. Water’s specific heat is 4.184 Joules/gram °C. What was the initial temperature of the water?
Plug the given values into your equation:
75.o J = 2.0 g x (4.184 J/g°C) x (87 °C — t0).
Simplify:
75.o J = 8.368 J/°C x (87 °C — t0).
8.96 °C = (87 °C — t0)
78°C = t0.
Specific Heat and Phase Changes
There’s one important exception to keep in mind. The specific heat equation doesn’t work during a phase change, for example, from a liquid to a gas or a solid to a liquid. That’s because all the extra energy that’s being pumped in is being used for the phase change, not for increasing the temperature. So the temperature stays flat during that period, throwing off the relationship between energy, temperature and specific heat in that situation.
Начальная температура тела 60 С равна температуре окружающей среды.
Начальная температура тела равна t0; в момент т0 температура поверхности тела принимает значение fn которое остается затем неизменным. Требуется найти температурное поле тела и количество переданной теплоты.
Начальная температура тела 60 С равна температуре окружающей среды.
Начальная температура тела 6о С равна температуре окружающей среды.
Начальная температура тела вв С равна температуре окружающей среды.
Если начальная температура тела равномерна и равна Та, то полное значение температуры Т равно ДГ 7Н, где АГ — приращение температуры.
Пусть начальная температура тела равна / нач, а конечная температура — / кон.
Фнач — начальная температура тела, С.
При этом полагаем, что начальная температура тела равна нулю, а граничная поверхность поддерживается при нулевой температуре.
Тер — температура среды; Т0 — начальная температура тела; Bi — — критерий Био; Fo — — критерий Фурье; г / г, — относительный радиус.
Величина Т является температурой в какой-либо точке, отсчитываемой от известной равномерной начальной температуры тела.
Во всех рассмотренных нами задачах температура окружающей среды изменялась непрерывно от начальной температуры тела. Исключением был последний пример, в котором в начальный момент на поверхности тела происходит скачок температуры. Отметим, что при непрерывном изменении температуры поверхности тела удовлетворительные результаты расчета получаются уже по температурному полю в первом приближении.
Скорость охлаждения изменяется примерно на 7 град / сек при изменении начальной температуры тела на 50 С.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Как найти начальную температуру тела?
Приведите пример.
На странице вопроса Как найти начальную температуру тела? из категории Физика вы найдете
ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.
Как вы думаете, что быстрее нагревается на плите: литр воды в кастрюльке или же сама кастрюлька массой 1 килограмм? Масса тел одинакова, можно предположить, что нагревание будет происходить с одинаковой скоростью.
А не тут-то было! Можете проделать эксперимент – поставьте пустую кастрюльку на огонь на несколько секунд, только не спалите, и запомните, до какой температуры она нагрелась. А потом налейте в кастрюлю воды ровно такого же веса, как и вес кастрюли. По идее, вода должна нагреться до такой же температуры, что и пустая кастрюля за вдвое большее время, так как в данном случае нагреваются они обе – и вода, и кастрюля.
Однако, даже если вы выждете втрое большее время, то убедитесь, что вода нагрелась все равно меньше. Воде потребуется почти в десять раз большее время, чтобы нагреться до такой же температуры, что и кастрюля того же веса. Почему это происходит? Что мешает воде нагреваться? Почему мы должны тратить лишний газ на подогрев воды при приготовлении пищи? Потому что существует физическая величина, называемая удельной теплоемкостью вещества.
Эта величина показывает, какое количество теплоты надо передать телу массой один килограмм, чтобы его температура увеличилась на один градус Цельсия. Измеряется в Дж/(кг * ˚С). Существует эта величина не по собственной прихоти, а по причине разности свойств различных веществ.
Удельная теплоемкость воды примерно в десять раз выше удельной теплоемкости железа, поэтому кастрюля нагреется в десять раз быстрее воды в ней. Любопытно, что удельная теплоемкость льда в два раза меньше теплоемкости воды. Поэтому лед будет нагреваться в два раза быстрее воды. Растопить лед проще, чем нагреть воду. Как ни странно звучит, но это факт.
Обозначается удельная теплоемкость буквой c и применяется в формуле для расчета количества теплоты:
где Q – это количество теплоты,
c – удельная теплоемкость,
m – масса тела,
t2 и t1 – соответственно, конечная и начальная температуры тела.
По этой формуле можно рассчитать количество тепла, которое нам необходимо, чтобы нагреть конкретное тело до определенной температуры. Удельную теплоемкость различных веществ можно найти из соответствующих таблиц.
А что насчет удельной теплоемкости газов? Тут все запутанней. С твердыми веществами и жидкостями дело обстоит намного проще. Их удельная теплоемкость – величина постоянная, известная, легко рассчитываемая. А что касается удельной теплоемкости газов, то величина эта очень различна в разных ситуациях. Возьмем для примера воздух. Удельная теплоемкость воздуха зависит от состава, влажности, атмосферного давления.
При этом, при увеличении температуры, газ увеличивается в объеме, и нам надо ввести еще одно значение – постоянного или переменного объема, что тоже повлияет на теплоемкость. Поэтому при расчетах количества теплоты для воздуха и других газов пользуются специальными графиками величин удельной теплоемкости газов в зависимости от различных факторов и условий.
Предыдущая тема: Количество теплоты: формула, расчет
Следующая тема:   Энергия топлива: удельная теплота сгорания + ПРИМЕРЫ
Все неприличные комментарии будут удаляться.
все для проектирования
Формула расчета конечной температуры воды после смещения холодной и горячей:
где: Тс — температура смещенной воды, град.
М1 — масса холодной воды, кг
М2 — масса горячей воды, кг
Т1 — температура холодной воды, град.
Т2 — температура горячей воды, град.
Пример 1:
холодная вода 10 литров температурой 5 град смешивается с горячей водой 8 литров 60 градусов.
Необходимо определить конечную температуру воды. Подставляем все значения в формулу 1:
Формула расчета количество холодной и горячей воды в зависимости от температуры:
Бывает задача стоит в обратном направлении. Когда наоборот известно какую температуру необходимо иметь на выходе и общий вес воды, но не известна масса холодной и горячей воды. Тогда из формула 1 выводим новую формулу:
Пример 2:
из циркуляционного душа воды выходит температурой 36 градусов и объемом 40 литров. Необходимо определить количество холодной и горячей воды.
Как правило холодная вода имеет расчетную температуру 5 градусов. Горячая вода — 60 градусов.
Подставляем значения в формулу 2 и 3:
М1=(36*40-60*40)/(5-60)=17,45 литров холодной воды
М2=40-17,45=22,55 литров горячей воды
Удачного Вам дня! И успешных проектов!
Выше конечной целью теплового расчете являлось определение поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это — так называемый поверочный расчет.
При решении такой задачи известными являются следующие величины: поверхность нагрева F, коэффициент теплопередачи k, водяные эквиваленты W1 и W2 и начальные температуры t1’ и t2’, а искомыми: конечные температуры t1” и t2” и количество переданного тепла Q.
В приближенных расчетах можно исходить из следующих представлений. Количество тепла, отдаваемое горячей жидкостью, равно:
(2.13)
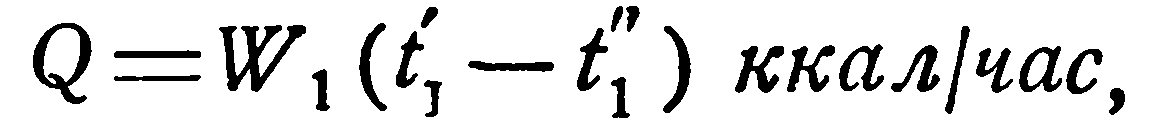
откуда конечная температура ее t1” определяется соотношением:
(a)
Соответственно для холодной жидкости имеем:
(2.14)
(b)
Если принять, что температуры рабочих жидкостей меняются по линейному закону, то
(с)
Вместо неизвестных t1” и t2” подставим их значения из уравнений (а) и (b), тогда получим:
(d)
Произведя дальнейшее преобразование, имеем:
(e)
откуда окончательно получаем:
(2.15)
Зная количество переданного тепла Q, очень просто формулам (а) и (b) определить и конечные температуры рабочих жидкостей t1” и t2”.
Приведенная схема расчета, хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока ниже приводится вывод более точных формул.
1. Прямоток. Выше было показано, что температурный напор изменяется по экспоненциальному закону:
(2.16)
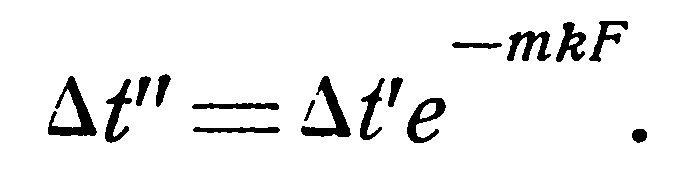
Имея в виду, что
и, что в конце поверхности нагрева Δt” = t1’ – t2’, то, подставляя эти значения в уравнение (19), последнее можно представить в следующем виде:
(2.17)
Однако, это уравнение дает лишь разности температур. Чтобы отсюда получить конечные температуры в отдельности, необходимо обе части равенства вычесть из единицы:
(2.18)
(2.19)
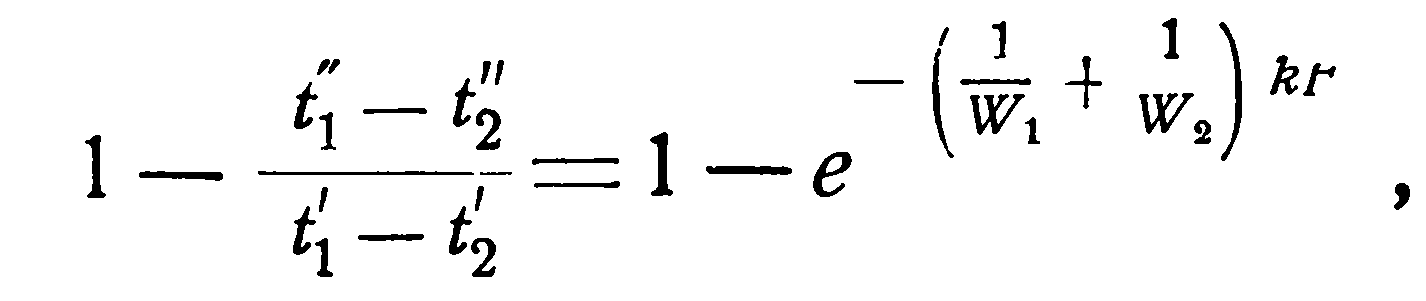
[см. разд.2.1 уравнение (2.5)].
то, подставляя это значение в левую часть уравнения (2.19), получаем:
(2.20)
Последнее уравнение, показывает, что изменение температуры горячей жидкости δt1 равно некоторой доле П располагаемого начального температурного напора, t1’ – t2’; эта доля зависит только от двух безразмерных параметров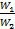 
и 
.
Аналогичным образом из уравнения (2.19) можно получить выражение и для изменения температуры холодной жидкости, а именно:
(2.21)
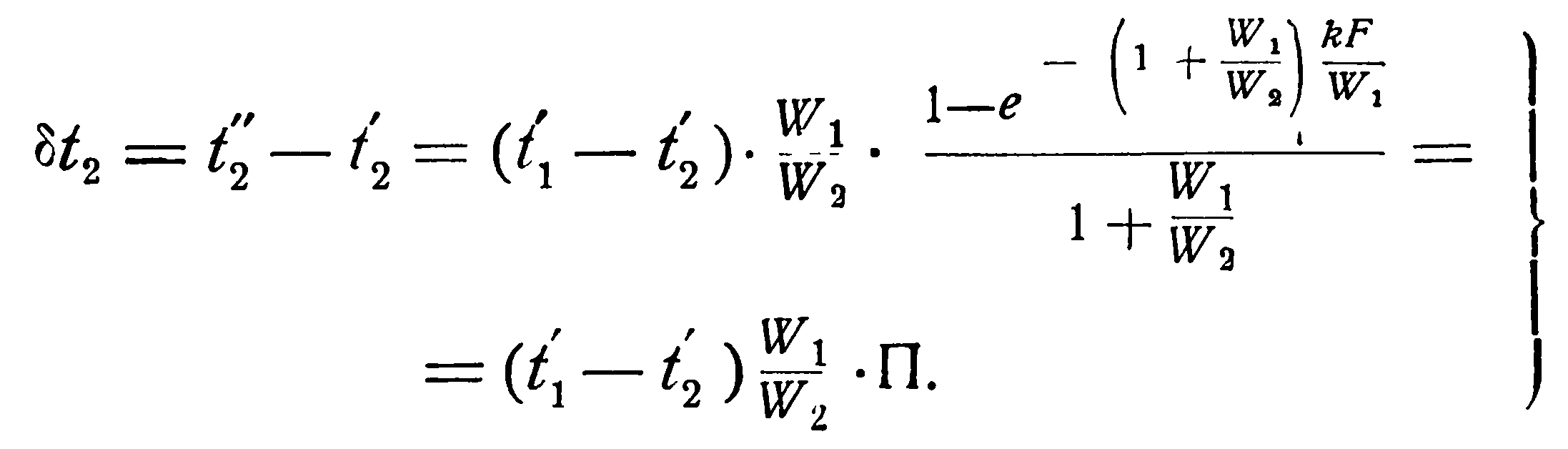
Определив изменения температур рабочих жидкостей и зная их начальные температуры, легко определить конечные:
(2.22)
Расход тепла определяется путем умножения водяного эквивалента жидкости на изменение ее температуры:
(2.23)
Значение функции 
приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение Fx.
Пример 2.2. Имеется водяной холодильник с поверхностью нагрева F=8 м 2 . Определить конечные температуры жидкостей и часовое количество передаваемого тепла Q, если заданы следующие величины: V1= 0,25 м 3 /час, γ1 = 1100 кг/м 3 , cp1 = 0,727 ккал/кг °С и t1’ = 120 °С Для охлаждения в распоряжении имеется 1000 л воды в час при температуре t2’ = 10 °С. Кроме того, известно значение коэффициента теплопередачи k = 30 ккал/м 2 час °С.
Соответствующее значение функции П находим из рис.2.5:
Рис. 2.5. 
— вспомогательная функция для расчета конечной температуры при прямотоке
Изменение (понижение) температуры горячей жидкости согласно уравнению (2.20) равно:
Следовательно, конечная температура ее равна:
Количество переданного тепла в час определится по уравнению (2.23)
Изменение температуры холодной жидкости определяется по уравнению (2.21). Но его можно также определить и из соотношения Q = W2 (t2” — t2’), откуда
2. Противоток. Для противотока расчетные формулы выводятся так же, как и для прямотока. Окончательно они имеют следующий вид:
(2.24)
(2.25)
(2.26)
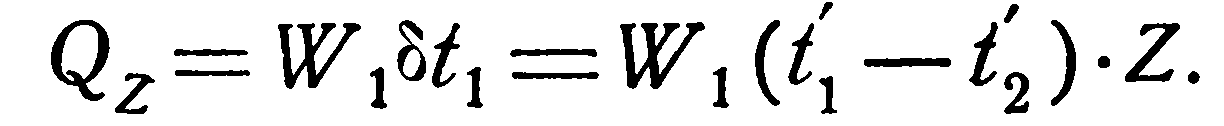
В частном случае, когда 
формулы
(2.24) – (2.26) принимают вид:
(2.27)
(2.28)
(2.29)
Значение функции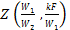 
приведено на рис. 2.6.
Рис. 2.6. 
— вспомогательная функция для расчета конечной температуры при противотоке
Для расчета промежуточных значений температуры рабочих жидкостей и количества переданного тепла в формулах (2.23) – (2.29) в числителе значение F заменяется на Fx, а в знаменателе остается значение полной поверхности F.
Пример 2.3. Если взять тот же теплообменник, который был рассмотрен в условиях прямотока, и допустить, что условия теплопередачи остаются без изменения (k = 30 ккал/м 2 час °С), то получим следующие соотношения:
Из рис. 2.6 находим значение функции Z:
Изменение температуры горячей жидкости равно [уравнение (2.24)]:
Конечная температура ее:
Изменение температуры холодной жидкости [уравнение (2.25)];
Конечная температура ее:
Количество переданного тепла в час [уравнение (2.26)]:
Таким образом, в случае противотока в теплообменнике происходит более глубокое охлаждение горячей жидкости.
3. Сравнение прямотока с противотоком. Чтобы выявить преимущество одной схемы перед другой, достаточно сравнить количество передаваемого тепла при прямотоке и противотоке при равенстве прочих условий. Для этого необходимо уравнение (2.23) разделить на уравнение (2.26). В результате этого действия мы получаем новую функцию тех же двух безразмерных аргументов
характер изменения которой графически показан на рис. 2.7.
Рис. 2.7. 
-сравнение прямотока с противотоком
Из рисунка следует, что схемы можно считать равноценными в том случае, если водяные эквиваленты обеих жидкостей значительно отличаются один от другого (при 
и при 
) или если значение параметра 
— мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку 
, то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.
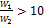
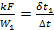
При конденсации и кипении температура жидкости постоянна. Это означает, что водяной эквивалент такой жидкости бесконечно велик. В этом случае прямоток и противоток равнозначны, и уравнения (2.23) и (2.26) становятся тождественными. Конечная температура той жидкости, для которой водяной эквивалент имеет конечное значение, определяется следующим образом.
При конденсации паров;
(2.30)
(2.31)
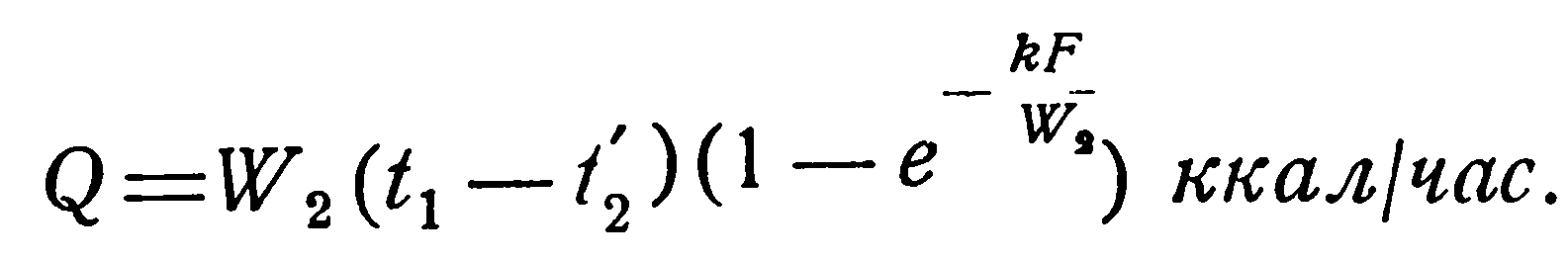
При кипении жидкостей:
(2.32)
(2.33)
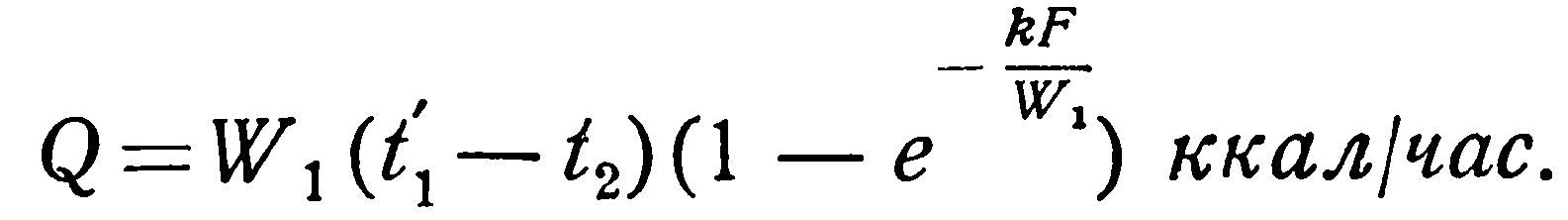
Вместо t1 и t2 в уравнения (2.30) – (2.33) можно подставить температуру стенки, значение которой при этом также постоянно. Значения функции 
находятся из таблиц показательных функций.
В случае перекрестного тока конечные температуры рабочих жидкостей находятся между конечными температурами для прямотока и противотока. Поэтому в приближенных расчетах можно пользоваться методом расчета одной из указанных схем. Если одна из жидкостей движется навстречу другой зигзагообразно (смешанный ток), то расчет может быть произведен, как для противотока.
4. Влияние тепловых потерь и проницаемости стенок.Все вышеприведенные формулы справедливы для случая, когда тепловые потери во внешнюю среду равны нулю. В действительности они всегда имеются. Более или менее точно учесть их влияние, вообще говоря, возможно, однако расчетные формулы при этом становятся громоздкими. Поэтому для учета влияния тепловых потерь в практике обычно применяется приближенный метод, который состоит в следующем.
Тепловые потери со стороны горячей жидкости вызывают более сильное падение ее .температуры. Это равносильно случаю, когда теплоотдающая жидкость в аппарате без потерь в окружающую среду имела бы меньшее значение водяного эквивалента. Поэтому влияние потерь в окружающую среду можно учесть, изменив водяной эквивалент теплоотдающей жидкости в тепловом аппарате таким образом, чтобы в последнем происходило такое же понижение температуры, как и при потоке с действительным водяным числом при наличии тепловых потерь. Внешние тепловые потери со стороны холодной жидкости оказывают обратное влияние, они уменьшают повышение температуры жидкости, что приводит к кажущемуся увеличению ее водяного эквивалента.
Наличие присоса наружного холодного воздуха оказывает такое же влияние, как и внешняя потеря тепла. Присосанный вездух на горячей стороне понижает температуру горячей жидкости (газа) точно так же, как если бы теплообменный аппарат был абсолютно непроницаем, но жидкость имела меньшее значение водяного эквивалента. Присос вездуха на холодной стороне понижает температуру холодной жидкости, что равносильно увеличению значения водяного эквивалента.
Если потеря тепла составляет р% к общему количеству передаваемого тепла, то вместо действительного значения водяного эквивалента W в расчетные формулы следует подставить значение W’ которое определяется следующим образом:
(2.34)
Знак минус (-) берется для горячей, а знак плюс (+) для холодной жидкости.
При таком способе учета внешних тепловых потерь все приведенные выше формулы для расчета конечных температур можно применять без какого-либо их изменения.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).