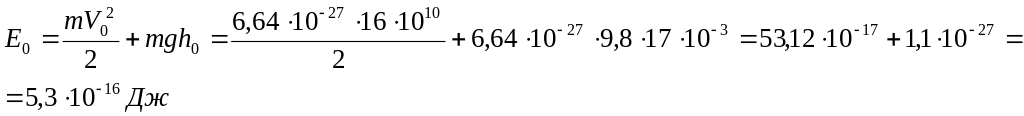Как найти начальную энергию частицы - Avtoru.top

Методика расчета

Энергия частицы

Начальная энергия рассчитывается по
следующей формуле:

Е₀– начальная энергия;

m – масса частицы;

V₀ – начальная
скорость.

m=4а.е.м.
=4·1,66·10^-27=6.64·10^-27кг;

Так
как скорость иона очень велика, его
потенциальную энергию можно было не
учитывать при вычислении полной энергии.

Ёмкость конденсатора

C=[Ф]

Величина емкости определяется геометрией
конденсатора, а также диэлектрическими
свойствами среды, заполняющей пространство
между обкладками.

Формула для емкости плоского конденсатора
следующая:

С – электроемкость плоского конденсатора;

₀ – диэлектрическая проницаемость
вакуума,

 -относительная диэлектрическая
проницаемость вещества заполняющего
зазор, =1 (воздух);

d – расстояние между
обкладками;

S – площадь пластины;

l – длина пластины;

Так как пластина имеет форму квадрата,
её площадь равна:

S=l²=0,4²=0,16
м²;

=7,074*10^-11Ф.

Разность потенциалов между пластинами
определяется по формуле:

U=[B]

Заряд определяется по формуле

Q=[Кл]

Вспомогательные
вычисления для построения графиков
зависимостей

На движущуюся в однородном электрическом
поле конденсатора частицу действуют
две силы:

(сила со стороны поля конденсатора) и

(сила тяжести). Поскольку частица заряжена
положительно, то она будет двигаться к
отрицательно заряженной пластине
конденсатора. Учитывая известные из
условия задачи направления координатных
осей, напишем уравнение для результирующей
сил

_{Сила, с которой электростатическое

поле конденсатора действует на помещенный

в него заряд}_q_{,

определяется по формуле, полученной из

закона Кулона:}

d – расстояние
между пластинами конденсатора, м

Сила тяжести вычисляется по формуле:

m – масса частицы, кг;

g – ускорение свободного
падения, g =9,8 м/с².

Сила, действующая на частицу в поле
конденсатора определяется по формуле:

F=[H]

Уравнение движения частицы в проекциях
на оси координат

х, у = [м]

Сила F действуют параллельно
оси ОY, поэтому проекция
ускорения на ось ОХ равна нулю:

.

Ускорение

а=а_х=а_у=
=[м/с²]

Полное ускорение:

,
т.к.

то

.

(по 2-му закону Ньютона)

Скорость

V=[м/с]

Общие уравнения для поступательного
движения выглядят следующим образом:

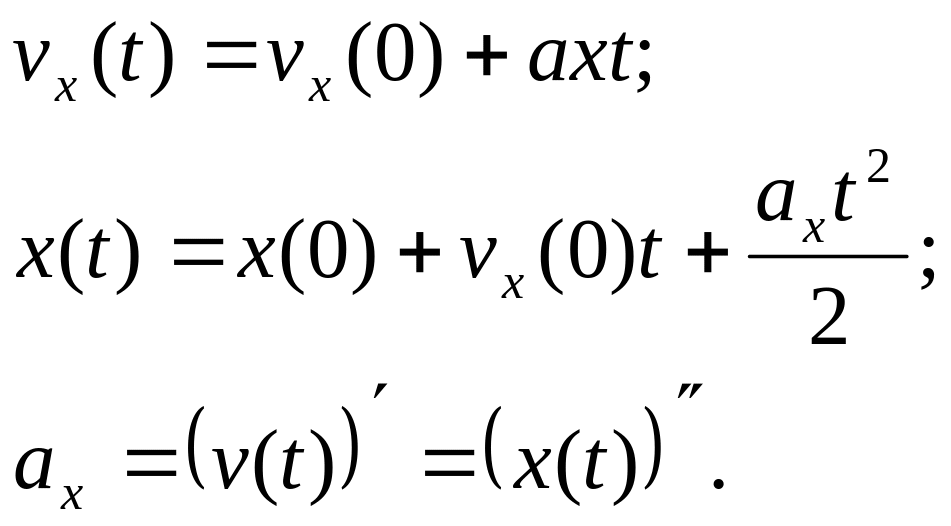
Для данного случая уравнения будут
выглядеть следующим образом:

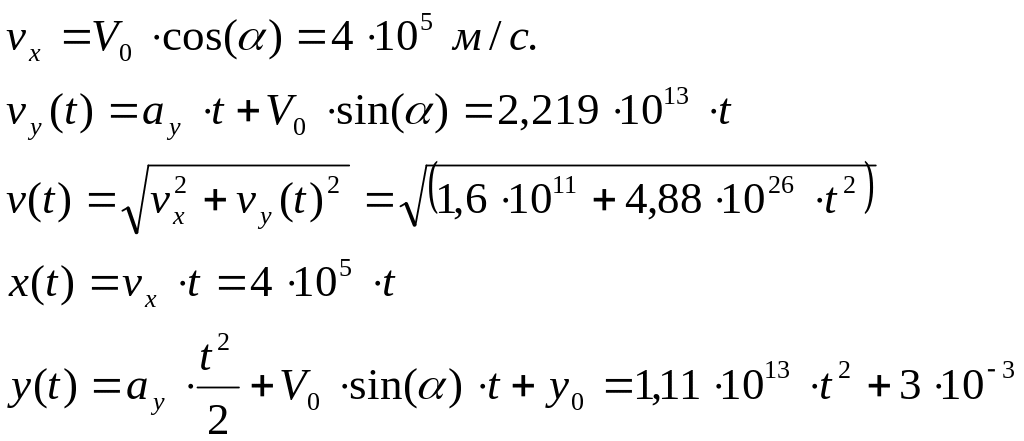
Касательное ускорение

Формула касательного ускорения выглядит
следующим образом:

,
подставляем в уравнение выше и получаем
следующее:

Время движения частицы

T=[c]

Максимальное перемещение по оси ОУ
является расстояние между пластинами.
Подставив его в уравнение движения
найдем максимальное время перемещения.

Т.к. время не может быть меньше нуля, то
t_max=

За время t_max=

частица пролетит по оси ОХ

и по оси ОУ

м.

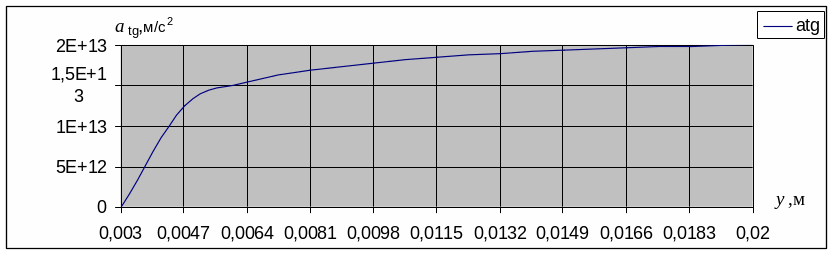
A(y) – зависимость тангенциального ускорения частицы от ее координаты “y”

Для построения графика найдём зависимость
касательного ускорения от y.

Из уравнения поступательного движения
имеем следующее соотношение времени
от перемещения:

Сделав следующую замену:

,
получим

.

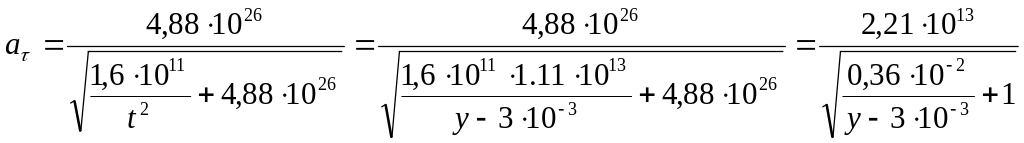
График зависимости касательного
ускорения

от координаты у

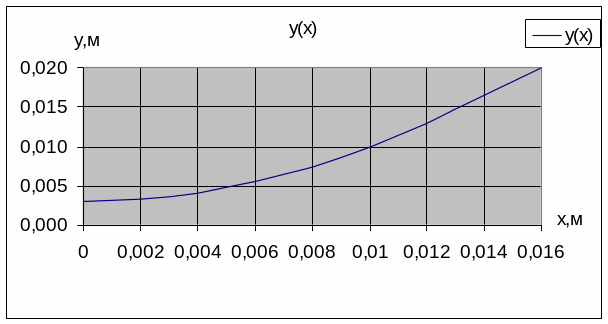
y(x) – зависимость координаты – “y”
частицы от ее положения “x”;

Для построения графика найдём зависимость
y от x.

Из уравнения поступательного движения
имеем следующее соотношение времени
от перемещения:

Через уравнение перемещения

,
заменив

,
получим зависимость

.

Анализ полученного
результата:

Движение частицы, после того, как она
влетела в заряженный конденсатор,
криволинейное;

На частицу практически не влияет сила
тяжести;

Между скоростью частицы и её координатой
существует прямо пропорциональная
зависимость;

Между тангенциальным ускорением частицы
и временем полёта её в конденсаторе
существует обратно пропорциональная
зависимость.

Данные, полученные мной по параметрам
конденсатора– вполне соответствуют
ёмкости конденсатора.

Вывод

В расчетно-графическом задании «Движение
заряженной частицы в электрическом
поле» рассматривалось движение иона
⁴He²⁺ в однородном
электрическом поле между обкладками
заряженного конденсатора. Для выполнения
задания ознакомился с устройством и
основными характеристиками конденсатора,
также изучил движение заряженной частицы
в однородном электрическом поле, а также
движение материальной точки по
криволинейной траектории и рассчитал
необходимые по заданию параметры частицы
и конденсатора:

Начальная кинетическая энергия:

C – ёмкость конденсатора;
C=7,074*10^-11 Ф.

Q – заряд ;

U –разность потенциалов
между пластинами;

Построенные графики отображают
зависимости: y(x)
– зависимость координаты “y”
частицы от ее положения “x”;
a_(y)
– зависимость тангенциального ускорения
частицы от ее координаты “y”
при этом учтено, что время полета конечно,
т.к. они заканчивает свое движение на
отрицательно заряженной пластине
конденсатора (на верхней пластине).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
#
#
02.04.20152.21 Mб29РГР №1.doc
#
#
#
#

Источник

Задание.

Ион ⁴⁸BF₂⁺
влетает в плоский конденсатор с начальной скоростью 500
км/с, под углом 10°
к положительно заряженной пластине на расстоянии 12 мм от отрицательно
заряженной пластины. Длина пластины (она имеет квадратную форму) 40 см, разность
потенциалов между пластинами 20 кВ, емкость конденсатора 0,1 нВ . Определить
начальную энергию частицы, заряд на пластинах конденсатора, его энергию и
расстояние между пластинами конденсатора. Построить графики а_n(t) — зависимость нормального ускорения частицы от времени
полета в конденсаторе, V(x) — зависимость скорости
частицы от ее координаты “x”.

Исходные данные.

Параметры частицы:

M_r=48

q=1,6∙10^-19Кл

v₀=500
км/с=5*10⁵ м/с

h₀=12
мм=0,012 м

a₊=10°

Параметры конденсатора:

d=12мм=0,012м

l=50cм=0,5м

U=20 кВ=2*10⁴В

С=0,1 нВ=0,1*10^-9
В

Основные теоретические положения.

Конденсатор — накопитель электрического
заряда.

Конденсатор представляет собой два близко расположенных
проводника (в данной задаче это тонкие пластины), разделенных слоем
диэлектрика.

Образующие конденсатор проводники называют обкладками
конденсатора.

Емкость — характеристика
конденсатора, количественная мера его способности удерживать электрический
заряд, под которой понимают величину, пропорциональную заряду q
и обратно пропорциональную разности потенциалов между обкладками U:

;

Энергией
заряженного конденсатора W называется полная
энергия системы двух проводников и вычисляется по формуле:

Энергия частицы,
обусловленная ее движением (скоростью), называется кинетической энергией
и вычисляется по формуле:

где m — масса частицы; v — скорость движения частицы.

На заряженную частицу со
стороны поля конденсатора действует сила:

где q — заряд конденсатора;-напряженность поля конденсатора.

Влетая в плоский
конденсатор, частица движется криволинейно и неравномерно.

Ускорение — харрактеристика
неравномерного движения; определяет быстроту изменения
скорости по модулю и направлению.

Составляющие
ускорения:

·
Тангенциальная — харрактеризует
быстроту изменения скорости по модулю

(направлена
по касательной к траектории) и обозначается а_t:

·
нормальная — харрактеризует быстроту изменения
скорости по направлению

(направлена к центру
кривизны траектории) и определяется по формуле:

где R —
радиус кривизны траектории.

Полное ускорение при
криволинейном движении — геометрическая сумматангенциальной и
нормальной составляющих

Методика расчета.

1.
Начальная кинетическая энергия частицы.

Начальная кинетическая энергия частицы определяется по
формуле:

где v₀-начальная скорость частицы,

m — масса иона ⁴⁸BF₂⁺,
которая вычисляется по формуле

Источник

Если скорость релятивистской частицы меньше скорости света, то она называется массовой. Её собственная энергия, то есть энергия при (v=0):
(boxed{E_0=m_0cdot c^2}), ((1))
где (m_0) — масса покоя частицы, (E_0) — энергия покоя частицы.
Масса движущейся релятивистской частицы:
(boxed{m=frac{m_0}{sqrt{1-frac{v^2}{c^2}}}}). ((2))
Полная (релятивистская) энергия, или энергия свободной (невзаимодействующей) движущейся релятивистской частицы (сформулировал А. Эйнштейн):
(boxed{E=frac{m_0 c^2}{sqrt{1-frac{v^2}{c^2}}}}). ((3))
Кинетическая энергия массовой частицы:
(boxed{E_k=E-E_0}). ((4))
Импульс частицы:
(boxed{vec{p}=frac{m_0 vec{v}}{sqrt{1-frac{v^2}{c^2}}}}). ((5))
Если скорость частицы равна скорости света, то такую частицу называют безмассовой (фотон и нейтрино). В таком случае энергия и импульс свободной частицы связаны соотношением:
(boxed{E^2-p^2c^2=0}). ((6))
Таким образом, для всех свободных частиц в любой инерциальной системе можно записать:
(boxed{E^2-p^2c^2=m_0^2c^4}). ((7))

Источник

Релятивистская динамика

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: полная энергия, связь массы и энергии, энергия покоя.

В классической динамике мы начали с законов Ньютона, потом перешли к импульсу, а после него — к энергии. Здесь мы ради простоты изложения поступим ровно наоборот: начнём с энергии, затем перейдём к импульсу и закончим релятивистским уравнением движения — модификацией второго закона Ньютона для теории относительности.

Релятивистская энергия

Предположим, что изолированное тело массы покоится в данной системе отсчёта. Одно из самых впечатляющих достижений теории относительности — это знаменитая формула Эйнштейна:

$E=mc^{2}$ (1)

Здесь — энергия тела, — скорость света в вакууме. Поскольку тело покоится, энергия , вычиляемая по формуле (1), называется энергией покоя.

Формула (1) утверждает, что каждое тело само по себе обладает энергией — просто потому, что оно существует в природе. Образно говоря, природа затратила определённые усилия на то, чтобы «собрать» данное тело из мельчайших частиц вещества, и мерой этих усилий служит энергия покоя тела. Энергия эта весьма велика; так, в одном килограмме вещества заключена энергия

$E=1cdot (3cdot 10^{8})^{2}=9cdot 10^{16}$ Дж.

Интересно, какое количество топлива нужно сжечь, чтобы выделилось столько энергии? Возьмём, например, дерево. Его удельная теплота сгорания равна $q=10^{7}$ Дж/кг, поэтому находим: $m= E/q= 9cdot 10^{9}$ кг. Это девять миллионов тонн!

Ещё для сравнения: такую энергию единая энергосистема России вырабатывает примерно за десять дней.

Почему столь грандиозная энергия, содержащаяся в теле, до сих пор оставалась нами незамеченной? Почему в нерелятивистских задачах, связанных с сохранением и превращением энергии, мы не учитывали энергию покоя? Скоро мы ответим на этот вопрос.

Поскольку энергия покоя тела прямо пропорциональна его массе, изменение энергии покоя на величину Delta E приводит к изменению массы тела на

$Delta m= frac{Delta displaystyle E}{displaystyle c^{displaystyle 2}}$ .

Так, при нагревании тела возрастает его внутренняя энергия, и, стало быть, масса тела увеличивается! В повседневной жизни мы не замечаем этого эффекта ввиду его чрезвычайной малости. Например, для нагревания воды массой m= 1 кг на $Delta t= 100^{circ}C$ (удельная теплоёмкость воды равна $c_{b}= 4200 J/(kgcdot^{circ}C)$ ) ей нужно передать количество теплоты:

$Q= c_{b}mDelta t= 4,2cdot 10^{5}$ Дж.

Увеличение массы воды будет равно:

$Delta m= frac{Q}{c^{2}}= frac{4,2cdot 10^{5}}{9cdot 10^{16}}approx 4,7cdot 10^{-12}$ кг.

Столь ничтожное изменение массы невозможно заметить на фоне погрешностей измерительных приборов.

Формула ( 1) даёт энергию покоящегося тела. Что изменится, если тело движется?

Снова рассмотрим неподвижную систему отсчёта и систему {K} , движущуюся относительно со скоростью upsilon . Пусть тело массы покоится в системе {K} ; тогда энергия тела в системе {K} есть энергия покоя, вычисляемая по формуле ( 1). Оказывается, при переходе в систему энергия преобразуется так же, как и время — а именно, энергия тела в системе , в которой тело движется со скоростью upsilon , равна:

$E= frac{mc^{2}}{sqrt{displaystyle 1-frac{upsilon ^{displaystyle 2}}{c^{displaystyle 2}}}}$ ( 2)

Формула ( 2) была также установлена Эйнштейном. Величина — это полная энергия движущегося тела. Поскольку в данной формуле $mc^{2}$ делится на «релятивистский корень», меньший единицы, полная энергия движущегося тела превышает энергию покоя. Полная энергия будет равна энергии покоя только при .

Выражение для полной энергии ( 2) позволяет сделать важные выводы о возможных скоростях движения объектов в природе.

1. Каждое массивное тело обладает определённой энергией, поэтому необходимо выполнение неравенства

$1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}> 0$ .

Оно означает, что : скорость массивного тела всегда меньше скорости света.

2. В природе существуют безмассовые частицы (например, фотоны), несущие энергию. При подстановке m= 0 в формулу ( 2) её числитель обращается в нуль. Но энергия-то фотона ненулевая!

Единственный способ избежать здесь противоречия — это принять, что безмассовая частица обязана двигаться со скоростью света. Тогда и знаменатель нашей формулы обратится в нуль, так что формула ( 2) попросту откажет. Нахождение формул для энергии безмассовых частиц не входит в компетенцию теории относительности. Так, выражение для энергии фотона устанавливается в квантовой физике.

Интуитивно чувствуется, что полная энергия ( 2) состоит из энергии покоя и собственно «энергии движения», т. е. кинетической энергии тела. При малых скоростях движения это показывается явным образом. Используем приближённые формулы, справедливые при :

$sqrt{1-alpha }approx 1-frac{alpha }{2}$ ( 3)
$frac{1}{1-alpha }approx 1+alpha$ ( 4)

С помощью этих формул последовательно получаем из ( 2):

$E= frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}approx frac{displaystyle mc^{displaystyle 2}}{1-frac{displaystyle 1}{displaystyle 2}frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}approx mc^{2}(1+frac{displaystyle 1}{displaystyle 2}frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}})= mc^{2}+frac{displaystyle mupsilon ^{displaystyle 2}}{displaystyle 2}$ ( 5)

Таким образом, при малых скоростях движения полная энергия сводится просто к сумме энергия покоя и кинетической энергии. Это служит мотивировкой для определения понятия кинетической энергии в теории относительности:

$E_{K}=frac{mc^{2}}{sqrt{1-frac{upsilon ^{2}}{c^{2}}}}-mc^{2}$ . ( 6)

При формула ( 6) переходит в нерелятивистское выражение $E_{K}= mupsilon ^{2}/2$ .

Теперь мы можем ответить на заданный выше вопрос о том, почему до сих пор не учитывалась энергия покоя в нерелятивистских энергетических соотношениях. Как видно из ( 5), при малых скоростях движения энергия покоя входит в полную энергию в качестве слагаемого. В задачах, например, механики и термодинамики изменения энергии тел составляют максимум несколько миллионов джоулей; эти изменения столь незначительны по сравнению с энергиями покоя рассматриваемых тел, что приводят к микроскопическим изменениям их масс. Поэтому с высокой точностью можно считать, что суммарная масса тел не меняется в ходе механических или тепловых процессов. В результате суммы энергий покоя тел в начале и в конце процесса попросту сокращаются в обеих частях закона сохранения энергии!

Но такое бывает не всегда. В других физических ситуациях изменения энергии тел могут приводить к более заметным изменениям суммарной массы. Мы увидим, например, что в ядерных реакциях отличия масс исходных и конечных продуктов обычно составляют доли процента.Скажем, при распаде ядра урана $_{92}^{235}{cup }$ суммарная масса продуктов распада примерно на 0,1% меньше массы исходного ядра. Эта одна тысячная доля массы ядра высвобождается в виде энергии, которая при взрыве атомной бомбы способна уничтожить город.

При неупругом столкновении часть кинетической энергии тел переходит в их внутренюю энергию. Релятивистский закон сохранения полной энергии учитывает этот факт: суммарная масса тел после столкновения увеличивается!

Рассмотрим в качестве примера два тела массы , летящих навстречу друг другу с одинаковой скоростью 3c/5 . В результате неупругого столкновения образуется тело массы , скорость которого равна нулю по закону сохранения импульса (об этом законе речь впереди). Согласно закону сохранения энергии получаем:

$frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{(displaystyle 3c/5)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}+frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{(displaystyle 3c/5)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= Mc^{2}$ ,

$2cdot frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-(frac{displaystyle 3}{displaystyle 5})^{displaystyle 2}}}= Mc^{2}$ ,

$frac{displaystyle 2m}{displaystyle 4/5}= M$ ,

$M= frac{displaystyle 5}{displaystyle 2}m$ .

Мы видим, что, M> 2m — масса образовавшегося тела превышает сумму масс тел до столкновения. Избыток массы, равный m/2 , возник за счёт перехода кинетической энергии сталкивающихся тел во внутреннюю энергию.

Релятивистский импульс.

Классическое выражение для импульса не годится в теории относительности — оно, в частности, не согласуется с релятивистским законом сложения скоростей. Давайте убедимся в этом на следующем простом примере.

Пусть система {K} движется относительно системы со скоростью v = c/2 (рис. 1). Два тела массы в системе {K} летят навстречу друг другу с одинаковой скоростью {u} . Происходит неупругое столкновение.

Рис. 1. К закону сохранения импульса

В системе {K} тела после столкновения останавливаются. Давайте, как и выше, найдём массу образовавшегося тела:

$Mc^{2}= 2frac{displaystyle mc^{displaystyle 2}}{sqrt{displaystyle 1-frac{(displaystyle c/2)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= frac{displaystyle 2mc^{displaystyle 2}}{sqrt{displaystyle 1-(frac{displaystyle 1}{displaystyle 4})^{displaystyle 2}}}= frac{displaystyle 4mc^{displaystyle 2}}{sqrt{displaystyle 3}}$ ,

откуда

$M= frac{displaystyle 4m}{sqrt{displaystyle 3}}$ .

Теперь посмотрим на процесс столкновения с точки зрения системы . До столкновения левое тело имеет скорость:

$u_{1}= frac{displaystyle upsilon +{displaystyle u}$ .

Правое тело имеет скорость:

$u_{2}= frac{displaystyle upsilon -{displaystyle u}$ .

Нерелятивистский импульс нашей системы до столкновения равен:

$mu_{1}-mu_{2}= frac{displaystyle 4mc}{displaystyle 5}$ .

После столкновения получившееся тело массы двигается со скоростью .
Его нерелятивистский импульс равен:

$Mupsilon = frac{displaystyle 4m}{sqrt{displaystyle 3}}frac{displaystyle c}{displaystyle 2}= frac{displaystyle 2m}{sqrt{displaystyle 3}}$ .

Как видим, $mu_{1}-mu_{2}neq Mupsilon$ , то есть нерелятивистский импульс не сохраняется.

Оказывается, правильное выражение для импульса в теории относительности получается делением классического выражения на «релятивистский корень»: импульс тела массы , двигающегося со скоростью , равен:

$vec{p}= frac{displaystyle mvec{displaystyle upsilon }}{sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}$ . 7

Давайте вернёмся к только что рассмотренному примеру и убедимся, что теперь с законом сохранения импульса всё будет в порядке.

Импульс системы до столкновения:

$p_{before}= frac{displaystyle mu_{displaystyle 1}}{sqrt{displaystyle 1-frac{displaystyle u_{displaystyle 1}^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}- frac{displaystyle mu_{displaystyle 2}}{sqrt{displaystyle 1-frac{displaystyle u_{displaystyle 2}^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= frac{displaystyle m(displaystyle 4c/5)}{displaystyle sqrt{displaystyle 1-frac{(displaystyle 4c/5)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}-0= frac{displaystyle 4mc/5}{displaystyle 3/5}= frac{displaystyle 4mc}{displaystyle 3}$ .

Импульс после столкновения:

$p_{after}= frac{displaystyle displaystyle Mupsilon }{sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= frac{displaystyle Mc/2}{sqrt{displaystyle 1-frac{(displaystyle c/2)^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}=( frac{displaystyle 4m/sqrt{displaystyle 3})(displaystyle c/2)}{sqrt{displaystyle 3/2}}= frac{displaystyle 4mc}{displaystyle 3}$

Вот теперь всё правильно: $p_{before}= p_{after}$ !

Связь энергии и импульса.

Из формул ( 2) и ( 7) можно получить замечательное соотношение между энергией и импульсом в теории относительности. Возводим обе части этих формул в квадрат:

$E^{2}= frac{displaystyle m^{displaystyle 2}c^{displaystyle 4}}{1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}$ , $p^{2}= frac{displaystyle m^{displaystyle 2}upsilon ^{displaystyle 2}}{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}$

Преобразуем разность:

$E^{2}-p^{2}c^{2}= frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 4}}{1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}-frac{displaystyle m^{displaystyle 2}upsilon ^{displaystyle 2}c^{displaystyle 2}}{1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}= frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}(displaystyle c^{displaystyle 2}-displaystyle upsilon ^{displaystyle 2})}{frac{displaystyle c^{displaystyle 2}-displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}= m^{2}c^{4}$

Это и есть искомое соотношение:

$E^{2}-p^{2}c^{2}= m^{2}c^{4}$ . ( 8)

Данная формула позволяет выявить простую связь между энергией и импульсом фотона. Фотон имеет нулевую массу и движется со скоростью света. Как уже было замечено выше, сами по себе энергия и импульс фотона в СТО найдены быть не могут: при подстановке в формулы ( 2) и ( 7) значений m=0 и мы получим нули в числителе и знаменателе. Но зато с помощью ( 8) легко находим: $E^{2}-p^{2}c^{2}= 0$ , или

E= pc ( 9)

В квантовой физике устанавливается выражение для энергии фотона, после чего с помощью формулы ( 9) находится его импульс.

Релятивистское уравнение движения.

Рассмотрим тело массы , движущееся вдоль оси под действием силы . Уравнение движения тела в классической механике — это второй закон Ньютона: ma= F . Если за бесконечно малое время приращение скорости тела равно , то , и уравнение движения запишется в виде:

$mfrac{displaystyle dupsilon }{displaystyle dt}= F$ . ( 10)

Теперь заметим, что — изменение нерелятивистского импульса тела. В результате получим «импульсную» форму записи второго закона Ньютона — производная импульса тела по времени равна силе, приложенной к телу:

$frac{dp}{dt}= F$ . ( 11)

Все эти вещи вам знакомы, но повторить никогда не помешает

Классическое уравнение движения — второй закон Ньютона — является инвариантным относительно преобразований Галилея, которые в классической механике описывают переход из одной инерциальной системы отсчёта в другую (это означает, напомним, что при указанном переходе второй закон Ньютона сохраняет свой вид). Однако в СТО переход между инерциальными системами отсчёта описывается преобразованиями Лоренца, а относительно них второй закон Ньютона уже не является инвариантным. Следовательно, классическое уравнение движения должно быть заменено релятивистским, которое сохраняет свой вид под действием преобразований Лоренца.

То, что второй закон Ньютона ( 10) не может быть верным в СТО, хорошо видно на следующем простом примере. Допустим, что к телу приложена постоянная сила. Тогда согласно классической механике тело будет двигаться с постоянным ускорением; скорость тела будет линейно возрастать и с течением времени превысит скорость света. Но мы знаем, что на самом
деле это невозможно.

Правильное уравнение движения в теории относительности оказывается совсем не сложным.
Релятивистское уравнение движения имеет вид ( 11), где p — релятивистский импульс:

$frac{displaystyle d(frac{displaystyle mupsilon }{sqrt{displaystyle 1-upsilon ^{displaystyle 2}/displaystyle c^{displaystyle 2}}})}{displaystyle dt}= F$ . ( 12)

Производная релятивистского импульса по времени равна силе, приложенной к телу.

В теории относительности уравнение ( 12) приходит на смену второму закону Ньютона.

Давайте выясним, как же в действительности будет двигаться тело массы m под действием постоянной силы . При условии из формулы ( 12) получаем:

$frac{displaystyle mupsilon }{displaystyle sqrt{displaystyle 1-frac{displaystyle upsilon ^{displaystyle 2}}{displaystyle c^{displaystyle 2}}}}= Ft$ .

Остаётся выразить отсюда скорость:

$upsilon = frac{displaystyle cFt}{sqrt{displaystyle F^{displaystyle 2}t^{displaystyle 2}+m^{displaystyle 2}c^{displaystyle 2}}}$ . ( 13)

Посмотрим, что даёт эта формула при малых и при больших временах движения.
Пользуемся приближёнными соотношениями при :

$sqrt{displaystyle 1+alpha }approx 1+frac{displaystyle alpha }{displaystyle 2}$ , ( 14)

$frac{displaystyle 1}{displaystyle 1+alpha }approx 1-alpha$ . ( 15)

Формулы ( 14) и ( 15) отличаются от формул ( 3) и ( 4) только лишь знаком в левых частях. Очень рекомендую вам запомнить все эти четыре приближённых равенства — они часто используются в физике.

Итак, начинаем с малых времён движения. Преобразуем выражение ( 13) следующим образом:

$upsilon = frac{displaystyle cFt}{displaystyle mcsqrt{displaystyle 1+frac{displaystyle F^{displaystyle 2}t^{displaystyle 2}}{displaystyle m^{displaystyle 2}c^{displaystyle 2}}}}$ .

При малых имеем:

$frac{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}ll 1$ .

Последовательно пользуясь нашими приближёнными формулами, получим:

$upsilon approx frac{displaystyle cFt}{displaystyle mc(1+frac{displaystyle 1}{displaystyle 2}frac{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}})}approx frac{displaystyle Ft}{displaystyle m}(1-frac{F^{displaystyle 2}t^{displaystyle 2}}{displaystyle 2m^{displaystyle 2}displaystyle c^{displaystyle 2}})$ .

Выражение в скобках почти не отличается от единицы, поэтому при малых имеем:

$upsilon approx frac{Ft}{m}= at$ .

Здесь a= F/m — ускорение тела. Мы получили результат, хорошо известный нам из классической механики: скорость тела линейно растёт со временем. Это и не удивительно — при малых временах движения скорость тела также невелика, поэтому мы можем пренебречь релятивистскими эффектами и пользоваться обычной механикой Ньютона.

Теперь переходим к большим временам. Преобразуем формулу ( 13) по-другому:

$upsilon approx frac{displaystyle cFt}{displaystyle Ftsqrt{displaystyle 1+frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}}}= frac{displaystyle c}{sqrt{1+frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}{displaystyle F^{displaystyle 2}t^{displaystyle 2}}}}$ .

При больших значениях имеем:

$frac{displaystyle m^{displaystyle 2}displaystyle c^{displaystyle 2}}{displaystyle F^{displaystyle 2}displaystyle t^{displaystyle 2}}ll 1$ ,

и тогда:

$upsilon approx frac{c}{1+frac{1}{2}frac{m^{2}c^{2}}{F^{2}t^{2}}}approx c(1-frac{m^{2}c^{2}}{2F^{2}t^{2}})$ .

Хорошо видно, что при скорость тела upsilon неуклонно приближается к скорости света , но всегда остаётся меньше — как того и требует теория относительности.

Зависимость скорости тела от времени, даваемая формулой ( 13), графически представлена на рис. 2.

Рис. 2. Разгон тела под действием постоянной силы

Начальный участок графика — почти линейный; здесь пока работает классическая механика. Впоследствии сказываются релятивистские поправки, график искривляется, и при больших временах наша кривая асимптотически приближается к прямой .

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Релятивистская динамика» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Методика расчета

A(y) – зависимость тангенциального ускорения частицы от ее координаты “y”

Релятивистская динамика

Релятивистская энергия

Релятивистский импульс.

Связь энергии и импульса.

Релятивистское уравнение движения.

Не пропустите также: