- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
Что такое полином? Полином — это степенная функция y=ax2+bx+c (полином второй степени) и y=ax3+bx2+cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.
У полинома второй степени y=ax2+bx+c один экстремум (на графике ниже 1 максимум).
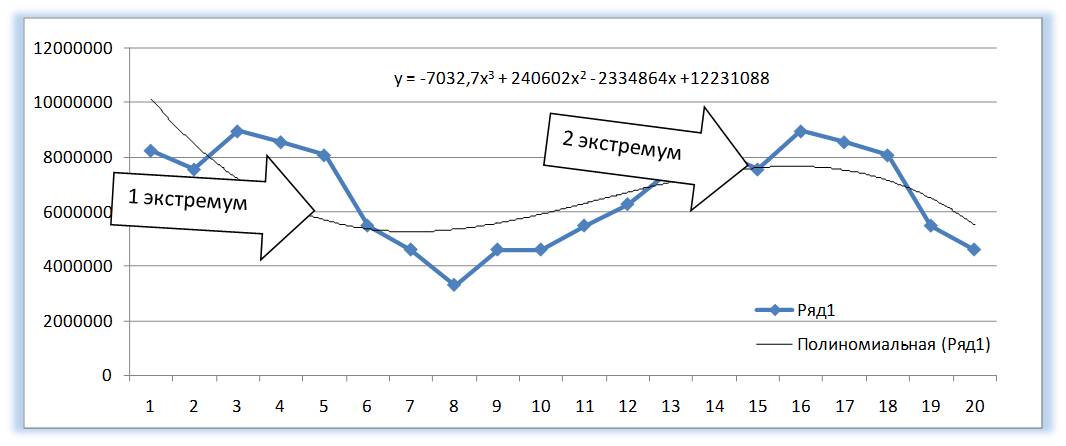
У Полинома третьей степени y=ax3+bx2+cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Как рассчитать значения полинома в Excel?
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
1-й способ расчета полинома — с помощью графика
Выделяем ряд со значениями и строим график временного ряда.
На график добавляем полином 6-й степени.
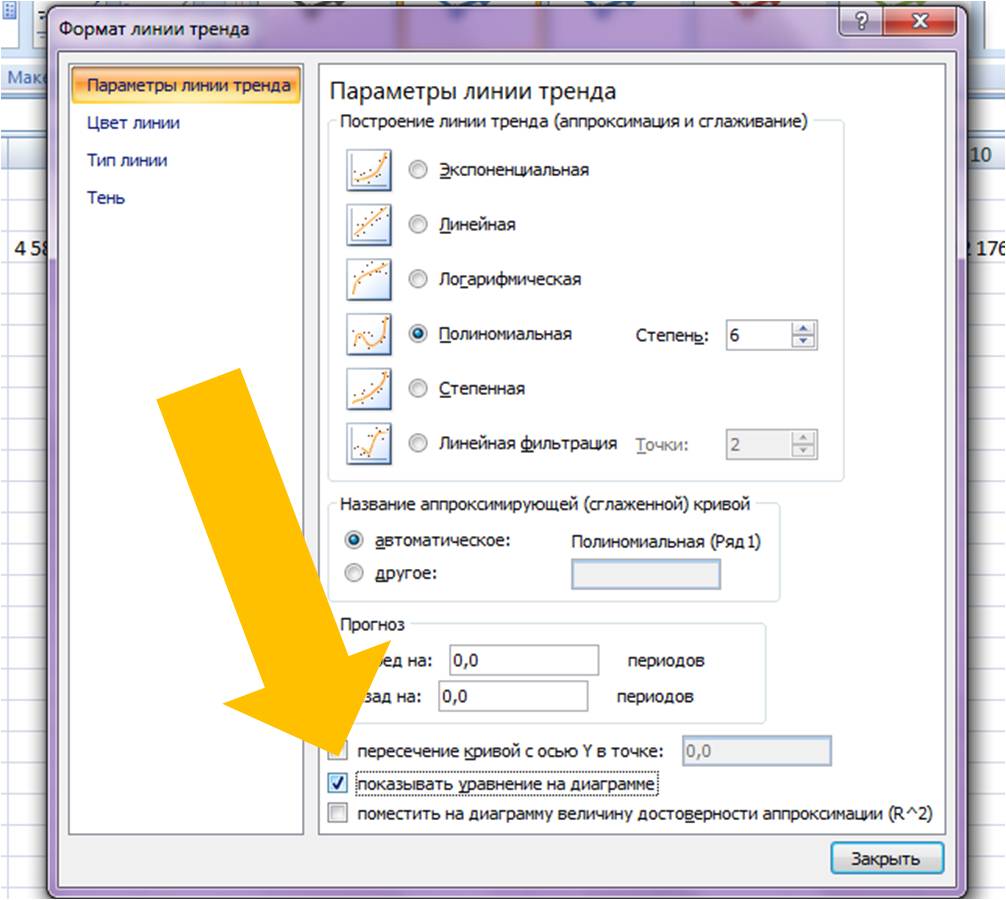
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
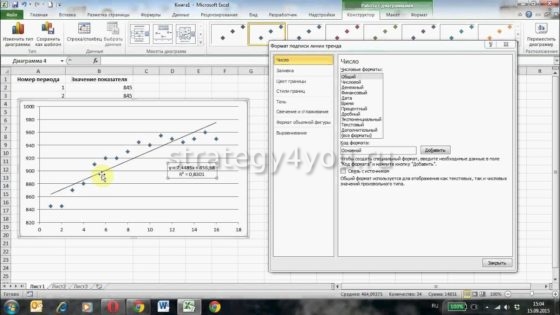
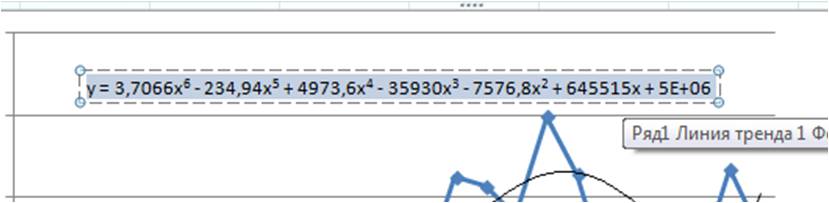
После этого уравнение выводится на график y = 3,7066x6 — 234,94x5 + 4973,6x4 — 35930x3 — 7576,8x2 + 645515x + 5E+06. Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
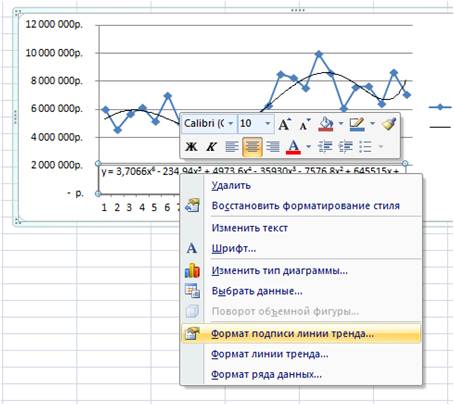
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
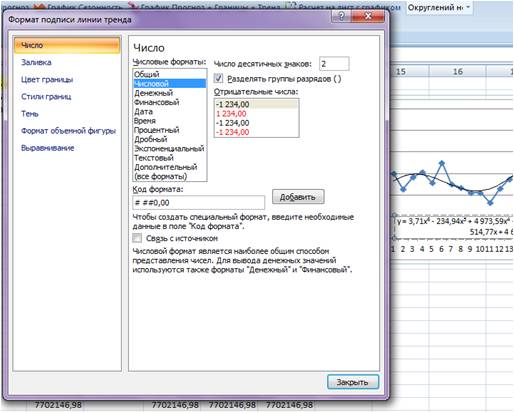
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
Получаем уравнение полинома в читаемом формате:
y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35
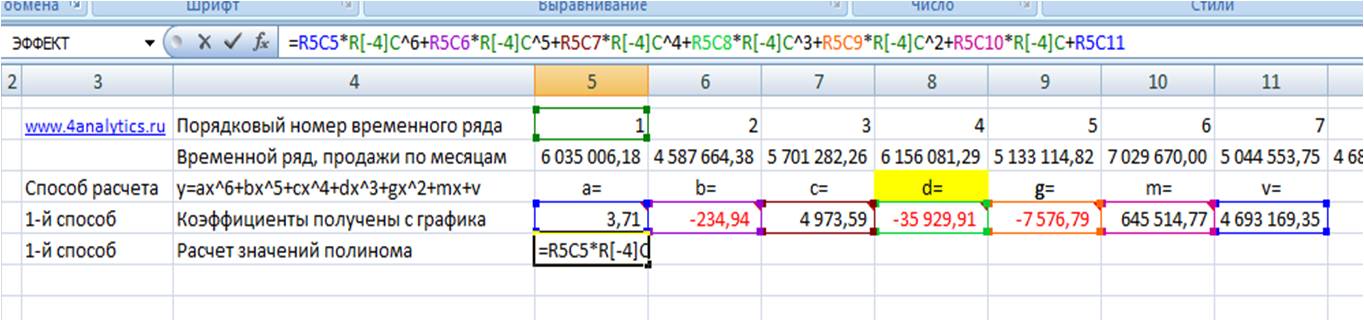
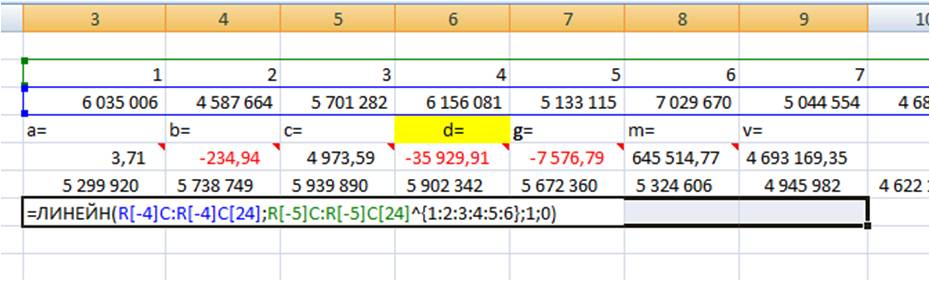
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x6 — 234,94x5 + 4 973,59x4 — 35 929,91x3 — 7 576,79x2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
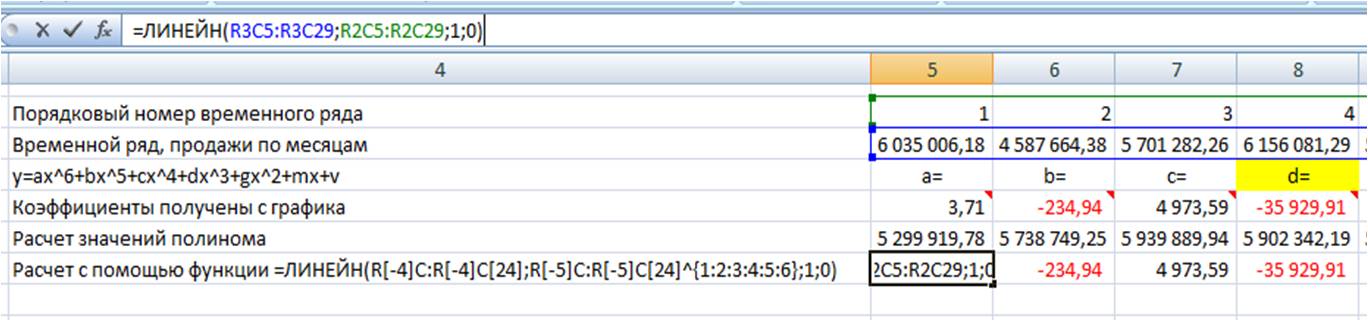
Получаем следующего вида формулу:
=ЛИНЕЙН(R[-4]C:R[-4]C[24];R[-5]C:R[-5]C[24];1;0),
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.
Для этого в часть формулы с «известными значениями x» вписываем степень полинома:
- ^{1:2:3:4:5:6} — для расчета коэффициентов полинома 6-й степени
- ^{1:2:3:4:5} — для расчета коэффициентов полинома 5-й степени
- ^{1:2} — для расчета коэффициентов полинома 2-й степени
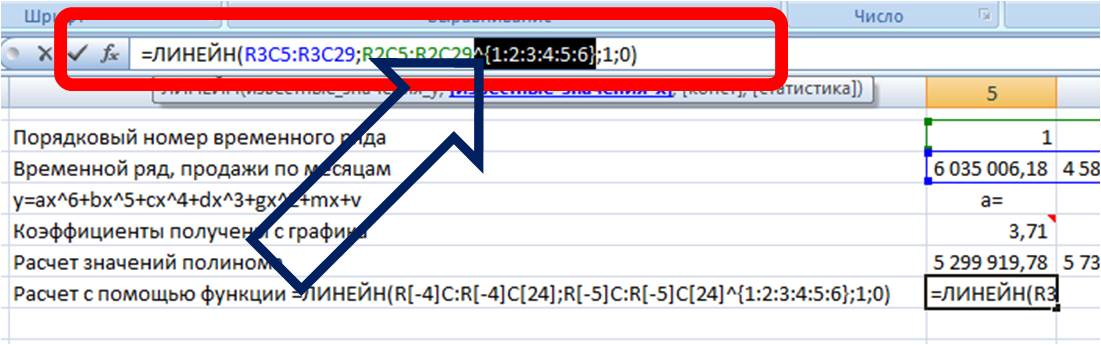
Получаем формулу следующего вида:
=ЛИНЕЙН(R[-4]C:R[-4]C[24]; R[-5]C:R[-5]C[24]^{1:2:3:4:5:6}; 1; 0)
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v
Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:
1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:
2. Нажать на клавишу F2
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)
Получаем 7 коэффициентов полиномиального тренда 6-й степени.
Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.
Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3]^6+R3C8*RC[-3]^5+R4C8*RC[-3]^4+R5C8*RC[-3]^3+R6C8*RC[-3]^2+R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
Скачать файл с примером расчета значений полинома.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
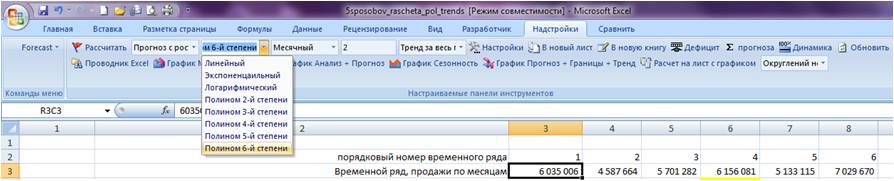
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
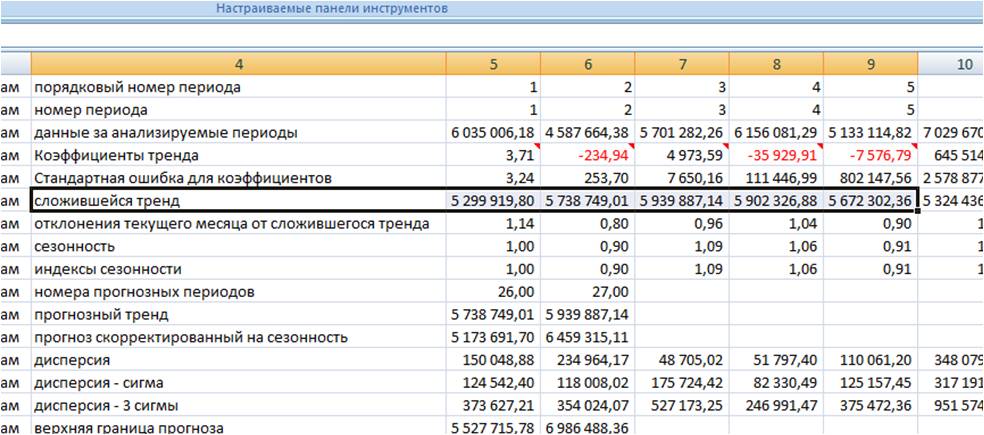
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
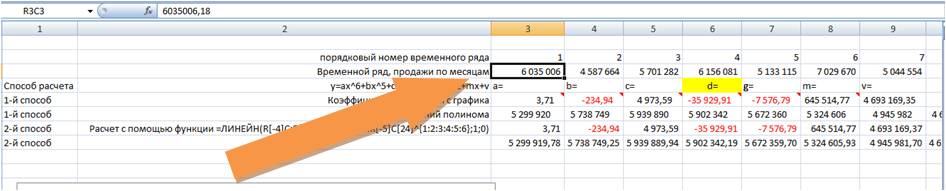
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
Скачать файл с примером расчета значений полинома.
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Функции и графики
Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. ФУНКЦИИ И ГРАФИКИ. — М: МЦНМО, 2005.
§ 7. Многочлены
1. Что такое многочлен. Если взять несколько степенных функций, например,
f(x) = x2, g(x) = x5, q(x) = x3,
помножить их на какие-нибудь коэффициенты, например,
3f(x) = 3x2, –g(x) = –x5, 2,5q(x) = 2,5x3,
и сложить, то получится новая функция
R(x) = 3x2 – x5 + 2,5x3.
Выражение 3x2 – x5 + 2,5x3, как вы знаете, называется многочленом. В общем виде многочлен записывается и обозначается так:
Qn(x) = anxn + an – 1xn – 1 + an – 2xn – 2 + … + a1x + a0.
Функцию, задаваемую формулой вида
y = anxn + an – 1xn – 1 + … + a1x + a0,
тоже называют многочленом.
Многочлены — очень важный класс функций. Это связано, прежде всего, с тем, что значения многочлена просто вычисляются: для этого над аргументом нужно произвести только операции двух видов, самых простых — сложение и умножение. Поэтому функция
y = Qn(x) имеет еще одно название — целая рациональная функция.
Формула, задающая целую рациональную функцию, не обязательно имеет форму многочлена. Например, при вычислении значений функции
над аргументом производятся только сложение и умножение (деление на число 2, а не на аргумент, не считается, так как его можно заменить умножением на
). Поэтому F(x) является целой рациональной функцией и, как и всякую такую функцию, ее можно представить в виде многочлена:
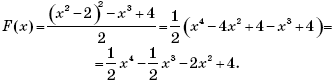
Функция G(x) = (x – 1)(x – 2)(x – 3)(x – 4) — тоже целая рациональная, и ее тоже можно представить в виде многочлена: раскрыть скобки, привести подобные члены и расположить их в порядке убывания степеней.
Упражнения
7-1. Определите степени многочленов
1, задающих следующие целые рациональные функции:
а) 155x2 – 3x; б) y = (x – 1)(x3 + 5x – 3);
в) (x – 1)(x3 + 5x – 3)5;
г) (x – 1)(x2 – 1)(x3 – 1)(x4 – 1)∙…∙(x100 – 1).
7-2. Чему равны свободные члены в многочленах а)–г)?
7-3. Чему равен член с x в первой степени в многочленах (x + 1)n?
2. О графиках многочленов. С графиками простейших многочленов вы уже встречались и умеете их строить. Так, график многочлена первой степени — линейной функции
y = kx + b — это прямая линия, многочлена второй степени
y = ax2 + bx + c — парабола. Знакомые вам графики многочленов высоких степеней для случая y = xn (то есть не многочленов, а одночленов) тоже по существу однотипны, вернее, «двутипны» — для четных n и для нечетных n.
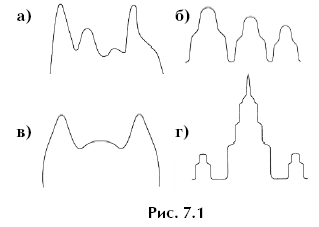
А вот графики многочленов общего вида очень разнообразны и могут иметь самую причудливую форму. Например, графиком многочлена можно «нарисовать» горный пейзаж, или трех матрешек, или кошачьи ушки и даже силуэт здания Московского университета (рис. 7.1). Справедливо следующее утверждение.
Утверждение. Любая непрерывная кривая, имеющая на некотором промежутке a ≤ x ≤ b
с каждой из прямых, параллельных Oy, в точности одну общую точку, может быть приближенно задана как график функции y= Pn(x), где Pn(x) — многочлен.
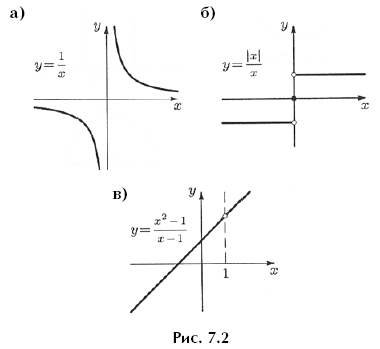
Однако есть два ограничения, указывающие на то, каким не может быть график многочлена. Во-первых, график многочлена не может иметь «разрывов»
2 — ни таких, как у графика
(рис. 7.2,а), ни таких, как у графика
(рис. 7.2,б), ни даже таких, как на графике функции
(рис. 7.2,в).
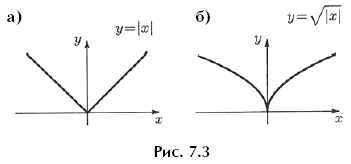
Во-вторых, у графика многочлена не может быть «углов»
3, таких, как у графика y = | x | (рис. 7.3,а) или графика
(рис. 7.3,б).
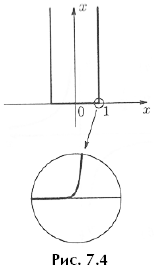
Замечание. Конечно, эти ограничения относятся только к точным графикам, то есть к некоторой идеализации, которую невозможно реализовать. А «с точностью до ширины линии» и то, и другое возможно. Например, если мы попытаемся изобразить график
y = x1000 от 0 до 1, то получим картинку как на рисунке 7.4, где около точки (1; 0)
придется нарисовать прямой угол. Однако если мы рассмотрим этот участок графика «под микроскопом», то вместо излома увидим закругление.
Итак, несмотря на разнообразие, все графики многочленов имеют важные общие свойства: каждый такой график можно начертить «одним росчерком пера» (то есть он является непрерывной кривой) и не поворачивая карандаша резко, сразу на какой-то угол (то есть кривая графика должна быть плавной).
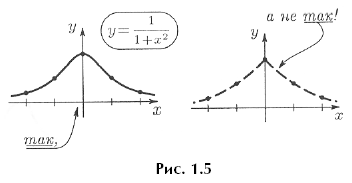
Есть еще общее свойство у графиков многочленов: такой график не ограничен по вертикали, то есть он не может поместиться в горизонтальной «полоске» (в отличие, например, от графика — см. рис. 1.5), даже если полоска будет очень широкой.
Все определит старший член: при n четном обе ветви идут сколь угодно высоко, если число an (коэффициент при xn) положительно, или сколь угодно низко, если an отрицательно. Другими словами, графики многочленов четных степеней при больших значениях переменной x похожи на график функции y = ax2. Если же n нечетно, то график
y = Qn(x) при больших x похож на график функции y = ax3; если an положительно, правая ветвь уйдет вверх, а левая — вниз, а если an отрицательно, то наоборот: правая — вниз, а левая — вверх.
3. Примеры.
Пример 1. График многочлена
Q3(x) = x3 + x2 – x – 1
можно построить сложением графиков функций y = x3, y = x2 и y = –x – 1. Поступим иначе. Разложим многочлен Q3(x) на множители:
x3 + x2 – x – 1 = (x3 + x2) – (x + 1) =
x2(x + 1) – (x + 1) = (x + 1)(x2 – 1) = (x + 1)2(x – 1).
Многочлен Q3(x) обращается в нуль при x = –1
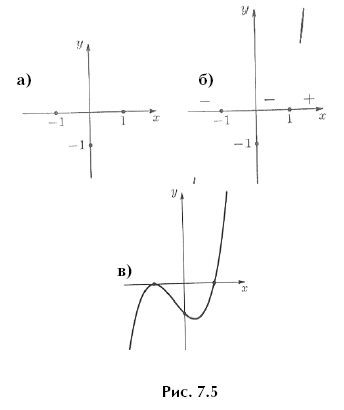
и при x = 1, значит, его график имеет с осью Ox две общие точки3. Понятно также, что график проходит через точку (0; –1) на оси Oy. Отметим эти три точки (рис. 7.5,а).
Знак многочлена (x + 1)2(x – 1) при заданном x определяется последним сомножителем: при
x > 1 многочлен Q3(x) положителен, а на промежутках –1 < x < 1 и x < –1 — отрицателен. Отметим это на рисунке 7.5,б.
Q3(x) — многочлен нечетной степени, значит, левая его ветвь уходит вниз, а правая — вверх. Отметим и это на чертеже (рис. 7.5,б) и будем проводить непрерывную плавную линию графика.
График идет снизу («от минус бесконечности») вверх направо до точки (–1; 0). В этой точке графику придется плавно повернуть вниз в точке
(0; –1) («плавно» потому, что «углов» на графиках многочленов не бывает). Значит, в точке (–1; 0)
график не пересекает оси Ox, а касается ее.
Далее график идет вниз, пересекает ось ординат в точке (0; –1) и, опустившись еще немного ниже, поворачивает, пересекает ось Ox в точке (1; 0) и круто уходит вверх.
Общий вид графика — на рисунке 7.5,в.
Пример 2. Чтобы построить график многочлена P(x) = x4 – 4x3 – 4x2 + 16x, мы разложим многочлен P(x) на множители. Для этого сначала вынесем за скобку x:
P(x) = x(x3 – 4x2 – 4x + 16).
Выражение в скобках разложим, используя группировку:
(x3 – 4x2) – (4x – 16) = x2(x – 4) – 4(x – 4) =
= (x – 4)(x2 – 4) = (x – 4)(x – 2)(x + 2).
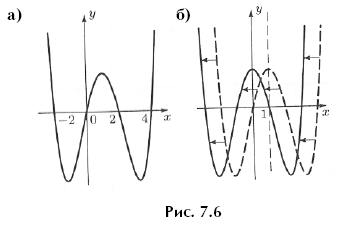
Теперь отметим на оси абсцисс нули функции P(x), то есть точки x = –2, x = 0, x = 2 и x = 4, и построим эскиз графика (рис. 7.6,а).
Замечание. Обратите внимание, что масштабы по осям координат на рисунке 7.6,а разные.
Полученный график не симметричен относительно оси Oy, так как функция P(x) не является четной. Однако на глаз представляется, что все-таки у этого графика есть ось симметрии, только не Oy, а прямая x = 1. Посмотрим, так ли это.
Сдвинем график y = P(x) на единицу влево, чтобы прямая x = 1 совместилась с осью Oy (см. рис. 7.6,б). Полученная кривая будет графиком функции y = P(x + 1). Чтобы получить формулу, задающую эту функцию, нужно в формулу для P(x) вместо x поставить x + 1. Воспользуемся представлением многочлена P(x) в виде произведения:
P(x) = (x + 2)x(x – 2)(x – 4).
Получим:
P(x + 1) = (x + 3)(x + 1)(x – 1)(x – 3) =
= (x2 – 9)(x2 – 1) = x4 – 10x2 + 9.
Мы видим, что многочлен P(x + 1) содержит только четные степени переменной x. Он является, тем самым, четной функцией, и его график симметричен относительно оси Oy.
Поэтому график P(x), получаемый из графика P(x + 1) сдвигом обратно, на единицу вправо, тоже будет симметричен, его осью симметрии будет прямая x = 1. Значит, наши глаза не обманули нас.
Многочлен x4 – 10x2 + 9 называется биквадратным трехчленом. Произвольный биквадратный трехчлен записывается в виде ax4 + bx2 + c. Нахождение его корней сводится, очевидно, к решению биквадратного уравнения az2 + bz + c = 0,
где z = x2.
Пример 3. Построим график многочлена
f(x) = x4 + x3 – 6x2 – x + 2.
Представим эту функцию в виде суммы двух многочленов:
f1(x) = x4 + x3 – 6x2 и f2(x) = –x + 2.
Многочлен x4 + x3 – 6x2 нетрудно разложить на множители. Вынесем за скобку x2, а выражение в скобках разложим, используя теорему Виета:
f1(x) = x2(x2 + x – 6) = x2(x + 3)(x – 2).
Теперь ясно, что график
f1(x) = x2(x + 3)(x – 2)
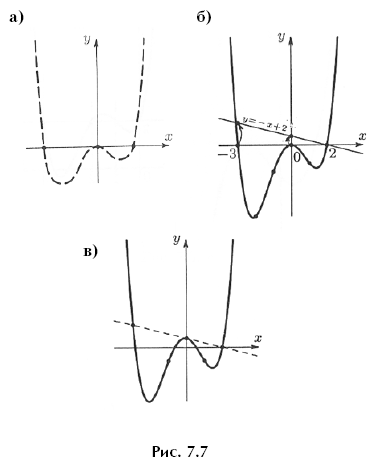
имеет с осью Ox три общие точки: x = –3, x = 0 и x = 2, причем при x = 0, где многочлен имеет двойной корень, график касается Ox, а на крайних интервалах, при x < –3 и при x > 2, ветви графика поднимаются вверх («к плюс бесконечности»). Отметим это на графике (рис. 7.7,а) и покажем схематически ход графика функции f1 штриховой линией.
Для уточнения вида графика найдем еще несколько значений функции
f1(x) = x2(x + 3)(x – 2):
например,
f1(–2) = –16, f1(–1) = –6, f1(1) = –4,
построим соответствующие точки и соединим их плавной кривой — рисунок 7.7,б. (Так как на участке от –2 ≤ x ≤ 2 значения функции, по сравнению с изменением аргумента, меняются довольно сильно, то на рисунке 7.7,б единица по оси Oy взята вчетверо меньшей, чем по оси Ox.)
Чтобы получить искомый график функции f(x) = x4 + x3 – 6x2 – x + 2, нужно график f1 «сложить» с графиком f2 (f2(x) = –x + 2). Тогда нули функции f1(x) «переедут» с оси Ox на прямую y = –x + 2. Полученная кривая при x = 0 будет касаться этой прямой. Общий вид графика — на рисунке 7.7,в.
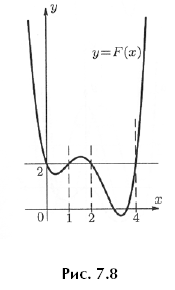
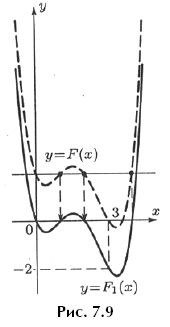
Пример 4. Решим теперь несколько необычную задачу. В предыдущих примерах были заданы разные многочлены и мы строили их графики. Теперь же на рисунке 7.8 задан график некоторого многочлена. Требуется угадать, что это за многочлен.
Заметим, прежде всего, что степень искомого многочлена четная: при больших по абсолютной величине значениях x он принимает значения одного знака. Поскольку эти значения положительные, старший коэффициент (при наибольшей степени x) тоже положителен.
Далее ясно, что степень многочлена больше двух: график совсем не похож на параболу.
Попробуем подобрать многочлен четвертой степени. Здесь был бы удобен прием, которым мы пользовались в примере 2 из этого параграфа: разложение многочлена на линейные множители. Однако искомый многочлен P(x), судя по графику, имеет только два нуля (то есть уравнение P(x) = 0 имеет только два корня, поэтому P(x) на линейные множители не разлагается
4.
Поступим так: проведем горизонтальную прямую так, чтобы она пересекла график в максимально большем числе точек. На рисунке 7.8 прямая y = 2 пересекает график в точках с абсциссами 0, 1, 2 и 4. Теперь заметим, что если опустить график на 2 единицы, то все четыре точки окажутся на оси Ox (рис. 7.9). Значит, многочлен P1(x) = P(x) – 2 можно искать в виде
P1(x) = ax(x – 1)(x – 2)(x – 4).
Чтобы найти a, возьмем какое-то значение x, при котором P1 не обращается в нуль. Например, x = 3. Получим: P1(3) = –6a. Судя по нарисованному графику, значение P(3) равно нулю и, значит, P1(3) = –2. Отсюда
и предполагаемый многочлен четвертой степени можно записать в виде:
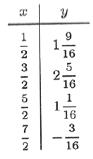
Чтобы проверить, дает ли эта формула разумное приближение для других точек графика, кроме уже использованных, нужны, конечно, дополнительные вычисления. Координаты нескольких таких контрольных точек, вычисленные по формуле (1), приведены в табличке. Все эти точки хорошо ложатся на заданный график, и найденную нами формулу можно считать вполне удовлетворительным ответом.
Упражнения
7-4. Постройте графики функций
y = x3 + 4x и y = x3 – 4x.
7-5. Постройте график многочлена y = x4 – 2x2 + 1 и график функции y = | x2 – 1 |. Сколько общих точек с осью Ox имеет каждый из этих графиков и какие именно? В чем различие этих двух графиков около этих точек?
Подсказка. Посмотрите п. 7 § 4.
7-6. Найдите точные координаты самых низких точек графика функции
y = x4 – 4x3 – 4x2 + 16x
(см. рис. 7.6,а). Указание. Используйте сдвиг по оси Ox (см. пример 3 выше) и замену u = x2.
7-7. По графику функции f(x) = x4 + x3 – 6x2 – x + 2
(рис. 7.6,в) видно, что многочлен x4 + x3 – 6x2 – x + 2
имеет четыре корня. Можно ли так изменить свободный член многочлена, чтобы уравнение
x4 + x3 – 6x2 – x + 2 = 0 имело три корня? два корня? один корень? не имело ни одного корня? имело 5 корней? В каждом случае утвердительного ответа нарисуйте эскиз графика.
7-8. Многочлен четвертой степени разложен на множители: Q4(x) = (x2 – 4x – 5)(x2 + px + q). Сколько корней может иметь уравнение (x2 – 4x – 5) ç
ç (x2 + px + q) = 0 в зависимости от значения параметров p и q? На каждый случай приведите пример и нарисуйте эскиз графика функции
y = Q4(x).
7-9. Докажите, что график многочлена
x4 + 4x3 + 5x2 + 2 имеет ось симметрии.
Подсказка. Сдвиньте график на единицу вправо.
7-10. Докажите, что график многочлена
y = x4 – 2x2 + 3x – 3 не имеет вертикальной оси симметрии.
7-11*. Найдите условие (или условия) того, что график многочлена четвертой степени
y = x4 + px3 + qx2 + rx + s имеет вертикальную ось симметрии.
7-12. Докажите, что никакая прямая y = kx + b
не может пересекать график многочлена четвертой степени более чем в четырех точках.
4. Симметрия графиков многочленов третьей степени. Вернемся к кубическим многочленам, с которыми мы уже встречались в предыдущем параграфе. Для графиков нечетных функций
y = ax3 и y = ax3 + bx начало координат является центром симметрии. Многочлены x3 + bx2 (при b, неравном нулю) не являются ни четными, ни нечетными. Но похоже, что их графики тоже имеют центр симметрии.
Мы теперь докажем, что этим свойством обладает график любого кубического многочлена.
В примере 3 пункта 3 мы решали похожую задачу про многочлен четвертой степени. Там заранее было понятно, что осью симметрии графика является прямая x = 1, и когда мы сдвинули график на единицу влево, в многочлене исчезли члены с x3 и x, «мешающие» функции быть четной.
Теперь мы не знаем, куда и насколько надо сдвинуть график функции y = x3 + px2 + qx + r, но нам ясна цель: надо «уничтожить» члены, мешающие нечетности, а именно, px2 и r. Со свободным членом r справиться легко, передвигая график параллельно оси Oy. Член px2 попробуем убрать, сдвигая график параллельно Ox.
Величину сдвига, которую мы не знаем, обозначим буквой h. Тогда уравнение сдвинутого графика получится заменой x на x – h:
f(x – h) = (x – h)3 + p(x – h)2 + q(x – h) + r.
Теперь надо подобрать число h, чтобы после раскрытия скобок член с x2 исчез. Начнем раскрывать скобки:
f(x – h) = (x – h)3 + p(x – h)2 + q(x
– h) + r
= x3 – 3hx2 + 3h2x – h3 + px2 + …
Дальше раскрывать скобки не обязательно, так как члена с x2 там не будет.
Итак, получаем:
f(x – h) = x3 – (3h – p)x2 + …
Теперь видно, что член с x2 исчезнет, если мы сдвинем график на
h=p/3. Тогда уравнение сдвинутой кривой примет вид: y = x3 + q1x + r1. Остается сдвинуть график на –r1 параллельно оси Oy, и мы получим нечетную функцию y = x3 + q1x, график которой симметричен относительно начала координат O(0; 0).
Мы доказали, что двумя сдвигами параллельно координатным осям график любого кубического многочлена можно сделать симметричным относительно начала координат
5. А так как при сдвигах форма графика не меняется, то получается следующий вывод.
Утверждение. График любого многочлена третьей степени имеет центр симметрии.
Так что, изучив формы графика функции
y = x3 + qx, мы узнаем, какой вид может иметь график кубического многочлена общего вида.
Мы уже строили графики y = x3 + qx для
q = 4 и q = –4 (см. упражнение 7-4) и получили две совершенно разные кривые. Могут ли быть еще какие-либо случаи?
Разложим многочлен x3 + qx на множители: x3 + qx = x(x2 + q). График y = x3 + qx проходит через начало координат — точку O(0; 0). Будут ли еще у графика точки, общие с осью Ox, зависит от того, будут ли корни, какие и сколько,
у уравнения x2 + q = 0.
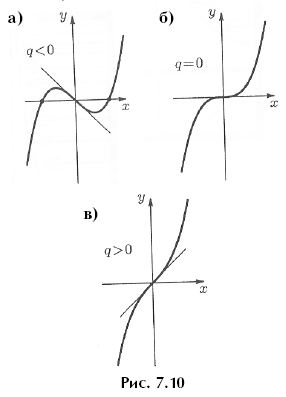
Возможны три случая: q < 0, q = 0 и q > 0.
В первом случае это уравнение имеет два корня:
и значит, график пересекает ось Ox еще в двух точках, симметричных относительно начала координат, и имеет вид, как на рисунке 7.10,а.
Во втором случае функция y = x3 + qx приобретает вид y = x3. График этой функции нам хорошо знаком — рисунок 7.10,б.
Наконец, если q > 0, то выражение x2 + q ни при каком значении x не может стать нулем. Значит, график y = x3 + qx пересекает ось Ox в единственной точке (в начале координат), функция монотонно растет и ее график выглядит, как на рисунке 7.10,в.
Упражнение
7-13. 1) Сдвиньте график y = x3 – 3x2 + 4x – 1
так, чтобы он стал симметричен относительно начала координат.
2) Найдите координаты центра симметрии графиков:
а) y = x3 – 3x2 + 4x – 1;
б) y = x3 + 3x2 + 2x – 2.
3) Какой вид имеют графики многочленов
y = x3 – 3x2 + 4x – 1 и y = x3 + 3x2 + 2x – 2?
1 Напоминаем, что степенью многочлена называется
наибольшая из степеней его членов.
2 Мы взяли в кавычки слова, точный смысл которых
определяется в курсах математического анализа. Здесь же нам будет достаточно
наглядных представлений.
3 Почему бы не сказать «график пересекает ось Ox
в двух точках»? Но, как вы сейчас увидите, такое утверждение было бы
неправильным.
4 Если бы P(x) был равен произведению (x – a)(x – b)(x – c)(x – d), то он имел бы четыре корня: a, b, c и d.
5 Другими словами, заменами x на x – h и y на y + r1 формулу, задающую функцию, можно привести к виду y = x3 + qx.
Гельфанд И., Глаголева Е. , Шноль Э.
График функции-многочлен
Содержание:
- График функции-многочлен
- Задача пример №12
- Задача пример №13
- Задача пример №14
График функции-многочлен
В стандартном виде функция — многочлен записывается как 
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 
Задача пример №12
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента но абсолютному значению.
Решение:
а) степень многочлена 




b) степень многочлена 




Задача пример №13
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
Отметим, что если n нечетно, то функция — многочлен имеет хотя бы один действительный нуль, если n четно, то их вообще может и не быть.
Алгоритм построения эскиза графика функции — многочлен:
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Задача пример №14
Постройте график функции 
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа 8: ±1; ±2; ±4; ±8 .
Проверим 


Зная, что 

Отсюда находим нули -1; 2; -4. Т.е. график пересекает ось абсцисс в точках (-4; 0), (-1; 0) и (2; 0). Так как 

2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 




3. Определим, как меняется график при уменьшении или увеличении значений 




4. Соединим отмеченные точки и получим схематический график функции 
Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Конус
- Ряды математика
- Вычислить длину дуги кривой
- Как найти ранг матрицы: пример решения
- Дробные рациональные выражения
- Знакочередующиеся ряды
- Производная неявной функции
- Неопределенный интеграл
- Формула Байеса
- Формулы приведения
3 способа расчета полинома в Excel.
Автор: Алексей Батурин.

- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН();
- 3-й способ с помощью Forecast4AC PRO;
Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.
Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).
Что такое полином? Полином — это степенная функция y=ax 2 +bx+c (полином второй степени) и y=ax 3 +bx 2 +cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.
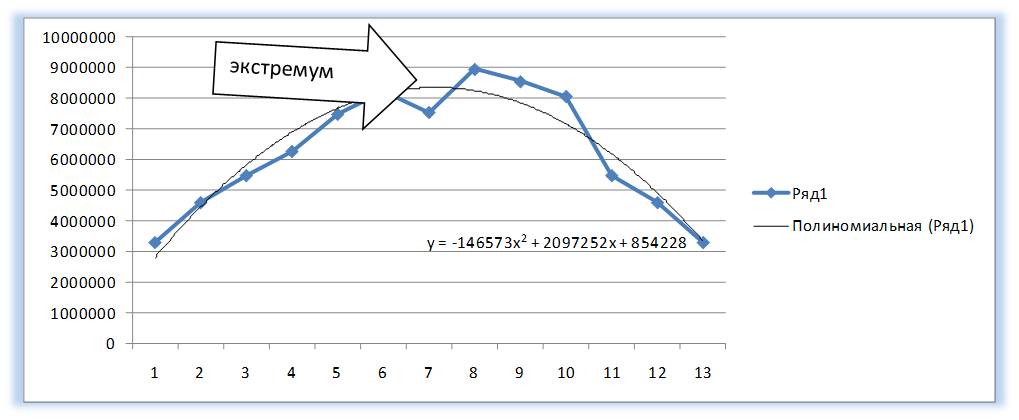
У полинома второй степени y=ax 2 +bx+c один экстремум (на графике ниже 1 максимум).
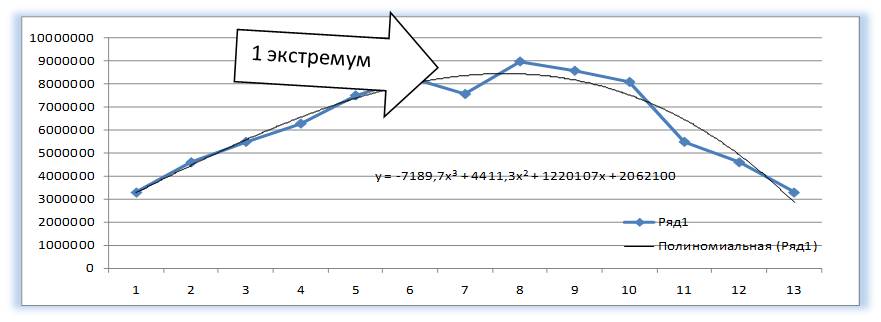
У Полинома третьей степени y=ax 3 +bx 2 +cx+d может быть один или два экстремума.
Один экстремум
Два экстремума
У Полинома четвертой степени не более трех экстремумов и т.д.
Как рассчитать значения полинома в Excel?
Есть 3 способа расчета значений полинома в Excel:
- 1-й способ с помощью графика;
- 2-й способ с помощью функции Excel =ЛИНЕЙН;
- 3-й способ с помощью Forecast4AC PRO;
1-й способ расчета полинома — с помощью графика
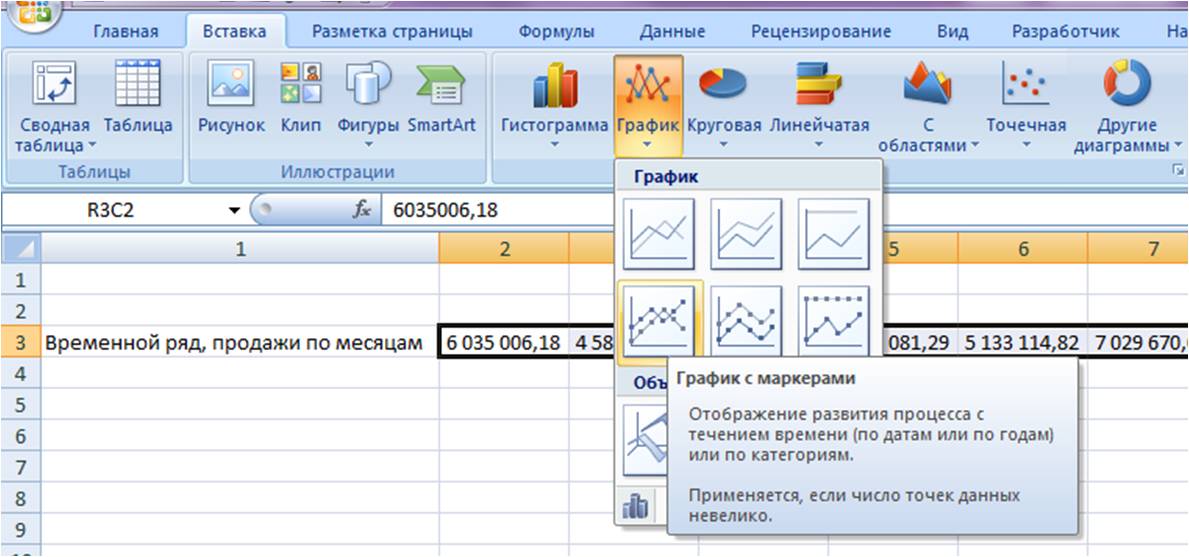
Выделяем ряд со значениями и строим график временного ряда.
На график добавляем полином 6-й степени.
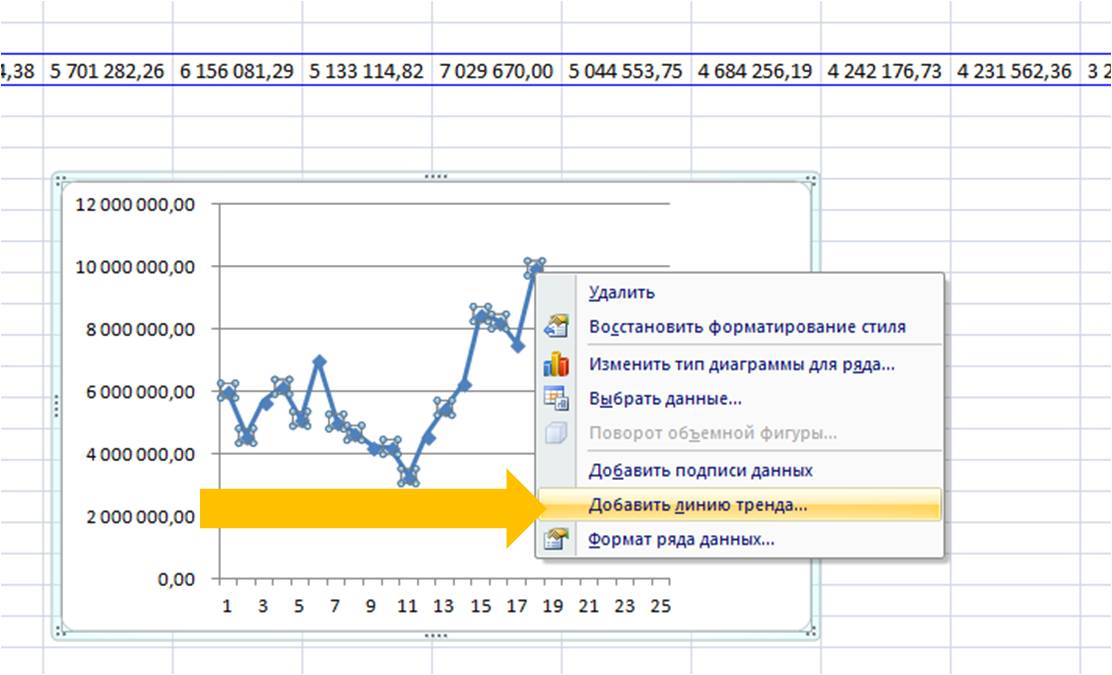
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»
После этого уравнение выводится на график y = 3,7066x 6 — 234,94x 5 + 4973,6x 4 — 35930x 3 — 7576,8x 2 + 645515x + 5E+06 . Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».
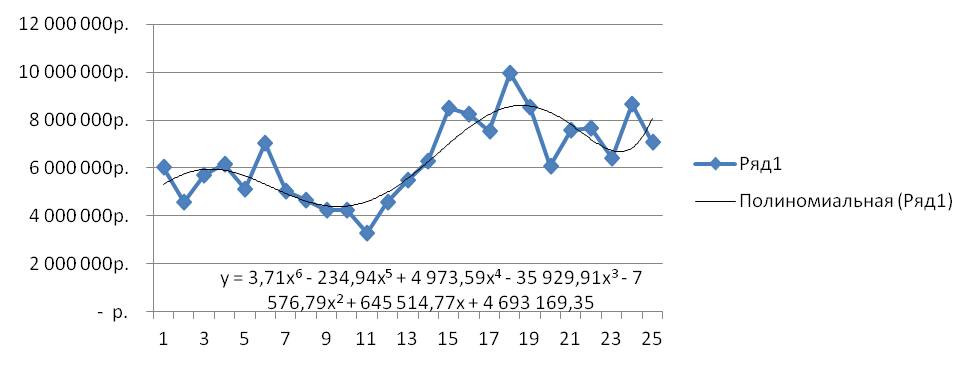
Получаем уравнение полинома в читаемом формате:
y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.
Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()
Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:
- «известные значения y» (объёмы продаж за периоды),
- «известные значения x» (порядковый номер временного ряда),
- в константу ставим «1»,
- в статистику «0»
Получаем следующего вида формулу:
Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.
Для этого в часть формулы с «известными значениями x» вписываем степень полинома:
- ^ <1:2:3:4:5:6>— для расчета коэффициентов полинома 6-й степени
- ^ <1:2:3:4:5>— для расчета коэффициентов полинома 5-й степени
- ^ <1:2>— для расчета коэффициентов полинома 2-й степени
Получаем формулу следующего вида:
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v
Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:
1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:
2. Нажать на клавишу F2
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)
Получаем 7 коэффициентов полиномиального тренда 6-й степени.
Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.
Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)
Получаем формулу следующего вида:
= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8
в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)
Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)
=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8
Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Устанавливаем курсор в начало временного ряда
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:
Копируем значения в наш лист.
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:
- Коэффициентов полиномиального тренда выведенных на график;
- Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
- и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Линия тренда в Excel на разных графиках
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Добавление линии тренда на график
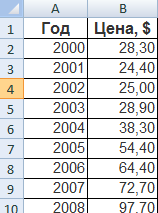
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
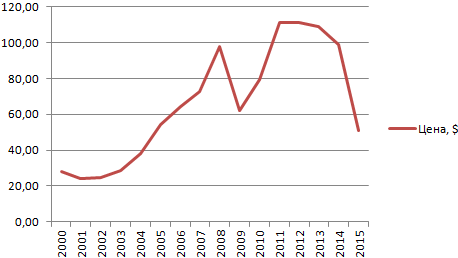
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
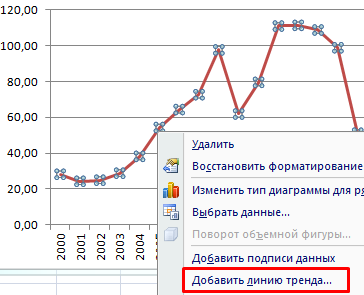
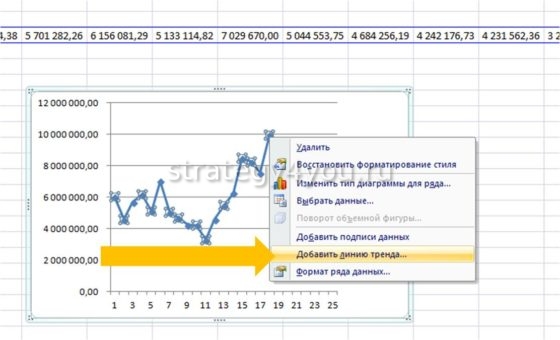
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
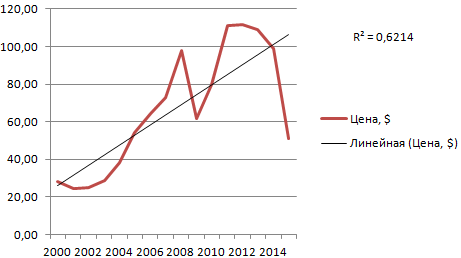
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
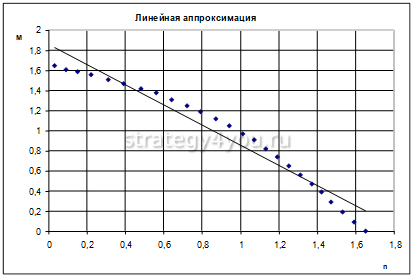
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
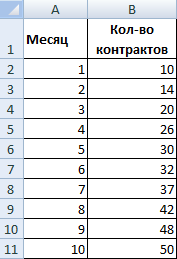
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
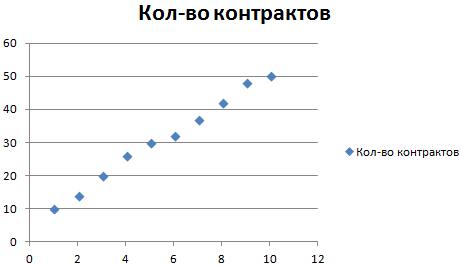
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
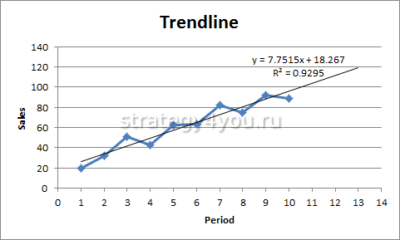
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
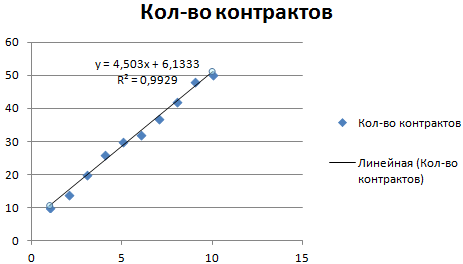
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
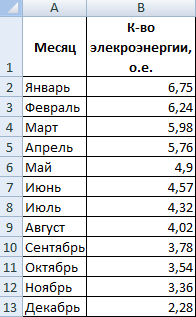
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
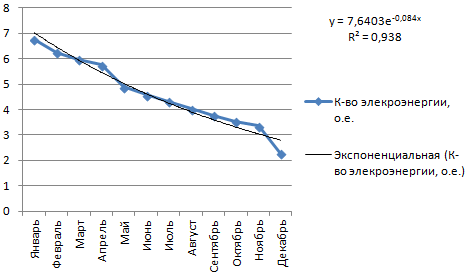
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
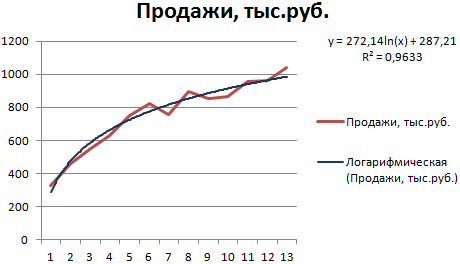
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
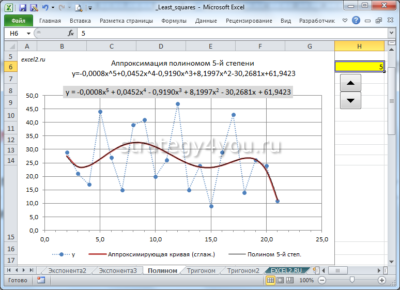
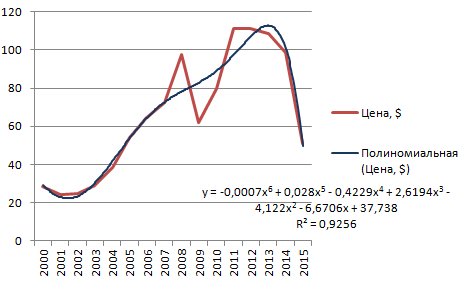
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Линия тренда в Excel (эксель): как построить, как добавить в диаграмму и что показывает, основные виды
Добавление трендовой линии на график
Данный элемент технического анализа позволяет визуально увидеть изменение цены за указанный период времени . Это может быть месяц, год или несколько лет. Информация будет отображать значение средних показателей в виде геометрических фигур. Добавить линию тренда в Excel 2010 можно с помощью встроенных стандартных инструментов.
Построение графика
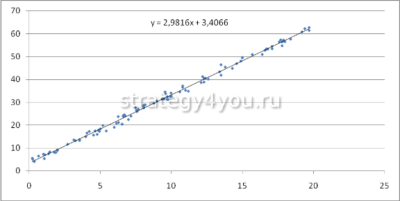
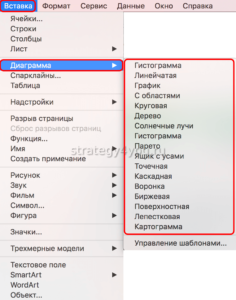
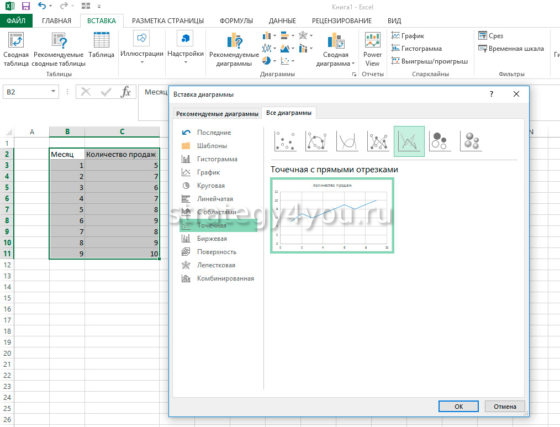
- Первым действием нужно выделить диапазон данных , например это А1:В9, затем активировать инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с гладкими кривыми и маркерами».
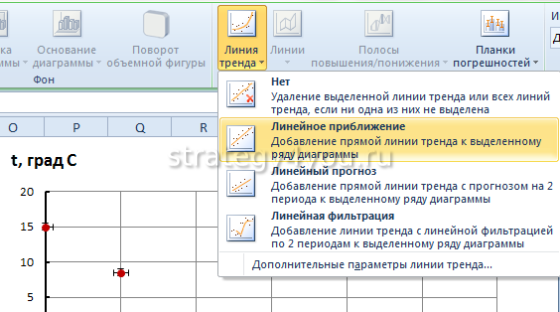
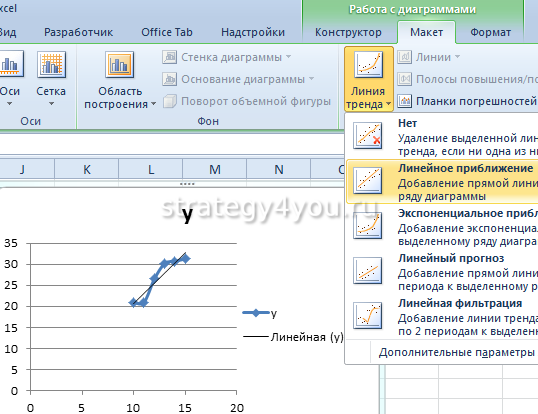
- После открытия графика пользователю станет доступна еще одна панель управления данными , на которой нужно выбрать следующее: «Работа с диаграммами»-«Макет»-«Линия тренда»-«Линейное приближение».
- Следующим шагом требуется выполнить двойной клик по образовавшейся линии тенденции в Excel . Когда появиться вспомогательное окно, отметить птичкой опцию «показывать уравнение на диаграмме».
Важно помнить, что если на графике имеется 2 или более линий , отображающих анализ данных, то перед выполнением 3 пункта нужно будет выбрать одну из них и включить в тенденцию. Эта короткая инструкция поможет начинающим специалистам разобраться, как строится линия тренда в Экселе.
Создание линии
Дальнейшая работа будет происходить непосредственно с трендовой линией.
Добавление тренда на диаграмму происходит следующим образом:
- Перейти во вкладку «Работа с диаграммами» , затем выбрать раздел «Макет»-«Анализ» и после подпункт «Линия тенденции» . Появится выпадающий список, в котором необходимо активировать строку «Линейное приближение».
- Если все выполнено правильно, в области построения диаграмм появится кривая линия черного цвета . По желанию цветовую гамму можно будет изменить на любую другую.
Этот способ поможет создать и построить тренд в Excel 2016 или более ранних версиях.
- лепесткового;
- кругового;
- поверхностного;
- кольцевого;
- объемного;
- с накоплением.
Настройка линии
Построение линий тренда имеет ряд вспомогательных настроек , которые помогут придать графику законченный и презентабельный вид.
Необходимо запомнить следующее:
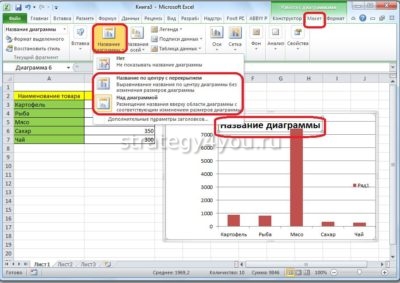
- Чтобы добавить название диаграмме , нужно дважды кликнуть по ней и в появившемся окне ввести заголовок. Для выбора расположения имени графика необходимо перейти во вкладку «Работа с диаграммами», затем выбрать «Макет» и «Название диаграммы». После этого появится список с возможным расположением заглавия.
- Дополнительно в этом же разделе можно найти пункт, отвечающий за названия осей и их расположение относительно графика. Интересно, что для вертикальной оси разработчики программы продумали возможность повернутого расположения наименования, чтобы диаграмма читалась удобно и выглядела гармонично.
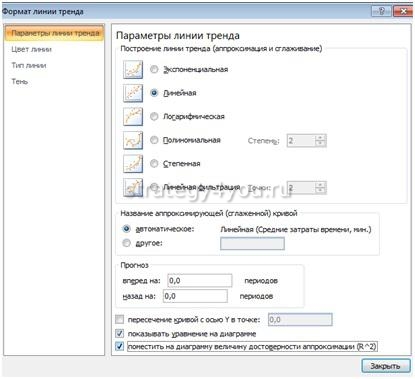
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
- Еще есть функция определения достоверности построенной модели . Для этого в дополнительных настройках требуется активировать пункт «Разместить на график величину достоверности аппроксимации» и после этого закрыть окно. Наилучшим значением является 1. Чем сильнее полученный показатель отличается от нее, тем ниже достоверность модели.
Прогнозирование
Для получения наиболее точного прогноза необходимо сменить построенный график на гистограмму . Это поможет сравнить уравнения.
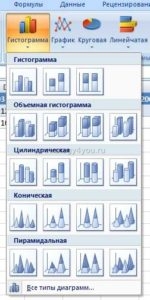
- Вызвать для графика контекстное меню и выбрать «Изменить тип диаграммы» .
- Появится новое окно с настройками , в котором требуется найти опцию «Гистограмма» и после выбрать подвид с группировкой.
Теперь пользователю должны быть видны оба графика . Они визуализируют одни и те же данные, но имеют разные уравнения для образования тенденции.
Следующим шагом необходимо сравнить уравнения точки пересечения с осями на разных диаграммах .
Для визуального отображения нужно сделать следующее:
- Перевести гистограмму в простой точечный график с гладкими кривыми и маркерами . Процесс выполняется через пункт контекстного меню «Изменить тип диаграммы…».
- Выполнить двойной клик по прямой образовавшейся тенденции , задать ей параметр прогноза назад на 12,0 и сохранить изменения.
Такая настройка поможет увидеть, что угол наклона тенденции меняется в зависимости от вида графика , но общее направление движения остается неизменным. Это свидетельствует о том, что построить линию тренда в Эксель можно лишь в качестве дополнительного инструмента анализа и брать его в расчет следует только как приближающий параметр. Строить аналитические прогнозы, основываясь лишь на этой прямой, не рекомендуется.
Уравнение линии тренда в Excel
Линейная аппроксимация
Введем в таблицу следующие данные:
Исходя из этих данных строится диаграмма , которая покажет рост заключенных сделок.
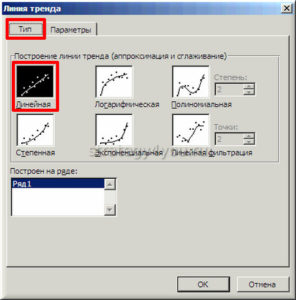
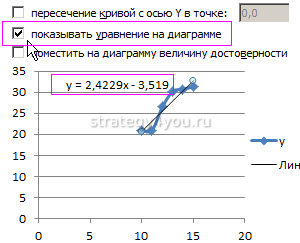
- Активировать график и добавить на него прямую тренда. В дополнительных настройках установить линейный вид.
- Добавить величину достоверности аппроксимации и уравнение тенденции . Такое построение использует уравнение: y = 4,503x + 6,1333, где 4,503 — показатель наклона, 6,1333 — смещения, y — последовательность значений, а х — номер периода. Формула размещает точки наиболее близко к прямой.
Прямая на диаграмме показывает стабильный рост работы сотрудника. Величина достоверности при этом равна 0,9929, что показывает наивысшую точность построения прогноза. Благодаря графику и уравнению можно просчитать количество сделок в будущем периоде . Для этого в формулу вместе х нужно подставить 11 (порядковый номер периода). По прогнозу в 11 месяце будет заключено 55-56 сделок.
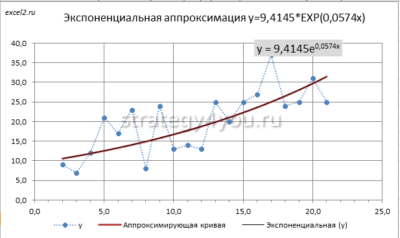
Экспоненциальная
Данный вид расчетов применяется в случае, когда вводимые данные меняются с непрерывно возрастающей скоростью . Экспоненциальное приближение не применяется, если присутствуют нулевые или отрицательные значения.
Логарифмическая
Для того чтобы узнать, как сделать грамотный расчет с определением линии тренда и как построить ее, нужна такая формула:
размер продаж = 272,14*LN(B18)+287,21 , где В18 соответствует порядковому номеру периода.
Полиномиальная
Данные формулы подскажут аналитикам, как правильно рассчитывать прямую тренда в различных ситуациях.
http://exceltable.com/grafiki/liniya-trenda-v-excel
17 авг. 2022 г.
читать 1 мин
Вы можете использовать функцию ЛИНЕЙН() в Excel, чтобы подобрать полиномиальную кривую с определенной степенью.
Например, вы можете использовать следующий базовый синтаксис, чтобы подогнать полиномиальную кривую со степенью 3:
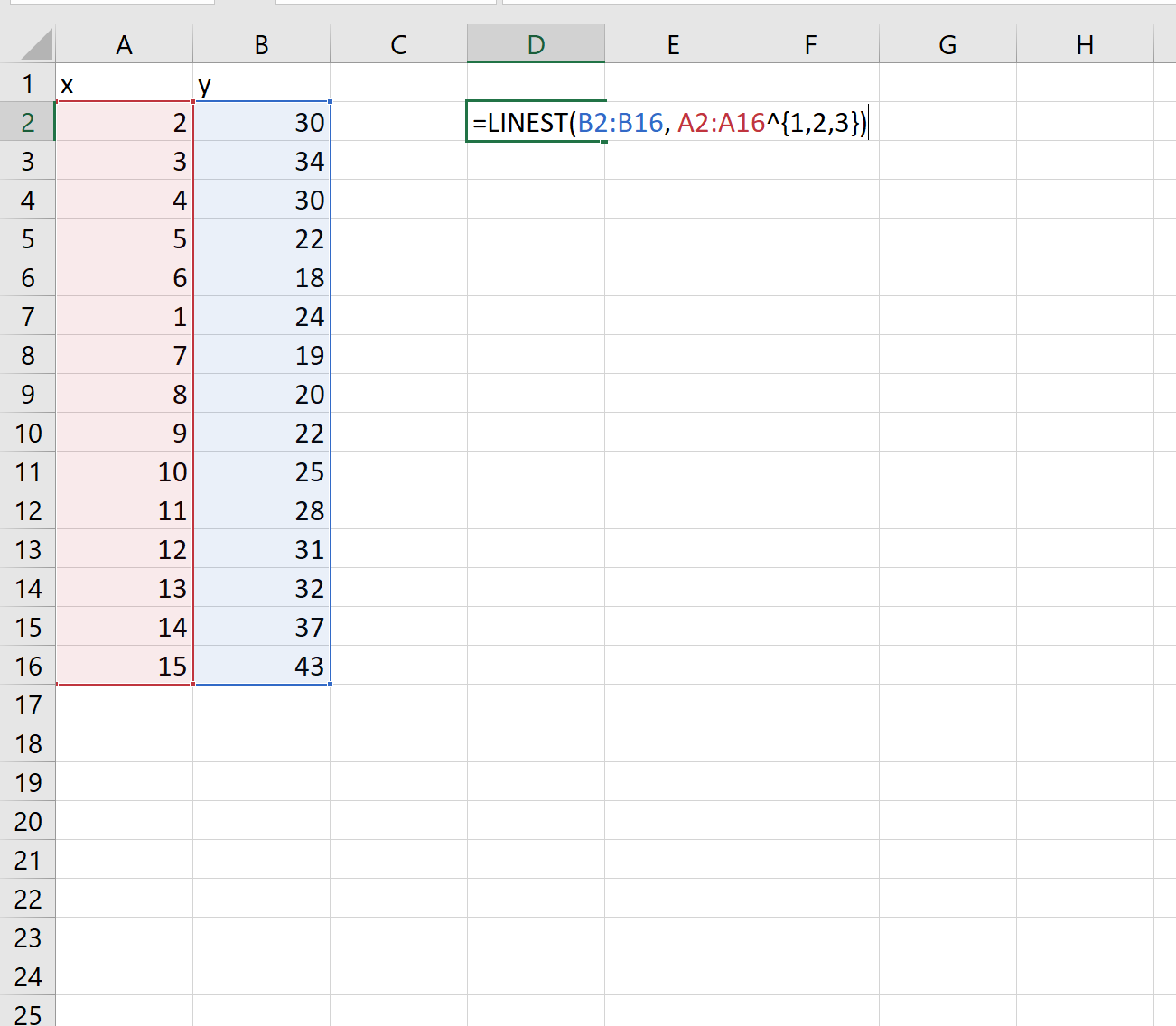
=LINEST( known_ys , known_xs ^{1, 2, 3})
Функция возвращает массив коэффициентов, описывающих полиномиальную подгонку.
В следующем пошаговом примере показано, как использовать эту функцию для подбора полиномиальной кривой в Excel.
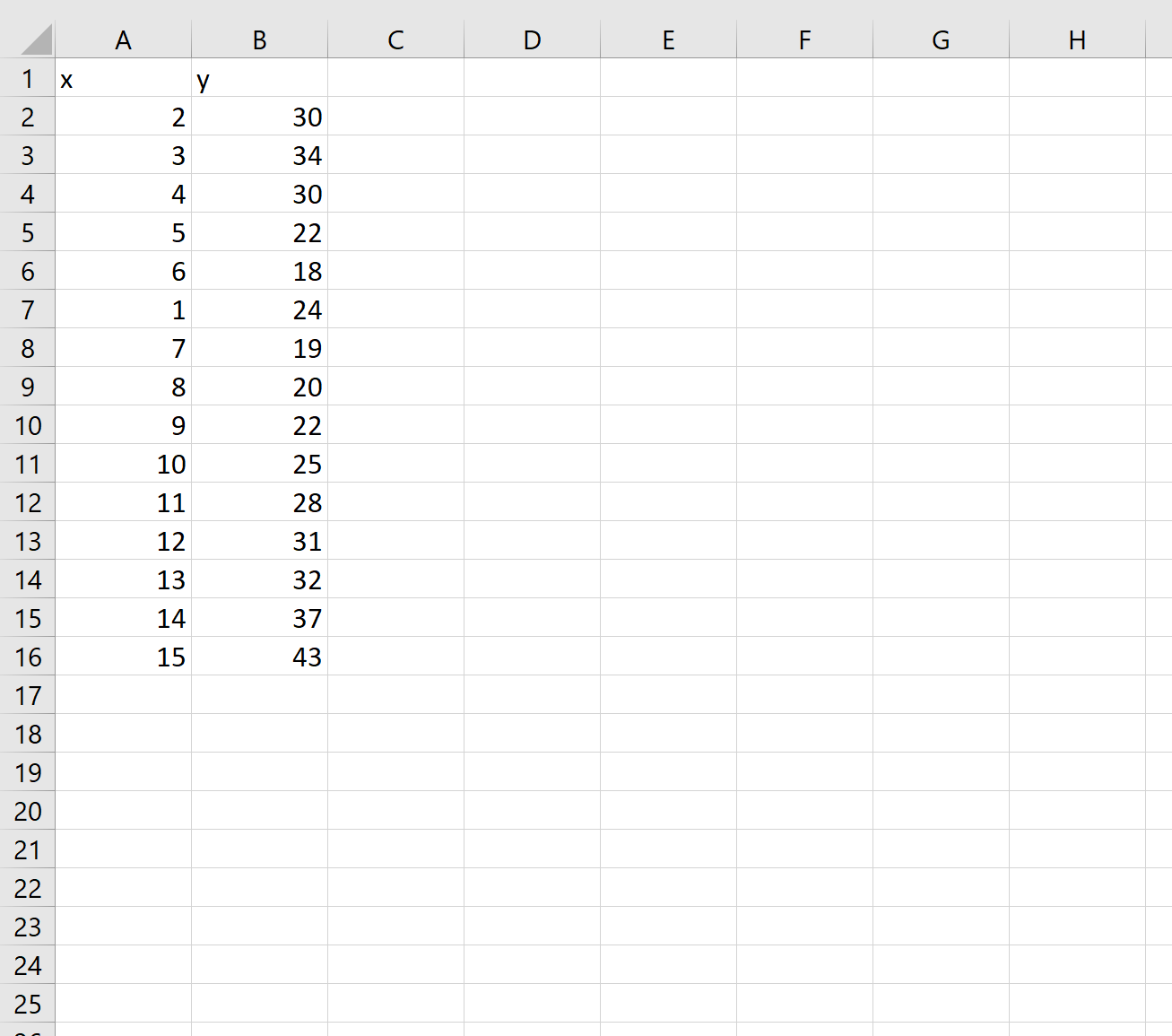
Шаг 1: Создайте данные
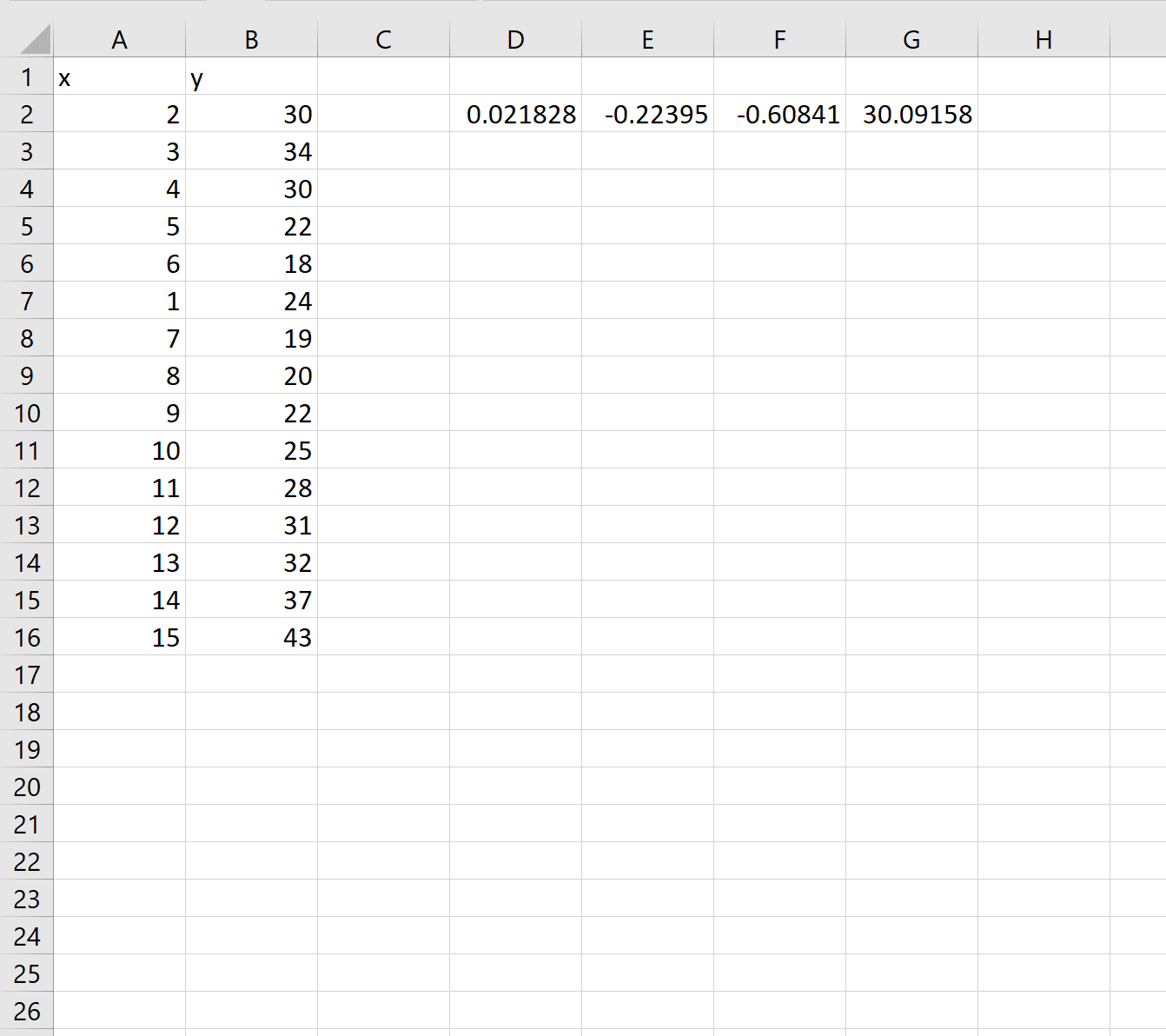
Во-первых, давайте создадим некоторые данные для работы:
Шаг 2: Подберите полиномиальную кривую
Далее воспользуемся функцией ЛИНЕЙН() , чтобы подобрать полиномиальную кривую степени 3 к набору данных:
Шаг 3: Интерпретация полиномиальной кривой
Как только мы нажмем ENTER , появится массив коэффициентов:
Используя эти коэффициенты, мы можем построить следующее уравнение, описывающее взаимосвязь между x и y:
у = 0,0218x 3 – 0,2239x 2 – 0,6084x + 30,0915
Мы также можем использовать это уравнение для вычисления ожидаемого значения y на основе значения x.
Например, предположим, что x = 4. Ожидаемое значение y будет следующим:
у = 0,0218(4) 3 – 0,2239(4) 2 – 0,6084(4) + 30,0915 = 25,47
Дополнительные ресурсы
Как выполнить полиномиальную регрессию в Excel
Как выполнить квадратичную регрессию в Excel
Как добавить квадратную линию тренда в Excel

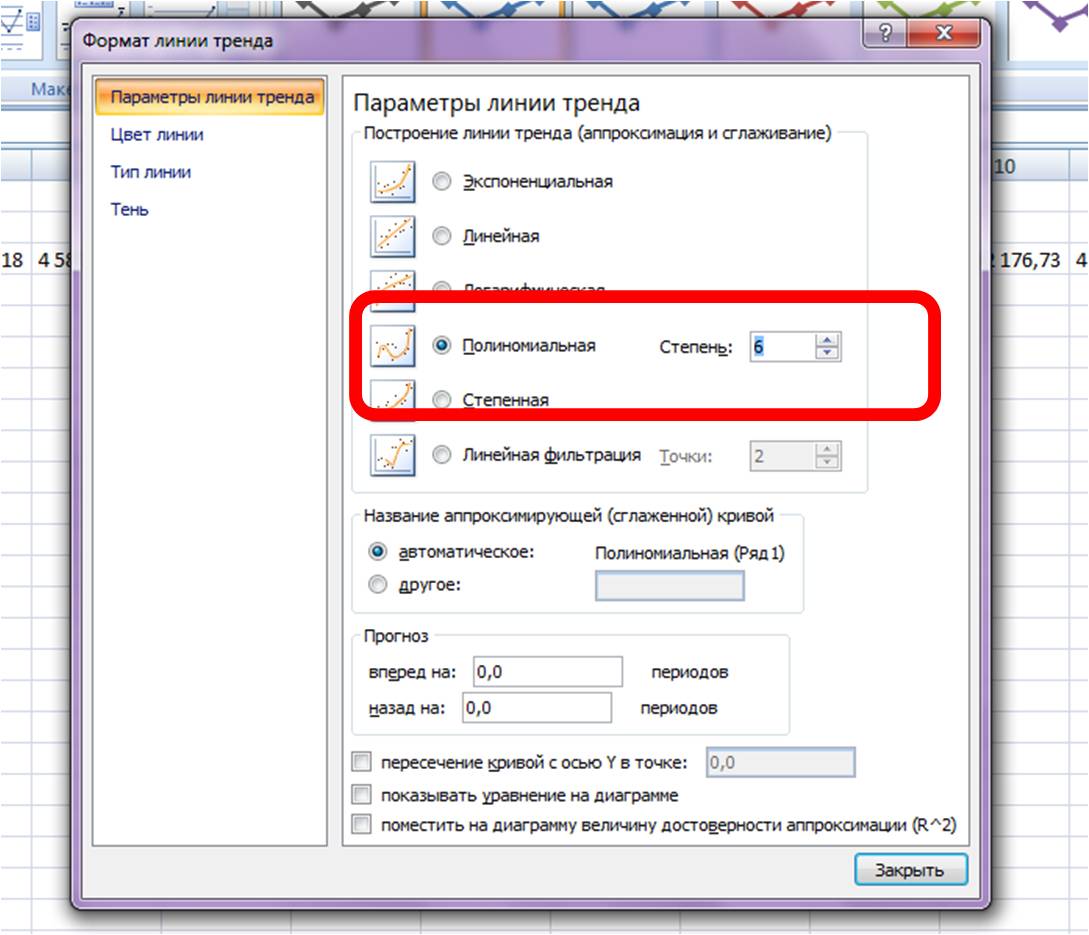





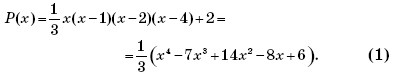






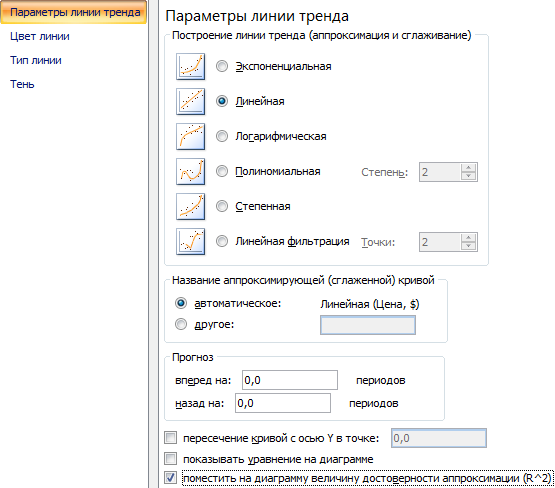

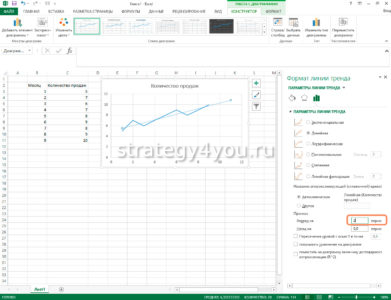 Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).
Чтобы внести изменения непосредственно в построение линий , нужно в разделе «Макет» найти «Анализ», затем «Прямая тренда» и в самом низу списка нажать «Дополнительные параметры…». Здесь можно изменить цвет и формат линии , выбрать один из параметров сглаживания и аппроксимации (степенный, полиноминальный, логарифмический и т.д.).