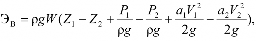Как найти мощность реки

Вода, двигаясь в
реках под действием сил тяжести, свершает
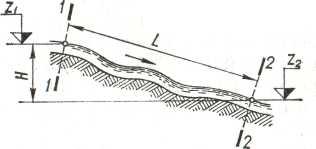
работу. Для двух сечений 1-1 и 2-2 реки на
участке длиной L,
согласно уравнению Д. Бернулли, удельная
энергия потока равна:

Е₁= z₁
+
+

Е₂= z₂
+
+

потенциальная
часть или энергия положения и давления
состоит:

z
– геометрическая высота (м),

— пьезометрическая
высота (м);

кинетическая часть
или скоростной напор —

(м).

где: γ = ρ*g
— объемный вес (кг/м³)

при этом плотность
воды ρ = 1000 (кг*с²/м⁴),
g
= 9,81 (м/с²)

α – коэффициент
кинетической энергии потока (коэффициент
Кориолиса), учитывающий неравномерность
распределения скоростей по сечению.
Для равномерного турбулентного потока
по экспериментальным данным α = 1,03 –
1,1

Разность
удельных энергий потока в сечениях
1—1 и 2—2
представляет
собой работу
(срабатываемый напор Н),
которую совершает
1 кг
воды
при его перемещении
из первого сечения во второе:

Рисунок 1. Схема к
определению работы речного потока.

Н
= (z₁
+
+
)
– (z₂
+
+
),
м.

Предполагая,
что давления и
кинетические энергии потока в
рассматриваемых сечениях равны, поэтому
работу, совершаемую весовым расходом
ρgQ
в
единицу
времени, определяют по формуле:

N
= ρgQ(z₁
– z₂)
= ρgQH,
Вт.

Величина
расхода равна произведению скорости
потока и площади сечения: Q
= v*s,
м³/с.

Подставляя
γ = ρ*g
= 1000*9,81 (кг/м³)
и выражая мощность в кВт, получим:

Nпотока
=
= 9,81QH,
кВт.

Эта
мощность речного потока в естественном
состоянии расходуется на преодоление
сил трения о ложе реки, взаимное гашение
энергии потока и т.д. Для использования
энергии данного участка реки в целях
получения электроэнергии, необходимо
искусственно сконцентрировать падение
этого участка в одном каком-либо месте,
т.е. создать разность уровней воды,
которую называют статическим
напором.

Путем
строительства на реках гидроэлектростанций
и установкой
в здании ГЭС гидроагрегатов гидравлическая
энергия потока, рассредоточенная
на определенном участке реки,
концентрируется в
одном месте и преобразуется в электрическую.

1.3.3 Схемы и компоновка гидроузлов.

Рисунок.
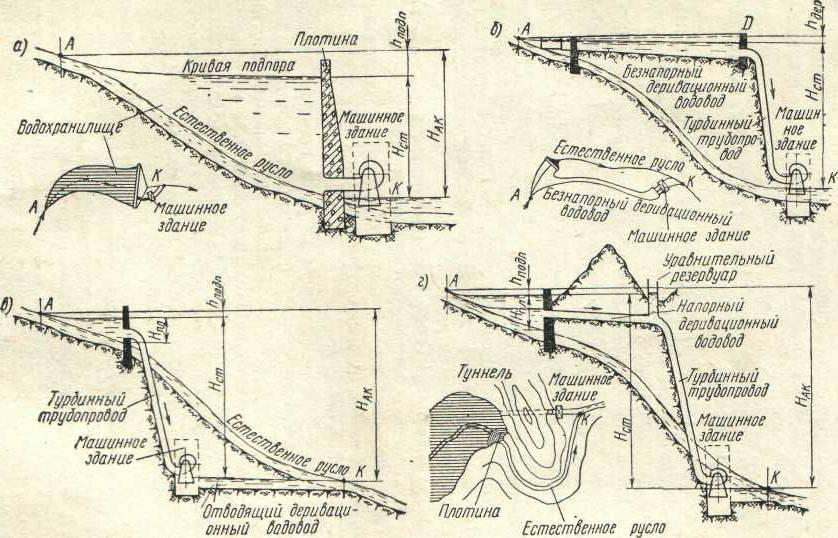
2. Схемы создания напора в приплотинных
и деривационных ГЭС.

В
практике гидроэнергетического
строительства применяют различные
технические схемы использования водной
энергии.
В зависимости от местных условий,
концентрация напора на ГЭС достигается
при помощи гидротехнических сооружений,
образующих
следующие технические схемы: плотинную,
деривационную и
плотинно-деривационную.

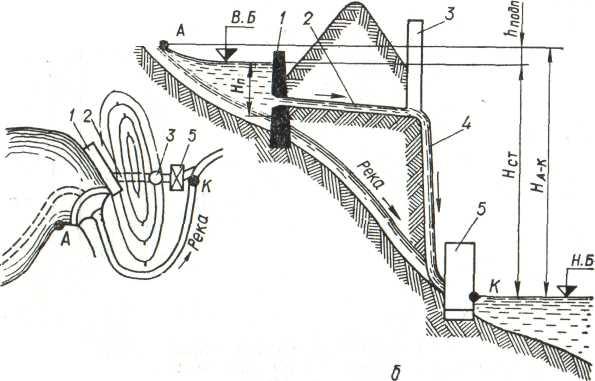
Плотинная
схема
(рис. 2а). Эта схема характеризуется
наличием плотины, которая создает
разность отметок уровней перед плотиной
(верхний бьеф) и за плотиной (нижний
бьеф). Поверхность воды в верхнем
бьефе перед плотиной в разрезе вдоль
потока образует так называемую кривую
подпора. Вследствие этого используемый
статический напор Н_ст
получается несколько меньше разности
отметок подпертого участка реки Н_ак
между пунктами А и К на величину
h_подп.

В
плотинных схемах гидроузлов здание
машинного зала располагается рядом с
плотиной или в плотине, при этом в
зависимости от величины напора и размеров
гидротурбин гидростанции могут быть
двух типов — русловые
и приплотинные.

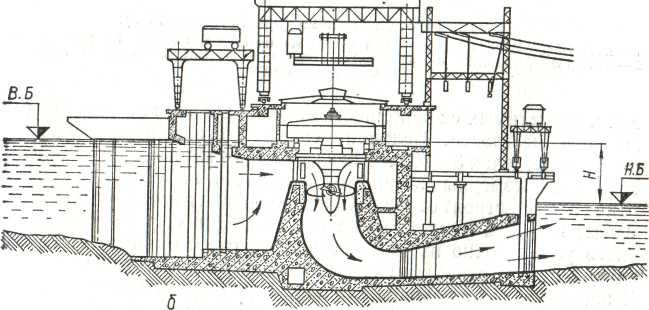
Русловые
— здание
ГЭС входит в состав сооружений, создающих
напор (рис.3), и полностью воспринимает
сдвигающие и опрокидывающие усилия,
действующие на него со стороны воды.
ГЭС такого типа строят при напорах 3 —
40 м и устанавливают на них, главным
образом, осевые гидротурбины.

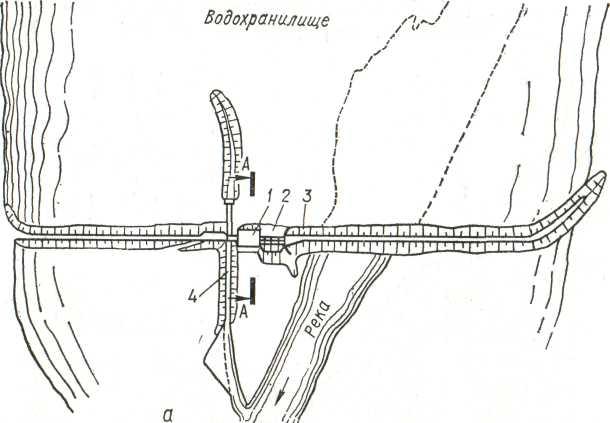
Рисунок
3. Плотинная схема. Русловая ГЭС.

а –
план сооружений, б – поперечный разрез
по зданию. 1 – здание ГЭС. 2 – водосливная
плотина. 3 – земляная плотина. 4 – шлюз.

Приплотинные
— здание ГЭС находится непосредственно
за плотиной (рис. 4а).
Такие ГЭС строят при средних и высоких
напорах (Н = 40 – 300 м). Подвод воды к
турбинам осуществляется при помощи
водоприемников и турбинных водоводов.
Устанавливаемые типы турбин: осевые
или диагональные поворотно-лопастные
и радиально-осевые, в зависимости от
величины напора, графика нагрузки и
требований, предъявляемых к установке
турбин на ГЭС.

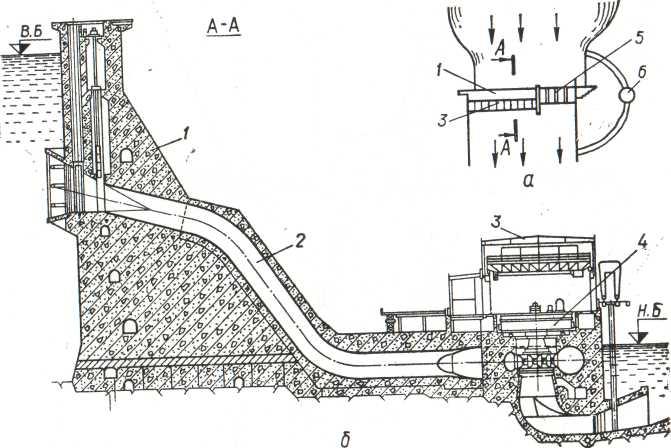
Рисунок 4. Плотинная схема. Приплотинная
ГЭС.

а – план сооружений; б — поперечный
разрез по плотине и зданию.

1 — плотина глухая; 2 – водоводы; 3 —
здание ГЭС; 4 — гидроагрегат; 5 —
плотина водосливная; 6 — судоподъемник.

Пример русловой
станции – Майнская ГЭС, приплотинной
– Саяно-Шушенская ГЭС.

Напор,
создаваемый плотиной, обычно небольшой,
но он может доходить до 230 м; например,
на Нурекской ГЭС на реке Вахш высота
плотины около 300 м. (Саяно-Шушенская ГЭС:
Н_пл
= 242 м, Н_расч=194
м) Высота плотины и создаваемый ею напор
определяются топографическими условиями
местности, расположенной выше плотины,
и допустимыми пространствами
затопления.

Деривационная
схема (рис
2б,
2в).
При больших уклонах рек с относительно
малыми расходами воду отводят в так
называемую деривацию (канал или
туннель). Гидравлический уклон деривации
выбирают минимальным, обеспечивающим
необходимый расход. Таким образом,
значительный перепад реки, в естественном
состоянии рассредоточенный на большом
протяжении, при помощи деривации
концентрируют в одном месте, где
строят здание ГЭС и устанавливают
гидроагрегаты. Трасса деривации
должна быть по возможности кратчайшей,
чтобы избежать дополнительных потерь
напора. Деривация может быть подводящей
(рис 2б) или отводящей (рис. 2в). Одна из
возможных схем указана на рис. 5.

Р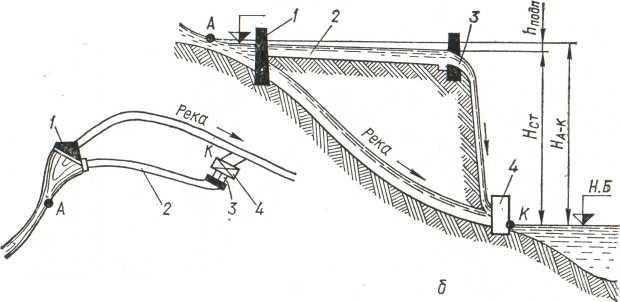ис.
5. Деривационная схема:

а —
план сооружений; б — вертикальный
разрез: / — плотина; 2
—
деривация; 3 — турбинные
водоводы;
4
— здание
ГЭС.

Напоры,
создаваемые при помощи деривации,
находятся в пределах Н = 200 – 2000 м и
зависят от природных и других условий.
На деривационных ГЭС применяют следующие
типы турбин: радиально-осевые (Н < 650
м) или ковшовые (Н > 300 м).

Плотинно-деривационная
схема
(рис. 4г). Напор на станции создается
при помощи плотины и деривации
одновременно. Если река на верхнем
участке имеет малый уклон, там целесообразно
построить плотину и создать
водохранилище, которое будет использовано
для регулирования расхода на ГЭС.
Основная часть напора создается, как
правило, деривацией. Величина напоров
и используемое турбинное оборудование
такие же, как и в случае деривационной
схемы.

Рис. 5.
Плотинно-деривационная схема:

а
— план сооружений; 6 — вертикальный
разрез: 1 — плотина; 2 — деривация; 3 —
уравнительный резервуар; 4 — турбинные
водоводы; 5 — здание ГЭС.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Главнейшей особенностью гидроэлектростанций, отличающей их от других источников энергии, является использование ими естественно возобновляемых гидроэнергетических ресурсов.

О мощи водной энергии древнекитайский философ Лао-цзы (IV–III вв. до н.э.) писал: «хотя в мире нет предмета, который был бы слабее и нежнее воды, но она может разрушить самый твердый предмет».

Водная энергия (гидроэнергия) – механическая энергия воды водотока (например реки) с продольным уклоном (падением), по которому вода движется под действием собственной массы, а также потенциальная энергия воды в искусственных (водохранилища) или естественных (озера) водоемах, расположенных на определенной высоте над уровнем моря.

Развитие гидроэнергетики на всех этапах характеризуется неуклонным увеличением мощностей строящихся ГЭС и повышением эффективности использования местных гидроэнергетических ресурсов. За период чуть более 100 лет мощность ГЭС возросла в сотни раз. Сегодня мощность крупнейших в мире ГЭС Итайпу на р. Парана (Бразилия–Парагвай) составляет 12600 МВт, а ГЭС «Три ущелья» на р. Янцзы (Китай) – 18200 МВт.

Ниагарский водопад

Огромную силу Ниагарского водопада долго рассматривали как источник энергии.

Ниагарский водопад – общее название трех водопадов (справа – «Подкова», иногда называемый Канадским водопадом, слева – Американский водопад и водопад «Фата») на реке Ниагара – мощнейший в Северной Америке. Высота водопадов составляет 53 м, а объем падающей воды достигает 5720 м 3 /с. Наиболее мощными гидроэлектростанциями на реке Ниагара являются «Сэр Адам Бек 1» и «Сэр Адам Бек 2», находящиеся на канадской стороне, а также гидроэлектростанция Роберт Мозес (Robert Moses) и насосная станция «Левистон» (Lewiston Pump Generating Plant) на американской стороне. Их совокупная мощность составляет 4,4 ГВт.

ГЭС вырабатывает электроэнергию в результате преобразования энергии водного потока. Реки, спускаясь с гор и возвышенностей к морям и озерам, обладают постоянно возобновляемой природой энергией. В естественных условиях эта энергия тратится на преодоление сил трения при взаимодействии потока с руслом, на преодоление порогов и других препятствий, перемещение наносов.

Энергию водотока за время t на выделен ном участке реки между сечениями 1-1 и 2-2 (рис. 2.1) можно определить как разность энергии потока в этих сечениях на основании уравнения Бернулли:

где Эв – энергия водотока на выделенном участке, Дж; t – время, с; g – 9,81 – ускорение свободного падения м/с2; ρ – плотность жидкости, кг/м3 (для водотоков с чистой пресной водой ρ=1000 кг/м3); W – объем стока воды, м3; Z1 и Z2 – геометрическая высота над плоскостью сравнения в сечениях 1-1 и 2-2, м; P 1 и P 2 – давление в сечениях 1-1 и 2-2, Па; V 1 и V 2 – средняя скорость воды в сечениях 1-1 и 2-2, м/с; a – коэффициент кинетической энергии (Кориолиса).

Учитывая, что в естественных условиях разность кинетической энергии в сечениях 1-1 и 2-2 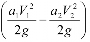крайне незначительна, ею можно пренебречь. Тогда для водотоков с чистой пресной водой энергию и мощность водотока можно определить по формулам

Э в = 9,81 WH в;

Э в = N в t ;

N в = 9,81 QH в,

где напор на выделенном участке H в = Z 1 – Z 2 равен разности уровней (падению уровня) свободной поверхности водотока на выделенном участке реки; Q – средний расход реки на выделенном участке, м 3 /с; N в – средняя мощность водотока за время t на выделенном участке, кВт.

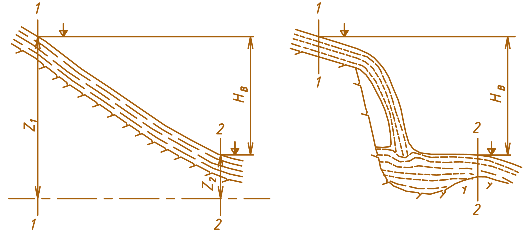
Рис. 2.1. Схемы естественных водоемов

На некоторых реках самой природой созданы сосредоточенные перепады уровней – водопады. В ряде случаев они использовались для создания напора ГЭС.

Водопады Игуасу, Южная Америка

На ГЭС можно использовать также перепад между уровнями воды двух смежных рек в местах их сравнительно небольшого удаления.

Энергия реки на ГЭС преобразовывается в электроэнергию при создании на выделенном участке реки сосредоточенного перепада (напора).

Для получения электроэнергии также может использоваться энергия приливно-отливных колебаний морей и океанов, энергия волн, потоков с высокими скоростями течения.

Водопад Виктория, Африка

Источник

Движущаяся вода обладает киненетической энергией, следовательно можно получать из неё эту энергию и преобразовывать в электричество. (если надо вывод формулы даже могу сделать ) Итак: сначала посчитаем площадь сечения ручья 0,2м*1м= 0,2 м^2. Зависимость мощности от скорости кубическая. Далее: плотность воды ((1000 кг/м^3)* скорость (0,4м/с)^3)/2 = 32. И это 32 умножаем на площадь сечения, результат получается в киловаттах: 32*0,2 = 6,4кВт. Это мощность всего потока воды.

Можно соорудить довольно большую тихоходную нижнебойную турбинку, либо можно сделать плотинку, но не для поднятия уровня, а для «сужения» потока, тогда его скороть выростет, и турбина будет менее громоздкая и требовательная к размещению.

По умолчанию что то вот такое надо: http://www.rosinmn.ru/gidro/gidro_index.html

Изменено 03.12.2011 17:36 пользователем Denison

Источник

From Wikipedia, the free encyclopedia

Stream power
Water flowing in creek
Common symbols	Ω, ω
SI unit	Watts
In SI base units	kg m² s⁻³
Derivations from other quantities	Ω=ρgQS
Dimension	M L² T⁻³

Stream power, originally derived by R. A. Bagnold in the 1960s, is the amount of energy the water in a river or stream is exerting on the sides and bottom of the river.^[1] Stream power is the result of multiplying the density of the water, the acceleration of the water due to gravity, the volume of water flowing through the river, and the slope of that water. There are many forms of the stream power formula with varying utilities, such as comparing rivers of various widths or quantifying the energy required to move sediment of a certain size. Stream power is closely related to other criteria such as stream competency and shear stress. Stream power is a valuable measurement for hydrologists and geomorphologists tackling sediment transport issues as well as for civil engineers, who use it in the planning and construction of roads, bridges, dams, and culverts.

History[edit]

Although many authors had suggested the use of power formulas in sediment transport in the decades preceding Bagnold’s work,^[2]^[3] and in fact Bagnold himself suggested it a decade before putting it into practice in one of his other works,^[4] it wasn’t until 1966 that R. A. Bagnold tested this theory experimentally to validate whether it would indeed work or not.^[1] This was successful and since then, many variations and applications of stream power have surfaced. The lack of fixed guidelines on how to define stream power in this early stage lead to many authors publishing work under the name «stream power» while not always measuring the entity in the same way; this led to partially failed efforts to establish naming conventions for the various forms of the formula by Rhoads two decades later in 1986.^[5]^[6] Today stream power is still used and new ways of applying it are still being discovered and researched, with a large integration into modern numerical models utilizing computer simulations.^[5]^[7]^[8]^[9]

Derivation[edit]

It can be derived by the fact that if the water is not accelerating and the river cross-section stays constant (generally good assumptions for an averaged reach of a stream over a modest distance), all of the potential energy lost as the water flows downstream must be used up in friction or work against the bed: none can be added to kinetic energy. Therefore, the potential energy drop is equal to the work done to the bed and banks, which is the stream power.

We know that change in potential energy over change in time is given by the equation:

${frac {Delta PE}{Delta t}}=mg{frac {Delta z}{Delta t}}$

where water mass and gravitational acceleration are constant. We can use the channel slope and the stream velocity as a stand-in for : the water will lose elevation at a rate given by the downward component of velocity $u_{z}$ . For a channel slope (as measured from the horizontal) of alpha :

${frac {Delta z}{Delta t}}=u_{z}=usin(alpha )approx uS$

where is the downstream flow velocity. It is noted that for small angles, . Rewriting the first equation, we now have:

${frac {Delta PE}{Delta t}}=mguS$

Remembering that power is energy per time and using the equivalence between work against the bed and loss in potential energy, we can write:

$Omega ={frac {Delta PE}{Delta t}}$

Finally, we know that mass is equal to density times volume. From this, we can rewrite the mass on the right hand side

where is the channel length, is the channel width (breadth), and is the channel depth (height). We use the definition of discharge

where is the cross-sectional area, which can often be reasonably approximated as a rectangle with the characteristic width and depth. This absorbs velocity, width, and depth. We define stream power per unit channel length, so that term goes to 1, and the derivation is complete.

Various Forms[edit]

(Total) Stream power[edit]

Stream power is the rate of energy dissipation against the bed and banks of a river or stream per unit downstream length. It is given by the equation:

where Ω is the stream power, ρ is the density of water (1000 kg/m³), g is acceleration due to gravity (9.8 m/s²), Q is discharge (m³/s), and S is the channel slope.^[5]

Total Stream Power[edit]

Total stream power often refers simply to stream power, but some authors use it as the rate of energy dissipation against the bed and banks of a river or stream per entire stream length. It is given by the equation:

where Ω is the stream power, per unit downstream length and L is the length of the stream.^[7]^[5]

Unit (or Specific) Stream power[edit]

Unit stream power is stream power per unit channel width, and is given by the equation:

$omega ={frac {rho gQS}{b}}$

where ω is the unit stream power, and b is the width of the channel. Normalizing the stream power by the width of the river allows for a better comparison between rivers of various widths.^[5] This also provides a better estimation of the sediment carrying capacity of the river as wide rivers with high stream power are exerting less force per surface area than a narrow river with the same stream power, as they are losing the same amount of energy but in the narrow river it is concentrated into a smaller area.

Critical Unit Stream Power[edit]

Critical unit stream power is the amount of stream power needed to displace a grain of a specific size, it is given by the equation:

${displaystyle omega _{0}=tau _{0}nu _{0}}$

where τ₀ is the critical shear stress of the grain size that will be moved which can be found in the literature or experimentally determined while v₀ is the critical mobilization speed.^[10]^[11]

Relationships to other variables[edit]

Size of displaced sediment[edit]

Critical stream power can be used to determine the stream competency of a river, which is a measure to determine the largest grain size that will be moved by a river. In rivers with large sediment sizes the relationship between critical unit stream power and sediment diameter displaced can be reduced to:^[12]^[13]

${displaystyle omega _{0}=0.030D_{i}^{1.69}}$

While in intermediate-sized rivers the relationship was found to follow:^[12]

${displaystyle omega _{0}=0.130D_{i}^{1.438}}$

Shear stress[edit]

Shear stress is another variable used in erosion and sediment transport models representing the force applied on a surface by a perpendicular force, and can be calculated using the following formula

Where τ is the shear stress, S is the slope of the water, ρ is the density of water (1000 kg/m³), g is acceleration due to gravity (9.8 m/s²).^[14]
Shear stress can be used to compute the unit stream power using the formula

Where V is the velocity of the water in the stream.^[14]

Applications[edit]

Landscape evolution[edit]

An example of a map displaying a stream power index (SPI) alongside an index displaying how wet the ground is (TWI)

Stream power is used extensively in models of landscape evolution and river incision. Unit stream power is often used for this, because simple models use and evolve a 1-dimensional downstream profile of the river channel. It is also used with relation to river channel migration, and in some cases is applied to sediment transport.^[1]

Predicting flood plain formation[edit]

By plotting stream power along the length of a river course as a second-order exponential curve, you are able to identify areas where flood plains may form and why they will form there.^[15]

Sensitivity to erosion[edit]

Stream power has also been used as a criterion to determine whether a river is in a state of reshaping itself or whether it is stable. A value of unit stream power between 30 and 35 W m⁻² in which this transition occurs has been found by multiple studies.^[7]^[16]^[17] Another technique gaining popularity is using a gradient of stream power by comparing the unit stream power upstream to the local unit stream power ( ${displaystyle Delta omega =omega _{local}-omega _{upstream}}$ ) to identify patterns such as sudden jumps or drops in stream power, these features can help identify locations where the local terrain controls the flow or widens out as well as areas prone to erosion.^[7]^[8]

Bridge and culvert design[edit]

Stream power can be used as an indicator of potential damages to bridges as a result of large rain events and how strong bridges should be designed in order to avoid damage during these events.^[9] Stream power can also be used to guide culvert and bridge design in order to maintain healthy stream morphology in which fish are able to continuing traversing the water course and no erosion processes are initiated.^[18]

References[edit]

^ ^a ^b ^c Bagnold, Ralph A. (1966). «An approach to the sediment transport problem from general physics». Professional Paper. doi:10.3133/pp422i. ISSN 2330-7102.
^ Rubey, W. W. (1933). «Equilibrium-conditions in debris-laden streams». Transactions, American Geophysical Union. 14 (1): 497. doi:10.1029/tr014i001p00497. ISSN 0002-8606.
^ Knapp, Robert T. (1938). «Energy-balance in stream-flows carrying suspended load». Transactions, American Geophysical Union. 19 (1): 501. doi:10.1029/tr019i001p00501. ISSN 0002-8606.
^ Bagnold, Ralph A. (1956-12-18). «The flow of cohesionless grains in fluids». Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 249 (964): 235–297. doi:10.1098/rsta.1956.0020. ISSN 0080-4614. S2CID 124012787.
^ ^a ^b ^c ^d ^e Gartner, John (2016-01-01). «Stream Power: Origins, Geomorphic Applications, and GIS Procedures». Water Publications.
^ Rhoads, Bruce L. (May 1987). «Stream Power Terminology». The Professional Geographer. 39 (2): 189–195. doi:10.1111/j.0033-0124.1987.00189.x. ISSN 0033-0124.
^ ^a ^b ^c ^d Bizzi, S.; Lerner, D. N. (January 2015). «The Use of Stream Power as an Indicator of Channel Sensitivity to Erosion and Deposition Processes: SP AS AN INDICATOR OF EROSION AND DEPOSITION». River Research and Applications. 31 (1): 16–27. doi:10.1002/rra.2717. S2CID 129164405.
^ ^a ^b Gartner, John D.; Dade, William B.; Renshaw, Carl E.; Magilligan, Francis J.; Buraas, Eirik M. (November 2015). «Gradients in stream power influence lateral and downstream sediment flux in floods». Geology. 43 (11): 983–986. doi:10.1130/G36969.1. ISSN 0091-7613.
^ ^a ^b Anderson, Ian; Rizzo, Donna M.; Huston, Dryver R.; Dewoolkar, Mandar M. (May 2017). «Stream Power Application for Bridge-Damage Probability Mapping Based on Empirical Evidence from Tropical Storm Irene». Journal of Bridge Engineering. 22 (5): 05017001. doi:10.1061/(ASCE)BE.1943-5592.0001022. ISSN 1084-0702.
^ Wilcock, Peter R. (April 1993). «Critical Shear Stress of Natural Sediments». Journal of Hydraulic Engineering. 119 (4): 491–505. doi:10.1061/(asce)0733-9429(1993)119:4(491). ISSN 0733-9429.
^ Petit, F.; Gob, F.; Houbrechts, G.; Assani, A. A. (2005-07-01). «Critical specific stream power in gravel-bed rivers». Geomorphology. 69 (1): 92–101. doi:10.1016/j.geomorph.2004.12.004. ISSN 0169-555X.
^ ^a ^b Petit, F.; Gob, F.; Houbrechts, G.; Assani, A. A. (2005-07-01). «Critical specific stream power in gravel-bed rivers». Geomorphology. 69 (1): 92–101. doi:10.1016/j.geomorph.2004.12.004. ISSN 0169-555X.
^ COSTA, JOHN E. (1983-08-01). «Paleohydraulic reconstruction of flash-flood peaks from boulder deposits in the Colorado Front Range». GSA Bulletin. 94 (8): 986–1004. doi:10.1130/0016-7606(1983)94<986:PROFPF>2.0.CO;2. ISSN 0016-7606.
^ ^a ^b Gartner, John (2016-01-01). «Stream Power: Origins, Geomorphic Applications, and GIS Procedures». Water Publications.
^ Jain, V.; Fryirs, K.; Brierley, G. (2008-01-01). «Where do floodplains begin? The role of total stream power and longitudinal profile form on floodplain initiation processes». Geological Society of America Bulletin. 120 (1–2): 127–141. doi:10.1130/B26092.1. ISSN 0016-7606.
^ Orr, H.G.; Large, A.R.G.; Newson, M.D.; Walsh, C.L. (August 2008). «A predictive typology for characterising hydromorphology». Geomorphology. 100 (1–2): 32–40. doi:10.1016/j.geomorph.2007.10.022.
^ Brookes, Andrew (1987). «The distribution and management of channelized streams in Denmark». Regulated Rivers: Research & Management. 1 (1): 3–16. doi:10.1002/rrr.3450010103. ISSN 1099-1646.
^ Kosicki, Andrzej J.; Davis, Stanley R. (January 2001). «Consideration of Stream Morphology in Culvert and Bridge Design». Transportation Research Record: Journal of the Transportation Research Board. 1743 (1): 57–59. doi:10.3141/1743-08. ISSN 0361-1981. S2CID 109792586.

Источник

1.3.3 Схемы и компоновка гидроузлов.

History[edit]

Derivation[edit]

Various Forms[edit]

(Total) Stream power[edit]

Total Stream Power[edit]

Unit (or Specific) Stream power[edit]

Critical Unit Stream Power[edit]

Relationships to other variables[edit]

Size of displaced sediment[edit]

Shear stress[edit]

Applications[edit]

Landscape evolution[edit]

Predicting flood plain formation[edit]

Sensitivity to erosion[edit]

Bridge and culvert design[edit]

See also[edit]

References[edit]

Не пропустите также: