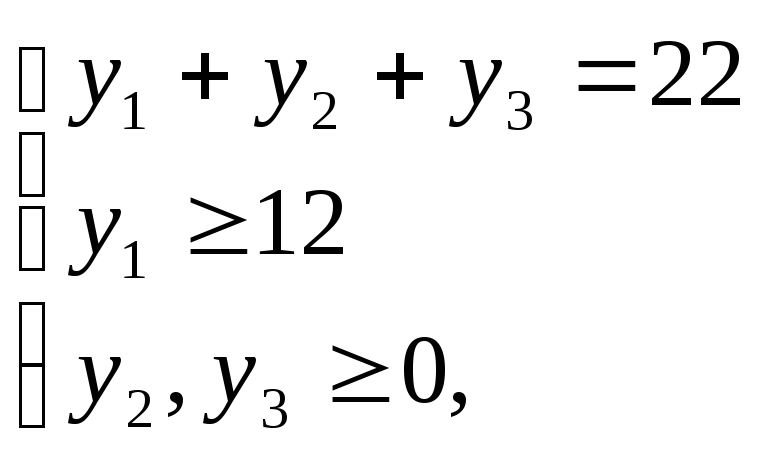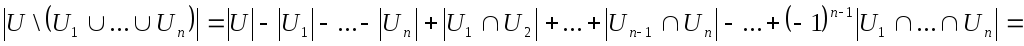-
Формула включения и исключения.
Чтобы
найти мощность объединения двух
непересекающихся множеств
нужно
просто сложить их мощности:
.
Если
множества пересекаются,
то
при сложении их мощностей каждый элемент
пересечения будет посчитан дважды.
Поэтому для правильного ответа необходимо
из суммы мощностей вычесть мощность их
пересечения:
.
При этом каждый элемент объединения
будет посчитан ровно один раз.
Пусть
теперь имеется три множества:
Теперь при сложении
мощностей всех трех множеств каждый
элемент, входящий ровно в два множества,
будет посчитан дважды, а каждый элемент,
входящий во все три множества, – трижды.
Если из суммы мощностей вычесть мощности
попарных пересечений, то по одному разу
будут посчитаны элементы, входящие
ровно в одно множество и ровно в два
множества, но элементы, входящие во все
три множества, не будут посчитаны ни
разу. Поэтому для получения правильного
ответа необходимо еще прибавить мощность
пересечения всех трех множеств:
Аналогичная
формула справедлива и в общем случае:
Докажем
эту формулу, называемую формулой
включения и исключения. Пусть элемент
входит ровно в
подмножеств
.
Вклад, который дает этот элемент в правую
часть, равен
,
как
это следует из тождества 4 для биномиальных
коэффициентов (п. 1.2.). Поэтому вклад
каждого элемента в правую часть будет
равен единице, т.е. правая часть будет
равна полному числу элементов, что и
доказывает формулу.
В
практических задачах часто имеется
некоторое множество U
и система его подмножеств U1,…,Um.
Требуется найти число элементов множества
U,
не принадлежащих ни одному из множеств
U1,…,Um
. В этом случае формула включения и
исключения выглядит следующим образом
.
Рассмотрим
пример. В группе, состоящей из 20 человек,
6 знают немецкий, 7 – французский и 8 –
английский язык, 3 человека знают немецкий
и французский, 4 – немецкий и английский,
5 – французский и английский и один
человек знает все 3 языка. Сколько человек
не знают ни одного иностранного языка?
Решение:
20-(6+7+8)+(3+4+5)-1=10.
Другой
пример. Пусть требуется найти число
натуральных чисел, не превосходящих
100 и не делящихся ни на одно из чисел 3,
5, 7. Число чисел, делящихся на 3, равно
[100/3]=33; на 5 – [100/5]=20; на 7 – [100/7]=14. Число
чисел, делящихся на 3 и 5, равно [100/15]=6; на
3 и 7 – [100/21]=4, на 5 и 7 – [100/35]=2. Число
чисел, делящихся на все три числа 3, 5 и
7, равно [100/105]=0. Поэтому искомое число
равно 100–(33+20+14)+(6+4+2)–0=45.
Рассмотрим
теперь пример посложнее. Пусть требуется
найти число целочисленных решений
системы
Формула
включения и исключения оказывается
полезной и здесь. Введем новые переменные
,
,
.
Система перепишется в виде
Пусть
U
– множество решений системы
U1
– множество решений системы
U2
– множество решений системы
U3
– множество решений системы
согласно
п. 1.1.
Чтобы
найти мощность множества U1,
достаточно в соответствующей системе
сделать замену
.
Это дает
.
Аналогично,
,
.
Далее,
легко видеть, что
,
,
.
Поэтому
в соответствии с формулой включения и
исключения число решений исходной
системы равно
В
качестве ещё одного примера рассмотрим
известную задачу о беспорядках. Требуется
найти число перестановок чисел 1,2,…,n,
в которых никакое число i
не стоит на i
– ом месте. Всего перестановок
.
Перестановок, в которых числоi
стоит на i
– ом месте,
Перестановок, в которых два различных
числаi
и j
стоят на своих местах,
и т.д. По формуле включения и исключения
имеем
.
Отметим,
что выражение в скобках с ростом
стремится к
.
Вопросы
для самопроверки.
-
В
группе 5 студентов не занимается ни в
одной спортивной секции, 10 студентов
занимается ровно в одной из спортивных
секций, 6 судентов ходят в две секции и
один студент занимается в трех секциях.
Сколько всего студентов в группе?
а) 22;
б) 20; в) 25.
-
В
группе 25 студентов. Из них в бассейн
ходят 10 человек, в гимнастический зал
– 8 человек, в волейбольную секцию – 6
человек. При этом 4 человека ходят
одновременно в бассейн и на гимнастику,
3 человека – в бассейн и на волейбол и
2 человека – на гимнастику и на волейбол.
Один человек ходит во все три секции.
Сколько студентов группы не занимается
в спортивных секциях?
а) 12; б)
9; в) 11.
-
Сколько
натуральных чисел, не превосходящих
100, не делятся на 2 и 3? а) 30; б) 33;
в) 34.
Соседние файлы в папке Дискретная математика
- #
- #
Видеоурок: Некоторые
сведения из теории множеств.
Множество — совокупность объектов
произвольной природы, которая рассматривается как единое целое.
Способы задания множества

Стандартные обозначения
Множества принято обозначать прописными буквами латинского алфавита (A, B, C, …). Объекты,
входящие в состав множества, называются его элементами и обозначаются строчными латинскими буквами.


Круги Эйлера
Для наглядного изображения множеств используются круги Эйлера.
Точки внутри круга считаются элементами множества.
Подмножество
Если каждый элемент множества P принадлежит множеству М, то говорят, что P есть подмножество
М, и записывают: P ⊂ М

Само множество М является своим подмножеством: М ⊂ М
Пустое множество является подмножеством М:
∅ ⊂ М
Универсальное множество содержит все возможные подмножества одной природы.
Обозначается буквой U.

Пересечение множеств
Пересечением двух множеств X и Y называется множество их общих элементов.
Обозначается X ∩ Y.
Множества M и X не имеют общих элементов: M ∩ X = ∅
P подмножество множества М: М ∩ P = P
Пересечение множеств М и М: М ∩ М = М

Объединение множеств
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих
множеств и не содержащее никаких других элементов (X ∪ Y).
M ∪ ∅ = М
P подмножество множества М: М ∪ P = М
Объединение множеств М и М: М ∪ М = М
Примеры пересечения и объединения множеств


Пусть множество P является подмножеством множества М. Дополнением
P до М называется множество, состоящее из тех элементов М, которые не вошли в P. Обозначается не Р или P’.
Дополнение М до М: М’ = ∅
Дополнение пустого множества до М: ∅’ = М
Дополнение множества М до универсального: M ∪ M ’ = U
Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества X обозначается |X|.

Мощность любого конечного множества равно количеству элементов данного множества.
Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.
Формула включений-исключений
Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если
известны их мощности и мощности всех их пересечений (объединений).
Объединение множеств:

Мощность объединения двух множеств:

Мощность объединения трех множеств:

Множества не пересекаются:

Мощность пересечение двух множеств:

Мощность пересечение трех множеств:

Задача 1.
В зимний лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом, коньками или лыжами. При этом
многие из них занимаются несколькими видами спорта. Всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Умением кататься на лыжах и сноуборде могут похвастаться 8 ребят,
на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта. Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?
Решение:
Обозначим через S, L и K множество сноубордистов, лыжников и любителей коньков соответственно.
Тогда:
|S∪L∪K| =
|S| + |L| + |K| —
|S∩L| — |S∩K| — |L∩K| + |S∩L∩K|=
30+28+42-8-5-10+3=80 =>
100 — 80 = 20
Ответ: 20 старшеклассников.
Информатика, 10 класс. Урок № 10.
Тема — Некоторые сведения из теории множеств
Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором, создателем теории множеств.

Георг Кантор
(1845—1918)
Немецкий математик, создатель теории множеств
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое. Под множеством мы можем понимать: учеников класса, фрукты, деревянные предметы, числа и т. д.
Например:
|
|
Множество учеников класса |
|
|
Множество деревянных предметов |
|
|
Множество чисел |
|
|
Множество фруктов |
Множества принято обозначать прописными буквами латинского алфавита (A,B,C,D и т. д.).
Множество можно задать перечислением всех его элементов, заключенных в фигурные скобки:
|
|
|
|
A={Маша, Ваня, Петя….} |
B={Банан, яблоко, виноград….} |
|
|
|
|
C={миска, подставка под карандаши, разделочная доска….} |
D={1,2,3,4,5….} |
Из некоторых элементов одного множества можно составить новое. Тогда такое множество Е принято называть подмножеством D:
D={1,2,3,4,5,6,7,8…}
E={2,4,6,8…}
Для наглядности множества можно изображать в виде окружности, так называемых кругов Эйлера, где элементы, входящие в множество, изображают внутри круга, а остальные вне:
Пересечением множеств называется множество их общих элементов.
Например:
Пусть множество A будет состоять из элементов 1,3,6,9,12,15, а множество B из элементов 2,4,6,8,10,12. Тогда в пересечение этих множеств будет входить 2,6,12:
A={1,3,6,9,12,15}
B={2,4,6,8,10,12}
A⋂B={2,6,12}
Множество может не содержать элементы, тогда оно будет называться пустым.
Если множества не имеют общих элементов, то их пересечение — пустое множество:
С⋂D=ø
Объединением двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов:
A={1,3,6,9}
B={2,4,6,8}
A⋃B={1,2,3,4,6,8,9}
Разностью множеств А и В называется множество элементов, принадлежащих множеству А, которые не принадлежат множеству В:
A={1,3,6,9}
B={2,4,6,8}
AB={1,3,9}
Если множество А является подмножеством B, то дополнением называется разность множества А и В:
A={2,4,6}
B={1,2,3,4,5,6}
Мощностью множества называется число его элементов: A={1,2,3,4,5,6}
|A|=5
Таким образом, мощность непересекающихся множеств будет являться суммой мощностей каждого множества:
A={1,3,5,7}
B={2,4,6,8}
|A⋃B|=8
Для вычисления мощности пересекающихся множеств можно использовать принцип включений и исключений:
|A⋃B|= |A|+|B|–| A⋂B|
A={1,2,3,4,5,6}
B={2,4,6,8}
|A⋃B|=6+4–3=7
Для вычисления мощности пересечения трех множеств принцип включений и исключений выглядит так:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|-|B⋂C|+|A⋂B⋂C|
Задание №1.
В классе 17 пловцов, 8 борцов и 13 футболистов. Известно, что в классе 25 детей, а ребят занимающихся футболом и плаваньем — 10, борьбой и плаваньем — 3, борьбой и футболом — 2 и только один ребенок занимается всеми тремя видами спорта. Сколько детей в классе не занимаются спортом?
Дано:
|A|=17, |B|=8, |C|=13
|A⋂B|=3, |A⋂C|=10, |B⋂C|=2
|A⋂B⋂C|=1
по формуле включения:
|A⋃B⋃С|= |A|+|B|+|C|–|A⋂B|–|A⋂C|–|B⋂C|+|A⋂B⋂C|=17+8+13–3–10–2+1=24
Таким образом, в классе 24 ребенка занимаются хотя бы одним видом спорта, ответ 1
Задание №2.
- Множество общих элементов двух множеств
- Совокупность объектов произвольной природы, которая рассматривается как единое целое
- Число элементов множества
- Множество элементов, не входящих в подмножество
- Множество, состоящее из всех элементов двух (или более) множеств и не содержащее никаких других элементов
Проверьте свои ответы:
- Пересечение
- Множество
- Мощность
- Дополнение
- Объединение
Задание №3
Закрасьте область цветом:
- Зеленым — R(PQ)
- Красным — (P⋂R)Q
- Желтым — (P∪Q)R
Ваше решение должно быть таким:
Информатика. 10 класса. Босова Л.Л. Оглавление
§ 17. Некоторые сведения из теории множеств
17.1. Понятие множества
С понятием множества вы познакомились на уроках математики ещё в начальной школе, а затем работали с ним при изучении математики и информатики в основной школе.
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Примерами множеств могут служить: множество всех учеников вашего класса, множество всех жителей Санкт-Петербурга, множество всех натуральных чисел, множество всех решений некоторого уравнения и т. п.
Множества принято обозначать прописными буквами латинского алфавита (А, В, С, …). Объекты, входящие в состав множества, называются его элементами.
Множество можно задать следующими способами:
1) перечислением всех его элементов;
2) характеристическим свойством его элементов.
В первом случае внутри фигурных скобок перечисляются все объекты, составляющие множество. Каждый объект, входящий в множество, указывается в фигурных скобках лишь один раз.
Например, запись М = {1, 3, 5, 7, 9} означает, что множество М состоит из чисел 1, 3, 5, 7 и 9. Точно такой же смысл будет иметь запись М = {3, 1, 5, 9, 7}. Иначе говоря, порядок расположения элементов в фигурных скобках значения не имеет. Важно точно указать, какие именно объекты являются элементами множества.
Например:
• число 5 является элементом множества М: 5 ? М 1);
• число 4 не является элементом множества М: 4 ? М.
1) Символ ? называется знаком принадлежности.
Это же множество можно задать с помощью характеристического свойства образующих его элементов — такого свойства, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. В нашем примере можно говорить о множестве натуральных однозначных нечётных чисел.
В рассматриваемом множестве М содержится 5 элементов. Это обозначают так: |М| = 5. Можно составить множество, содержащее любое число элементов. Например, множество всех корней уравнения х2 — 4х — 5 = 0 конечно (два элемента), а множество всех точек прямой бесконечно. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом ?.
Первый способ задания множеств применим только для конечных множеств, да и то при условии, что число элементов множества невелико. Вторым способом можно задавать как конечные, так и бесконечные множества.
Из некоторых элементов множества М можно составить новое множество, например Р: Р = {1, 3, 5}.
Если каждый элемент множества Р принадлежит множеству М, то говорят, что Р есть подмножество М, и записывают: Р ? М.
Само множество М является своим подмножеством, т. к. каждый элемент М принадлежит множеству М. Пустое множество также является подмножеством М.
Работая с объектами какой-то определённой природы, всегда можно выделить «самое большое» или универсальное множество, содержащее все возможные подмножества. Пусть А — множество чётных чисел, В — множество натуральных чисел, С — множество чисел, кратных пяти.
Тогда самым большим множеством, содержащим в себе множества А, В и С, а также другие подобные множества, будет множество целых чисел. Универсальное множество будем обозначать буквой U.
Для наглядного изображения множеств используются круги Эйлера (рис. 4.1). Точки внутри круга считаются элементами множества.

Рис. 4.1. Графическое изображение множеств: 1) х ? М, 2) х ? М
17.2. Операции над множествами
Над множествами, как и над числами, производят некоторые операции.
Пересечением двух множеств X и Y называется множество их общих элементов.
Пересечение множеств обозначают с помощью знака ?: Х ? У. На рисунке 4.2 закрашено множество X ? Y.

Рис. 4.2. Графическое изображение множества X ? Y
Пусть множества X и Y состоят из букв:
X = {ш к, о, л, а};
У = {у, р, о, к}.
Эти множества имеют общие элементы: к, о.
X ? У = { к, о}.
Множества М и X не имеют общих элементов, их пересечение — пустое множество:
М ? Х = ?.
Пересечение множеств М и Р есть множество Р, а пересечение множеств М и М есть множество М:
М ? Р = Р;
М ? М = М.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Объединение множеств обозначают с помощью знака ?: X ? У.
На рисунке 4.3 закрашено множество X ? У.

Рис. 4.3. Графическое изображение множества X ? У
Для наших примеров:
Х ? У = {ш, к, о, л, а, у, р};
М ? X = {1, 3, 5, 7, 9, ш, к, о, л, а};
М ? Р = М; М ? М = М.
Подумайте, возможно ли равенство: А ? В = А ? В.
Пересечение и объединение выполняются для любой пары множеств. Третья операция — дополнение — имеет смысл не для всех множеств, а только тогда, когда второе множество является подмножеством первого.
Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.
Дополнение Р до М обозначают
= {7, 9}.
Дополнение М до М есть пустое множество, дополнение пустого множества до М есть
Особый интерес представляет дополнение некоторого множества В до универсального множества U. Например, если В — это множество точек, принадлежащих некоторому отрезку, то его дополнением
до универсального множества U, которым в данном случае является множество всех точек числовой прямой, является множество точек, не принадлежащих данному отрезку.
В общем случае можем записать:
(рис. 4.4)

Рис. 4.4. Дополнение множества В до универсального множества
На рисунке 4.5 видно, что множество А ? В будет совпадать с универсальным, если А будет совпадать с множеством
или содержать его в качестве подмножества. В первом случае, т. е. при А =
мы имеем дело с минимальным множеством А, таким что A ? В = U.

Рис. 4.5. Выбор такого множества А, что А ? В = U
Каким должно быть множество А для того, чтобы множество
? В совпадало с универсальным множеством?
Для ответа на этот вопрос воспользуйтесь рисунком 4.6.

Рис. 4.6. Выбор такого множества А, что ? В = U
17.3. Мощность множества
Мощностью конечного множества называется число его элементов.
Мощность множества X обозначается |Х|.
В рассмотренных выше примерах |Х| = 5, |М| = 5.
Число элементов объединения двух непересекающихся множеств равно сумме чисел элементов этих множеств. Так, в объединении множеств М и X содержится 10 элементов: |М ? Х| = 10.
Если же множества пересекаются, то число элементов объединения находится сложнее. Так, X состоит из 5 элементов, множество Y — из 4, а их объединение — из 7. Сложение чисел 5 и 4 даёт нам число 9. Но в эту сумму дважды вошло число элементов пересечения. Чтобы получить правильный результат, надо к числу элементов X прибавить число элементов Y и из суммы вычесть число элементов пересечения. Полученная формула подходит для любых двух множеств: |Х ? Y| = |Х| + |Y| — |Х ? Y|. Это частный случай так называемого принципа включений-исключений.
Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).
Для случая объединения трёх множеств формула имеет вид:
Аналогичные формулы справедливы и для пересечения множеств:

Пример. В зимний оздоровительный лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом, коньками или лыжами. При этом многие из них занимаются не одним, а двумя и даже тремя видами спорта. Организаторы выяснили, что всего кататься на сноуборде умеют 30 ребят, на лыжах — 28, на коньках — 42. Всего умением кататься на лыжах и сноуборде из них могут похвастаться 8 ребят, на лыжах и коньках — 10, на сноуборде и коньках — 5, но только трое из них владеют всеми тремя видами спорта.
Сколько ребят не умеет кататься ни на сноуборде, ни на лыжах, ни на коньках?
Обозначим через S, L и К множества сноуборд истов, лыжников и любителей коньков соответственно. Тогда |S| = 30, |L| = 28 и |К| = 42. При этом |S ? L| = 8, |К ? L| = 10, |S ? К| = 5, |S ? L ? K| = 3.
Объединение множеств S, L и К — это множество ребят, увлекающихся хотя бы каким-то видом спорта.
По формуле включений-исключений находим:
|S ? L ? К| = 30 + 28 + 42 — 8 — 10 — 5 + 3 = 80.
Таким образом, из 100 старшеклассников 20 не умеют кататься ни на сноуборде, ни на лыжах, ни на коньках.
САМОЕ ГЛАВНОЕ
Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое.
Пересечением двух множеств X и Y называется множество их общих элементов.
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Пусть множество Р является подмножеством множества М. Дополнением Р до М называется множество, состоящее из тех элементов М, которые не вошли в Р.
Мощностью конечного множества называется число его элементов.
Формула включений-исключений позволяет вычислить мощность объединения (пересечения) множеств, если известны их мощности и мощности всех их пересечений (объединений).
Вопросы и задания
1. Если множество X — это множество натуральных чисел, делящихся нацело на 2, а У — множество натуральных чисел, делящихся нацело на 3, то что будет
2. Пусть множество X — это множество натуральных чисел, делящихся нацело на 18, a Y — множество натуральных чисел, делящихся нацело на 14. Укажите наименьшее число, входящее
3. Пусть А, В и С — некоторые множества, обозначенные кругами, U — универсальное множество.
4. В первую смену в лагере «Дубки» отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. При этом 10 человек были и отличниками, и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличниками, и спортсменами, и победителями олимпиад. Сколько ребят отдыхало в лагере?
5. Старшеклассники заполняли анкету с вопросами об экзаменах по выбору. Оказалось, что выбрали они информатику, физику и обществознание. В классе 38 учеников. Обществознание выбрал 21 ученик, причём трое из них выбрали ещё и информатику, а шестеро — ещё и физику. Один ученик выбрал все три предмета. Всего информатику выбрали 13 учеников, пятеро из которых указали в анкете два предмета. Надо определить, сколько же учеников выбрали физику.
*6. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Сколько человек знают все три языка?
§ 16. Кодирование звуковой информации
Глава 4. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И АЛГЕБРЫ ЛОГИКИ
§ 17. Некоторые сведения из теории множеств
§ 18. Алгебра логики