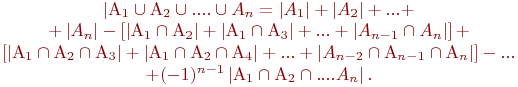Как найти мощность перечисления множеств

Множество –
совокупность определенных различаемых
объектов, для которых можно установить
принадлежит данный объект множеству
или нет.

Число элементов
конечного множества М называется его
мощностью |М|.

1. Мощность объединения
   двух множеств:

2. Мощность объединения
   трех множеств:

3. Мощность объединения
   N
   множеств:

Пример:

1. Векторы. Прямое произведение множеств. Мощности прямого произведения множеств.

Вектор (или кортеж)
— это упорядоченный набор элементов.
Элементы вектора называются координатами
или компонентами. Число координат —
длина вектора (размерность).

Координаты вектора
могут совпадать. Два вектора равны, если
они имеют одинаковую длину и равны
соответствующие координаты.

Прямым (декартовым)
произведением множеств А и В (А x
В) называется множество всех векторов
(a,
b),
таких, что a
∈
A,
b
∈
B:

Если А=В, то А х
А=А².

Прямым произведением
множества

называется множество всех векторов
длины m,
таких, что

.

Пусть

— конечные множества. Соответственно
мощности этих множеств равны:

.

Тогда мощность
прямого произведения N
множеств равна произведению мощностей
соответствующих множеств, т.е.

.

1. Отношения. Основные понятия отношений (отношения; унарные, бинарные, n-местные отношения)

Отношения – один
из способов задания связи между элементами
множества.

Унарные или
одноместные отношения – отражают
наличие определенного признака Р у
элемента множества М.

Тогда все такие
элементы a
из множества М, которые отличаются
данным признаком R,
образующие подмножества в М, называются
унарными отношением R.

Бинарные отношения
– используются для определения
взаимосвязи, которыми характеризуются
парные элементы во множестве М.

Тогда все пары вида
(a,
b)
из множества М, между которыми имеют
отношения, образ подмножества пар из
всех пар элементов М х М=М²,
называется бинарным отношением М.

Могут рассматриваться
N-местные
отношения. Под N-местными
отношениями понимают подмножество R
прямого произведения N
множеств, n:
R
М₁
х М₂
х…х М_n,
элементы a₁,
a₂,…,a_n,
где (а₁
принадл М₁
и т.д.) находятся в отношении R,
если (а1, а2,…,аn)
принадл. R.

1. Отношения. Бинарные отношения. Основные понятия (определение, обозначения, область определения, область значений, способы задания бинарных отношений). Привести примеры.

Отношения – один
из способов задания связи между элементами
множества.

Бинарным отношением
R из множества A в множество B называется
подмножество прямого произведения A и
B и обозначается:

D(R)
– область определения. ={a:
(a,
b)
∈R}

Q(R)
– область значения. ={b:
(a, b) ∈R}

Первый способ
задания множества состоит в 1
непосредственном перечислении таких
пар. Ясно, что он приемлем лишь в случае
конечного множества R.

Второй удобный
способ задания отношения R
на конечном множестве — матричный. Все
элементы нумеруются, и матрица отношения
R
определяется своими элементами для
всех i
и j.
Известным примером такого задания
отношений являются турнирные таблицы
(если ничьи обозначить нулями, как и
проигрыш, то матрица изобразит отношение
«xi
— победитель yj»).

1. Отношения.
   Свойства бинарных отношений
   (рефлексивность, антирефлексивность,
   симметричность, антисимметричность,
   транзитивность). Привести примеры.
   Графические особенности диаграммы
   (бинарное отношение задано в виде
   диаграммы состоящей из узлов и стрелок)
   в зависимости от характера свойств
   бинарного отношения.

Отношения – один
из способов задания связи между элементами
множества.

1. В математике
   бинарное отношение R на множестве X
   называется рефлексивным, если всякий
   элемент этого множества находится в
   отношении R с самим собой.

1. В математике
   бинарное отношение R на множестве X
   называется антирефлексивным, если
   всякий элемент этого множества не
   находится в отношении R с самим собой.

1. В математике
   бинарное отношение R на множестве X
   называется симметричным, если для
   каждой пары элементов множества (a,b)
   выполнение отношения
   

   влечёт выполнение отношения
   
   .

1. В математике
   бинарное отношение R на множестве X
   называется антисимметричным, если для
   каждой пары элементов множества a,b
   выполнение отношений aRb и bRa влечёт a =
   b, или, что то же самое, выполнение
   отношений aRb и bRa возможно только для
   равных a и b.

1. В математике
   бинарное отношение R на множестве X
   называется транзитивным, если для любых
   трёх элементов множества a,b,c выполнение
   отношений aRb и bRc влечёт выполнение
   отношения aRc.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Мощность множества

Множество равномощно множеству , если существует биекция .

Из того, что существует биекция , следует, что соответствие есть биекция на . Поэтому если равномощно , то и равномощно , и мы можем говорить, что множества и равномощны.

Факт равномощности множеств и будем записывать так: .

Из определения равномощности и свойств биекции также следует, что для любого множества имеет место (тождественное отображение есть биекция множества на себя); а для любых множеств из и следует (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть отношение эквивалентности, заданное на «множестве всех множеств» (на самом деле на множестве всех подмножеств некоторого универсального множества).

Примечание. Зачастую в литературе по теории множеств равномощные множества и называют «эквивалентными множествами». Однако следует различать общее понятие отношения эквивалентности и его частный случаи — эквивалентность, или равномощность, множеств.

Если мы обозначим через класс эквивалентности множества по отношению , то утверждение о равномощности множеств и можно записать так: .

Этот класс эквивалентности называют мощностью множества .

Конечные множества и равномощны тогда и только тогда, когда множества и состоят из одного и того же числа элементов, т.е. . Отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству. Это свойство конечных множеств можно сформулировать так.

Теорема 1.8. Если — конечное множество и — инъекция, то она является сюръекцией и, следовательно, биекцией.

В силу приведенных выше соображений мощностью конечного множества можно считать натуральное число , так как, задавая такое число, мы задаем и класс всех (попарно равномощных) множеств вида . Обратно, каждый такой класс однозначно определяет натуральное число как число элементов в каждом множестве данного класса. Естественно считается, что мощность пустого множества равна нулю.

Перейдем теперь к исследованию мощности бесконечных множеств. Таковы хорошо известные нам ещё со школы числовые множества и .

Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают (читается «алеф нуль»).

Любую биекцию называют нумерацией счетного множества ; если элемент есть для некоторого , то этот элемент обозначаем через , называя натуральное число номером элемента относительно данной нумерации .

Таким образом, элементы счетного множества можно перенумеровать, записав их в виде последовательности или . Другими словами, счетное множество есть область значений некоторой функции натурального аргумента.

Пример 1.21. а. Множество всех нечетных натуральных чисел счетно. Нумерацию можно задать так:

б. Множество всех натуральных чисел, делящихся на заданное число , счётно. Нумерацию можно задать так: . В частности, при получаем, что множество всех четных чисел счётно. Этот и предыдущий примеры показывают, что бесконечное (счетное) множество может иметь собственное равномощное ему подмножество.

в. Множество всех целых чисел счётно. Нумерацию можно установить так:

Свойства счётных множеств

Рассмотрим свойства счетных множеств.

Теорема 1.9. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Пусть — бесконечное множество. Значит, оно не пусто и существует элемент . Положим . Множество не пусто, так как в противном случае имело бы место равенство , что противоречит предположению о бесконечности . Выберем элемент и положим

Множество также не пусто, поскольку иначе мы бы имели и множество было бы конечным.

Методом математической индукции можно показать, что для любого множество , где , не пусто. Тогда существует элемент и . Таким образом, все элементы , попарно различны и множество счетно, а его нумерация может быть задана так: .

Теорема 1.10. В любом бесконечном множестве можно выделить два не пересекающихся между собой счетных подмножества.

Доказательство. Разобьем множество натуральных чисел на два подмножества:

(множество нечетных чисел),
(множество четных чисел).

Оба этих множества счетны (см. пример 1.21).

Согласно теореме 1.9, бесконечное множество содержит некоторое счетное подмножество . Пусть установлена некоторая его нумерация. Разобьем это подмножество на два подмножества: всех элементов с четными и всех элементов с нечетными номерами. По построению эти подмножества не пересекаются и являются счетными, поскольку счётны множества четных и нечетных чисел.

Теорема 1.11. Любое подмножество счетного множества конечно или счетно.

Доказательство.Пустое подмножество конечно по определению. Пусть — счетное множество, а — его некоторое непустое подмножество. Поскольку множество счетно, можно считать, что задана некоторая его нумерация. Следовательно, каждый элемент подмножества имеет свой номер. Запишем номера элементов множества в порядке возрастания: . Если среди них есть наибольший номер , то подмножество конечно. В противном случае получим счетное подмножество , нумерация которого установлена так: .

Если множество конечно или счетно, его называют не более чем счетным. Семейство множеств называют не более чем счетным, если множество (индексов) не более чем счетно.

Теорема 1.12. Объединение любого не более чем счетного семейства счетных множеств счетно.

Пусть — конечное или счетное семейство счетных множеств. Рассмотрим сначала случай, когда множества попарно не пересекаются.

В этом случае нумерация объединения конечного семейства счетных множеств может быть проведена по схеме, изображенной на рис. 1.14, а нумерация объединения счетного семейства счетных множеств — по схеме, приведенной на рис. 1.15.

Пусть теперь — произвольное счетное семейство счетных множеств, т.е. множества могут пересекаться. В этом случае, применяя указанные на рис. 1.14 и 1.15 схемы нумерации к конечному или счетному объединению счетных множеств, следует пропускать каждый раз элементы, которые уже получили номера.

Полезно отметить также и следующий факт.

Теорема 1.13. Объединение конечного и счетного множеств счетно.

Теорема 1.14. Пусть — бесконечное множество, а — его не более чем счетное подмножество. Если множество бесконечно, то оно равномощно множеству .

По теореме 1.10 в множестве , поскольку оно бесконечно, можно выбрать счетное подмножество . Ясно, что . Множество является счетным как объединение двух счетных множеств или объединение счетного и конечного множеств. Поэтому существует биекция . Поскольку

то требуемую биекцию на строим так: на подмножестве , общем для и , эта биекция совпадает с тождественным отображением; на подмножестве эта биекция есть биекция .

Следствие 1.1. Если — бесконечное множество, а — не более чем счетное множество, то .

Существуют бесконечные множества, не являющиеся счетными. Это вытекает из следующих рассуждений.

Рассмотрим множество всех последовательностей нулей и единиц, т.е. последовательностей вида

, где для каждого .

Обозначим множество таких «двоичных» последовательностей через .

Теорема Кантора

Теорема 1.15 (Кантора). Множество не есть счетное множество.

Пусть множество и счетное. Тогда существует биекция . Выпишем все последовательности

Построим последовательность : положим , если , и , если . Ясно, что эта последовательность не совпадает ни с одной из последовательностей , а это противоречит допущению, что любая последовательность из есть для некоторого .

Итак, не равномощно .

В то же время содержит подмножество последовательностей, в каждой из которых только один член отличен от нуля. Это подмножество равномощно множеству всех одноэлементных подмножеств и, следовательно, самому . Следовательно, множество бесконечно, но не равномощно счетному множеству и потому не является счетным.

Теорема 1.16. Множество всех подмножеств множества натуральных чисел и множество равномощны.

Определим отображение множества на множество следующим образом: если , то при и при .

Тем самым подмножеству ставится в соответствие последовательность , i-й член которой равен единице тогда и только тогда, когда число есть элемент множества . Докажем, что — биекция на .

Покажем, что отображение — инъекция. Пусть и — различные подмножества . Тогда найдется число или число . В первом случае в последовательности i-й член будет равен единице, а в последовательности — нулю. Таким образом, . Во втором случае и опять . Следовательно, отображение — инъекция.

Покажем, что — сюръекция. Возьмем произвольную последовательность . Образуем множество . Ясно, что . Таким образом, для любой последовательности существует подмножество , такое, что . Следовательно, — сюръекция.

Таким образом, мы показали, что — биекция, а множества и равномощны.

Множество мощности континуум (континуальное множество)

Мощность множества обозначают и называют мощностью континуума, а любое множество, эквивалентное множеству , называют множеством мощности континуума или континуальным множеством.

Теорема 1.17. Множество действительных чисел отрезка равномощно множеству всех последовательностей нулей и единиц .

Каждое действительное число из отрезка представим в виде бесконечной дроби в двоичной системе счисления. Число 1 представим в виде периодической дроби, содержащей бесконечное число единиц — . Конечные рациональные дроби представим как бесконечные, дополнив справа бесконечным числом нулей. Таким образом, каждое число из представлено в виде последовательности нулей и единиц. Кроме этого, выбросим счетное множество всех периодических дробей вида , поскольку каждая такая дробь представляет то же самое число, что и дробь , где для всякого . Легко видеть, что полученное таким образом множество двоичных дробей равномощно множеству .

Следствие 1.2. .

Выше была доказана равномощность множеств и . Тогда имеем .

Теорема 1.18. Следующие множества равномощны:

1) множество действительных чисел отрезка ;
2) множество действительных чисел интервала ;
3) множество действительных чисел отрезка ;
4) множество действительных чисел интервала ;
5) множество действительных чисел (числовая ось) ;
6) множество всех подмножеств множества натуральных чисел .

Покажем равномощность множеств и . Из множества действительных чисел отрезка выделим двухэлементное подмножество . Разностью этих множеств будет множество действительных чисел интервала , и, согласно теореме 1.14, .

Отображение задает биекцию множества на множество . Следовательно, эти множества равномощны. Заметим, что аналогично доказывается равномощность и .

Покажем, что . Биекцию можно установить, например, с помощью функции .

Поскольку равномощность и 2W ранее доказана, имеем

Замечание 1.7. Заметим, что если в условиях теоремы 1.14 множество несчетно, а — его счетное подмножество, то множество бесконечно, ибо иначе получилось бы, что множество счетно как объединение конечного и счетного множеств.

Таким образом, можно утверждать, что для любого несчетного множества и его не более чем счетного подмножества имеет место равенство .

Сравнение мощностей множеств

До сих пор речь шла о равенстве мощностей. Однако мощности разных множеств можно в определенном смысле сравнивать, говоря о большей или меньшей мощности.

Считают, что мощность множества не превышает мощность множества , если равномощно некоторому подмножеству множества . Можно показать, что из соотношений и следует, что .

Мощность множества считается строго меньшей мощности множества , если множества и неравномощны и существует собственное подмножество множества , равномощное множеству , то есть

и .

Можно доказать, что из и следует .

Таким образом, на множестве всех мощностей (т.е. на множестве всех классов эквивалентности по отношению ) установлено отношение порядка.

Из определения сразу следует, что мощность любого конечного множества строго меньше мощности , а из доказательства теоремы 1.15 вытекает, что . Кроме того, согласно теореме 1.9, мощность счетного множества является наименьшей на множестве всех бесконечных мощностей (т.е. мощностей бесконечных множеств). Можно сказать, что всякое бесконечное множество не менее чем счетно.

Без доказательства приведем две важные теоремы.

Теорема Кантора–Бернштейна

Теорема 1.19 (Кантора–Бернштейна). Для любых двух множеств и имеет место в точности одно из следующих трех условий: либо , либо , либо .

Таким образом, любые два множества сравнимы по мощности. Другими словами, «шкала мощностей» линейно упорядочена.

Теорема 1.20. Для любого множества верно неравенство .

В силу теоремы 1.20 нет наибольшей мощности, так как для любого множества существует множество большей мощности — его булеан. Заметим, что для счетного множества теорема 1.20 сводится к теореме Кантора 1.15.

Теорема 1.21 (теорема о квадрате). Для любого бесконечного множества его декартов квадрат равномощен самому множеству .

Доказательство проведем для частных случаев счетного и континуального множеств.

Сначала обратимся к счетному множеству. Для доказательства утверждения достаточно показать, что , т.е. задать на некоторую нумерацию. Рассмотрим множество упорядоченных пар. Это множество счетно по построению. Легко видеть, что справедливо равенство

откуда, согласно теореме 1.12, вытекает счетность декартова квадрата множества как счетного объединения счетных множеств.

Перейдем к континуальному множеству. Докажем, что множество всех упорядоченных пар двоичных последовательностей эквивалентно множеству всех таких последовательностей, т.е. .

Паре последовательностей поставим в соответствие последовательность

Это соответствие будет взаимно однозначным, т.е. установлена биекция между и .

Получается, что — как это ни удивительно — в квадрате «столько же» точек, сколько и в каждой его стороне. Можно обобщить это утверждение для произвольной конечной декартовой степени множества .

Следствие 1.3. Множество рациональных чисел счетно.

Каждому рациональному числу, представленному несократимой дробью , однозначно соответствует упорядоченная пара , и, напротив, любая упорядоченная пара взаимно простых целых чисел и однозначно определяет несократимую дробь и, значит, рациональное число. Следовательно, множество эквивалентно некоторому бесконечному подмножеству множества . Поскольку множество счетно, из теоремы 1.11 вытекает, что любое его бесконечное подмножество счетно. Таким образом, множество счетно.

В заключение приведем сводку результатов по мощностям некоторых конечных множеств.

Теорема 1.22. Если и — конечные множества и , a , то:

1) мощность множества всех отображений в равна ;
2) мощность множества всех биекций из на себя равна
3) мощность множества всех инъекций из в равна ;
4) мощность множества всех подмножеств множества равна ;
5) мощность множества всех k-элементных подмножеств множества равна ;
6) мощность прямого произведения равна .

Напомним, что в комбинаторике число называют числом перестановок элементов, число — числом размещений без повторений из элементов по , число (обозначаемое также ) — числом сочетаний из элементов по . Эти числа называются также биномиальными коэффициентами, поскольку

(формула бинома Ньютона).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Достаточно часто в математической науке возникает ряд трудностей и вопросов, причем многие ответы не всегда проясняются. Не исключением стала такая тема, как мощность множеств. По сути, это не что иное как численное выражение количества объектов. В общем смысле множество является аксиомой, у него нет определения. В основе лежат любые объекты, а точнее их набор, который может носить пустой, конечный или бесконечный характер. Кроме этого, он содержит числа целые или натуральные, матрицы, последовательности, отрезки и прямые.

О существующих переменных

Нулевой или пустой набор, не имеющий собственного значения, считается элементом мощности, так как это подмножество. Сбор всех подмножеств непустого множества S является множеством множеств. Таким образом, набор мощности заданного множества считается многим, мыслимым, но единым. Это множество называется множеством степеней S и обозначается P (S). Если S содержит N элементов, то P (S) содержит 2 ^ n подмножеств, так как подмножество P (S) является либо ∅, либо подмножеством, содержащим r элементов из S, r = 1, 2, 3, … Составленное из всего бесконечного множества M называется степенным количеством и символически обозначается P (M).

Элементы теории множеств

Эта область знаний была разработана Джорджем Кантором (1845-1918 годы жизни). Сегодня она используется почти во всех отраслях математики и служит ее фундаментальной частью. В теории множеств элементы представлены в форме списка и заданы типами (пустой набор, одноэлементный, конечные и бесконечные множества, равные и эквивалентные, универсальные), объединение, пересечение, разность и дополнение чисел. В повседневной жизни часто говорится о коллекции таких объектов, как куча ключей, стая птиц, пачка карточек и т. д. В математике 5 класса и не только, встречаются натуральные, целые, простые и составные числа.

Можно рассмотреть следующие множества:

• натуральные числа;
• буквы алфавита;
• первичные коэффициенты;
• треугольники с разными значениями сторон.

Видно, что эти указанные примеры представляют собой четко определенные множества объектов. Рассмотрим еще несколько примеров:

• пять самых известных ученых мира;
• семь красивых девушек в обществе;
• три лучших хирурга.

Эти примеры мощности множества не являются четко определенными коллекциями объектов, потому, что критерий «наиболее известных», «самых красивых», «лучших» варьируется от человека к человеку.

Наборы

Это значение представляет собой четко определенное количество различных объектов. Предположив, что:

• набор слов является синонимом, агрегатом, классом и содержит элементы;
• объекты, члены являются равными по значению терминами;
• наборы обычно обозначаются прописными буквами A, B, C;
• элементы набора представлены маленькими буквами a, b, c.

Если «a» — элемент множества A, то говорится, что «a» принадлежит A. Обозначим фразу «принадлежит» греческим символом «∈» (epsilon). Таким образом, выходит, что a ∈ A. Если ‘b’ — элемент, который не принадлежит A, это представляется как b ∉ A. Некоторые важные наборы, используемые в математике 5 класса, представляют, используя три следующих метода:

• заявки;
• реестров или табличные;
• правило создания построения.

При детальном рассмотрении форма заявления основана на следующем. В этом случае задано четкое описание элементов множества. Все они заключены в фигурные скобки. Например:

• множество нечетных чисел, меньших 7 — записывается как {меньше 7};
• набор чисел больше 30 и меньше 55;
• количество учеников класса, вес которых больше, чем учителя.

В форме реестра (табличной) элементы набора перечислены в паре скобок {} и разделены запятыми. Например:

1. Пусть N обозначает множество первых пяти натуральных чисел. Следовательно, N = → форма реестра
2. Набор всех гласных английского алфавита. Следовательно, V = {a, e, i, o, u, y} → форма реестра
3. Множество всех нечетных чисел меньше 9. Следовательно, X = {1, 3, 5, 7} → форма реестра
4. Набор всех букв в слове «Математика». Следовательно, Z = {M, A, T, H, E, I, C, S} → Форма реестра
5. W — это набор последних четырех месяцев года. Следовательно, W = {сентябрь, октябрь, ноябрь, декабрь} → реестр.

Стоит отметить, что порядок, в котором перечислены элементы, не имеет значения, но они не должны повторяться. Установленная форма построения, в заданном случае правило, формула или оператор записываются в пару скобок, чтобы набор был корректно определен. В форме set builder все элементы должны обладать одним свойством, чтобы стать членом рассматриваемого значения.

В этой форме представления набора элемент множества описывается с помощью символа «x» или любой другой переменной, за которой следует двоеточие («:» или «|» используется для обозначения). Например, пусть P — множество счетных чисел, большее 12. P в форме set-builder написано, как — {счетное число и больше 12}. Это будет читаться определенным образом. То есть, «P – множество элементов x, такое, что x является счетным числом и больше 12».

Решенный пример с использованием трех методов представления набора: количество целых чисел, лежащих между -2 и 3. Ниже приведены примеры различных типов наборов:

1. Пустой или нулевой набор, который не содержит какого-либо элемента и обозначается символом ∅ и считывается как phi. В форме списка ∅ имеет написание {}. Пустым является конечное множество, так как число элементов 0. Например, набор целых значений меньше 0.
2. Очевидно, что их не должно быть <0. Следовательно, это пустое множество.
3. Набор, содержащий только одну переменную, называется одноэлементным множеством. Не является ни простым, ни составным.

Конечное множество

Множество, содержащее определенное число элементов, называется конечным либо бесконечным множеством. Пустое относится к первому. Например, набор всех цветов в радуге.

Бесконечное количество – это набор. Элементы в нем не могут быть перечислены. То есть, содержащий подобные переменные, называется бесконечным множеством. Примеры:

• мощность множества всех точек в плоскости;
• набор всех простых чисел.

Но стоит понимать, что все мощности объединения множества не могут быть выражены в форме списка. К примеру, вещественные числа, так как их элементы не соответствуют какой-либо конкретной схеме.

Кардинальный номер набора – это число различных элементов в заданном количестве A. Оно обозначается n (A).

Например:

1. A {x: x ∈ N, x <5}. A = {1, 2, 3, 4}. Следовательно, n (A) = 4.
2. B = набор букв в слове ALGEBRA.

Эквивалентные наборы для сравнения множеств

Две мощности множества A и B являются таковыми, если их кардинальное число одинаково. Символом для обозначения эквивалентного набора является «↔». Например: A ↔ B.

Равные наборы: две мощности множества A и B, если они содержат одни и те же элементы. Каждый коэффициент из A является переменной из B, и каждый из B является указанным значением A. Следовательно, A = B. Различные типы объединения множеств в мощности и их определения объясняются с помощью указанных примеров.

Сущность конечности и бесконечности

Каковы различия между мощностью конечного множества и бесконечного?

Для первого значения характерно следующее название, если оно либо пустое, либо имеет конечное число элементов. В конечном множестве переменная может быть указана, если она имеет ограниченный счет. Например, с помощью натурального числа 1, 2, 3. И процесс листинга заканчивается на некотором N. Число различных элементов, отсчитываемых в конечном множестве S, обозначается через n (S). А также называется порядком или кардинальным. Символически обозначается по стандартному принципу. Таким образом, если множество S является русским алфавитом, то оно содержит в себе 33 элемента. Также важно запомнить, что элемент не встречается более одного раза в наборе.

Бесконечное количество в множестве

Множество называется бесконечным, если элементы не могут быть перечислены. Если оно имеет неограниченное (то есть несчетное) натуральное число 1, 2, 3, 4 для любого n. Множество, которое не является конечным, называется бесконечным. Теперь можно обсудить примеры рассматриваемых числовых значений. Варианты конечного значения:

1. Пусть Q = {натуральные числа меньше 25}. Тогда Q — конечное множество и n (P) = 24.
2. Пусть R = {целые числа между 5 и 45}. Тогда R — конечное множество и n (R) = 38.
3. Пусть S = {числа, модуль которых равен 9}. Тогда S = {-9, 9} является конечным множеством и n (S) = 2.
4. Набор всех людей.
5. Количество всех птиц.

Примеры бесконечного множества:

• количество существующих точек на плоскости;
• число всех пунктов в сегменте линии;
• множество положительных целых чисел, кратных 3, является бесконечным;
• все целые и натуральные числа.

Таким образом, из приведенных выше рассуждений понятно, как различать конечные и бесконечные множества.

Мощность множества континуум

Если провести сравнение множества и других существующих значений, то к множеству присоединено дополнение. Если ξ – универсальное, а A – подмножество ξ, то дополнение к A является количеством всех элементов ξ, которые не являются элементами A. Символически обозначается дополнение A относительно ξ как A’. К примеру, 2, 4, 5, 6 являются единственными элементами ξ, которые не принадлежат A. Следовательно, A’= {2, 4, 5, 6}

Множество с мощностью континуум имеет следующие особенности:

• дополнением универсального количества является пустое рассматриваемое значение;
• эта переменная нулевого множества является универсальным;
• количество и его дополнение являются непересекающимися.

Например:

1. Пусть количество натуральных чисел является универсальным множеством и А – четное. То, тогда A ‘{x: x – множество нечетное с такими же цифрами}.
2. Пусть ξ = множество букв в алфавите. A = набор согласных. Тогда A ‘= количество гласных.
3. Дополнением к универсальному множеству является пустое количество. Можно обозначить через ξ. Тогда ξ ‘= Множество тех элементов, которые не входят в ξ. Пишется и обозначается пустое множество φ. Поэтому ξ = φ. Таким образом, дополнение к универсальному множеству является пустым.

В математике «континуум» иногда используется для обозначения реальной линии. И в более общем плане, для описания подобных объектов:

• континуум (в теории множеств) — вещественная линия или соответствующее кардинальное число;
• линейный — любое упорядоченное множество, которое разделяет определенные свойства реальной прямой;
• континуум (в топологии) — непустое компактное связное метрическое пространство (иногда хаусдорфово);
• гипотеза о том, что никакие бесконечные множества больше целых чисел, но меньшие, чем действительные числа;
• мощность континуума — кардинальное число, представляющее размер множества действительных чисел.

По существу дела, континуум (измерение), теории или модели, которые объясняют постепенные переходы из одного состояния в другое без каких-либо резких изменений.

Проблемы объединения и пересечения

Известно, что пересечение двух или более множеств – это количество, содержащее все элементы, которые являются общими в этих значениях. Задачи Word на множествах решаются, чтобы получить основные идеи о том, как использовать свойства объединения и пересечения множеств. Решенные основные проблемы слов на множествах выглядят так:

1. Пусть A и B – два конечных множества. Они представляют собой такие, что n (A) = 20, n (B) = 28 и n (A ∪ B) = 36, находится n (A ∩ B).

Связь в наборах с использованием диаграммы Венна:

1. Объединение двух множеств может быть представлено заштрихованной областью, представляющей A ∪ B. A ∪ B, когда A и B – непересекающиеся множества.
2. Пересечение двух множеств может быть представлено диаграммой Венна. С затененной областью, представляющей A ∩ B.
3. Разность двух наборов может быть представлена диаграммами Венна. С заштрихованной областью, представляющей A — B.
4. Связь между тремя наборами, использующими диаграмму Венна. Если ξ представляет универсальное количество, то A, B, C – три подмножества. Здесь все три набора являются перекрывающимися.

Обобщение информации о множестве

Мощность множества определяется как общее количество отдельных элементов в наборе. А последнее указанное значение описывается как количество всех подмножеств. При изучении подобных вопросов требуются методы, способы и варианты решения. Итак, у мощности множества примерами могут служить следующие:

Пусть A = {0,1,2,3}| | = 4, где | A | представляет мощность множества A.

Теперь можно найти свой набор мощности. Это тоже довольно просто. Как уже сказано, набор мощности установлен из всех подмножеств заданного количества. Поэтому нужно в основном определить все переменные, элементы и другие значения A, которые {}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, { 2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}.

Теперь мощность выясняет P = {{}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, {2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}}, который имеет 16 элементов. Таким образом, мощность множества A = 16. Очевидно, что это утомительный и громоздкий метод решения этой проблемы. Однако есть простая формула, по которой, непосредственно, можно знать количество элементов в множестве мощности заданного количества. | P | = 2 ^ N, где N — число элементов в некотором A. Эта формула может быть получена применением простой комбинаторики. Таким образом, вопрос равен 2 ^ 11, поскольку число элементов в множестве A равно 11.

Итак, множеством является любое численно выраженное количество, которое может быть всевозможным объектом. К примеру, машины, люди, числа. В математическом значении это понятие шире и более обобщенное. Если на начальных этапах разбираются числа и варианты их решения, то в средних и высших стадиях условия и задачи усложнены. По сути, мощность объединения множества определена принадлежностью объекта к какой-либо группе. То есть один элемент принадлежит к классу, но имеет одну или несколько переменных.

Некоторые сведения о мощности множества приведены в [I].
Здесь мы рассмотрим это понятие более подробно.

Множество А равномощно множеству И, если существует
биекцил f:A→B.

Из того, что существует биекция f:A→B, следует, что
соответствие f^-1 есть биекция В на А (см. 1,4). Поэтому если
А равномощно В, то и В равномощно A, и мы можем говорить,
что множества АиВ равномощны.

Факт равномощности множеств А и В будем записывать
так: А~В.

Из определения равномощности и свойств биекции также
следует, что для любого множества А имеет место А ~ А
(тождественное отображение есть биекция множества А на
себя); а для любых множеств А, В, С из А~В и В~С следует
А~С (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть
отношение эквивалентности*, заданное на „множестве всех
множеств» (на самом деле на множестве всех подмножеств
некоторого универсального множества).

*Зачастую в литературе по теории множеств равномощные множества
и называют „эквивалентными множествами». Однако следует различать
общее понятие отношения эквивалентности и его частный случаи —
эквивалентность, или равномощность, множеств.

Если мы обозначим через |А| класс эквивалентности
множества А по отношению ~, то утверждение о равномощности
множеств Аи В можно записать так: |А| = |В|.

Этот класс эквивалентности |А| называют мощностью
множества А.

Конечные множества А = {а₁,.., а_n} и В = {b₁ ,…, b_n} равномощны тогда и только тогда, когда множества А и В состоят
из одного и того же числа элементов, т.е. n = m. Отсюда, в
частности, следует, что конечное множество не является
номощным никакому своему собственному подмножеству. Это
свойство конечных множеств можно сформулировать так.

Теорема 1.8. Если А — конечное множество и f:A→B
→ А — инъекция, то она является сюръекцией и, следовательно,
биекцией. #

В силу приведенных выше соображений мощностью
конечного множества А = {а₁,.., а_n} можно считать натуральное
число n, так как, задавая такое число, мы задаем и класс всех
(попарно равномощных) множеств вида {а₁,.., а_n}. Обратно,
каждый такой класс однозначно определяет натуральное число
п как число элементов в каждом множестве данного класса.
Естественно считается, что мощность пустого множества
равна нулю.

Перейдем теперь к исследованию мощности бесконечных
множеств. Таковы хорошо известные нам числовые множества
ℕ, ℤ, ℚ, ℝ и ℂ.

Любое множество, равномощное множеству всех
натуральных чисел, называют счетным. Мощность счетного множества
обозначают ℵ₀ (читается „алеф нуль»).

Любую биекцию v: ℕ → М называют нумерацией
счетного множества М; если элемент М есть v(n) для некоторого
n ∈ ℕ, то этот элемент М обозначаем через a_n, называя
туральное число n номером элемента a_n относительно данной
нумерации v.

Таким образом, элементы счетного множества можно
перенумеровать, записав их в виде последовательности а₁,.., а_n, … или {a_n}_n∈ℕ Другими словами, счетное множество есть
область значений некоторой функции натурального аргумента.

Пример 1.21. а. Множество всех нечетных натуральных
чисел счетно. Нумерацию v можно задать так: v(n) = 2n — 1,

б. Множество всех натуральных чисел, делящихся на
заданное число k ≥ 2, счетно. Нумерацию v можно задать так:
v(n) = kn, n∈ℕ. В частности, при k = 2 получаем, что
множество всех четных чисел счетно. Этот и предыдущий
примеры показывают, что бесконечное (счетное) множество может
иметь собственное равномощное ему подмножество.

в. Множество ℤ всех целых чисел счетно. Нумерацию
можно установить так:

Рассмотрим свойства счетных множеств.

Теорема 1.9. Любое бесконечное множество содержит
счетное подмножество.

◀ Пусть М₀ — бесконечное множество. Значит, оно не пусто
и существует элемент а₁ ∈ М₀. Положим М₁ = М₀ {a₁}.
Множество М₁ не пусто, так как в противном случае имело бы
место равенство М₀ = {a_i}, что противоречит предположению
о бесконечности М₀. Выберем элемент а₂ ∈ М₁ и положим
М₂ = М₁ {а₂} = М₀ {a₁, а₂}. Множество М₂ также не пусто,
поскольку иначе мы бы имели М₀ = {a₁, а₂} и множество
было бы конечным.

Методом математической индукции можно показать, что
для любого n ≥ 1 множество М_n = M₀ {a₁,…, a_n}, где а₁ ∈ М₀, …, a_n ∈ М_n-1, не пусто. Тогда существует элемент
a_n+1 ∈ М_n и a_n+1 ∉ M_n+1 = М_n {а_n+1}. Таким образом, все
элементы a_n, n ∈ ℕ, попарно различны и множество {а_n:n ∈ ℕ}
счетно, а его нумерация может быть задана так: v(n) = а_n.

Теорема 1.10. В любом бесконечном множестве можно
выделить два не пересекающихся между собой счетных
подмножества.

◀ Разобьем множество натуральных чисел на два
подмножества: ℕ₁ = {n: n = 2k — 1, k ∈ ℕ} (множество нечетных чисел),
и ℕ₂ = {n: n = 2k, k ∈ ℕ} (множество четных чисел). Оба эти
множества счетны (см. пример 1.21).

Согласно теореме 1.9, бесконечное множество содержит
некоторое счетное подмножество А. Пусть установлена
некоторая его нумерация. Разобьем это подмножество на два
подмножества: всех элементов с четными и всех элементов с
нечетными номерами. По построению эти подмножества не
пересекаются и являются счетными, поскольку счетны множества
четных и нечетных чисел. >

Теорема 1.11. Любое подмножество счетного множества
конечно или счетно.

◀ Пустое подмножество конечно по определению. Пусть М —
счетное множество, а В — его некоторое непустое
подмножество. Поскольку множество М счетно, можно считать, что
задана некоторая его нумерация. Следовательно, каждый
элемент подмножества В имеет свой номер. Запишем номера
элементов множества В в порядке возрастания: i₁, …, i_n, …

Если среди них есть наибольший номер i_p, то подмножество
В конечно. В противном случае получим счетное
подмножество {a_i1, a_i2,…, a_in,…}, нумерация которого установлена так:
v(n) = a_in.

Если множество конечно или счетно, его называют не
более чем счетным. Семейство (А_i)_i∈I множеств называют
не более чем счетным, если множество (индексов) I не более
чем счетно.

Теорема 1.12. Объединение любого не более чем счетного
семейства счетных множеств счетно.

<4 Пусть (А_i)_i∈I — конечное или счетное семейство счетных
множеств. Рассмотрим сначала случай, когда множества А_i
попарно не пересекаются.

В этом случае нумерация объединения конечного семейства
счетных множеств может быть проведена по схеме,
изображенной на рис. 1.14, а нумерация объединения счетного семейства
счетных множеств — по схеме, приведенной на рис. 1.15.

Пусть теперь (А_n)_n∈ℕ — произвольное счетное семейство
счетных множеств, т.е. множества А_i могут пересекаться. В
этом случае, применяя указанные на рис. 1.14 и 1.15 схемы
нумерации к конечному или счетному объединению счетных
множеств, следует пропускать каждый раз элементы, которые
уже получили номера. >

Полезно отметить также и следующий факт.

Теорема 1.13. Объединение конечного и счетного
множеств счетно. #

Теорема 1.14. Пусть М — бесконечное множество, а N —
его не более чем счетное подмножество. Если множество MN
бесконечно, то оно равномощно множеству М.

◀ По теореме 1.10 в множестве MN, поскольку оно
бесконечно, можно выбрать счетное подмножество N’. Ясно, что
N∩N’ = ∅. Множество N∪N’ является счетным как
объединение двух счетных множеств или объединение счетного и
конечного множеств. Поэтому существует биекция f: N∪N’ → N’.
Поскольку (M(N∪N’))∪(N∪N’)=M, M (N∪N’)∪N’ =
= MN, то требуемую биекцию М на МN строим так: на
подмножестве М (N∪N’), общем для М N и М, эта биекция
совпадает с тождественным отображением; на подмножестве
N∪N’ эта биекция есть биекция f. ▶

Следствие 1.1. Если М — бесконечное множество, а N —
не более чем счетное множество, то М ~ М ∪ N.

Существуют бесконечные множества, не являющиеся
счетными. Это вытекает из следующих рассуждений.

Рассмотрим множество всех последовательностей нулей и
единиц, т.е. последовательностей вида {α₁,α₂, …,α_n,…}, где
α_i ∈ {0,1} для каждого i ≥ 1.

Обозначим множество таких „двоичных»
последовательностей через {0,1}^ω.

Теорема 1.15 (теорема Кантора). Множество {0,1}^ω
не есть счетное множество.

◀ Пусть множество {0,1}^ω счетное. Тогда существует биекция
φ: ℕ → {0,1}^ω. Выпишем все последовательности φ(n):

φ(1) = {α₁₁,α₁₂, …,α_1n,…},

φ(1) = {α₁₁,α₁₂, …,α_1n,…},

………………………………………………………

φ(n) = {α_n1,α_n2, …,α_nn,…},

………………………………………………………

Построим последовательность β = {β₁,…, β_n,…}: положим
β_i = 1, если α_ii = 0, и β_i = 0, если α_ii = 1. Ясно, что эта
последовательность не совпадает ни с одной из последовательностей
φ(n), а это противоречит допущению, что любая
последовательность из {0,1}^ω есть φ(k) для некоторого k.

Итак, ℕ не равномощно {0,1}^ω.

В то же время {0,1}^ω содержит подмножество
последовательностей, в каждой из которых только один член отличен
от нуля. Это подмножество равномощно множеству всех
одноэлементных подмножеств ℕ и, следовательно, самому ℕ.
Следовательно, множество {0,1}^ω бесконечно, но не равномощно
счетному множеству и потому не является счетным. ▶

Теорема 1.16. Множество 2^ℕ всех подмножеств множества
натуральных чисел и множество {0,1}^ω равномощны.

◀ Определим отображение φ множества 2^ℕ на множество
{0,1}^ω следующим образом: если X ⊆ ℕ, то φ(Х)_i = 1 при i ∈ X
и φ(Х)_i = 0 при i ∉ X.

Тем самым подмножеству X ставится в соответствие
последовательность φ(Х), i-й член которой равен единице тогда
и только тогда, когда число i есть элемент множества X.
Докажем, что φ — биекция 2^ℕ на {0,1}^ω.

Покажем, что отображение φ — инъекция. Пусть X и Y —
различные подмножества ℕ. Тогда найдется число i ∈ X Y или
число j ∈ YX. В первом случае в последовательности φ(Х) i-й
член будет равен единице, а в последовательности φ(Y) — нулю.
Таким образом, φ(Х) ≠ φ(Y). Во втором случае φ(Y)_j = 1,
φ(Х)_j = 0 и опять φ(Х) ≠ φ(Y). Следовательно, отображение
φ — инъекция.

Покажем, что φ — сюръекция. Возьмем произвольную
последовательность α ∈ {0,1}^ω. Образуем множество Х_α =
= {i: α_i = 1}. Ясно, что φ(Х_α) = α. Таким образом, для
любой последовательности α ∈ {0,1}^ω существует подмножество
Х_α ∈ 2^ℕ, такое, что φ(Х_α) = α. Следовательно, φ —
сюръекция.

Таким образом, мы показали, что φ — биекция, а множества
2^ℕ и {0,1}^ω равномощны. >

Мощность множества 2^ℕ обозначают с и называют
мощностью континуума, а любое множество, эквивалентное
множеству 2^ℕ, называют множеством мощности
континуума или континуальным множеством.

Теорема 1.17. Множество действительных чисел отрезка
[0,1] равномощно множеству всех последовательностей нулей и
единиц {0,1}^ω.

◀ Каждое действительное число из отрезка [0,1] представим в
виде бесконечной дроби в двоичной системе счисления. Число 1
представим в виде периодической дроби, содержащей
бесконечное число единиц — 0,1(1). Конечные рациональные дроби
представим как бесконечные, дополнив справа бесконечным
числом нулей. Таким образом, каждое число из [0,1] представлено
в виде последовательности нулей и единиц. Кроме этого,
выбросим счетное множество всех периодических дробей вида
O,α₀α₁…α_kO(1), поскольку каждая такая дробь представляет
то же самое число, что и дробь O,α₀α₁…α_k1(0), где α_i ∈ {0,1}
для всякого i = 1,k. Легко видеть, что полученное таким
образом множество двоичных дробей равномощно множеству
{0,1}^ω▶

Следствие 1.2. [0,1] ~ 2^ℕ.

◀ Выше была доказана равномощность множеств (0,1)^ω и 2^ℕ.
Тогда имеем [0,1] ~ {0,1}^ω ~ 2^ℕ. ▶

Теорема 1.18. Следующие множества равномощны:

1. множество действительных чисел отрезка [0,1];
2. множество действительных чисел интервала (0,1);
3. множество действительных чисел отрезка [а, b];
4. множество действительных чисел интервала (а, b);
5. множество действительных чисел (числовая ось) ℝ;
6. множество всех подмножеств множества натуральных
   чисел 2^ℕ.

◀ Покажем равномощность множеств [0,1] и (0,1). Из
множества действительных чисел отрезка [0,1] выделим
двухэлементное подмножество {0,1}. Разностью этих множеств будет
множество действительных чисел интервала (0,1), и, согласно
теореме 1.14, [0,1] ~ (0,1).

Отображение у = (b — a)х + а задает биекцию множества
[0,1] на множество [а, b]. Следовательно, эти множества
номощны. Заметим, что аналогично доказывается
равномощность (0,1) и (а, b).

Покажем, что (0,1) ~ ℝ. Биекцию можно установить,
например, с помощью функции у = 1/πarctgx + 1/2.

Поскольку равномощность [0,1] и 2^ℕ ранее доказана, имеем

[0,1] ~ (0,1) ~ [а, b] ~ (а, b) ~ ℝ ~ 2^ℕ. ▶

Замечание 1.7. Заметим, что если в условиях теоремы 1.14
множество М несчетно, а N — его счетное подмножество, то
множество MN бесконечно, ибо иначе получилось бы, что
множество М = (М N) U N счетно как объединение конечного
и счетного множеств.

Таким образом, можно утверждать, что для любого
несчетного множества М и его не более чем счетного подмножества
N имеет место равенство |М N| = |М|. #

До сих пор речь шла о равенстве мощностей. Однако
мощности разных множеств можно в определенном смысле
сравнивать, говоря о большей или меньшей мощности.

Считают, что мощность множества А не превышает
мощность множества В (|А| ≤ |В|), если А равномощно некоторому
подмножеству множества В. Можно показать, что из
соотношений |A| ≤ |В| и |В| ≤ |А| следует, что |A| = |B|.

Мощность множества А считается строго меньшей
мощности множества В (|А| < |В|), если множества А и В
мощны и существует собственное подмножество С множества
В, равномощное множеству А, т.е. (А ≁ В) и (∃С ⊂ В)(А~С).

Можно доказать, что из |А| ≤ |В| и |В| ≤ |С| следует |А| ≤
|С|. Таким образом, на множестве всех мощностей (т.е.
на множестве всех классов эквивалентности по отношению ~)
установлено отношение порядка.

Из определения сразу следует, что мощность любого
конечного множества строго меньше мощности Но, а из
доказательства теоремы 1.15 вытекает, что ℵ₀ < с. Кроме того,
согласно теореме 1.9, мощность счетного множества ℵ₀
является наименьшей на множестве всех бесконечных мощностей (т.е.
мощностей бесконечных множеств). Можно сказать, что
всякое бесконечное множество не менее чем счетно.

Без доказательства приведем две важные теоремы.

Теорема 1.19 (теорема Кантора — Бернштейна).
Для любых двух множеств А и В имеет место в точности одно
из следующих трех условий: либо |А| < |B|, либо |В| < |А|, либо
|B| = |А| #

Таким образом, любые два множества сравнимы по
мощности. Другими словами, „шкала мощностей» линейно
упорядочена.

Теорема 1.20. Для любого множества А верно неравенство
|2^ℕ| > |А|. #

В силу теоремы 1.20 нет наибольшей мощности, так как для
любого множества А существует множество большей
мощности — его булеан. Заметим, что для счетного множества А
теорема 1.20 сводится к теореме Кантора 1.15.

Теорема 1.21 (теорема о квадрате). Для любого
бесконечного множества М его декартов квадрат М × М
мощен самому множеству М.

◀ Доказательство проведем для частных случаев счетного и
континуального множеств.

Сначала обратимся к счетному множеству. Для
доказательства утверждения достаточно показать, что ℕ × ℕ ~ ℕ, т.е.
задать на ℕ × ℕ некоторую нумерацию. Рассмотрим множество
A_i = {(i, j): j ∈ ℕ} упорядоченных пар. Это множество счетно
по построению. Легко видеть, что справедливо равенство

откуда, согласно теореме 1.12, вытекает счетность декартова
квадрата ℕ × ℕ множества ℕ как счетного объединения
счетных множеств.

Перейдем к континуальному множеству. Докажем, что
множество всех упорядоченных пар двоичных последовательностей
эквивалентно множеству всех таких последовательностей, т.е.
2^ℕ × 2^ℕ ~ 2^ℕ.

Паре последовательностей (α, β) поставим в соответствие
последовательность α₀, β₀, α₁, β₁, …, α_n, β_n, … Это
соответствие будет взаимно однозначным, т.е. установлена биекция
между 2^ℕ × 2^ℕ ~ 2^ℕ. ▶

Получается, что — как это ни удивительно — в квадрате
„столько же» точек, сколько и в каждой его стороне. Можно
обобщить это утверждение для произвольной конечной
декартовой степени множества М.

Следствие 1.3. Множество рациональных чисел ℚ счетно.

◀ Каждому рациональному числу, представленному
несократимой дробью a/b, однозначно соответствует упорядоченная пара
(а, b), и, напротив, любая упорядоченная пара (а, b) взаимно
простых целых чисел а и b однозначно определяет
несократимую дробь a/b и значит, рациональное число. Следовательно,
множество ℚ эквивалентно некоторому бесконечному
подмножеству множества ℤ × ℤ. Поскольку множество ℤ × ℤ счетно,
из теоремы 1.11 вытекает, что любое его бесконечное
подмножество счетно. Таким образом, множество ℚ счетно. >

В заключение приведем сводку результатов по мощностям
некоторых конечных множеств.

Теорема 1.22. Если М и N — конечные множества и
|М| = m, a |N| = n, то:

1. мощность множества всех отображений М в N равна n^m;
2. мощность множества всех биекций из N на себя равна P_n=n!;
3. мощность множества всех инъекций из М в N (m ≤ n) равна A^mn =       n!  (n-m)!      ;
4. мощность множества всех подмножеств множества N
   равна 2ⁿ;
5. мощность множества всех k-элементных подмножеств
   множества N равна C^kn =       n!  k!(n-k)!      ;
6. мощность прямого произведения М × N равна mn. #

Напомним [I], что в комбинаторике число Р_n называют
числом перестановок n элементов, число A^mn — числом
размещений без повторений из n элементов по m, число C^kn
(обозначаемое также (^nk )) — числом сочетаний из n элементов по k. Эти
числа называются также биномиальными коэффициентами, поскольку (формула бинома Ньютона).