Как найти мощность электрического тока
На данной странице калькулятор поможет рассчитать мощность электрического тока онлайн. Для расчета задайте напряжение, силу тока или сопротивление.
Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.
Через напряжение и силу тока
Формула для нахождения мощности электрического тока через напряжение и силу тока:
U — напряжение; I — сила тока.
Через напряжение и сопротивление

Формула для нахождения мощности электрического тока через напряжение и сопротивление:
U — напряжение; R — сопротивление.
Через силу тока и сопротивление

Формула для нахождения мощности электрического тока через силу тока и сопротивление:
I — сила тока; R — сопротивление.
Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
- P – активная мощность;
- U – напряжение приложенное к участку цепи;
- I — сила тока, протекающего через соответствующий участок.
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
Пример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:
Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0.74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
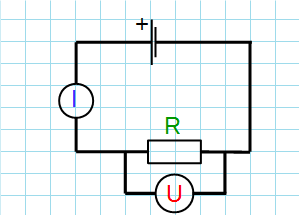
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт
Видео по теме
Как посчитать мощность тока
- Главная
- /
- Физика
- /
- Как посчитать мощность тока
Чтобы посчитать мощность тока (электрическую мощность) воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Мощность тока (Р) или электрическая мощность — физическая величина, которая характеризует скорость передачи или преобразования электрической энергии. В системе СИ единицей измерения мощности тока является ватт (Вт).
Найти мощность зная ток и напряжение
Напряжение: U =В
Сила тока: I =A
Мощность тока: P =
0
Вт
Формула
P = U ⋅ I
Пример
Если электрическое напряжение U = 12 В, а сила тока I = 5 А, то:
Электрическая мощность P = 12 ⋅ 5 = 60 Вт
Найти мощность зная ток и сопротивление
Сила тока: I =A
Сопротивление: R =Ом
Мощность тока: P =
0
Вт
Формула
P = I² ⋅ R
Пример
Если сила тока I = 5 А, а электрическое сопротивление R = 2 Ом, то:
Электрическая мощность P = 5² ⋅ 2 = 50 Вт
Найти мощность зная сопротивление и напряжение
Напряжение: U =В
Сопротивление: R =Ом
Мощность тока: P =
0
Вт
Формула
P = U²/R
Пример
Если электрическое напряжение U = 12 В, а электрическое сопротивление R = 2 Ом, то:
Электрическая мощность P = 12² : 2 = 72 Вт
См. также
Мощность электрического тока, формула
Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.
Если:
P — мощность электрического тока (Вт),
W — работа электрического тока (Дж = Вт·с),
U — напряжение (В),
I — сила тока (A),
R — сопротивление цепи (Ом),
t — время протекания тока (c),
То:
Мощность электрического тока через напряжение и ток
[ P = frac{W}{t} = UI ]
Мощность электрического тока, формула
Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.
Если:
P — мощность электрического тока (Вт),
W — работа электрического тока (Дж = Вт·с),
U — напряжение (В),
I — сила тока (A),
R — сопротивление цепи (Ом),
t — время протекания тока (c),
То:
Мощность электрического тока через напряжение и ток
[ P = frac{W}{t} = UI ]
Мощность электрического тока через напряжение и сопротивление
[ P = frac{U^2}{R} ]
Мощность электрического тока через ток и сопротивление
[ P = I^2 R ]
Мощность электрического тока через напряжение и сопротивление
[ P = frac{U^2}{R} ]
Мощность электрического тока через ток и сопротивление
[ P = I^2 R ]
Мощность электрического тока |
стр. 615 |
|---|
Электрическая мощность и закон Ома
Для анализа и расчета параметров нагревателей, как правило, мы используем различные методы, в частности закон Ома. Этот закон используется в основном для определения неизвестных величин, таких как напряжение, ток, сопротивление и мощность, которые связаны с одним или несколькими элементами электронной схемы. Закон Ома — основной закон теории электрических цепей, который определяет линейную зависимость между напряжением, током и сопротивлением. В данной статье мы постараемся подробно рассказать о законе Ома и его практическом применении.

Закон Ома
Закон Ома — это основной, главный и важный закон теории электрических цепей, который исследует взаимосвязь между напряжением, током и сопротивлением. В нем говорится, что при постоянной температуре ток, протекающий по цепи, прямо пропорционален напряжению или разности потенциалов в этой цепи.
В алгебраической форме, V∝ I
V = IR
Где
I — ток, протекающий по цепи, измеряется в амперах.
V — напряжение, приложенное к цепи, измеряется в вольтах.
А R — это константа пропорциональности, называемая сопротивлением, которое измеряется в омах.
Это сопротивление также указывается в килоомах, мегаомах и т. д.
Следовательно, закон Ома гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению в этой цепи. Закон Ома можно применить как к отдельным частям, так и ко всей цепи.
Математически ток, I = V/R
Напряжение, V = IR
Сопротивление, R = V/I
Треугольник закона Ома
Ниже показано, что отношение между различными величинами в законе Ома называется треугольником закона Ома. Это простой метод описания, а также простой для запоминания соотношения между напряжением, током и сопротивлением.

На приведенном выше рисунке показан треугольник закона Ома, где отдельные термины, такие как напряжение, ток и сопротивление, и их формулы представлены из основного уравнения закона Ома. На приведенном выше рисунке один параметр вычисляется из оставшихся двух параметров. Таким образом, можно сделать вывод, что при высоком сопротивлении ток будет низким, а ток будет высоким, когда сопротивление низкое, при любом приложенном напряжении.
Электрическая мощность
Электрическая мощность дает скорость, с которой энергия передается по цепи. Электрическая мощность измеряется в ваттах. Эта мощность потребляется, когда напряжение вызывает протекание тока в цепи.
Следовательно, электрическая мощность есть произведение напряжения и силы тока.
Математически P = VI
По закону Ома V = IR и I = V/R
Подставляя в уравнение мощности
P = I2 R
P = V2/ R
Следовательно, электрическая мощность, P =VI или I 2 R или V 2 / R
Это три основные формулы для нахождения электрической мощности в цепи. Таким образом, мощность может быть рассчитана, когда известна любая из двух величин.
Треугольник мощности
Подобно треугольнику закона Ома, на рисунке ниже показан треугольник мощности, чтобы показать соотношение между мощностью, напряжением и током. Уравнения отдельных параметров легко запоминаются по этому рисунку. Округлите и скройте параметр, который необходимо измерить, а положение оставшихся двух параметров дает уравнение для поиска скрытого или округленного параметра, как показано на рисунке ниже.

Круговая диаграмма закона Ома
В дополнение к двум вышеупомянутым концепциям существует еще один метод определения параметров схемы с использованием закона Ома, который представляет собой круговую диаграмму закона Ома. Используя круговую диаграмму закона Ома, можно легко запомнить все уравнения для нахождения напряжения, тока, сопротивления и мощности, которые необходимы для упрощения электрических цепей, которые могут быть простыми или сложными.

На приведенном выше рисунке показана круговая диаграмма, которая показывает взаимосвязь между мощностью, напряжением, током и сопротивлением. Эта диаграмма разделена на четыре блока для мощности, напряжения, сопротивления и тока. Каждый блок состоит из трех формул с двумя известными значениями для каждой формулы. Из диаграммы для нахождения каждого параметра в цепи мы можем использовать любую из трех доступных формул.
Графическое представление закона Ома
Для лучшего понимания этой концепции ниже приведена экспериментальная установка, в которой регулируемый источник напряжения с шестью ячейками (по 2 В каждая) подключен к нагрузочному резистору через переключатель выбора напряжения. Измерительные приборы, такие как вольтметр и амперметр, также подключены к цепи для измерения напряжения и тока в цепи.

Регулируемый источник напряжения с нагрузочным резистором
Сначала подключите резистор 10 Ом и установите переключатель в положение «1». Тогда амперметр показывает 0,2 А, а вольтметр показывает 2 В, потому что I = V/R, т. е. I = 2/10 = 0,2 А. Затем измените положение селекторного переключателя на вторую ячейку, чтобы подать 4 В на нагрузку и запишите показания амперметра. По мере того, как селектор будет постепенно изменяться от первого положения к последнему, мы получим текущие значения, такие как 0,2, 0,4, 0,6, 0,8, 1, 1,2 для значений напряжения 2, 4, 6, 8, 10 и 12 соответственно.
Точно так же поместите резистор 20 Ом вместо резистора 10 Ом и выполните ту же процедуру, что и выше. Мы получим значения тока 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 для значений напряжения 2, 4, 6, 8, 10 и 12В соответственно. Постройте график этих значений, как показано ниже.

Графическое представление закона Ома
На приведенном выше графике для данного напряжения ток меньше, когда сопротивление больше. Рассмотрим случай приложенного напряжения 12 В, когда значение тока составляет 1,2 А при сопротивлении 10 Ом и 0,6 Ом при сопротивлении 20 Ом. Точно так же при одном и том же токе напряжение тем больше, чем больше сопротивление. Из приведенных выше результатов следует, что отношение напряжения к току постоянно, когда сопротивление постоянно. Следовательно, зависимость между напряжением и током является линейной, и наклон этой линейной кривой становится тем круче, чем больше сопротивление.
Пример применения закона Ома
Рассмотрим приведенную ниже схему, в которой батарея на 6 В подключена к нагрузке 6 Ом. Амперметр и вольтметры подключены к цепи для измерения тока и напряжения практически. Но используя закон Ома мы можем найти силу тока и мощность следующим образом.

Из закона Ома
V = IR
I = V/R
I = 6/6
I = 1 А
Мощность, P = VI
P = 6×1
P = 6 Вт
Но практически амперметр не показывает точное значение из-за внутреннего сопротивления батареи. Включив внутреннее сопротивление батареи (предположим, что батарея имеет внутреннее сопротивление 1 Ом), текущее значение рассчитывается следующим образом.

Общее сопротивление цепи 6+1=7 Ом.
Ток, I = V/R
I = 6/7
I = 0,85 Ампер
Цепь фар в автомобиле
На приведенном ниже рисунке показана схема фар легкового автомобиля без схемы управления. С применением закона Ома мы можем узнать ток, протекающий через каждую лампу. Как правило, каждая лампочка подключается параллельно к аккумулятору, что позволяет другим элементам светиться, даже если какой-то из них поврежден. К этим параллельным лампам подводится батарея 12 В, где лампы имеют сопротивление 2,4 каждая (считается в данном случае).

Общее сопротивление цепи равно R = R1x R2/(R1 + R2), так как они соединены параллельно.
R = 5,76/4,8 = 1,2
Тогда ток, протекающий по цепи, равен I = V/R.
I = 12/1,2
I = 10А.
Ток, протекающий через отдельную лампу, равен I1 = I2 = 5 А (из-за одинаковых сопротивлений).
Закон Ома для цепей переменного тока
В общем, закон Ома можно применить и к цепям переменного тока . Если нагрузка индуктивная или емкостная, то также учитывается реактивное сопротивление нагрузки. Следовательно, с некоторыми изменениями закона Ома, учитывающими влияние реактивного сопротивления, его можно применять к цепям переменного тока. Из-за индуктивности и емкости в переменном токе будет значительный фазовый угол между напряжением и током. А также сопротивление переменному току называется импедансом и обозначается как Z.
Таким образом, закон Ома для цепей переменного тока задается как
E = IZ
I = E/Z
Z = E/I
Где E — напряжение в цепи переменного тока,
I — текущий ток,
Z — импеданс.
Все параметры в приведенном выше уравнении представлены в комплексной форме, которая включает фазовый угол. Подобно круговой диаграмме цепи постоянного тока, круговая диаграмма закона Ома для цепи переменного тока приведена ниже.

Пример закона Ома (цепи переменного тока)
Рассмотрим приведенную ниже схему, в которой нагрузка переменного тока (сочетание резистивной и индуктивной) подключена к источнику переменного тока 10 В, 60 Гц. Нагрузка имеет сопротивление 5 Ом и индуктивность 10 мГн.

Тогда значение импеданса нагрузки Z = R + jX L
Z = 5 + j (2∏ × f × L)
Z = 5+ j (2×3,14×60×10×10-3)
Z = 5 + j3,76 Ом или 6,26 Ом при фазовом угле -37,016
Ток, протекающий по цепи, равен
I = V/Z = 10/(5+ j3,76) = 1,597 А при фазовом угле -37,016
Для расчета параметров сети для подключения нагревателей вы можете воспользоваться данными в данной статье основными формулами, или же просто позвоните нашим специалистам компании Термоэлемент по телефону и получите полную бесплатную консультацию и помощь с выбором нужных параметров нагревателей для вашей задачи по нагреву.





