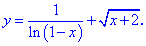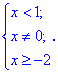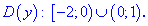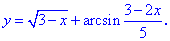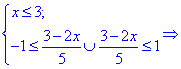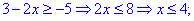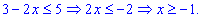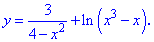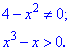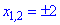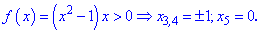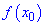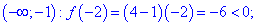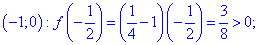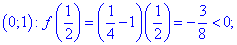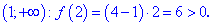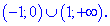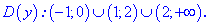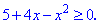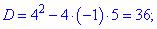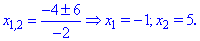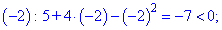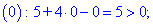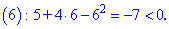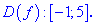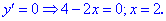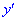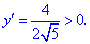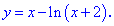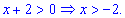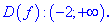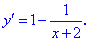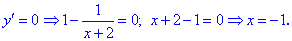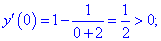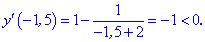Как найти монотонные промежутки - Avtoru.top - решение различных проблем

Тема курса Применение
производной при исследовании и построении графиков функций

Тема
урока №22. Возрастание и убывание функций.
Экстремум функций

Возрастание и убывание функции.

Экстремум функций

Возрастание и убывание функции.

Приведем
формулировки теорем, используемых при исследовании функций.

Достаточное условие строгого
возрастания (убывания) функции.

Если () в интервале , то строго
возрастает (убывает) в этом интервале.

Промежутки, в которых функция возрастает (убывает),
называются промежутками монотонности функции. Чтобы найти промежутки
монотонности функции необходимо:

1. найти область определения функции;

2. найти производную функции;

3. приравнять производную к нулю и определить ее корни
(стационарные точки), а также найти точки, в которых производная не
существует, а функция определена;

4. определить знак производной в каждом из
промежутков, на которые разбивается полученными точками область определения
функции.

Экстремумы функций.

Внутренняя точка интервала называется
точкой максимума (минимума) функции , если существует такое ,
что для всех из интервала , содержащегося внутри интервала , выполняется
неравенство (). Точки максимума и минимума называют точками экстремума
(локального экстремума) функции. Точки, в которых производная обращается в
ноль, называют стационарными точками.

Необходимое условие экстремума
функции

Если функция дифференцируема в
точке и достигает в этой точке максимума (минимума), то .

Точками экстремума могут быть
только те точки, в которых производная равна нулю, либо не существует. Точки, в
которых производная равна нулю или не существует, называют точками,
подозрительными на экстремум, или критическими точками.

Достаточные условия экстремума
функции

Если при переходе через точку ,
подозрительную на экстремум, производная меняет знак, то точка является точкой
экстремума. При этом если в некоторой окрестности точки для и для , то является
точкой максимума. Если же в этой окрестности для и для , то – точка
минимума.

Другим достаточным признаком существования экстремума в
стационарной точке является условие (тогда это точка максимума) и (тогда это
точка минимума). При этом считается, что имеет непрерывную вторую производную
в некоторой окрестности точки .

Примеры. Исследовать функции на минимум и максимум.

. Область определения
функции D(y)=R.

Найдем производную заданной функции

Определим критические точки . Производная не существует при х₂=
0. Следовательно, критические точки: 0 и 2/5. Нанесем их на числовую ось и
определим знак производной на каждом из полученных промежутков.

Критическая точка функции x =3. Точка x= –1
не входит в область определения функции.

Преподаватель: Г.Б.Слямова

Источник

Исследование функций должно начинаться с установления области определения и интервалов монотонности. Для этого студент должен обладать хорошими знаниями поведения элементарных функций и последующим теоретическим материалом.

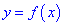
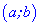
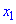
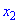
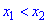
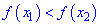
Функция называется возрастающей на интервале если для любых двух точек и с этого промежутка и таких, что выполняется неравенство

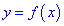
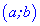
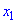
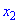
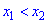
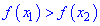
Для того чтобы функция была убывающей на интервале необходимо, чтобы для любых и , принадлежащих к этому интервалу и удовлетворяющих условию исполнялось неравенство
.

Как возрастающие, так и убывающие функции называются монотонными, а интервалы в которых

функция возрастает или убывает – интервалами монотонности.

Область возрастания и убывания функции 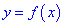характеризуется знаком ее производной: если в

некотором интервале производная больше нуля 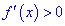, то функция возрастает в этом интервале;

если же наоборот 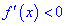– то функция убывает в этом интервале.

Интервалы монотонности могут прилегать друг к другу или точками, где производная равна нулю

или точками, где производная не существует. Эти точки называются критическими точками.

Для того, чтобы найти интервалы монотонности функции 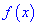нужно:

1) найти область определения функции ;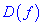

2) вычислить производную данной функции;

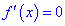
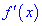
3) найти критические точки из условия равенства нулю производной или при условии, что производная не существует;

4) разделить критическими точками область определения на интервалы, в каждом из которых определить знак производной.

На интервалах где производная положительная функция возрастает, а где отрицательная — убывает.

————————————

Примеры.

Рассмотрим задачу из сборника В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах» на нахождение интервалов монотонности функции.

1. (3.36.10)

Функция существует во всех точках где определен логарифм и он не обращается в нуль, а также где функция под корнем принимает неотрицательные значения. На основе этого находим

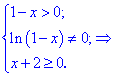
Итак, областью определения будут два интервала

2. (3.36.11)

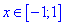
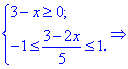
С подкоренной функцией ведем себя как и в предыдущем примере, а функция определена на промежутке . Находим область определения

Единственным промежутком, который удовлетворяет эти условия являются следующий

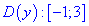
3. (3.36.13)

Область определения функции находим из двух условий

Первое условие дает две точки

в которых функция не существует.

С второго условия получим

Исследуем поведение функции в интервалах монотонности на которые разбивают заданные точки. Для этого

выбираем произвольные точки 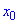из интервалов и проверяем знак

Функция 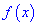принимает положительные значения в интервалах

Вместе с первым условием получим следующую область определения

——————————

Рассмотрим примеры исследования монотонности функции из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика» .

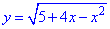
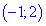
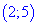
І. (5.705) Показать, что функция возрастает на интервале и убывает в интервале .

1) Областью определения функции будет множество значений для которых подкоренная функция принимает неотрицательные значения.

Решим квадратное уравнение

Определим знак функции на всем интервале

Таким образом получим следующую область определения

2) Найдем производную

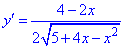
3) Приравняем ее к нулю и найдем критические точки:

Не стоит забывать и о точках, в которых производная не существует. Это корни уравнения в
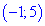
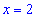
знаменателе. Итак производная существует на интервале в точке меняет знак.

4) Знаки производной: подставляем 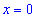в производную

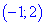
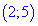
Так что на интервале функция возрастает, а на — убывает.

ІІ. (5.715) Найти интервалы монотонности функции

1. Областью определения будет множество точек для которых существует логарифм функция. На

основе этого получим

Итак

2) Найдем производную функции

3) Находим критические точки

Другая точка, где производная не существует это 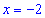, не принадлежит области определения функции.

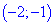
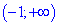
Таким образом получили два интервала монотонности и .

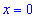
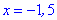
4) Выясним где функция возрастает, а где убывает. Подставим точки и в выражение для

производной

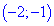
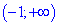
Исследуемая функция на интервале убывает и на растет.

При исследовании функций на монотонность определите все критические точки в которых производная равна нулю или не существует. Также не забывайте при этом учитывать область определения функции. Остальное зависит от Ваших знаний свойств элементарных функции, поскольку именно на их основе построены все задачи, которые Вам задают преподаватели.

———————————————-

Посмотреть материалы:

Исследования функции и построения графика
Наибольшее и наименьшее значение функции на отрезке
Локальный экстремум функции. Примеры
Выпуклость и вогнутисть графика функции
Асимптоты функции
Область определения функции

Источник

Как определить промежутки монотонности

Интервалом монотонности функции можно назвать промежуток, в котором функция либо только возрастает, либо только убывает. Ряд определенных действий поможет найти такие диапазоны для функции, что нередко требуется в алгебраических задачах подобного рода.

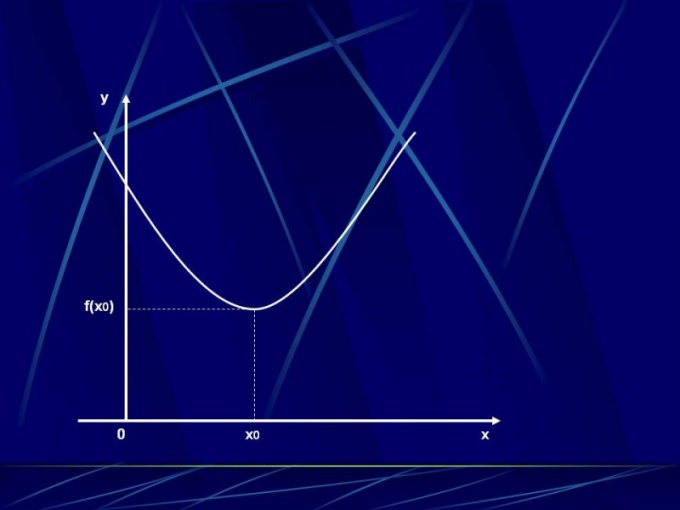
Инструкция

Первым шагом в решении задачи по определению интервалов, в которых функция монотонно возрастает или убывает, станет вычисление области определения данной функции. Для этого узнайте все значения аргументов (значения по оси абсцисс), для которых можно найти значение функции. Отметьте точки, в которых наблюдаются разрывы. Найдите производную функции. Определив выражение, которое представляет собой производную, приравняйте его к нулю. После этого следует найти корни получившегося уравнения. Не забывайте про область допустимых значений.

Точки, в которых функция не существует либо в которых ее производная равна нулю, представляют собой границы интервалов монотонности. Эти диапазоны, а также точки, их разделяющие, следует последовательно внести в таблицу. Найдите знак производной функции в полученных промежутках. Для этого подставьте в выражение, соответствующее производной, любой аргумент из интервала. Если результат положительный, функция в данном диапазоне возрастает, в обратном случае — убывает. Результаты вносятся в таблицу.

В строку, обозначающую производную функции f’(x), записывается соответствующий значениям аргументов символ: «+» — если производная положительна,«-» — отрицательна или «0» – равна нулю. В следующей строке отметьте монотонность самого исходного выражения. Стрелка вверх соответствует возрастанию, стрелка вниз – убыванию. Отметьте точки экстремума функции. Это точки, в которых производная равна нулю. Экстремум может быть либо точкой максимума, либо точкой минимума. Если предыдущий участок функции возрастал, а текущий убывает, значит это точка максимума. В случае, когда до данной точки функция убывала, а теперь возрастает – это точка минимума. Внесите в таблицу значения функции в точках экстремума.

Источники:

что такое определение монотонность

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

1.Если производная функции y
= f(x)
положительна (отрицательна) во всех
точках промежутка, то функцияy
= f(x)
монотонно возрастает (убывает)на этом промежутке.

2.Точкаx₀называется точкоймаксимума (минимума)
функцииy = f(x),
если существует интервал, содержащий
точкуx₀, такой,
что для всехxиз этого
интервала имеет место неравенствоf(x₀)≥ f(x),(f(x₀)≤ f(x)).
Точки максимума и точки минимума
называются точкамиэкстремума.

3. Необходимое условие экстремума:
в точке экстремума функции ее производная
либо равна нулю(f
′(x)=0), либо
не существует.

4.Первое достаточное условие
экстремума: если в точке x₀функцияy = f(x)
непрерывна, а производная f
′(x)при
переходе через точкуx₀меняет знак, то точкаx₀– точка экстремума: максимума, если
знак меняется с «+» на «-», и минимума,
если с «–» на «+».

Если при переходе через точку x₀производная не меняет знак, то в точкеx₀экстремума нет.

5.Второе достаточное условие
экстремума: если в точкеx₀
,
а
,
тоx₀является точкой
максимума функции. Если
,
а
,
тоx₀является точкой
минимума функции.

6.Схема исследования функции

на экстремум:

1) найти производную
;

2) найти критические точки функции, в
которых производная равна нулю или не
существует;

3) исследовать знак производной слева
и справа от каждой критической точки и
сделать вывод о наличии экстремумов
функции;

4) найти экстремальные значения функции.

При исследовании функции на экстремум
с помощью 2-го достаточного условия п.
1), 2), 4) сохраняются, а в п. 3) необходимо
найти вторую производную
и определить ее знак в каждой критической
точке.

7.Чтобы найтинаибольшее и наименьшее
значение(глобальный максимум и
минимум) функции
на отрезке [a,b]
следует выбрать наибольшее (наименьшее)
из значений функции в критических
точках, находящихся в интервале (a,b)
и на концах отрезка (в точкахaиb).

8.Если дифференцируемая на интервале
(a,b) функция
имеетединственнуюточку экстремума,
то в этой точке достигается наибольшее
или наименьшее значение (глобальный
максимум или минимум) функции на интервале
(a,b).

8.35. Найти интервалы монотонности
и экстремумы функции.

Решение. В соответствии со схемой
исследования (п. 6) найдем
.Очевидно, производная существует при
всех значенияхx. Приравниваяy′ к нулю, получаем
уравнение

откудаи— критические точки. Знаки производной
имеют вид (рис. 8.1):

Рис. 8.1

На интервалах
ипроизводная
и функция возрастает, на интервалеи функция убывает;

Рис. 8.2

— точка максимума и— точка минимума и,
так как при переходе через эти точки
производная меняет свой знак соответственно
с «+» на «-» и с «-» на «+».

Замечание.Установить
существование экстремума в критических
точкахи,
в которых
можно было и с помощью второй производной
(см.
п. 5). Так как
,
а
,
то— точка максимума, а— точка минимума.

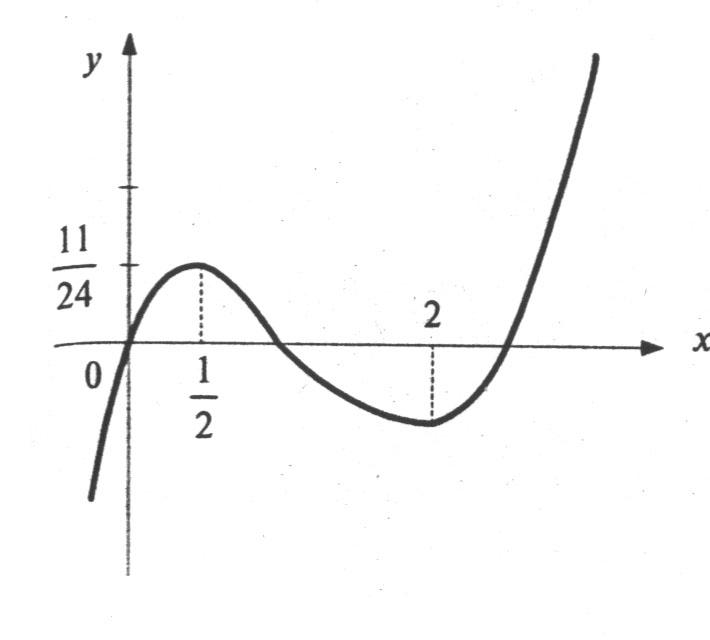
График данной функции схематично показан
на рисунке 8.2.

8.36. Найти экстремумы и интервалы
монотонности функции.

Решение..

Производная существует во всех точках,
в которых существует и сама функция,
т.е. при x> 0. Точки, в
которых производная обращается в нуль,
задаются равенствамиlnx=0,lnx-1
= 0, откудаx₁=1,x₂= е – критические точки. Знаки
производной указаны на рис. 8.3.

Рис.8.3

Таким образом, функция монотонно
возрастает на промежутках (0;1) и (е;+)
и монотонно убывает на промежутке (1;е).
Точкаx= 1 – точка максимума
и,
точка х = е – точка минимума и.

8.37. Найти экстремумы и интервалы
монотонности функции

Решение..
Производная не существует приcosx=1 т.е. прии равна нулю при.
Знак производной совпадает со знакомsin(x); таким
образом у’ >0 прииy'<0 при.
Это, соответственно, интервалы возрастания
и убывания функции.— точки максимума,— точки минимума.

8.38. Найти наибольшее значение
(глобальный максимум) функциина интервале (10;18).

Решение. Найдем.
На интервале (10;18) имеется всего одна
критическая точкаx= 6.
Производная при переходе через эту
точку меняет знак с «+» на «-», т.е.x= 6 – точка максимума. Следовательно,
функция достигает наибольшего значения
приx= 16, т.е..
(Заметим, что наименьшего значения
(глобального минимума) данной функции
на указанном интервале не существует.)

8.40. Забором длиной 24 метра требуется
огородить с трех сторон прямоугольный
палисадник наибольшей площади. Найти
размеры палисадника.

Решение.Пусть длины сторон палисадникаx,y. Тогда
2x+y= 24, т.е.y= 24-2x.
Площадь палисадникаS=xy=x(24-2x)
= 24x-2x²,
где 0<x<12 (ибо 24-2x>0).
Таким образом, задача свелась к отысканию
значенияx, при которомS(x) принимает
наибольшее значение на интервале (0;12).
НайдемS'(x)
= 24-4x= 0 приx= 6. Легко видеть, чтоx= 6
– единственная точка экстремума –
максимума функцииS(x).
Это означает, что на интервале (0;12)S(x)
принимает наибольшее значение приx= 6, т.е. искомые размеры палисадника 6 м
и 24- 2 — 6 = 12 м.

Найти интервалы
монотонности и экстремумы функции:

8.41..8.42..8.43..

8.44.
.8.45.
8.46.
.

8.47.
.8.48..8.49..

8.50..8.51..8.52.
.

8.53.
.8.54.
.8.55.
.

8.56..8.57.
.8.58.
.

8.59..8.60..

Найти наибольшее
и наименьшее значение (глобальный
максимум и минимум) функции
на отрезке [a,b]:

8.61.8.62.8.63.

8.64.8.65.8.66.

8.67.8.68.

Найти наибольшее
или наименьшее значение (глобальный
максимум или минимум) функции
на интервале(a,b):

8.69.8.70.8.71.

8.72.8.73.8.74.

8.75. Рассматриваются всевозможные
прямоугольные параллелепипеды, основания
которых являются квадратами, а каждая
из боковых сторон имеет периметр, равный
6 см. найти среди них параллелепипед с
наибольшим объемом и найти этот объем.

8.76. Определить размеры открытого
бассейна с квадратным дном, при которых
на облицовку стен и дна пойдет наименьшее
количество материала. Объем бассейнаVфиксирован.

8.77. Требуется огородить два участка:
один в форме правильного треугольника,
другой в форме полукруга. Длина изгороди
фиксирована и равна Р. Определить размеры
участков (сторону треугольника и радиус
полукруга) так, чтобы сумма площадей
этих участков была бы наименьшей.

8.78. В треугольнике с основаниемaи высотойh вписан
прямоугольник, основание которого лежит
на основании треугольника, а две вершины
— на боковых сторонах. Найти наибольшую
площадь вписанного прямоугольника.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Найти интервалы монотонности функции

Онлайн калькулятор поможет найти промежутки монотонности функции. Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает.

Например для исследования функции f(x) на монотонность необходимо:
Найти f(x).
Найти нули производной.
На числовой оси отметить область определения f(x), нули производной и те точки, где производная не существует.
На каждом из полученных интервалов определить знак производной f(x) .
Сделать вывод о возрастании или убывании функции на каждом интервале.
Интервалы возрастания функции при: >0
Интервалы убывания функции при: <0

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция «И» ∧: &&
дизъюнкция «ИЛИ» ∨: ||
отрицание «НЕ» ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo