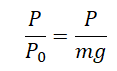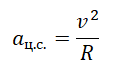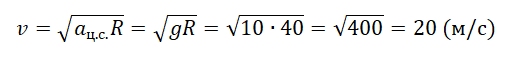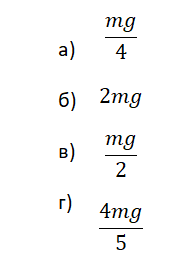Как найти момент веса - Avtoru.top - решение различных проблем

Рассмотрим примеры того, как можно на практике применить условия равновесия твердого тела.

Пример 1. Равноплечие весы

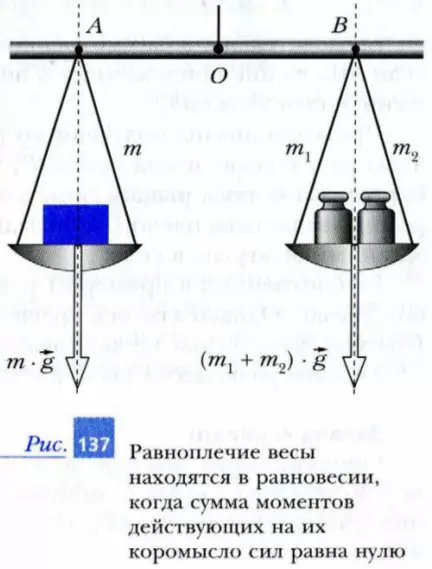
Еще с древнейших времен для определения массы тел люди использовали равноплечие весы (рис. 137). Понять принцип их работы просто, если воспользоваться вторым условием равновесия твердого тела.

Коромысло весов может поворачиваться вокруг оси, проходящей через точку O. На равных расстояниях от оси вращения коромысла подвешены одинаковые чашки. В одну чашку помещают груз неизвестной массы m, а в другую – набор грузов известной массы, например m₁ + m₂. Весы будут находиться в равновесии, если стремящиеся развернуть их коромысло положительный момент m · g · OA и отрицательный момент -(m₁ + m₂) · g · OB будут уравновешивать друг друга. Поэтому условие равновесия коромысла весов можно записать в виде:

m · g · OA — (m₁ + m₂) · g · OB = 0

Так как плечо OA силы тяжести груза равно плечу OB силы тяжести гирь, то уравнение обратится в тождество при условии, что m = m₁ + m₂. Таким образом, равноплечие весы будут находиться в равновесии, если суммарная масса гирь будет равна массе взвешиваемого груза.

Если массы груза и гирь не равны друг другу, то коромысло весов начнет разворачиваться в сторону большего по модулю момента силы тяжести (в сторону большей массы). Чашка весов с большей массой начнет опускаться. Добавляя (или уменьшая) число гирь известной массы, можно достичь равновесия и таким образом измерить неизвестную массу груза.

Пример 2. Рычаг

Рычагом называют твердое тело, способное вращаться вокруг неподвижной оси (или опоры). Применение рычага позволяет получить выигрыш в силе – преодолеть действие большей силы, приложив меньшую силу. Каким образом это можно сделать?

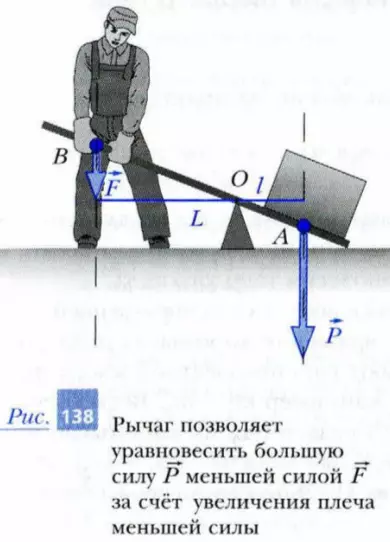
Рассмотрим человека, поднимающего камень весом P с помощью рычага (рис. 138). Человек действует на противоположный конец рычага силой F, направленной вертикально вниз. Под действием моментов сил F и P рычаг может вращаться вокруг оси O. Обозначим плечо силы F символом L, а плечо силы P – символом l. Рычаг будет находиться в равновесии, если сумма вращающих его моментов сил будет равна нулю:

F · L — P · l = 0 или F/P = l/L

Следовательно, в рассмотренном случае рычаг находится в равновесии, если отношение приложенных к нему сил обратно пропорционально отношению плеч этих сил.

Проведем анализ полученного результата. Если плечо L силы F будет в два раза больше плеча l силы P, то для поднятия камня человек должен будет приложить к рычагу силу, в два раза меньшую веса камня. Таким образом, увеличивая плечо L прикладываемой силы, можно получить заранее заданный выигрыш в силе.

Рассмотренные в примере 1 равноплечие весы также представляют собой рычаг. Однако его ось вращения совпадает с серединой коромысла. Поэтому такой рычаг не дает выигрыша в силе.
Условие равновесия рычага можно использовать для решения задач.

Задача «качели»

Старший брат массой M = 60 кг посадил младшего брата массой m = 40 кг на легкую доску качелей на расстоянии L = 3 м от оси ее вращения (рис. 139). Куда должен сесть старший брат, чтобы доска находилась в равновесии?

Решение. Ясно, что старший брат должен сесть с противоположной стороны на таком расстоянии l от оси вращения, чтобы выполнялось условие равновесия доски качелей относительно этой оси: M · g · l — m · g · L = 0.

Следовательно,

l = (m · L) / M = (40 кг · 3 м) / 60 кг = 2 м.

Ответ: чтобы качели находились в равновесии, старший брат должен сесть на расстоянии 2 м от оси вращения качелей.

Найдите силу, с которой доска качелей при этом будет действовать на ось вращения (опору). Массой доски качелей можно пренебречь.

Решение. По третьему закону Ньютона искомая сила F, с которой доска качелей действует на ось вращения (опору), равна по модулю силе N реакции опоры, с которой ось вращения действует на доску. Для того чтобы найти силу N реакции опоры, применим к доске первое условие равновесия твердого тела. На доску действуют три силы (со стороны двух братьев и со стороны оси вращения). Если ось системы отсчета, связанной с Землей, направить вертикально вверх, то первое условие равновесия твердого тела для доски примет вид: N — M · g — m · g = 0. Следовательно, искомая сила направлена вертикально вниз, а ее модуль равен

F = N = (M + m) · g = 1000 Н = 1 кН.

Ответ: модуль силы, с которой доска качелей действует на опору, равен 1 кН.

Мы рассмотрели рычаги, в которых ось вращения находится между точками приложения действующих сил. На практике используют также рычаги, у которых точки приложения сил находятся по одну сторону от оси вращения. Такие рычаги часто называют рычагами второго рода. На рис. 140 изображен подобный рычаг.

Задача «рычаг второго рода»

На каком расстоянии L от точки опоры O (см. рис. 140) должен взяться за легкий рычаг рабочий, чтобы приподнять груз массой M = 200 кг? Линия действия веса этого груза проходит на расстоянии l = 60 см от точки опоры. Рабочий прикладывает к рычагу силу, направленную вертикально вверх, ее модуль F = 600 Н.

Решение. На рычаг действуют вес груза P = M · g и сила F со стороны рабочего. При этом относительно оси вращения (точки опоры O) момент веса груза положителен, а момент силы, приложенной рабочим, отрицателен. Поэтому условие равновесия данного рычага имеет вид:

M · g · l — F · L = 0.

Следовательно, L = (M · g · l) / F = (200 кг ·10 м/с² · 0,6 м) / 600 Н = 2 м.

Ответ: рабочий должен взяться за рычаг на расстоянии L = 2 м от точки опоры.

Итоги

Рычагом называют твердое тело, способное вращаться вокруг неподвижной оси (или опоры).

Рычаг дает выигрыш в силе, равный отношению плеч сил. При этом отношение модулей приложенных к нему сил обратно пропорционально отношению плеч этих сил.

Вопросы

Что называют рычагом? Приведите примеры рычагов в быту и в технике.
Сформулируйте условие равновесия рычага.
Как с помощью рычага получить выигрыш в силе?
Чем отличается рычаг первого рода от рычага второго рода?
Предложите способы определения равноплечности весов.

Упражнения

Определите массу камня, который приподнимает человек (рис. 138), прикладывая силу F, модуль которой равен 800 Н. Расстояние OB = 3 м, OA = 40 см. Массой рычага пренебречь.
Соберите группу из пяти человек. Узнайте свои массы и рассчитайте расстояния от точки опоры доски качелей, на которые каждому из вас необходимо сесть, чтобы качели с пятью учащимися находились в равновесии (сделайте рисунок, на котором изобразите действующие на доску силы и их плечи). Для проверки полученного ответа проведите эксперимент с качелями (используйте рулетку).
Как с помощью неравноплечих весов и набора гирь определить неизвестную массу груза?
В каком случае палка сильнее давит на плечо путника, показанного на рис. 141, а и б? (Подсказка: определите, рычагом какого рода является палка.)
Допустим, вам нужно поднять груз массой 100 кг, а вы можете приложить в вертикальном направлении силу не более 200 Н. Какой рычаг второго рода потребуется вам для выполнения задачи? Нарисуйте схему эксперимента, указав на ней силы и их плечи.

Источник

Сила тяжести. Вес

Движение тел вблизи поверхности Земли
Сила тяжести
Вес тела
Невесомость
Задачи
Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести

п.1. Движение тел вблизи поверхности Земли

Вблизи поверхности Земли все тела, предоставленные самим себе, падают вниз, независимо от направления начальной скорости.

Такое движение тел называют свободным падением.

п.2. Сила тяжести

Многочисленные эксперименты показали, что в свободном падении все тела вблизи поверхности Земли падают с одинаковым ускорением (overrightarrow{g}), которое направлено вниз, к центру Земли.

В системе отсчета, связанной с Землей, на любое тело массой (m) действует сила тяжести $$ overrightarrow{F_{text{тяж}}}=m overrightarrow{g} $$

Сила тяжести прямо пропорциональна массе тела.
Точка приложения силы тяжести – центр масс тела.
Сила тяжести всегда направлена вертикально вниз, к центру Земли.

Измерения показывают, что на средних географических широтах ускорение свободного падения (gapprox 9,81 text{м/с}^2). Т.е., скорость при падении увеличивается на (9,81 text{м/с}) каждую следующую секунду.

В общем случае, ускорение свободного падения зависит от широты рассматриваемого места, высоты над уровнем моря, времени суток и ещё нескольких более «тонких» факторов.
Самое низкое значение (g_{min}approx 9,7639 text{м/с}^2) зарегистрировано в Перу, на горе Уаскаран (1000 км южнее экватора).
Самое высокое значение (g_{max}approx 9,8337 text{м/с}^2) получено в 100 км от северного полюса.

В школьных задачах, если другое не оговорено, для вычислений используют приблизительное значение (gapprox 10 text{м/с}^2).
Стандартное значение, используемое для лабораторных измерений и расчетов, равно (g=9,80665 text{м/с}^2).

п.3. Вес тела

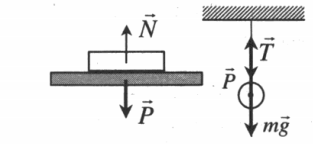
Если подвесить тело или положить его на опору, сила тяжести, действующая на тело, будет уравновешена силой, которую называют силой реакции подвеса или силой реакции опоры.

Т.к. силы уравновешивают друг друга, выполняется соотношение $$ moverrightarrow{g}=-overrightarrow{N} $$ где (moverrightarrow{g}) — сила тяжести, (overrightarrow{N}) — реакция подвеса или опоры.

По третьему закону Ньютона, если подвес или опора действуют на тело с силой (overrightarrow{N}), то и тело действует на подвес или опору с силой (overrightarrow{P}=-overrightarrow{N})

Вес тела – это сила, с которой тело действует на подвес или опору.

Получаем, что (overrightarrow{P}=moverrightarrow{g}), вес и сила тяжести равны по величине и направлению, но приложены к разным точкам: сила тяжести – к центру масс тела, вес – к подвесу или опоре.

По своей природе реакции подвеса или опоры являются силами упругости: под действием веса тела подвес или опора деформируются, и силы упругости стремятся восстановить их форму и размеры.

Равенство (overrightarrow{P}=moverrightarrow{g}) выполняется, если подвес или опора покоятся или движутся относительно Земли прямолинейно и равномерно.

Если движение подвеса или опоры равноускоренное с ускорением (overrightarrow{a}ne 0), то (overrightarrow{P}ne moverrightarrow{g}), вес будет больше (при (overrightarrow{a}) направленном вверх) или меньше (при (overrightarrow{a}) направленном вниз) силы тяжести. Подробней этот случай будет рассмотрен в курсе физики для 9 класса.

п.4. Невесомость

Если опора свободно падает вместе с телом, то под действием силы тяжести каждая частица опоры и тела двигается вниз с одним и тем же ускорением (overrightarrow{g}). Ни в опоре, ни в теле не возникают сжатия или растяжения, нет сил упругости, а значит, вес тела равен нулю.

Состояние, при котором в свободно падающих телах исчезают деформации и взаимные давления частиц тел друг на друга, называют невесомостью.

Состояние невесомости можно испытать, если подпрыгнуть – с момента отрыва от земли до момента приземления. В первые моменты прыжка до раскрытия парашюта, парашютисты также находятся в состоянии невесомости.

Движение космического корабля по орбите вокруг Земли представляет собой непрерывное свободное падение, поэтому космонавты испытывают состояние невесомости в течение всего полета, кроме тех моментов, когда передвигаются по кораблю или включают двигатели для маневрирования.

п.5. Задачи

Задача 1. Какой вес имеет человек массой 65 кг, который стоит на земле?

Дано:
(m=65 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(P-?)

Вес равен силе тяжести (P=mg) $$ Papprox 65cdot 10=650 (text{Н}) $$ Ответ: 650 Н

Задача 2. Парашютист равномерно опускается на землю. Сила сопротивления воздуха 900 Н. Масса парашюта 15 кг. Найдите массу парашютиста.

Дано:
(F_{text{сопр}}=900 text{Н})
(m_1=15 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)

На раскрытый парашют действуют две силы: сила сопротивления воздуха, направленная вверх, и суммарный вес (парашюта и парашютиста), направленный вниз.
Т.к. движение равномерное, ускорение (a=0). Значит, вес равен силе тяжести, и begin{gather*} F_{text{сопр}}=P=F_{text{т}}=(m_1+m_2)g\[6pt] m_1+m_2=frac{F_{text{сопр}}}{g}Rightarrow m_2=frac{F_{text{сопр}}}{g}-m_1 end{gather*} Подставляем $$ m_2=frac{900}{10}-15=75 (text{кг}) $$ Ответ: 75 кг.

Задача 3. На сколько сантиметров растянется пружина жесткостью k=267 Н/м, если подвесить к ней медный брусок размерами 5 см х 6 см х 10 см. Плотность меди 8900 кг/м³.

Дано:
(V=5 text{см}times 6 text{см}times 10 text{см}=300 text{см}^3=3cdot 10^{-4} text{м}^3)
(rho=8900 text{кг/м}^3)
(k=1000 text{Н/м})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)

Вес бруска равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow Delta l=frac{mg}{k}, m=rho V\[6pt] Delta l=frac{rho Vg}{k} end{gather*} Получаем: $$ Delta l=frac{8900cdot 3cdot 10^{-4}cdot 10}{267}=0,1 (text{м}=10 (text{см}) $$ Ответ: 10 см.

Задача 4*. При подвешивании гирьки массой 450 г пружина динамометра растягивается до 8 см. А при подвешивании гирьки массой 300 г – до 6 см. Найдите длину пружины динамометра без груза (ответ запишите в см).

Дано:
(m_1=450 text{г}=0,45 text{кг})
(l_1=8 text{см}=0,8 text{м})
(m_2=300 text{г}=0,3 text{кг})
(l_2=6 text{см}=0,6 text{м})
__________________
(l_0-?)

Вес гирьки равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow k=frac{mg}{Delta l} end{gather*} где (Delta l=l-l_0) – растяжение пружины.
Жесткость пружины begin{gather*} k=frac{m_1g}{Delta l_1}=frac{m_1g}{l_1-l_0}, k=frac{m_2g}{Delta l_2}=frac{m_2g}{l_2-l_0}\[6pt] frac{m_1g}{l_1-l_0}=frac{m_2g}{l_2-l_0} Rightarrow frac{m_1}{l_1-l_0}=frac{m_2}{l_2-l_0} Rightarrow m_2(l_2-l_0)=m_2(l_1-l_0)\[6pt] m_1l_2-m_1l_0=m_2l_1-m_2l_0 Rightarrow m_1l_2-m_2l_1=(m_1-m_2)l_0\[6pt] l_0=frac{m_1l_2-m_2l_1}{m_1-m_2} end{gather*} Получаем $$ l_0=frac{0,45cdot 0,06-0,3cdot 0,08}{0,45-0,3}=frac{0,027-0,024}{0,15}=0,02 (text{м}=2 (text{см}) $$ Ответ: 2 см.

п.6. Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести

Цель работы
Исследовать зависимость силы упругости от величины деформации. Изготовить шкалу динамометра. Измерить силу тяжести для двух тел неизвестной массы; рассчитать их массу.

Теоретические сведения

При подвешивании груза на пружину, его вес уравновешивается силой упругости. Для неподвижной пружины вес равен силе тяжести.
Получаем $$ P=F_{text{т}}=mg=F_{text{упр}} =kDelta l $$ Удлинение пружины $$ Delta l=frac gk m $$ При постоянном ускорении свободного падения (g) и постоянной жесткости (k), удлинение прямо пропорционально массе подвешенного груза.

В данной работе считаем, что грузу массой 100 г соответствует показание динамометра (F=1 text{Н}), т.е. (overline{g}=frac{1 text{Н}}{100 text{г}}=10frac{text{Н}}{ text{кг}}=10frac{ text{м}}{ text{с}^2}). Более точное стандартное значение (g_0=9,80665frac{ text{м}}{ text{с}^2})

Ошибка метода, связанная с величиной (g) $$ delta_g=frac{|overline{g}-g_0|}{g_0}approx 0,02=2text{%} $$ Тогда грузу массой 200 г соответствует показание 2 Н, 300 г – 3 Н и т.д.

После градуирования в целых значениях Н на динамометре наносятся промежуточные деления с ценой деления (d=0,1 text{Н}).

Ошибка градуирования определяется как степень отклонения от равномерности шкалы, (delta_{text{шк}}).

Теперь с помощью полученного прибора можно непосредственно измерять силу тяжести, действующую на тела. Ошибка метода при определении сил равна сумме (delta=delta_g+delta_{text{шк}}).

Т.к. шкала изготовлена для (overline{g}=10frac{ text{м}}{ text{с}^2}), массу тел находим по формуле (m=frac{F}{overline{g}}), где (F) — показание динамометра. При этом ошибка метода равна (delta=delta_{text{шк}}), т.к. ошибка (delta_g) нивелируется за счет пропорциональности массы и растяжения пружины.

Таким образом, за счет сокращения (overline{g}), полученный прибор позволяет точнее измерять массы по сравнению с измерениями сил.

Приборы и материалы
Лабораторный динамометр на 5Н со шкалой, закрытой чистой бумагой; набор грузиков по 100 г; линейка; карандаш; 2 тела неизвестной массы.

Ход работы
1. Закрепите динамометр в штативе.
2. Подвесьте грузик массой 100 г, сделайте отметку 1Н на шкале.
3. Сделайте отметки 2Н, 3Н, 4Н и 5Н для грузов 200 г, 300 г, 400 г и 500 г соответственно.
4. Снимите динамометр со штатива и проверьте с помощью линейки, насколько равномерной получилась шкала. Оцените относительную ошибку (delta_{text{шк}})
5. С помощью линейки нанесите по 10 промежуточных делений между основными делениями шкалы.
6. Снова закрепите динамометр в штативе и проведите измерения силы тяжести для двух тел неизвестной массы. Найдите абсолютную и относительную погрешность измерений.
7. Рассчитайте массы для обоих тел. Найдите абсолютную и относительную погрешность расчетов. 8. Сделайте выводы.

Результаты измерений и вычислений

Расчетная таблица для оценки равномерности шкалы

Отрезок шкалы	Длина отрезка, мм	(\|x-x_{text{ср}}\|)
0-1 Н	25	0
1-2 Н	25	0
2-3 Н	26	1
3-4 Н	24	1
4-5 Н	25	0
Всего	125	2

Средняя длина отрезка $$ x_{text{ср}}=frac{125}{5}=25 (text{мм}) $$ Среднее линейное отклонение $$ Delta =frac 25=0,4 (text{мм}) $$ Цена деления линейки (d_{text{л}}=1 text{мм}), абсолютная погрешность измерений (Delta_{text{л}}=0,5 text{мм})
Т.к. (Delta_{text{л}}gt Delta), принимаем погрешность равномерности шкалы (Delta=Delta_{text{л}}=0,5 text{мм})
Относительная погрешность равномерности шкалы $$ delta_{text{шк}}=frac{0,5}{25}=0,02=2text{%} $$

Относительная погрешность равномерности шкалы

	Показание динамометра (F, text{Н})	Ошибка метода (delta=delta_g+delta_{text{шк}}, text{%})	Абсолютная погрешность (Delta F=deltacdot F, text{Н})
1-е тело	2,7	4%	0,11 ≈ 0,1
2-е тело	1,9	4%	0,08 ≈ 0,1

Цена деления динамометра (d=0,1 text{Н}); погрешность прямых измерений (Delta_0=frac d2=0,05 text{Н})

Полученные абсолютные погрешности больше (Delta_0).

Сила тяжести для первого тела (F_1=(2,7pm 0,1) text{Н}, delta=4text_%)

Сила тяжести для второго тела (F_2=(1,9pm 0,1) text{Н}, delta=4text_%)

Расчет массы $$ m=frac{F}{10} (text{кг})=100F (text{г}) $$

	Масса (m=100F, text{г})	Ошибка метода (delta=delta_{text{шк}}, text{%})	Абсолютная погрешность (Delta m=deltacdot m, text{г})
1-е тело	270	2%	5
2-е тело	190	2%	4

Масса первого тела (m_1=(270pm 5) text{г}, delta=2text{%})

Масса второго тела (m_2=(190pm 4) text{г}, delta=2text{%})

Выводы
На основании проделанной работы можно сделать следующие выводы.

Для градуирования динамометра в ньютонах использовалось значение $$ overline{g}=10 frac{text{м}}{text{с}^2} $$

По сравнению со стандартным значением (g_0=9,80665 text{м/с}^2) это приводит к вкладу в ошибку метода (delta_gapprox 2text{%}).

При градуировании равномерность шкалы дала составляющую ошибки метода (delta_{text{шк}}=2text{%}).

При определении силы тяжести с помощью полученного динамометра ошибка метода равна сумме (delta+delta_g+delta_{text{шк}}=4text{%}).

Для двух тел неизвестной массы были получены следующие значения сил тяжести: $$ F_1=(2,7pm 0,1) text{Н}, F_2=(1,9pm 0,1) text{Н}, delta=4text{%} $$

При расчете массы по формуле (m=frac Fg), ошибка (delta_g) нивелируется за счет пропорциональности растяжения пружины. Ошибка метода уменьшается (delta=delta_{text{шк}}=2text{%}).

Получаем следующие значения масс: $$ m_1=(270pm 5) text{г}, m_2=(190pm 4) text{г}, delta=2text{%} $$ Таким образом, полученный в ходе работы динамометр позволяет измерять силы тяжести в интервале от 0 до 5 Н с погрешностью 4% и рассчитывать массы тел в интервале от 0 до 500 г с погрешностью 2%.

Источник

Загрузить PDF

Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).

1

Для вычисления веса используйте формулу . Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула .^[1]
2

Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с². В других местах Вселенной эта величина меняется.^[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с² (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.^[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с² (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).^[5]
4

Подставьте значения в формулу . Теперь, когда вы знаете массу и ускорение свободного падения , подставьте их значения в формулу . Так вы найдете вес тела (измеряется в ньютонах, Н).

Реклама

1

Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
2

Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
3

Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.

Реклама

1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
2

Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с²), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.

Реклама

Приложение: вес, выраженный в кгс

Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
1 кгс = 9,8166 Н.
Разделите вес, выраженный в ньютонах, на 9,80665.
Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.

Советы

Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с².
Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.

Предупреждения

Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».

Об этой статье

Эту страницу просматривали 113 870 раз.

Была ли эта статья полезной?

Источник

примеры уменьшения веса:

при быстрой езде на велосипеде по небольшим пригоркам велосипедист на вершине пригорка испытывает ощущение лёгкости.

Когда лифт резко начинает движение вниз, находящиеся в лифте люди ощущают, что уменьшается их давление на пол, возникает ощущение свободного падения.

Когда на американских горках проезжают через высшую точку горок, находящиеся в тележке люди испытывают ощущение, будто их «подбрасывает» в воздух.

Когда на качелях раскачиваются до наивысшей точки, ощущается, что на короткий момент тело «зависает» в воздухе.

Изменение веса связано с инерцией — стремлением тела сохранять своё начальное состояние. Поэтому изменение веса всегда противоположно ускорению движения. Когда ускорение движения направлено вверх, вес тела увеличивается. А если ускорение движения направлено вниз, вес тела уменьшается.

Источник

Определение

Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.

Вес тела имеет электромагнитную природу (не путать с силой тяжести – она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).

Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.

Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:

P = T; P = N; P = F_упр.

Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:

P₀ = F_тяж = mg

Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.

Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.

Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:

P = mg = 16,38∙10 = 163,8 (Н)

Перегрузка

Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.

Перегрузка определяется отношением:

Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.

Вес тела в движущейся равноускоренно системе

Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:

Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P₀.
Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P₀.
Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P₀.

Применение законов Ньютона для определения веса тела

Опора или подвес неподвижны
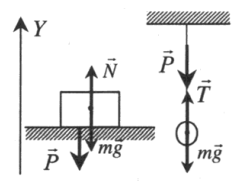	Второй закон Ньютона в векторной форме: N + mg = ma или T + mg = ma Проекция на ось ОУ: N – mg = 0 или T — mg = 0
Ускорение опоры направлено вверх
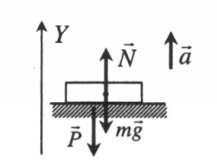	Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ: N – mg = ma Вес тела: P = N = ma + mg = m(a + g)
Ускорение опоры направлено вниз
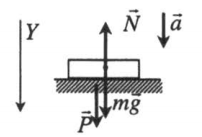	Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ: mg – N = ma Вес тела: P = N = mg – ma = m(g – a)
Вершина выпуклого моста
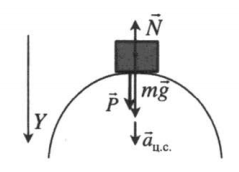	Второй закон Ньютона в векторной форме: N + mg = ma_ц.с. Проекция на ось ОУ: mg – N = m a_ц.с. Вес тела: P = N = mg – m a_ц.с. = m(g – a_ц.с.)
Нижняя точка вогнутого моста
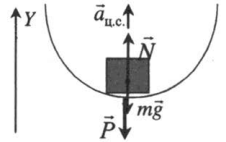	Второй закон Ньютона в векторной форме: N + mg = ma_ц.с. Проекция на ось ОУ: N – mg = ma_ц.с. Вес тела: P = N = ma_ц.с. + mg = m(a_ц.с. + g)
Полный оборот на подвесе
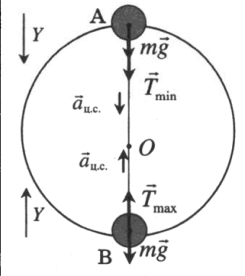	Второй закон Ньютона в векторной форме: T + mg = ma Проекция на ось ОУ в точке А: T + mg = ma_ц.с. Вес тела в точке А: P = T = ma_ц.с. – mg = m (a_ц.с.– g) Проекция на ось ОУ в точке В: T – mg = ma_ц.с. Вес тела в точке В: P = T = ma_ц.с. + mg = m (a_ц.с.+ g) *Важно!* Центростремительное ускорение всегда направлено к центру окружности.

Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?

Вес тела в верхней точке выпуклого моста равен:

P = m(g – a_ц.с.)

Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:

m(g – a_ц.с.) = 0

Масса не может быть нулевой, поэтому:

g – a_ц.с.= 0

g = a_ц.с

Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:

Отсюда скорость автомобиля в верхней точке моста должна быть равна:

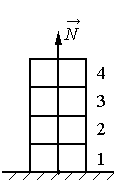
Задание EF18133

Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…

Алгоритм решения

1.Вычислить силу, с которой оставшиеся кирпичи давят на опору.

2.Применить третий закон Ньютона.

3.Определить силу, с которой действует горизонтальная опора на первый кирпич.

Решение

Так как кирпичи покоятся, вес каждого равен:

P = mg

Вес двух кирпичей равен:

2P = 2mg

Опора действует на первый кирпич с такой же силой, с какой на него действует два кирпича, оставшихся после того, как два верхних кирпича убрали.

Следовательно:

N = 2P = 2mg

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17624

Подъёмный кран поднимает груз с постоянным ускорением. На груз со стороны каната действует сила, равная по величине 8⋅10³H. На канат со стороны груза действует сила, которая:

а) 8∙10³ Н

б) меньше 8∙10³ Н

в) больше 8∙10³ Н

г) равна силе тяжести, действующей на груз

Алгоритм решения

1.Сформулировать третий закон Ньютона.

2.Применить закон Ньютона к канату и грузу.

3.На основании закона сделать вывод и определить силу, которая действует на канат со стороны груза.

Решение

Третий закон Ньютона формулируется так:

«Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны».

Математически он записывается так:

F_A = –F_B

Если на груз со стороны каната действует некоторая сила, то и груз действует на канат с этой силой, которая называется весом этого груза, или силой натяжения нити. Следовательно, груз действует на канат с силой 8∙10³ Н.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22586

Мальчик медленно поднимает гирю, действуя на неё с силой 100 Н. Гиря действует на руку мальчика с силой:

а) больше 100 Н, направленной вниз

б) меньше 100 Н, направленной вверх

в) 100 Н, направленной вниз

г) 100 Н, направленной вверх

Алгоритм решения

1.Записать исходные данные.

2.Сделать чертеж, иллюстрирующий ситуацию.

3.Записать второй закон Ньютона в векторной форме.

4.Записать второй закон Ньютона в виде проекций.

5.Вычислить силу, с которой гиря действует на руку мальчика.

Решение

Запишем исходные данные: мальчик поднимает гирю вверх с силой F = 100 Н.

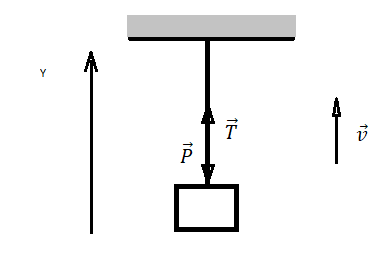
Сделаем рисунок. В данном случае рука мальчика выступает в роли подвеса. Так как мальчик поднимает гирю медленно, можно считать, что он поднимает ее равномерно (равнодействующая всех сил равна нулю). Выберем систему координат, направление оси которой совпадает с направлением движения руки и гири.

На руку (подвес) действуют только две силы. Поэтому второй закон Ньютона выглядит следующим образом:

P + T = 0

Запишем этот же закон в проекции на ось ОУ:

–P + T = 0

Отсюда:

P = T

Следовательно, на руку мальчика действует вес гири, который по модулю равен силе, с которой мальчик действует на эту гирю.

Внимание! Существует второй способ решения задачи через третий закон Ньютона. Согласно ему, тела действуют друг на друга с силами, равными по модулю, но противоположными по направлению.

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 6.6k

Источник

Пример 1. Равноплечие весы

Пример 2. Рычаг

Задача «качели»

Задача «рычаг второго рода»

Сила тяжести. Вес

п.1. Движение тел вблизи поверхности Земли

п.2. Сила тяжести

п.3. Вес тела

п.4. Невесомость

п.5. Задачи

п.6. Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести

Приложение: вес, выраженный в кгс

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

Перегрузка

Применение законов Ньютона для определения веса тела

Опора или подвес неподвижны

Ускорение опоры направлено вверх

Ускорение опоры направлено вниз

Вершина выпуклого моста

Нижняя точка вогнутого моста

Полный оборот на подвесе

Не пропустите также: