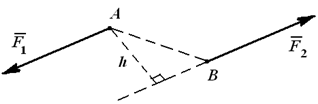
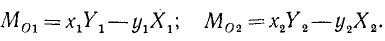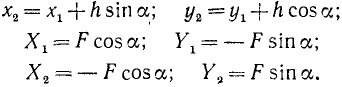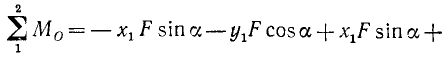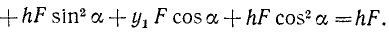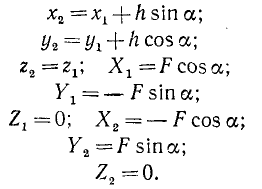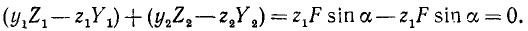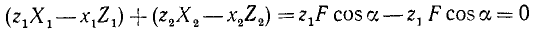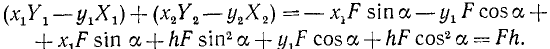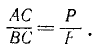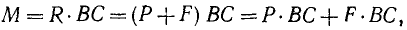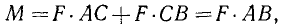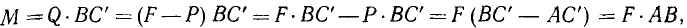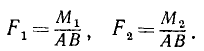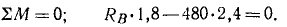Парой сил называется система двух равных по величине, противоположных по направлению и не лежащих на одной прямой сил (рисунок 1.19).
Рисунок 1.19
Пара сил не имеет равнодействующей, т.е. не может быть заменена одной силой.
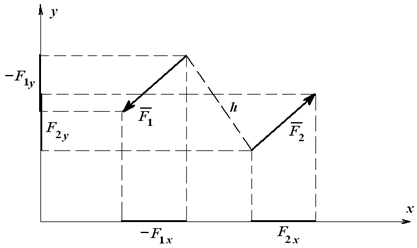
Сумма проекций сил пары на любую ось равна нулю, т.к. их проекции всегда равны и противоположны по знаку (рисунок 1.20).
Рисунок 1.20
Момент пары сил
Пара сил оказывает вращающее действие, которое может быть оценено моментом пары сил:
M(F1, F2) = F1h = F2h, (1.11)
где h – плечо пары.
Короткий видеоурок про момент силы с примерами:
Другие видео
Момент пары считается положительным, если силы пары стремятся повернуть плоскость, в которой они расположены, против хода часовой стрелки (рисунки 1.19, 1.20 – моменты этих пар сил положительны).
Момент пары сил может быть определен как векторная величина:
M(F1, F2) = AB×F2 = BA×F1, (1.12)
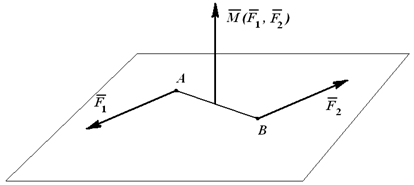
т.е. вектор M(F1, F2) всегда перпендикулярен плоскости, в которой расположена пара сил, и его направление определяется правилом векторного произведения (рисунок 1.21).
В разделе «Статика» дисциплины «Теоретическая механика» доказывается теорема о том, что сумма моментов сил пары относительно произвольной точки пространства равна моменту этой пары. Следовательно, вектор-момент пары сил может быть приложен (или перенесен) к любой точке твердого тела, на которое действует пара сил.
Рисунок 1.21
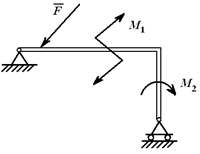
Поскольку действие пары сил оценивается величиной и направлением вращающего момента, то на плоскости пару сил изображают в любом месте твердого тела, задавая величину и направление вращающего действия (см. на рисунке 1.22 изображение пар сил M1 и M2).
Рисунок 1.22
См. также момент силы
Примеры решения задач >
Распределенные нагрузки >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Содержание:
- Теория пар сил
- Силы, направленные в одну сторону
- Силы направлены в противоположные стороны и различные по модулю
- Пара сил и ее момент
- Эквивалентность пары сил
- Добавление пар сил
- Условия равновесия пар сил
- Момент силы относительно точки на оси. Момент пары сил
- Момент силы относительно точки
- Теорема о моменте равнодействующей системы сходящихся сил
- Момент сил относительно оси
- Момент пары сил и его свойства
Парой сил называется система двух равных по модулю, противоположных по направлению параллельных сил.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Теория пар сил
Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы.
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны. Пара сил не составляет системы сил, эквивалентной нулю. Пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.
Пара сил, действующая на твердое тело, характеризуется, прежде всего, плоскостью действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.
Силы, направленные в одну сторону
Пусть в абсолютно твердого тела в точках А и В приложены две параллельные силы




Поскольку 








Итак,
Силы 

действия имеют точку пересечения А. Перенесем силы 

Сила — скользящий вектор, поэтому 




Получим:
Поскольку силы 








Найдем точку приложения равнодействующей 



Поскольку

Итак, равнодействующая двух параллельных сил, направленных в одну сторону, параллельна этих сил, направленная в ту же сторону, что и составляющие силы; модуль
равнодействующей равна сумме модулей составляющих сил, а линия ее действия разделяет расстояние между точками приложения этих сил внутри на части, обратно
пропорциональны величинам этих сил.
Из изложенного следует, что произвольную силу можно разложить на две параллельные силы. Если 
Силы направлены в противоположные стороны и различные по модулю
Пусть параллельные силы 



Найдем равнодействующую сил 








Согласно (4.3), 
Поскольку 




Равнодействующая двух параллельных, разных по модулю, противоположно направленных сил параллельная им и направлена в сторону большей силы; модуль равнодействующей равна разности модулей составляющих сил. Линия действия равнодействующей 
Пара сил и ее момент
Система двух равных по модулю, параллельных, противоположно направленных сил, линии действия которых не совпадают, называется парой сил.
Пусть к некоторому абсолютно твердого тела приложена пара сил 
Согласно определению пары сил:
Элементами пары есть силы, составляющие пару, плечо пары, плоскость действия пары.
Плечо пары — это кратчайшее расстояние между линиями действия сил пары, то есть длина перпендикуляра h, опущенного из любой точки линии действия одной из сил пары на линию действия второй силы (рис. 4.3, а). Поскольку сила -скользящий вектор, то силы в паре всегда можно разместить так, чтобы расстояние АВ между точками их приложения было плечом пары (Рис. 4.3, б).
Плоскость действия пары — это плоскость, в которой размещены силы пара. Она единственная, поскольку через две параллельные линии можно провести только одну
плоскость.
Как будет показано в § 5.3, пара сил не имеет равнодействующей.
Пара сил не является системой уравновешенных сил, ибо в первой аксиомой статики две равные по модулю и противоположны по направлению силы будут уравновешенной системой сил только тогда, когда имеют общую линию действия. Силы, составляющих пару, не имеют общей линии действия.
Пара сил, действующая на тело, пытается вращать его. По мере вращательного действия силы в статике, как известно, является момент. Следовательно, и действие пары сил на тело должна характеризоваться моментом. Докажем это с помощью следующей теоремы.
Теорема 4.1. Векторная сумма моментов сил пары относительно произвольного центра
(Точки) в пространстве является величиной постоянной для данной пары.
Доказательство. Пусть задано пару сил
действие пары на тело характеризуется вращательным эффектом, найдем сумму моментов сил пары относительно центра О, произвольно расположенного в пространстве.
Получим:
где 


Здесь 


Известно, что вектор 


Аналогично, учитывая, что 
где вектор 


Следовательно, сумма моментов сил пары относительно произвольного центра в пространстве не зависит от выбора этого центра и равен моменту одной из сил пары относительно точки приложения другой силы. Теорема доказана.
Эта сумма моментов характеризует вращательное действие пары сил на тело. Назовем ее вектор-моментом пары сил. Обозначим вектор-момент пары сил 


С доказательства теоремы следует, что момент пары сил является вектором. Определим его величину и направление.
Величина момента пары по формулам (4.10) — (4.14) равна произведения величины одной из сил пары на плечо пары:
Вектор-момент пары сил направляется перпендикулярно к плоскости действия пары так, чтобы с его конца было видно попытки пары сил вращать тело против часовой стрелки (рис. 4.4).
Если на тело действует система пары сил, расположенных в одной плоскости, то вектор-моменты всех пар сил системы перпендикулярны этой плоскости. Итак, вектор-моменты такой системы пар является системой параллельных векторов, для составления которых достаточно знать их величины и знаки. Поэтому целесообразно ввести понятие алгебраического момента пары сил.
Алгебраическим моментом пары сил называется взятый со знаком «+» или «-» произведение одной из сил пары на плечо пары:
Алгебраический момент пары сил считаем положительным, если пара сил пытается вращать тело против часовой стрелки (рис. 4.5, а) и отрицательным, если пара сил пытается вращать тело по часовой стрелке (рис. 4.5, б). Алгебраические моменты пар сил на рисунках показывают дуговыми стрелками.
Эквивалентность пары сил
Рассмотрим теоремы, из которых вытекают основные свойства пары сил, которые предоставят нам возможность выполнять определенные действия над ними.
Теорема 4.2. Действие пары сил на тело не изменится при произвольном переносе этой пары в плоскости ее действия.
Доказательство. Пусть к некоторому телу приложена пара сил 


Силы выбираем так, чтобы
Согласно второй аксиомой статики
Перенесем силы 





Учитывая формулы (4.7) и (4.17), получим
Поскольку фигура 

и 











Это означает согласно формуле (4.18), заданной паре сил 

Покажем, что величина и направление векторов-моментов пар сил 


Из рис. 4.8 видно, что знак момента 



Теорема 4.3. Действие пары сил на твердое тело не изменится, если перенести эту пару в плоскость, параллельную плоскости ее действия.
Доказательство. Пусть на некоторое твердое тело действует пара сил 

Выберем в теле плоскость 



Приложим к телу в точках С и D две системы уравновешенных сил 

Проведем отрезки АС и ВD, точкой пересечения которых есть точка А.
Поскольку 

Добавим попарно силы 





Равнодействующая силы 

стороны. Итак, система сил 
и можно записать
Сравнивая соотношения (4.21) и (4.22), получим 


Вектор-моменты





Теорема доказана.
Теорема 4.4. Действие пары на тело не изменится, если изменить силы и плечо пары, оставляя неизменным ее вектор-момент.
Доказательство. Пусть к телу приложена пара сил 
Приложим к телу в точках А и В две силы 

За аксиомой параллелограмма сил найдем равнодействующие систем сил 

Учитывая, что 

Итак, 


силы

Плечо новой пары 


видно, что поскольку 







Из доказанных теорем следует:
1) пары эквивалентны, если равны их векторы-моменты;
2) вектор-момент пары сил является вектором свободным. Это означает, что его можно приложить в произвольной точке твердого тела.
Сформулированы три теоремы можно объединить в одну теорему: пары сил являются эквивалентными, если равны их векторы-моменты.
Из всего сказанного можно сделать вывод, что вектор-момент пары сил является полной характеристикой статическому воздействию пары на твердое тело. Поэтому действия над парами сил можно заменить эквивалентными операциями над их векторами-моментами.
Добавление пар сил
1. Геометрическое определение момента результирующей пары сил
Установим правило сложения пар сил, лежащих в плоскостях, которые пересекаются. Это правило вытекает из следующей теоремы.
Теорема 4.5. Две пары сил, которые лежат в плоскостях, пересекающихся эквивалентны одной паре, вектор-момент которой равен геометрической сумме векторов-моментов данных пар.
Доказательство. Пусть пары сил

Пользуясь теоремой 4.4, приведем обе пары к плечу АВ, размещенного на линии пересечения плоскостей П1 и П2 , то есть
При этом должны выполняться равенства

Добавим согласно аксиоме параллелограмма силы, приложенные в точках А и В. Получим 







Теорема доказана.
Аналогично можно добавить n пар сил в пространстве. В результате получим одну пару сил, вектор-момент которой равен векторной сумме векторивмоментив составляющих пар сил, а именно:
2. Аналитическое определение момента результирующей пары сил
Спроектируем равенство (4.25) на оси прямоугольной декартовой системы координат и используем теорему о проекции суммарного вектора на ось. Получим проекции момента результирующей пары сил на оси координат:
где 


и-й пары на оси выбранной системы координат.
Тогда величина вектора момента пары
а направление его найдем по формулам:
Известно (§ 4.2), что вектор-моменты пар, размещенных в одной плоскости, есть коллинеарными и поэтому добавляются алгебраически. Итак, момент результирующей
пары плоской системы пар равна сумме алгебраических моментов составляющих пар
Условия равновесия пар сил
1. Геометрическое условие равновесия пространственной системы пар сил
Пусть на тело действует n пар сил, произвольно расположенных в пространстве, вектори-моменты которых равны
В § 4.4 было доказано, что такая система пар сил эквивалентна одной паре сил, вектор-момент которой определяется формулой (4.25). очевидно, что тело под действием системы пар сил остается в равновесии, если вектор-момент результирующей пары будет равняться нулю
Это условие равновесия, учитывая формулу (4.25), запишем в виде
Формула (4.29) является геометрической условием равновесия пространственной системы пар, которую можно сформулировать так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда вектор-момент результирующей пары или геометрическая сумма векторов-моментов составляющих пар будет равняться нулю.
2. Аналитические условия равновесия пространственной системы пар сил
Из условия (4.29), учитывая формулу (4.26), получаем, что в случае равновесия пространственной системы пар сил то есть
Формулы (4.30) являются аналитическими условиями равновесия пространственной системы пар сил, которые формулируются так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда алгебраические суммы проекций
векторов-моментов составляющих пар на три взаимно перпендикулярные оси координат будут равны нулю.
3. Условие равновесия плоской системы пар сил
Условие равновесия плоской системы пар сил получаем из равенства (4.28).
Плоская система пар сил будет находиться в равновесии тогда и только тогда, когда сумма алгебраических моментов составляющих пар сил будет равняться нулю:
Условие равновесия плоской системы пар можно получить также из условий равновесия (4.30).
Действительно, пусть система пар сил размещена в координатной плоскости 



Поскольку 

Момент силы относительно точки на оси. Момент пары сил
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны, приложенных к телу в двух разных точках.
Момент силы относительно точки
Моментом силы 





Модуль этого векторного произведения:

Опустим перпендикуляр из точки 





Итак, момент силы относительно центра 
плечо, и направленный перпендикулярно к плоскости, проходящей через точку 


Очевидно, момент силы относительно точки имеет все свойства векторного произведения. Из формулы (2.1) можно найти проекции вектора 

Раскрывая этот определитель по элементам первой строки и раскладывая вектор 



Сравнивая левую и правую части равенства (2.5), имеем

Модуль, и направление момента силы относительно точки можно определить еще и так:
Заметим, что формулы (2.6) легко получить, пользуясь правилом циклической
перестановки индексов.
По определению момента силы относительно точки имеем:
1) если переместить силу вдоль линии ее действия, то момент силы относительно точки не изменится;
2) момент силы относительно точки всегда равен нулю, когда линия действия силы проходит через эту точку (в этом случае плече 
3) момент силы относительно точки численно равен удвоенной площади треугольника 

Теорема о моменте равнодействующей системы сходящихся сил
Теорема Вариньона. Момент равнодействующей сходящейся системы сил относительно произвольного центра равен векторной (геометрической) сумме моментов составляющих сил относительно того самого центра:

Доказательство. Пусть в точке А пересекаются линии действия системы сходящихся сил




получим:

что и требовалось доказать.
Если силы и точка О размещены в одной плоскости, то их моменты перпендикулярны этой плоскости и лежат на одной прямой. Поэтому момент равнодействующей такой системы сил равен алгебраической сумме моментов составляющих сил относительно этой
точки.
Момент сил относительно оси
Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси (рис. 2.5).
Из этого определения следует, что моменты сил относительно координатных осей вычисляются по формулам (2.6). Эти формулы, в частности, показывают, что момент силы
относительно оси не зависит от выбора точки на оси.
При решении конкретных задач моменты сил относительно осей удобно вычислять более наглядным способом (рис. 2.6) по следующему правилу.
1. Проводим произвольную плоскость 

пересечения этой плоскости с осью.
2. Проектируем силу 
3. Вычисляем момент проекции 

При этом момент силы относительно оси считается положительным, если наблюдатель видит со стороны положительного направления оси 


Как видно из рис. 2.6, численное значение момента силы относительно оси 

Из определения момента силы относительно оси следует, что он равен нулю, если линия действия силы и ось лежат в одной плоскости.
Пример 1. Сила 
с осью 





Вычислить момент этой силы относительно оси
Решение.
По формулам (2.6), есть


Известно, что 
или
Если 

Если 

Момент пары сил и его свойства
Парой сил называется система двух равных по величине сил 


Определим, чему равна сумма моментов сил, составляющих пар относительно произвольной точки.
Пусть О — произвольная точка пространства (Рис. 2.7, б), a 


Полученная векторная сумма не зависит от положение точки 
Векторное произведение


плечо пары.
Как видим, момент пары направленный перпендикулярно к плоскости действия пары в ту
сторону, откуда «вращение» пары происходит против часовой стрелки.
Итак, момент пары сил — вектор свободный и математически определен в виде

Ниже показано, что момент пары полностью определяет статическое действие пары сил на твердое тело, то есть полной характеристикой механического воздействия пары сил на это тело. Из определения момента пары сил и аксиомы I о двух силах следует, что пара сил является уравновешенной системой (система сил, эквивалентная нулю) тогда и только тогда, когда момент пары равна нулю. Другие свойства пары сил определяются следующими теоремами.
Теорема 1. Не меняя действия пары сил на твердое тело, его можно переносить и произвольно вращать в плоскости действия, изменяя величину силы, входящей в нее, и длину плеча так, чтобы момент пары оставался неизменным.
Доказательство. Пусть задано пару сил



на линиях, перпендикулярные к нему, приложим соответственно две системы сил







Перенесем теперь силы 



















Покажем, что при указанном перемещении пары сил можно изменять величину
силы, входящей в нее, и длину плеча, о чем говорится в теореме. Для этого рассмотрим исходную пару сил 
Приложим к точкам а и b систему сил 

равнодействующие сходящихся систему сил










Теорема 2. Две пары сил, которые лежат в одной или параллельных плоскостях и имеют одинаковые по величине, но противоположные по направлению моменты, составляют систему пар сил, эквивалентную нулю.
Доказательство. Пусть в плоскости заданы две пары сил 







С другой стороны, сумма моментов всех сил, которые составляют эти пары, определяется выражением:

которое является суммой моментов составляющих пар, равных нулю. Следовательно, эта система двух пар сил эквивалентна нулю.
Поскольку момент пары сил — вектор свободный, то доказанные теоремы справедливы также для случая пар сил, лежащих в параллельных плоскостях.
Из доказанных теорем следует вывод об эквивалентности двух пар сил, имеющих геометрически одинаковые моменты.
Кроме того, эти теоремы позволяют установить правило составления пар сил, которые лежат не только в параллельных плоскостях, но и в тех, которые пересекаются.
Так, если задан систему n пар 



Отметим, что пару сил нельзя заменить одной силой, которая была бы эквивалентна по действию на твердое тело двум равным по величиной, параллельным и противоположно направленным силам. Действительно, если предположить, что пара сил эквивалентна некоторой силе 



Итак, пара сил, действующих на твердое тело, образует новый самостоятельный элемент статики, который вместе с силой составляет важное понятия механики. Основные свойства этого элемента и основные преобразования, которым он подлежит, вполне устанавливаются доказанными теоремами о парах.
Эти свойства и превращения будут выглядеть так:
1) пару сил можно переносить в плоскости ее действия, в том числе и вращать на любой угол;
2) пару сил можно переносить в любую плоскость, параллельную плоскости действия этой пары;
3) можно изменять силы, образующие пару и плечо, не меняя момента пары;
4) несколько пар сил, произвольно расположенных в пространстве, можно заменить одной парой, момент которой равен геометрической сумме моментов составляющих пар.
Из изложенного в главах 1 и 2 приходим к такому важному выводу: механическое влияние в статике характеризуется тремя типами векторов: силой — скользящим вектором, моментом силы относительно точки — приложенным вектором и парой сил — свободным вектором.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки

Момент силы относительно оси равен проекции вектора момента на эту ось. Примеры вычисления момента силы относительно центра и относительно оси приведены на рис.2.16
M z (F )= M z (F )k = rxy ×Fxy , M z (F ) = Fxy d , M z (F )= MO (F ) cos(α).
Момент силы относительно оси равен нулю если:
•Вектор силы параллелен оси,
•Вектор силы пересекает ось (плечо силы равно нулю).
Пара сил. Момент пары
Две равные по величине и противоположно направленные силы образуют пару сил, если линии их действия не совпадают (рис.2.17).
Пара сил характеризуется плоскостью действия, направлением вращательного действия, величиной момента пары.
M (F ; F ′)
F
d
F′
Рис.2.17 Пара сил, момент пары
Силы пары не образуют уравновешенную систему сил, хотя геометрическая сумма сил пары равна нулю.
Сумма моментов сил, составляющих пару, не зависит от выбора центра и равна произведению силы пары на плечо пары.
Докажем эту теорему: пусть в плоскости «П» действует пара сил ( F; F′).
Определим вектор-момент пары, как сумму моментов каждой из сил, относительно одного и того же центра О, выбранного произвольно. Учтем, что силы пары противоположны по направлению(F = −F′). Радиусывекторы
50
Пара сил:
Парой сил называют систему двух численно равных параллельных сил, направленных в противоположные стороны
Пара сил и ее момент. Равнодействующая двух не равных по модулю параллельных сил, направленных в противоположные стороны, равна их разности. Если же такие силы по модулю равны, то они не имеют равнодействующей. Они и не уравновешивают друг друга, за исключением того частного случая, когда они имеют одну общую линию действия. Систему двух численно равных параллельных сил, приложенных к одному телу и направленных в противоположные стороны, называют парой сил.
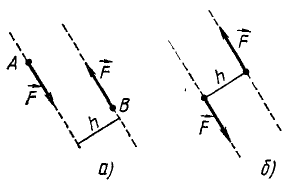
Пусть на тело (рис. 39, а) действует пара сил, причем одна из сил пары приложена в точке А, а другая в точке В. (Тело на рисунке не показано.) Назовем плечом пары кратчайшее расстояние (длину перпендикуляра) между линиями действия сил пары. Сила является скользящим вектором, поэтому силы пары (или одну из них) можно перенести в такое положение (рис. 39, б), чтобы на чертеже отрезок, соединяющий точки их приложения, был перпендикулярен линиям действия сил, т. е. изображал бы плечо.
Плоскость, в которой лежат линии действия сил пары, называют плоскостью пары.
Механическое воздействие пары сил на твердое тело зависит не только от величины сил, но в равной степени также и от плеча. Поэтому за меру механического воздействия пары сил на твердое тело принимают момент пары—величину, численно равную произведению модуля силы на плечо пары:
M=hF. (24)
Момент пары, подобно моменту силы относительно точки,— векторная величина. Вектор момента пары перпендикулярен плоскости пары. Но у всякой плоскости имеется две стороны. Условились вектор момента восставлять с той стороны, с которой пара представляется поворачивающей свое плечо против хода часов (рис. 40). Таким образом, вектор момента пары сил характеризует не только величину воздействия пары на тело, но также и плоскость пары и направление, в котором силы пары стремятся повернуть тело.
В частном случае плоской системы сил момент пары рассматривают как алгебраическую величину и считают положительным, если силы пары стремятся повернуть плечо против вращения стрелок часов, если же силы пары стремятся повернуть плечо по ходу часов, то момент считают отрицательным (рис. 41).
Сумма моментов двух сил пары относительно любой точки пространства равна моменту пары
Свойства пары
Чтобы лучше пояснить понятие пары сил—одно из важнейших понятий механики, покажем, что момент пары сил равен сумме моментов двух сил пары относительно произвольно взятой точки. Для упрощения доказательства мы предположим сначала, что эта точка находится в плоскости пары, а затем распространим теорему на любую точку.
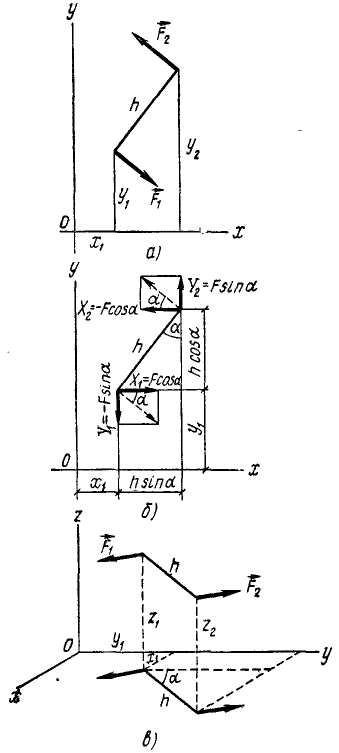
В плоскости пары возьмем совершенно произвольно какую-либо точку О, примем ее за начало плоской системы координат (рис. 42, а), проведем через нее в произвольном направлении ось Ox и перпендикулярно к ней ось Оу. По формуле (16) определим моменты сил пары относительно этой точки О, выбранной нами произвольно и принятой за начало координат:
Но, как видно из чертежа (рис. 42, б),
Подставляя эти величины и складывая, определим сумму моментов двух сил лары относительно точки О:
Таким образом, сумма моментов двух сил пары относительно любой точки О, взятой на ее плоскости, не зависит от их относительного положения (расстояния и ориентации) и равна моменту пары. Отсюда мы можем сделать вывод, что момент пары сил не изменится, если эту точку заменить какой-либо другой или если пару перенести в любое другое место ее плоскости, или повернуть на любой угол в ее плоскости.
Рассмотрим теперь самый общий случай, т. е. не будем накладывать никаких ограничений на положение пары сил и центра моментов. Примем произвольно взятую точку О (рис. 42, в) за начало прямоугольной системы координат, проведем плоскость хОу параллельно плоскости пары, направим оси Ox и Oy произвольно в этой плоскости, а ось Oz-перпендикулярно к ней. Тогда координаты точек приложения сил пары и проекции сил на оси выразятся равенствами, подобными только что написанным, лишь с добавлением третьей координаты, и мы будем иметь:
Учитывая написанные значения координат и проекций сил, определим по (23) суммы моментов двух сил пары относительно координатных осей. Относительно оси Ox получим
Рис. 42
Аналогично относительно оси Oy
и относительно оси Oz
Теперь по формуле (22) находим, что модуль вектора суммы моментов двух сил пары относительно произвольно взятого центра О равен произведению модуля силы пары на плечо пары. Направлен этот вектор по оси Oz, т. е. перпендикулярно к плоскости пары сил.
Мы убедились, что сумма моментов двух сил пары относительно точки О равна моменту пары вне зависимости не только от положения пары в ее плоскости, но также и от расстояние плоскости пары от центра моментов. Иными словами, момент пары не изменится, если пару перенести в параллельную плоскость.
Момент пары выражается свободным вектором, перпендикулярным к плоскости пары, численно равным произведению силы на плечо
Как уже было сказано, момент пары является мерой механического воздействия пары сил на тело, а потому механическое воздействие пары сил на твердое тело не изменяется, если эту пару поворачивают в ее плоскости, переносят в другое место плоскости или в параллельную плоскость.
Эти на первый взгляд парадоксальные свойства пары поясним примерами. Гаечный ключ (рис. 43) одинаково действует на гайку, к каким бы граням этой гайки его ни приложить — момент пары не изменится от поворота пары сил в ее плоскости. Трансмиссионный вал (рис. 44) сообщает шкиву вращающий момент независимо от места закрепления шкива на валу — момент пары не изменится от переноса пары в параллельную плоскость.
Но только при изучении динамики, после знакомства с инерцией вращающегося тела и с понятием главных центральных осей, когда читатель узнает, что вращение тела зависит от массы каждой частицы тела и от их распределения, ему станет совершенно ясно, почему Действие пары сил на тело не зависит от положения пары сил в ее плоскости.
Момент пары сил не имеет фиксированной, определенной точки приложения. Он является свободным вектором, т. е. он имеет свою величину и свое направление, но приложить его можно в любой точке твердого тела, на которое действует пара сил. В этом заключается принципиальное отличие момента пары от момента силы относительно точки, являющегося прикрепленным вектором, приложенным в центре момента, или от скользящего вектора, примером которого является сила.
Две пары сил с равными моментами эквивалентны
Эквивалентность пар
Обратим особое внимание на то, что момент пары не является только произведением, а есть мера, полностью характеризующая воздействие пары сил на твердое тело. Две пары с одинаковыми моментами оказывают на тело одинаковое действие, если даже силы одной пары (а также и плечо) не равны силам (и плечу) другой пары.
Докажем сначала, что данную пару (F1F2), модули сил которой F, а плечо AB (рис. 45, а), можно, не изменяя ее механического воздействия на твердое тело (тело на рис. 45 не показано), заменить другой парой с таким же моментом, но с большими силами и соответственно меньшим плечом.
Приложим к телу в точке В, как показано на рис. 45, б, две взаимно уравновешенные силы 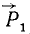
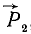
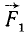
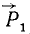
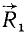
Складывая силы 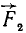
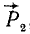
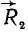
Новую пару сил (R1R2) мы получили из данной пары (F1F2), присоединив к ней взаимно уравновешенные силы P1 и P2. Следовательно, обе пары эквивалентны. Момент новой пары равен
или, принимая во внимание написанную выше пропорцию, из которой следует, что P . BC = F . AC, получим
т. е. моменты эквивалентных пар равны между собой и данную пару мы заменили другой парой с тем же моментом, но с меньшим плечом.
Чтобы убедиться, что всякую пару сил (F1F2) можно заменить другой парой сил с тем же моментом, но с большим плечом и соответственно с меньшими силами, сложим (см. рис. 45, б) силы F1 с P2, F2 с P1. Мы получим новую пару (Q1Q2) (рис. 45, г) с моментом
что и требовалось доказать.
Следовательно, механическое воздействие пары на твердое тело не изменится, если эту пару заменить любой другой парой с таким же моментом. ,Момент пары является свободным вектором, поэтому
эквивалентные пары находятся в одной или в параллельных плоскостях.
Момент пары сил, полученной от сложения нескольких пар, равен сумме моментов слагаемых пар.
- Заказать решение задач по теоретической механике
Сложение пар
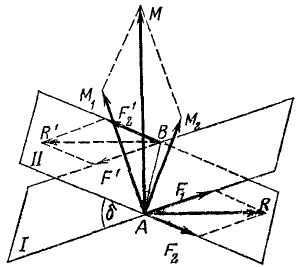
Покажем, что несколько пар, приложенных к твердому телу, эквивалентны одной паре, момент которой равен сумме их моментов. Пусть к некоторому телу приложены две пары сил, одна из которых лежит в плоскости l и имеет момент M1, а другая — в плоскости ll и имеет момент M2. Для общности доказательства предположим, что эти плоскости не пересекаются под углом δ. Воспользовавшись только что доказанными свойствами пар, представим каждую данную пару парой, ей эквивалентной, лежащей в той же плоскости и имеющей плечо AB (рис. 46), расположенное по линии пересечения обеих плоскостей. Модули сил F1 первой пары и F2—второй определим из условия эквивалентности
Рис. 46
Сложим силы обеих пар, приложенные к телу в точке А, а затем сложим силы, приложенные в точке В. Получим два параллелограмма сил с вершинами в точках А и В. Эти параллелограммы равны между собой, так как попарно равны и параллельны их стороны. Следовательно, равны и параллельны диагонали параллелограммов.
В результате сложения двух пар мы получили одну пару сил c тем же плечом и с силами, равными геометрической сумме соответствующих сил слагаемых пар. Найдем момент M этой пары.
На векторах моментов M1 и M2 построим как на сторонах параллелограмм, называемый параллелограммом моментов. Диагональ этого параллелограмма по величине и по направлению изображает момент пары (RR’), полученной в результате сложения пар (F1, F1/) и (F2, F2/). В самом деле, стороны параллелограмма моментов перпендикулярны и пропорциональны сторонам параллелограмма сил, а потому и диагональ параллелограмма моментов перпендикулярна плоскости пары и равна R.АВ.
Мы пришли к заключению, что для сложения двух пар, лежащих в пересекающихся плоскостях, достаточно сложить их моменты. Но методом доказательства от n к n+1 нетрудно показать, что теорема остается справедливой для любого количества пар сил, т. е.
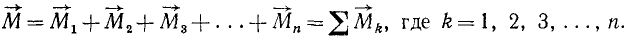
Если сумма моментов всех пар равна нулю, то система пар находится в равновесии, так как наличие такой системы эквивалентно ее отсутствию. Справедливо и обратное заключение: если система пар находится в равновесии, то сумма моментов всех пар системы равна нулю. Таким образом, необходимым и достаточным условием равновесия системы пар, не лежащих в одной плоскости, является равенство нулю геометрической суммы моментов всех пар системы:
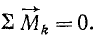
Момент пары является векторной величиной, а потому суммирование надо производить, разумеется, геометрически, т. е. по правилу параллелограмма. В частном, но очень важном случае (имеющем большое применение в технике), когда пары расположены в одной плоскости, сложение моментов производят алгебраически. В самом деле. Будем поворачивать плоскости l и ll на рис. 46 до их совпадения. Тогда угол δ станет равным нулю, параллелограммы выродятся в отрезки прямой и геометрические суммы сил и сумма моментов превратятся в сложение векторов, направленных по прямой, т. е. в алгебраическое сложение.
Поэтому, чтобы сложить пары сил, расположенные в одной плоскости, достаточно алгебраически сложить их моменты:
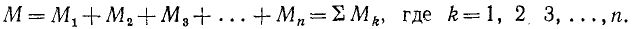
Необходимым и достаточным условием равновесия системы пар, лежащих в одной плоскости, является равенство нулю алгебраической суммы моментов всех пар системы:
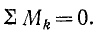
Задача №1
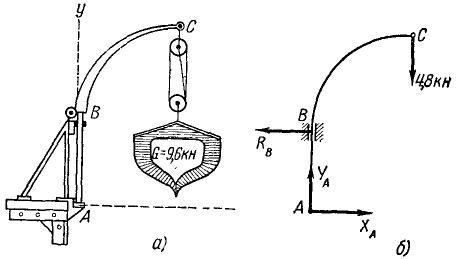
Шлюпка (рис. 47, а) висит на двух шлюпбалках, причем вес ее, равный 960 кГ, распределяется между ними поровну. Шлюпбалка ABC нижним полушаровым концом опирается на подпятник Л и на высоте 1,8 .и над ним свободно проходит через подшипник B-, вылет шлюпбалки равен 2,4 м. Пренебрегая весом шлюпбалки, определить давление ее на опоры А и В.
Решение. Требуется определить давление на опоры, но мы будем определять реакции в опорах и рассмотрим для этого равновесие шлюпбалки. Какие же силы действуют на шлюпбалку? На одну шлюпбалку приходится половина веса шлюпки (480 кГ). Эта сила приложена в точке C (рис. 47, б) и направлена вертикально вниз.
В точках А и В на шлюпбалку наложены связи, и в этих точках приложены реакции связей, равные и противоположные давлениям на опоры.
Подшипник В допускает перемещение по вертикали, следовательно, реакция связи, направленная, как известно, перпендикулярно виртуальным перемещениям, горизонтальна. Очевидно, она направлена влево, так как шлюпбалка давит на подшипник вправо.
Рис. 47
Направление реакции в шарнире обычно бывает неизвестным, поэтому реакцию в подшипнике разложим на две составляющие Xa и Ya, направленные, как показано на чертеже.
Мы видим, что система сил, приложенных к шлюпбалке, представляет собой две пары сил. Для равновесия такой системы необходимо и достаточно выполнение условия (26)
Заметим, что момент пары (RB, XA) положителен, так как эта пара стремится повернуть шлюпбалку против часовой стрелки, а момент (0,5G, YA) отрицателен, потому что под действием этой пары шлюпбалка стремится повернуться по ходу часовой стрелки. Из написанного уравнения находим RB = 640 кГ. Векторы сил пары равны и противоположны, следовательно, реакция XA = 640 кГ и направлена вправо, реакция YA = 480 кГ и направлена вверх, а давления направлены в обратные стороны.
Ответ. XA =— 6,4 кн, YA=— 4,8 кн, XB =— 6,4 кн.
Задача №2
К окружности трех дисков: А — радиуса 15 см (рис. 48, а), В —радиуса 10 см и С—радиуса 5 см приложены пары сил; величины сил, составляющих пары, соответственно равны 10 кГ, 20 кГ и P. Оси OA, OB и ОС лежат водной плоскости. Угол AOB — прямой. Определить величину силы P и угол BOC = а так, чтобы система трех дисков, будучи совершенно свободной, оставалась в равновесии.
Решение. Рассмотрим равновесие твердого тела, представляющего собой три пересекающиеся оси OA, OB и ОС, на которые жестко насажены диски. К окружностям дисков приложены три пары, две из которых известны, у третьей известно только плечо. Представим моменты этих пар в виде векторов (рис. 48, б), направленных перпендикулярно плоскостям дисков и численно равных: М1= 150 н . см, М2 = 200 н . см и М3 = 5P. По условию равновесия (26) геометрическая сумма моментов пар должна равняться нулю, следовательно, треугольник моментов должен быть замкнут. Отсюда следует, что оси OA, OB и ОС лежат в одной плоскости. Решая треугольник, легко получаем ответ.
Ответ. P = 50 н, α = arctg (—0,75) = 143°10′.
- Приведение системы сил к данной точке
- Система сил на плоскости
- Естественный и векторный способы определения движения точки
- Координатный способ определения движения точки
- Теорема кинетической энергии
- Условие равновесия системы сходящихся сил в геометрической форме
- Условия равновесия системы сходящихся сил в аналитической форме
- Приведение двух параллельных сил к равнодействующей
Определить момент результирующей пары, эквивалентной системе трех пар, лежащих в одной плоскости. Первая пара образована силами P1 = P’1 = 2 кн, имеет плечо h1= 1,25 м и вращает по часовой стрелке; вторая пара образована силами P2 = P’2 = 3 кн, имеет плечо h2 = 2 м и вращает против часовой стрелки; третья пара образована силами P3 = P’3 = 4,5 кн, имеет плечо h3 = 1,2 м и вращает по часовой стрелке (см.рис.).
Решение. Вычисляем моменты составляющих пар:
М1 = P1·h1 = 2 ·1,25 = 2,5 кн·м;
М2 = —P2·h2 = —3 ·2 = —6 кн·м;
М3 = P3·h3 = 4,5 ·1,2 = 5,4кн·м.
Для определения момента результирующей пары складываем алгебраически моменты заданных пар
М = М1 + М2+ М3 = 2,5 — 6 + 5,4 = 1,9 кн·м.