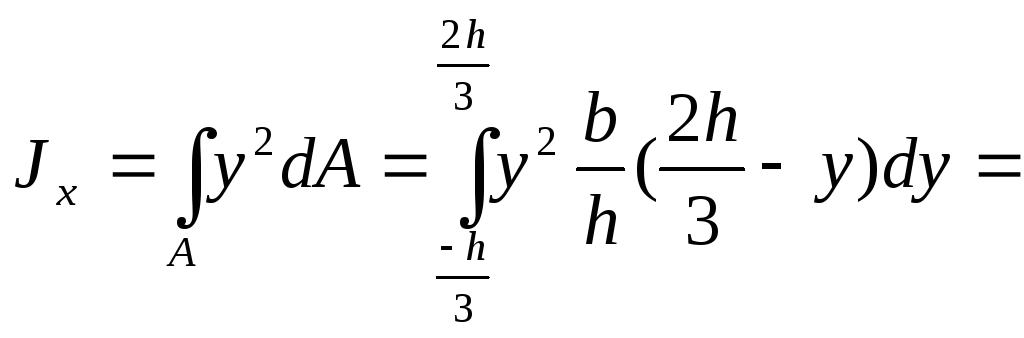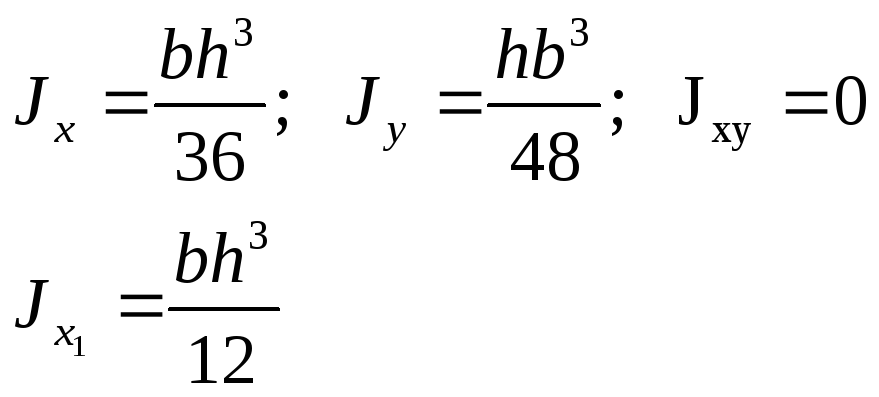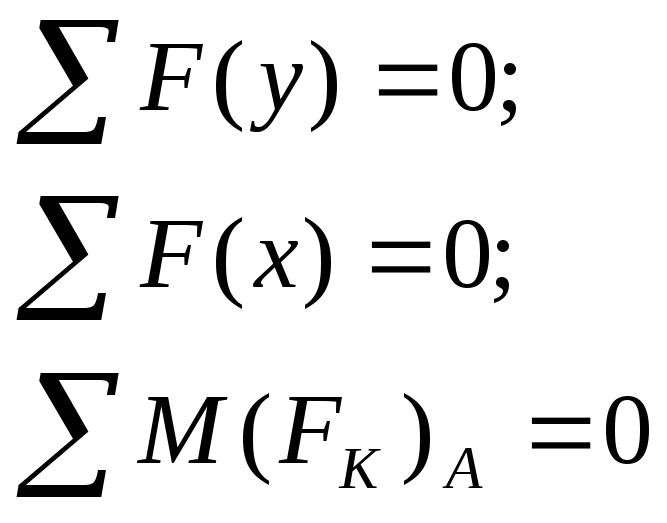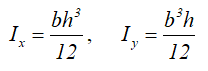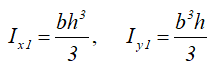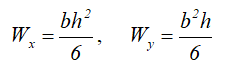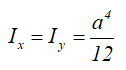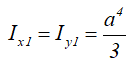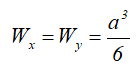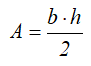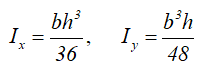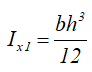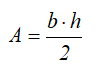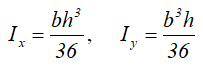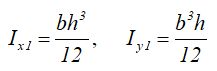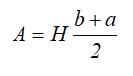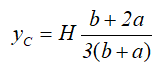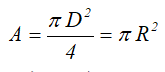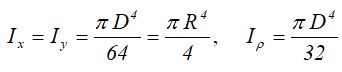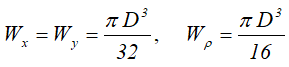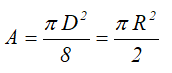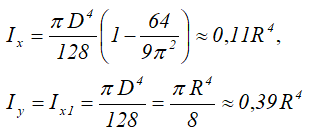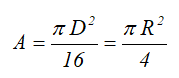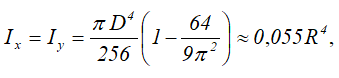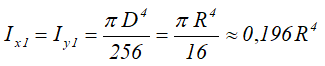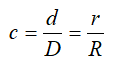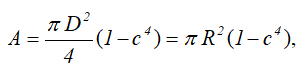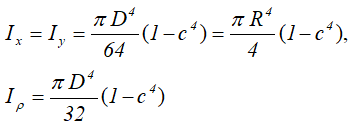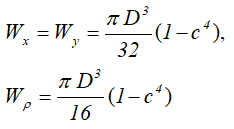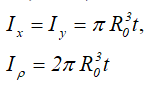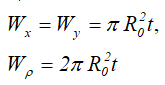Осевые моменты инерции простых сечений (фигур)
На этой странице указаны формулы для расчёта моментов инерции простых сечений (фигур). Данные формулы используются при проведении прочностных расчётов при изгибе и расчётов на жёсткость. А также для расчёта геометрических характеристик более сложных сечений.
Формулы для расчёта осевых моментов инерции
Традиционно, моменты инерции обозначаются буквой – I. Также в литературе, часто используют букву – J.
На сайте – ssopromat.ru, ты также можешь найти другую справочную информацию.
Прямоугольное
сечение.
Прямоугольное
сечение имеет две оси симметрии, а
главные центральные оси Сx
и Cy
проходят через середины параллельных
сторон.
Главный
центральный момент инерции относительно
оси x
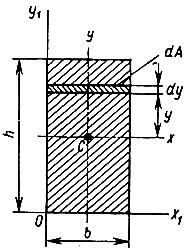
Элементарную
площадку dA
в этом случае можно представить в виде
полоски во всю ширину сечения и толщиной
dy,
значит dA=b*dy.
Подставим под знак интеграла значение
dA
и проинтегрировав по всей площади, т.е.
в пределах изменения ординаты y
от –h/2
до +h/2,
получим
Окончательно
Аналогично
получим формулу главного центрального
момента инерции прямоугольника
относительно оси y:
Круглое
сечение
Для
круга главные центральные моменты
инерции относительно осей x
и y
равны между собой.
Поэтому
из равенства
Треугольник
2.Изменение моментов инерции при переходе от центральных осей к параллельным:
Jx1=Jx
+ a2А;
Jy1=Jy
+ b2А;
момент
инерции относительно любой оси равен
моменту инерции относительно центральной
оси, параллельной данной, плюс произведение
площади фигуры на квадрат расстояния
между осями. Jy1x1=Jyx
+ abF;
(«a»
и «b»
подставляют в формулу с учетом их знака).
3.Изменение моментов инерции при повороте осей
Jx1=Jxcos2
+ Jysin2
— Jxysin2;
Jy1=Jycos2
+ Jxsin2
+ Jxysin2;
Jx1y1=(Jx
— Jy)sin2
+ Jxycos2
;
Угол
>0,
если переход от старой системы координат
к новой происходит против час.стр. Jy1
+ Jx1=
Jy
+ Jx
Экстремальные
(максимальное и минимальное) значения
моментов инерции называются главными
моментами инерции.
Оси, относительно которых осевые моменты
инерции имеют экстремальные значения,
называются главными
осями инерции.
Главные оси инерции взаимно перпендикулярны.
Центробежные моменты инерции относительно
главных осей = 0, т.е. главные оси инерции
— оси, относительно которых центробежный
момент инерции = 0. Если одна из осей
совпадает или обе совпадают с осью
симметрии, то они главные. Угол,
определяющий положение главных осей:
,
если
0>0
оси поворачиваются против час.стр. Ось
максимума всегда составляет меньший
угол с той из осей, относительно которой
момент инерции имеет большее значение.
Главные оси, проходящие через центр
тяжести, называются главными
центральными осями инерции.
Моменты инерции относительно этих осей:
Jmax
+ Jmin=
Jx
+ Jy.
Центробежный момент инерции относительно
главных центральных осей инерции равен
0. Если известны главные моменты инерции,
то формулы перехода к повернутым осям:
Jx1=Jmaxcos2
+ Jminsin2;
Jy1=Jmaxcos2
+ Jminsin2;
Jx1y1=(Jmax
— Jmin)sin2;
4.Классификация элементов конструкций
Стержнем
наз. Геом тела у которых один из размеров
много больше других.
Пластины
или оболочки
– это геом тела у которых один из размеров
<< других
Массивные
тела—
все размеры одного порядка
5.Основные
допущения о свойствах материала
Однородные
– в люб. точке материалы имеют одинак.
физико-химич. св-ва;
Сплошная
среда – кристаллич. строение и микроскопич.
дефекты не учитываются;
Изотропны
– механич. св-ва не зависят от направления
нагружения;
Идеальная
упругость – полностью восстанавливают
форму и размеры после снятия нагрузки.
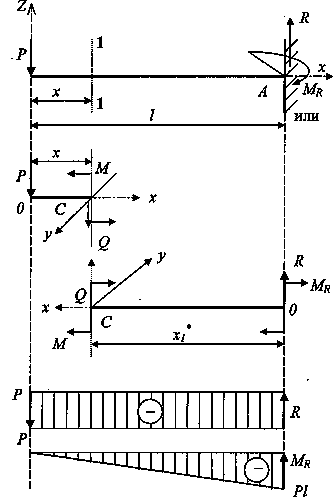
6.Типы
опор
а)
Шарнирно – неподвижная (двухсвязная)
опора: Воспринимает как вертикальные,
так и горизонтальные усилия (усилия под
углом).
б)
Шарнирно – подвижная опора – воспринимает
только вертикальные нагрузки. Реакция
опоры всегда направлена вдоль опорного
стержня, перпендикулярно опорной
поверхности
в)
Жесткая заделка (трехсвязная)
Реакции
в опорах определяют из условия равновесия
(уравнение статики).
7.Классификация
нагрузок
-
По
месту действия
Поверхностные
и объемные
а)
сосредоточенная сила
б)
распределенная сила
прямоугольная
Rq=
qa
треугольная
Rq=
½ qa
в)
сосредоточенный момент
изгибающий
скручивающий
г)
распределенный момент
Rmz=
mz a –равнодейств распр мом
-
По
времени действия
Постоянные
и временные
-
По
характеру действия
Статические
и динамические
-
По
характеру возникновения
Активная(известны)
и реактивная (неизвестны)
8.Основные
принципы изучаемого курса
При
расчете сложного сопротивления
используется принцип
независимости действия сил.
Сложный вид нагружения представляется
как система простых видов нагружения
действующих независимо друг от друга.
Решение при сложном сопротивлении
получается в результате сложения решений
полученных при простых видах нагружения.
принцип
Сен-Венана
на
достаточном удалении от места приложения
нагрузки характер её воздействия не
зависит от способа её приложения, а
зависит от величины равнодействующей.
9.Внутренние
усилия. Метод сечений (Метод РОЗУ)
Nz=∑z
(pi)
нормальная с
Qx=∑x
(pi)
поперечная с
Qy=∑y
(pi)
Mz=∑mz
(pi) крутящий
момент
Mx=∑mx
(pi) изгибающий
My=∑my
(pi)
Разрезаем
мысл тело плоск
Отбрасываем
одну из г внутр усил
Заменяем
внутр усилиями
Уравновешив
внутр ус внеш нагр
10.Правило
знаков внутренних усилий
Правило
знаков поперечных сил при изгибе:
Крутящий
момент
Против
ЧС при взгляде со стороны сеч то +
Правило
знаков изгибающих моментов:
Правило
проверки правильности построения эпюр
нагружения:
В
сечениях балки, где приложены внешние
сосредоточенные нагрузки на эпюре д.б.
скачёк на величину этой нагрузки.
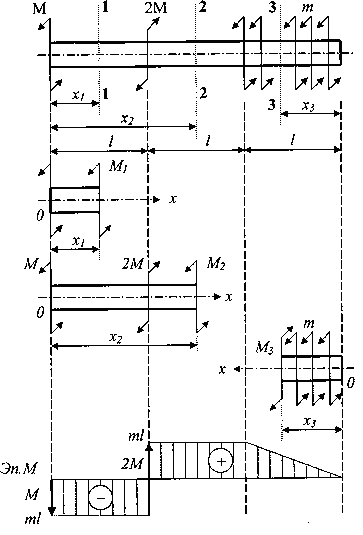
11.Эпюры
внутренних усилий
ПРИ
РАСТЯЖЕНИИ-СЖАТИИ
ПРИ
КРУЧЕНИИ
при
прямом изгибе
12.Дифференциальные
зависимости при изгибе
;
;
13.Следствия
из дифференциальных зависимостей
-
Если
на участке нет распр нагр (q=0)
то поперечная сила на этом участке
имеет пост вел., а эпюры изгиб мом
меняются по лин закону -
На
уч на котором присутст распр нагр пост
интенсивн. Поперечная сила меняется
по лин зак , а эпюры по закону квадр
параболы. Причем эпюра мх всегда напр
навстречу распр нагрузке. Где Qy равно
0 эпюра мх имеет экстремум. Если Qy равно
0 на всем участке, то мх постоян величину
4.
На участке где Qy>0 эпюра мх возрастает
слева направо
5.
В том сеч. где приложена сосред сила
эпюра Qy
имеет скачок на вел этой силы. В сеч где
сосред момент эпюра мх имеет скачок на
величену этого момента
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы найти осевой момент инерции прямоугольника относительно осей X и Y можно воспользоваться нашим онлайн калькулятором. Введите ширину и длину прямоугольника и всего за пару секунд получите значения моментов инерции.
Как рассчитать осевой момент инерции прямоугольника
Для расчёта моментов инерции прямоугольного сечения можно воспользоваться следующими формулами:
Ix = b * h3 / 12 — момент инерции прямоугольника относительно оси X,
Iy = h * b3 / 12 — момент инерции прямоугольника относительно оси Y, где
b — ширина прямоугольного сечения,
h — высота прямоугольного сечения.
Нахождение моментов инерции Yx и Yy часто необходимо в расчётах разных конструкций на прочность или устойчивость. Мы уверены что данный онлайн-калькулятор очень сильно облегчит вам вычисления.
Было полезно? Поделитесь с друзьями!
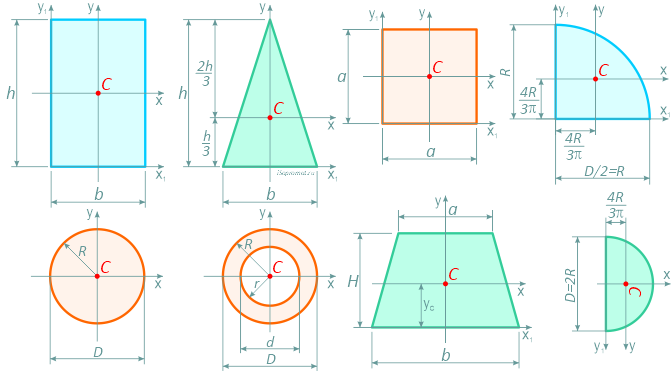
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
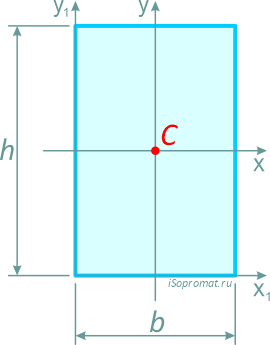
Прямоугольник
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
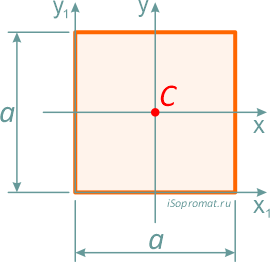
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
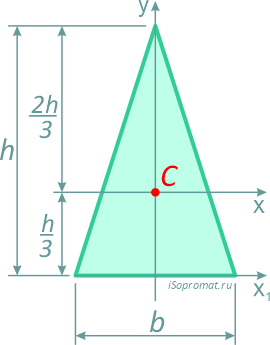
Треугольник равнобедренный
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
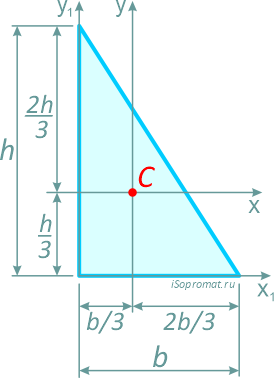
Прямоугольный треугольник
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
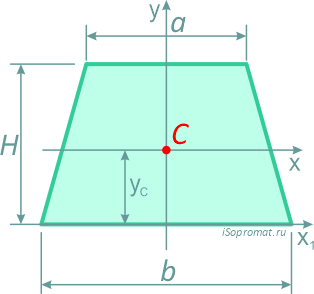
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
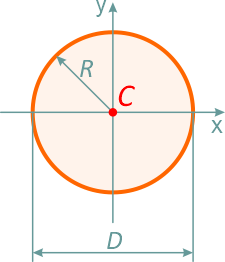
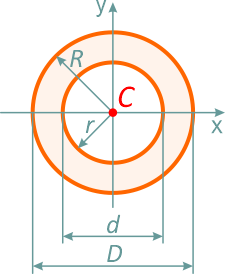
Круг
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
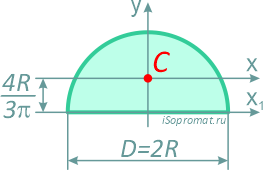
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
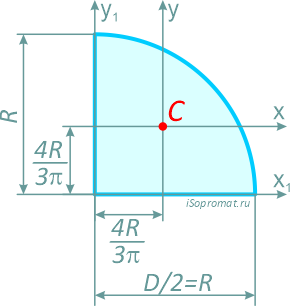
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
Кольцо
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
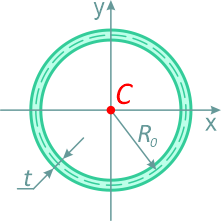
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
В прошлый раз мы поговорили о такой величине, как статические моменты. Теперь можем двигаться дальше: сегодня на повестке моменты инерции.
Внимательный читатель уже может возмутиться:
“И зачем мы изучаем эти моменты? Какой в этом прок?
Причём же тут инерция, если сопромат — по сути статика?»
На первый вопрос у меня есть два ответа — краткий и не очень. Пока ограничусь кратким:
Статические моменты и моменты инерции широко используются для определения нормальных и касательных напряжений, определении прогибов и деформаций конструкций. Читая о том, как все это вычислить, вы будете сталкиваться с геометрическими характеристиками постоянно. Поэтому лучше сразу понимать, о чем идёт речь, а, при необходимости, подсматривать тут.
В изгибаемом элементе от момента сил возникают напряжения, для определения которых нам и нужен момент инерции (хотя и опосредованно. Впрочем, если вы читали статью про моменты, то это уже знаете). При этом сам элемент деформируется, и величина этих деформаций (прогибов) также определяется с помощью момента инерции.
Для ответа на второй вопрос перейдем уже к моментам инерции.
Что такое момент инерции
Суть и смысл моментов инерции в общем случае походит на статические моменты, однако корни нужно искать в описании вращения тела. Для вращательного движения одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Рассмотрим вращающееся тело, как совокупность точек с предельно малыми размером и массой, которые находятся на расстояниях Ri (от нуля до R):
T — кинетическая энергия;
J — момент инерции;
m — масса;
v — скорость;
w — угловая скорость;
R — радиус;
Тут видно, что также, как в формуле кинетической энергии при линейном движении мера инертности — масса, при вращательном движении мера инертности — момент инерции. Впрочем, я немного забегаю вперёд.
Угловая скорость вращающегося тела — угол поворота, пройденный за единицу времени
Тут начальный угол поворота φ0 может быть равен нулю, если мы рассматриваем начало движения.
Линейная скорость тела:
Ускорение вращающегося тела (а нас интересует нормальное) тогда:
Я не буду затрагивать динамику вращающегося тела, и расскажу только о жизненно необходимом.
Сила (которая по второму закону Ньютона — произведение массы на ускорение):
и момент:
И вот тут вспомним уже третий закон Ньютона — действию всегда есть равное и противоположное противодействие, а значит действию найденного нами момента будет сопротивляться — момент инерции.
Вспомним также, что, как и со статическими моментами, на разные точки тела, удаленные от оси вращения на разные расстояния будет действовать разный момент, а общий момент можно получить их просуммировав:
При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. Но, как я уже показал, рассказывая про статические моменты, массу точек для изотропных (в данном случае имеющих одинаковую плотность) объектов можно выносить за скобки и рассматривать исключительно геометрию. Формула момента инерции примет следующий вид:
Почему Iр? Потому что мы с вами оперировали радиусом и углом поворота (в формуле угловой скорости) — т.е. использовали полярную систему отсчета (что и демонстрирует индекс p).
Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.
Как найти момент инерции
Чтобы немного упростить себе операции со всеми этими величинами перейдем к родной и понятной системе отсчета: перпендикулярным осям X и Y. Возьмем случайное сечение стержня и рассмотрим интегралы, как мы уже делали со статическими моментами:
Первые два интеграла называются осевыми моментами инерции относительно осей x и y, а третий — центробежным моментом инерции сечения относительно осей x, y. Теперь рассмотрим случай параллельного переноса осей , не вдаваясь глубоко в вычисление интегралов.
Для осей x1=x+a, y1=y+b моменты инерции будут равны:
Если вы, как и часть прочитавших эту статью перед публикацией, не имеете черного пояса и седьмого дана в интегральных преобразованиях, то:
т.к.
и
Тут первый интеграл — Ix1, второй интеграл — Sx1, а третий раскрывается в площадь при нулевом свободном члене.
Надеюсь, понятно, что при параллельном переносе по y изменяется только ось (буква).
В последнем случае мы рассматриваем перенос по обеим осям сразу.
Где:
Ix — очевидно, момент инерции относительно оси x
Sx — статический момент сечения относительно оси y
F — площадь сечения
А теперь предположим, что некие оси x1 и y1 являются центральными, тогда и выражения упрощаются и принимают вид:
Немного проясню обозначение осей:
Центральными называются оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.
Главными называются оси, в которых центробежный момент инерции (Ixy) равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.
И теперь можно уже коснуться практики: речь о моментах инерции простых сечений.
Момент инерции прямоугольника
Определим осевые моменты инерции прямоугольника со сторонами b и h относительно осей x и y, проходящих через его центр тяжести. В качестве элементарной площадки dA возьмем полоску шириной b и высотой . Тогда будем иметь:
Не прибегая к вычислениям, замечу, что для момента инерции относительно оси Y изменится только положение сторон b и h. Следовательно:
Момент инерции квадрата
Прямоугольник со сторонами b=h=a. Следовательно:
Момент инерции круга
Тут воспользуемся полярным моментом инерции относительно центра круга. Определим его, как сумму колец с толщиной dp:

Момент инерции кольца
А здесь – явная аналогия с моментом инерции круга:
Как мы видим, момент инерции кольца это разность моментов инерции большего и меньшего кругов.
Пример нахождения момента инерции тавра
Найдём осевые моменты инерции тавра (рисунок 5), приведенного на рисунке, относительно центральных осей xc и yc.
Рисунок 8. Тавр, положение осей
Так как оси x1 и x2 являются центральными осями для простых фигур в виде прямоугольников, для определения момента инерции фигуры относительно оси xc воспользуемся формулой.
Момент инерции относительно оси yc получим путем сложения моментов инерции простых фигур относительно этой же оси, так как ось yc является общей центральной осью для простых фигур и для всей фигуры.
Центробежный момент инерции относительно осей xc и yc равен нулю, так как ось инерции yc является главной осью (осью симметрии фигуры).
Обобщение и подведение итогов
Момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении. В статике момент инерции применяется в определении прогибов, расчетах конструкций на касательные и нормальные напряжения. Момент инерции также, как и статические моменты, характеризует положение осей относительно сечения элемента. Так у нас появляются:
Центральные оси, проходящие через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю.
Главные оси, в которых центробежный момент инерции (Ixy) равен нулю, а осевые моменты инерции — максимальны. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
При этом главные и центральные оси могут совпадать!
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников
5 448