Чтобы
получить согласие с результатами
наблюдений, Бор предположил,
что электрон в атоме водорода движется
только по
тем круговым орбитам, для которых его
момент импульса
М =
пħ,
n
= 1, 2, 3, …, (1.18)
где п
—
квантовые числа.
С
помощью этого правила
квантования можно
найти радиусы круговых
стационарных орбит водородоподобных
систем (Н, Не+,
Li++…)
и соответствующие им энергии. Пусть
заряд ядра водородоподобной
системы равен Ze.
Масса
ядра значительно больше массы
электрона, поэтому ядро при движении
электрона можно
считать неподвижным. Следуя Бору, будем
предполагать, что
электрон движется вокруг ядра по
окружности радиуса r.
Согласно
2-му закону Ньютона
(1.19)
где т
—масса
электрона. Отсюда кинетическая энергия
электрона
(1.20)
и
полная энергия электрона в кулоновском
поле ядра

Согласно
правилу квантования (1.18), rmV
=
nħ,
откуда
V=
nħ
/rm. (1.22)
После
подстановки (1.22) в (1.19) подучим выражение
для радиуса
n-й
стационарной орбиты:

Радиус
первой стационарной орбиты электрона
в атоме водорода
(п = 1, Z
= 1)
равен
rn
= ħ2
/те2
=
0,529·10-10
м. (1.24)
Его
называют боровским
радиусом.
Энергия
Еп
электрона
на n-й
стационарной орбите определяется
формулой (1.21), в которой под г
надо
понимать (1.23). И мы
приходим к следующему выражению для
Еп:

Эта
формула описывает уровни энергии
стационарных состояний
электрона в водородоподобной системе.
Для атома водорода
схема энергетических уровней,
соответствующих (1.25), показана на рис.
1.7. При п -><» уровни энергии сгущаются
к своему предельному значению Ек
=
0.
Состояние
атома с наименьшей энергией (п = 1) называют
основным.
Для
атома водорода основному состоянию
соответствует энергия Ei
= -13,53
эВ. Эта энергия (по модулю) является
энергией
связи электрона
в основном состоянии:
Есв
= Ei.
Именно
такую энергию надо
сообщить электрону в основном состоянии
(п = 1), чтобы удалить его из атома
водорода. По этой причине ее называют
еще и энергией
ионизации:
£ион
= Есв
= 13,6
эВ.
Это
значение, полученное из боровскои теории
атома, находится в хорошем согласии
с результатами эксперимента.
1.6. Магнитный момент атома водорода
Пусть
электрон движется
со скоростью v
по
орбите радиусом г (рис. 1.8). Через площадку,
пересекающую орбиту электрона, переносится
ежесекундно заряд ev,
где
е
—
заряд электрона, v
—
число оборотов электрона вокруг ядра
в
секунду. Следовательно, движущийся по
орбите
электрон образует круговой ток I
= ev.
Поскольку
заряд электрона отрицателен, направление
движения электрона противоположно
направлению
тока.
Магнитный
момент такого тока по
определению равен μ = IS,
или
μ =
ev·r2.
Учитывая,
что 2
rv
= V
и, перепишем предыдущее выражение
в
виде
.
Остается
учесть, что момент импульса электрона
М
=
rmv,
и
мы получим:

где
знак минус указывает, что направления
обоих моментов, μ и М, взаимно
противоположны.
Вектор
М называют орбитальным
моментом электрона.
Он образует с направлением движения
электрона правовинтовую систему (см.
рис. 1.8).
Отношение
магнитного момента частицы к ее
механическому моменту называют
гиромагнитным
отношением. Для
электрона оно равно
(1.34)
Воспользовавшись
воровским правилом квантования момента
импульса, т. е. формулой (1.18), перепишем
(1.33) в виде
μ = μБ
n
, п
= 1, 2,
3, …, (1.35)
где
μБ
— это так называемый магнетон
Бора:
μБ
= 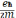
Дж/Т (1.36)
Таким
образом, при движении электрона по
первой воровской орбите (п = 1) его
магнитный момент равен одному магнетону
Бора. В дальнейшем мы увидим, что это
резко расходится с экспериментом,
значит, полученный результат оказывается
совершенно неверным. И тем не менее, мы
привели формулы, связывающие магнитный
момент с механическим, поскольку они
послужат основой для получения правильных
результатов .
Недостатки
теории Бора. Теория
Бора явилась крупным шагом в развитии
теории атома, в понимании новых квантовых
закономерностей, с которыми столкнулась
физика при изучении явлений микромира.
Эта теория отчетливо показала
неприменимость законов классической
физики для описания внутриатомных
явлений
Теория
Бора стимулировала постановку многих
экспериментов, принесших важные
результаты. Даже в тех многочисленных
случаях, когда теория не могла дать
количественное объяснение явлений,
два постулата Бора служили руководящей
нитью при классификации и количественной
интерпретации этих явлений.
Однако
двух постулатов Бора недостаточно для
построения полной теории. Они должны
быть дополнены правилами
квантования. Эти
правила, достаточно искусственно
введенные Бором для одноэлектронного
атома, радикально проблемы не решили.
Их не удалось распространить даже на
простейший после водорода атом гелия,
содержащий два электрона. Кроме того,
теория Бора позволила вычислить только
частоты спектральных линий, но не их
интенсивность.
Основной
же, принципиальный недостаток теории
Бора — это ее непоследовательность:
она
не была ни последовательно классической,
ни последовательно квантовой. Эта теория
принимала существование стационарных
состояний атома, что совершенно
непонятно с точки зрения классической
физики. И вместе с тем к движению
электронов в стационарных состояниях
она применяла законы классической
механики, хотя и считала неприменимой
классическую электродинамику (поскольку
нет излучения).
Итак,
планетарную модель атома нельзя считать
серьезной теорией. Она просто неверна.
Тот факт, что эта модель приводит к очень
хорошим результатам в случае атома
водорода (при расчете некоторых величин),
по существу случайный. Этот успех явился
мощным толчком к развитию квантовой
теории атома. Сам Бор рассматривал свою
теорию как промежуточный этап в поисках
верной теория. Такой последовательной
теорией явилась квантовая физика.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Цитировать:
Лякишев В.К. РАСЧЁТ ДИАМЕТРА МОЛЕКУЛЫ ВОДОРОДА В РАМКАХ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ // Universum: химия и биология : электрон. научн. журн. 2023. 2(104). URL: https://7universum.com/ru/nature/archive/item/14860 (дата обращения: 25.05.2023).
АННОТАЦИЯ
Данная работа относится к области физической химии. При помощи формул электрической ёмкости и электрической энергии сферического конденсатора из классической электродинамики в работе рассчитан диаметр молекулы водорода, форма которой близка к сферической. Также в ходе вычислений были использованы энергия Хартри (абсолютное значение электрической потенциальной энергии атома водорода) и энергия диссоциации молекулы водорода. Полученный в работе диаметр молекулы водорода (1,8 Å) близок к так называемому кинетическому диаметру, определённому через длину свободного пробега молекулы (2,3 Å).
ABSTRACT
This work is related to the field of physical chemistry. Using formulas of electric capacity and electric energy of spherical capacitor from classical electrodynamics, the diameter of hydrogen molecule whose shape is almost spherical has been calculated. The Hartree energy (the absolute value of the hydrogen atom electric potential energy) and the hydrogen molecule dissociation energy have been taken into account in the calculations as well. The hydrogen molecule diameter obtained in the work (1,8 Å) is a close to the so-called kinetic diameter, defined through mean free path of the molecule (2,3 Å).
Ключевые слова: молекула водорода, эффективный диаметр, энергия Хартри, энергия диссоциации молекулы, ёмкость сферического конденсатора, энергия конденсатора, теорема вириала, длина свободного пробега молекулы.
Keywords: molecular hydrogen, effective molecular diameter, Hartree energy, bond-dissociation energy, capacity of a spherical capacitor, capacitor energy, virial theorem, mean free path.
Введение
Молекула водорода является простейшей двухатомной молекулой с ковалентной неполярной химической связью [2]. Достаточно точно вычислены среднее межъядерное расстояние в молекуле водорода [9], а также энергия диссоциации молекулы [6] (то есть энергия, необходимая для диссоциации одной молекулы, не находящейся во взаимодействии с другими молекулами). Однако размеры молекулы водорода известны недостаточно точно. Эффективный диаметр молекулы водорода принято оценивать по длине свободного пробега молекулы [1] (расстоянию, которое пролетает молекула между двумя последовательными столкновениями).
Средняя длина свободного пробега молекулы водорода определяется по формуле:
/Lyakishev.files/image001.png)
где n – концентрация молекул водорода, которую можно определить из уравнения Менделеева-Клапейрона:
/Lyakishev.files/image003.png)
(p – давление водорода, равное 105 Па; T – температура водорода по абсолютной шкале, равная 273 К; k = 1,38 · 10-23 Дж/К — постоянная Больцмана).
Подставив концентрацию молекул водорода в формулу средней длины свободного пробега молекулы водорода, можно найти диаметр молекулы:
/Lyakishev.files/image004.png)
При длине свободного пробега /Lyakishev.files/image005.png)
Целью данной работы является расчёт эффективного диаметра молекулы водорода принципиально новым способом.
Метод состоит в использовании положений квантовой физики (энергия Хартри), теоретической физики (теорема вириала), экспериментальной химии (энергия диссоциации молекулы водорода), классической физики (электрическая энергия и ёмкость конденсатора), Евклидовой геометрии (обоснованное приближение формы молекулы водорода сферой).
Расчет эффективного диаметра молекулы водорода
/Lyakishev.files/image006.png)
/Lyakishev.files/image007.png)
Тогда модуль полной энергии молекулы водорода будет складываться из двух полных энергий атома водорода (их абсолютных значений) и энергии диссоциации молекулы водорода:
/Lyakishev.files/image008.png)
где /Lyakishev.files/image009.png)
По теореме о вириале потенциальная энергия молекулы водорода равна удвоенной полной энергии молекулы водорода:
/Lyakishev.files/image010.png)
Отношение потенциальных энергий молекулы водорода и атома водорода будет равно:
/Lyakishev.files/image011.png)
С другой стороны, атом водорода и молекулу водорода можно представить в виде сферических конденсаторов. Равновесное межатомное расстояние в молекуле водорода, равное 0,74 Å, превышает боровский радиус, равный 0,53 Å. Это означает глубокое перекрытие электронных облаков атома. Поэтому форма граничной поверхности общего электронного облака молекулы близка к сферической. Используя формулы энергии заряженного сферического конденсатора [3] и электрической ёмкости сферического конденсатора [7], запишем потенциальные энергии для атома и молекулы водорода в виде:
/Lyakishev.files/image012.png)
где e – заряд электрона, /Lyakishev.files/image013.png)
/Lyakishev.files/image014.png)
/Lyakishev.files/image015.png)
/Lyakishev.files/image016.png)
Подставив электрическую ёмкость атома водорода в формулу потенциальной энергии атома водорода, получим:
/Lyakishev.files/image017.png)
Потенциальная энергия молекулы водорода будет равна:
/Lyakishev.files/image018.png)
где e – заряд электрона, /Lyakishev.files/image019.png)
/Lyakishev.files/image020.png)
(d – эффективный диаметр молекулы водорода).
Подставив электрическую ёмкость молекулы водорода в формулу потенциальной энергии молекулы водорода, получим:
/Lyakishev.files/image021.png)
Найдём отношение потенциальных энергий молекулы водорода и атома водорода:
/Lyakishev.files/image022.png)
Тогда эффективный диаметр молекулы водорода равен:
/Lyakishev.files/image023.png)
Полученное значение диаметра молекулы водорода близко к значению, вычисленному по формуле (3), а полученное значение полной энергии молекулы очень близко к значениям, полученными другими методами [5].
Заключение
Молекула водорода является квантово-механической системой, однако нелинейные эффекты квантовой электродинамики существенны на маленьких расстояниях, сравнимых с комптоновской длиной волны электрона. Поэтому в работе был проведён расчёт диаметра молекулы водорода с использованием методов классической электродинамики. Это позволило получить результат, близкий к общепринятому, что подтверждает корректность применённых методов.
Список литературы:
- Алешкевич В.А. Курс общей физики. Молекулярная физика. – М. : Физматлит, 2016. – С. 281–283.
- Барковский Е.В., Ткачев С.В., Петрушенко Л.Г. Общая химия. – Минск : Вышэйшая школа, 2013. – С. 58.
- Бобрович О.Г., Тульев В.В. Физика в 5 ч. Ч. 2. Электростатика. Постоянный электрический ток. – Минск : БГТУ, 2011. – С. 57.
- Ермаков А.И. Квантовая механика и квантовая химия. Ч. 2. Квантовая химия : учебник и практикум для вузов. – М. : Юрайт, 2022. – С. 14.
- Институт теоретической химии / [Электронный ресурс]. – Режим доступа: http://itchem.ru/energiya_molekuly_vodoroda.
- Никольский Б.П., Рабинович В.А. Справочник химика. Т. 1. Общие сведения. Строение вещества. Свойства важнейших веществ. Лабораторная техника. – М. –Л. : Химия, 1966. – С. 338.
- Савельев И.В. Курс общей физики. Т. 2. Электричество и магнетизм. Волны. Оптика : учеб. пособие. – М. : Наука, Главная редакция физико-математической литературы, 1982. – С. 93.
- Сивухин Д.В. Общий курс физики. Т. 1. Механика. – М. : Физматлит, 2005. – C. 148.
- Стась Н.Ф. Справочник по общей и неорганической химии : учеб. пособие. – Томск : Изд-во Томского политехнического университета, 2011. – С. 26.
- URL: https://physics.nist.gov/cgi-bin/cuu/Value?bohrrada0.
- URL: https://physics.nist.gov/cgi-bin/cuu/Value?hrev.
- WolframAlpha / [Электронный ресурс]. – Режим доступа: https://www.wolframalpha.com/input/?i=Hartree.
Атом водорода — физическая система, состоящая из атомного ядра, несущего элементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å.
Атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике, поскольку для него проблема двух тел имеет точное или приближенное аналитическое решения. Эти решения применимы для разных изотопов водорода, с соответствующей коррекцией.
В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощенно рассматривается как электрон в электростатическом поле бесконечно тяжёлого атомного ядра, не участвующего в движении (или просто в кулоновском электростатическом потенциале вида 1/r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.
В 1913 году Нильс Бор предложил модель атома водорода, имеющую множество предположений и упрощений, и вывел из неё спектр излучения водорода. Предположения модели не были полностью правильны, но тем не менее приводили к верным значениям энергетических уровней атома.
Результаты расчётов Бора были подтверждены в 1925—1926 годах строгим квантово-механическим анализом, основанном на уравнении Шрёдингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра выводится в аналитической форме. Оно описывает не только уровни энергии электрона и спектр излучения, но и форму атомных орбиталей.
Содержание
- 1 Решение уравнения Шрёдингера
- 2 Математическое описание атома водорода
- 2.1 Энергетический спектр
- 2.2 Волновые функции
- 2.3 Угловой момент
- 3 Нахождение энергии электрона из модели Бора
- 4 Визуализация орбиталей атома водорода
- 5 Строение и свойства атома водорода
- 5.1 Образование атома водорода и его спектр излучения
- 5.2 Возбуждение и ионизация атома водорода
- 5.3 Строение атома водорода в основном состоянии
- 5.4 Атом водорода в электрическом поле
- 5.5 Взаимодействие атома водорода с протоном
- 5.6 Взаимодействие атома водорода с электроном
- 5.7 Рекомбинация атомов водорода
- 6 Примечания
- 7 См. также
- 8 Ссылки
Решение уравнения Шрёдингера
Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами, обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны, их зависимость от угловой координаты следуют полностью из изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, …, +l; оно определяет проекцию углового момента на (произвольно выбранную) ось z.
В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента, нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1/r радиальные волновые функции записываются с использованием полиномов Лагерра). Это приводит к третьему квантовому числу, которое называется основным квантовым числом n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничено основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.
Из-за сохранения углового момента состояния с одинаковыми l, но различными m в отсутствие магнитного поля имеют одну и ту же энергию (это выполняется для всех задач с аксиальной симметрией). Кроме того, для водородного атома состояния с одинаковыми n, но разными l также вырождены (то есть имеют одинаковую энергию). Однако это свойство — особенность лишь атома водорода (и водородоподобных атомов), оно не выполняется для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).
Если мы примем во внимание спин электрона, то появится последнее, четвёртое квантовое число, определяющее состояния атома водорода — проекция углового момента собственного вращения электрона на ось Z. Эта проекция может принимать два значения. Любое собственное состояние электрона в водородном атоме полностью описывается четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и 

Рассмотрим сейчас решение уравнения Шрёдингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид 
Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, 


Уравнение Шрёдингера в сферических координатах:
В этом уравнении 




После подстановки значений частных производных в уравнение Шрёдингера получим:
Умножим уравнение на
Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.
Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим её 
Решением этого уравнения являются функции
Угол φ может изменяться от 0 до 2π. Функция 


Далее, интегрируя квадрат модуля функции 
Далее рассмотрим левую часть уравнения (1). Она, конечно, равна
Разделим уравнение на
После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через 
Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.
Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален 

Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).
Магнитное квантовое число 
Математическое описание атома водорода
Энергетический спектр
Энергетические уровни атома водорода, включая подуровни тонкой структуры, записываются в виде
-
- где
— постоянная тонкой структуры,
— собственное значение оператора полного момента импульса.
Энергию 

-
(в системе СИ),
где h — постоянная Планка, 
Волновые функции
В сферических координатах волновые функции имеют вид:
где:
— Боровский радиус.
— обобщённые полиномы Лагерра степени
от функции
— нормированные на единицу сферические функции.
Угловой момент
Собственные значения для оператора углового момента:
Нахождение энергии электрона из модели Бора
Вычислим уровни энергии атома водорода без учёта тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения 

Здесь 



Отсюда кинетическая энергия электрона
где 
Потенциальная его энергия
Полная энергия, соответственно, равна
Для нахождения радиуса rn стационарной орбиты с номером n рассмотрим систему уравнений, в которой второе уравнение есть математическое выражение первого постулата Бора
Отсюда получаем выражение для радиуса стационарной орбиты с номером n:
Радиус первой орбиты оказывается равным 
Подставляя это значение в выражение для энергии, получим, что
Отсюда мы можем найти волновое число (по определению это обратная длина волны или число длин волн, укладывающихся на 1 см) фотона, излучаемого атомом водорода за один переход из возбужденного состояния с главным квантовым числом 
где 
Визуализация орбиталей атома водорода
Плотность вероятности для электрона при различных квантовых числах (l)
Изображение справа показывает первые несколько орбиталей атома водорода (собственные функции гамильтониана). Они представляют собой поперечные сечения плотности вероятности, величина которой отражена цветом (чёрный цвет соответствует минимальной плотности вероятности а белый — максимальной). Квантовое число углового момента l обозначено в каждой колонке, используя обычные спектроскопические обозначения (s означает l = 0; p: l = 1; d: l = 2). Главное квантовое число n (= 1, 2, 3…) отмечено справа от каждого ряда. Для всех картин магнитное квантовое число m равно 0, и сечение взято в плоскости — XZ, Z — вертикальная ось. Плотность вероятности в трёхмерном пространстве получается при вращении картинки вокруг оси Z.
Основное состояние, то есть состояние самой низкой энергии, в котором обычно находится электрон, является первым, состоянием 1s (n = 1, l = 0). Изображение с большим количеством орбиталей доступно до более высоких чисел n и l. Отметим наличие чёрных линий, которые появляются на каждой картинке, за исключением первой. Они — узловые линии (которые являются фактически узловыми поверхностями в трёх измерениях). Их общее количество всегда равно n − 1, которое является суммой числа радиальных узлов (равного n − l − 1) и числа угловых узлов (равного l).
Строение и свойства атома водорода
Образование атома водорода и его спектр излучения
При попадании в электрическое поле положительно заряженного протона отрицательно заряженного электрона происходит захват последнего протоном — образуется атом водорода. Образовавшийся атом водорода находится в возбуждённом состоянии. Время жизни атома водорода в возбуждённом состоянии — ничтожные доли секунды (10−8 — 10−10сек)[1], однако очень высоковозбуждённые атомы в бесстолкновительной среде могут существовать до секунд. Снятие возбуждения атома происходит за счёт излучения фотонов с фиксированной энергией, проявляющихся в характерном спектре излучения водорода. Поскольку газообразный атомарный водород содержит множество атомов в различных степенях возбуждения, спектр состоит из большого числа линий.
Схема происхождения спектра атомарного водорода представлена на рисунке.[2].
Линии спектра серии Лаймана обусловлены переходом электронов на нижний уровень с квантовым числом n = 1 с уровней с квантовыми числами n = 2, 3, 4, 5, 6… Линии Лаймана лежат в ультрафиолетовой области спектра. Линии спектра серии Бальмера обусловлены переходом электронов на уровень с квантовым числом n = 2 с уровней с квантовыми числами n = 3, 4, 5, 6… и лежат в видимой области спектра.
Линии спектра серий Пашена, Брэкета и Пфунда обусловлены переходом электронов на уровни с квантовыми числами n, равными 3, 4 и 5 (соответственно), и расположены в инфракрасной области спектра.[3].
В нормальном (основном) состоянии (главное квантовое число n = 1) атом водорода в изолированном виде может существовать неограниченное время. Согласно квантохимическим расчетам, радиус мест наибольшей вероятности нахождения электрона в атоме водорода в нормальном состоянии (главное квантовое число n = 1) равен 0,529 Å. Этот радиус является одной из основных атомных констант, он получил название боровский радиус (см. выше). При возбуждении атома водорода электрон проходит на более высокий квантовый уровень (n = 2, 3, 4 и т. д.), при этом радиус мест наибольшей вероятности нахождения электрона в атоме возрастает пропорционально квадрату главного квантового числа:
- rn = a0 · n2.
Возбуждение и ионизация атома водорода
Уровни энергии атома водорода.
Возбуждение атома водорода происходит при нагревании, электроразряде, поглощении света и т. д., причём в любом случае атом водорода поглощает определённые порции — кванты энергии, соответствующие разности энергетических уровней электронов. Обратный переход электрона сопровождается выделением точно такой же порции энергии. Квантовые переходы электрона соответствуют скачкообразному изменению концентрического шарового слоя вокруг ядра атома водорода, в котором преимущественно находится электрон (шаровым слой является только при нулевом значении азимутального квантового числа l).
Согласно квантовомеханическим расчётам, наиболее вероятное расстояние электрона от ядра в атоме водорода равно боровскому радиусу ~ 0,53 Å при n = 1; 2,12 Å — при n = 2; 4,77 Å — при n = 3 и так далее. Значения этих радиусов относятся как квадраты натуральных чисел (главного квантового числа) 12 : 22 : 32…. В очень разреженных средах (например, в межзвёздной среде) наблюдаются атомы водорода с главными квантовыми числами до 1000 (ридберговские атомы), чьи радиусы достигают сотых долей миллиметра.
Если электрону в основном состоянии придать дополнительную энергию, превышающую энергию связи E0 ≈ 13,6 эВ, происходит ионизация атома водорода — распад атома на протон и электрон.
Радиальное распределение вероятности нахождения электрона в атоме.
Строение атома водорода в основном состоянии
Радиальная зависимость dp(r)/dr плотности вероятности нахождения электрона в атоме водорода, находящемся в основном состоянии, представлена на рисунке. Эта зависимость даёт вероятность того, что электрон будет обнаружен в тонком шаровом слое радиуса r толщиной dr с центром в ядре. Площадь этого слоя равна S = 4πr2, его объём dV = 4πr2dr. Общая вероятность нахождения электрона в слое равна (4πr2dr) ψ2, поскольку в основном состоянии волновая функция электрона сферически симметрична (то есть постоянна в рассматриваемом шаровом слое). Рисунок выражает зависимость dp(r)/dr = 4πr2ψ2. Кривая радиального распределения плотности вероятности dp(r)/dr нахождения электрона в атоме водорода имеет максимум при a0. Этот наиболее вероятный радиус совпадает с боровским радиусом. Размытое облако плотности вероятности, полученное при квантовомеханическом рассмотрении, значительно отличается от результатов теории Бора и согласуется с принципом неопределённости Гейзенберга. Это размытое сферически симметричное распределение плотности вероятности нахождения электрона, называемое электронной оболочкой, экранирует ядро и делает физическую систему протон-электрон электронейтральной и сферически симметричной — у атома водорода в основном состоянии отсутствуют электрический и магнитный дипольные моменты (как и моменты более высоких порядков), если пренебречь спинами электрона и ядра. Следует отметить, что максимум объёмной плотности вероятности ψ2 достигается не при r = a0, как для радиальной зависимости, а при r = 0.
Атом водорода в электрическом поле
По теории деформационной поляризации, нейтральный атом водорода, попадая во внешнее электрическое поле, подвергается деформации — центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L, что приводит к появлению в атоме водорода наведённого электрического дипольного момента μ[4]. Величина наведённого дипольного момента прямо пропорциональна напряжённости внешнего электрического поля E:
- μ = αeE = Lq.
Коэффициент пропорциональности αe носит название электронной поляризуемости. Электронная поляризуемость атома водорода составляет 0,66 Å3.[5]
Чем выше напряжённость приложенного электрического поля, тем больше смещение центра электронной оболочки от центра атома водорода и, собственно, длина наведённого диполя
- L = αe E/q,
где q — величина заряда ядра атома водорода.
При высоких значениях напряжённости приложенного электрического поля атом водорода подвергается ионизации полем с образованием свободных протона и электрона.
Взаимодействие атома водорода с протоном
Деформационная поляризация атома водорода в электрическом поле протона
Протон, обладая положительным элементарным электрическим зарядом q = 1,602•10 −19 Кл, как и всякий точечный электрический заряд создаёт вокруг себя электрическое поле с напряжённостью E. E = q/R2, Где R — расстояние точки поля до протона.
Нейтральный атом водорода, попадая в электрическое поле протона, подвергается деформационной поляризации (рис.1.). Длина наведённого электрического диполя атома водорода обратно пропорциональна квадрату расстояния между атомом водорода и протоном L = αe E/q = αe/R2 = 0,66/R2
Отрицательный полюс наведённого электрического диполя атома водорода ориентируется в сторону протона. В результате чего начинает проявляться электростатическое притяжение между атомом водорода и протоном. Сближение частиц (атома водорода и протона) возможно до тех пор, пока центр плотности вероятности нахождения электрона станет равноудалённым от обоих протонов. В этом предельном случае d=R=2L. Центр области вероятного нахождения электрона совпадает с центром симметрии образовавшейся системы H2+ — молекулярного иона водорода, при этом d=R=2L=³√2αe = ³√2•0,66 = 1,097 Å.
Найденная величина d = 1,097 Å близка к экспериментальной величине межъядерного расстояния в молекулярном ионе водорода H2+ — 1,06 Å.[6]
Взаимодействуя с протоном, атом водорода образует молекулярный ион водорода
H2+,H + H + -> H2+ + Q,
Характеризующийся простейшей одноэлектронной ковалентной химической связью.
Взаимодействие атома водорода с электроном
Рис. Деформационная поляризация атома водорода под действием приближающегося электрона и модель гидрид-иона H—
Электрон, обладая элементарным электрическим зарядом, как и протон создаёт вокруг себя электрическое поле, но в отличие от электрического поля протона с отрицательным знаком. Нейтральный атом водорода, попадая в электрическое поле электрона подвергается деформационной поляризации. Центр электронной оболочки атома водорода смещается относительно ядра на некоторое расстояние L в противоположную сторону к приближающемуся электрону. Приближающийся электрон как бы вытесняет из атома водорода находящийся в нём электрон, подготавливая место для второго электрона. Величина смещения центра электронной оболочки атома водорода L обратно пропорциональна квадрату расстояния атома водорода к приближающемуся электрону R:
L = αe/R2 = 0.66/R2 (рис)
Сближение атома водорода и электрона возможно до тех пор, пока центры областей плотностей вероятности нахождения обоих электронов не станут равноудалёнными от ядра объединённой системы — отрицательно заряженного иона водорода. Такое состояние системы имеет место при:
re = L = R = 3√0,66 = 0,871 Å.
Где re — орбитальный радиус двухэлектронной оболочки гидрид-иона H—.
Таким образом, атом водорода проявляет своеобразную амфотерность, он может взаимодействовать как с положительно заряженной частицей (протоном), образуя молекулярный ион водорода H2+, так и с отрицательно заряженной частицей (электроном), образуя гидрид-ион H—.
Рекомбинация атомов водорода
Рекомбинация атомов водорода обсуловлена силами межатомного взаимодействия. Происхождение сил, вызывающих притяжение электрически нейтральных атомов друг к другу, было объяснено в 1930 году Ф.Лондоном. Межатомное притяжение возникает вследствие флуктуации электрических зарядов в двух атомах, находящихся близко друг от друга. Поскольку электроны в атомах движутся, то каждый атом обладает мгновенным электрическим дипольным моментом, отличным от нуля. Мгновенный диполь (электродинамика) на одном атоме наводит противоположно направленный диполь в соседнем атоме. Наступает синхронизация колебаний двух атомов — двух осцилляторов, частоты которых совпадают. Результатом этого процесса является образование молекулы водорода.
Наличие мгновенного электрического дипольного момента у атома водорода выражается в характерной особенности атома водорода, проявляющейся в крайней реакционной способности атомарного водорода и склонности его к рекомбинации. Время существования атомного водорода составляет около 1 сек. Под давлением в 0.2 мм рт. ст. Рекомбинация атомов водорода имеет место, если образующаяся молекула водорода быстро освобождается от избытка энергии, выделяющейся при взаимодействии атомов водорода путём тройного столкновения. Соединение атомов водорода в молекулу протекает значительно быстрее на поверхности различных металлов, чем в самом газе. При этом металл воспринимает ту энергию, которая выделяется при образовании молекул водорода, и нагревается до очень высоких температур. Тепловой эффект реакции образования молекулярного водорода из атомов водорода составляет 103 ккал/моль.
На принципе рекомбинации атомов водорода разработана атомно-водородная сварка. Между двумя вольфрамовыми стержнями создаётся электрическая дуга, через которую по облегчающим стержни трубкам пропускается ток водорода. При этом часть молекул водорода распадается на атомы, которые затем вновь соединяются на металлической поверхности, помещаемой на небольшом расстоянии от дуги. Металл может быть таким путём нагрет до температуры выше 3500° C[7].
Константы реакции диссоциации молекулярного водорода (Kp) и степень превращения водорода в атомарное состояние (α) в зависимости от абсолютной температуры (T) представлены в таблице[8]:
| T, к | 2000 | 3000 | 4000 | 5000 | 6000 | 8000 |
|---|---|---|---|---|---|---|
| Кр | 2,62 · 10-6 | 2,47 · 10-2 | 2,52 | 4,09 · 10 | 2,62 · 102 | 2,70 · 103 |
| α | 8,10 · 10-4 | 7,83 · 10-2 | 0,621 | 0,954 | 0,992 | 0,999 |
Примечания
- ↑ Ахметов Н. С. Неорганическая химия. Учебное пособие для вузов с ил. — 2-е изд., перераб. и доп. — М.: «Высшая школа», 1975. — 672 с.
- ↑ Некрасов Б. В. Курс общей химии. — 14-е изд. — М.: ГНТИ химической литературы, 1962. — С. 113. — 976 с.
- ↑ Даниэльс Ф., Олберти Р. Физическая химия. — пер. с англ. под ред. д. х. н., проф. К. В. Топчиевой. — М.: «Мир», 1978. — С. 369-370. — 645 с.
- ↑ Потапов А. А. Деформационная поляризация: Поиск оптимальных моделей. — Новосибирск: «Наука», 2004. — 511 с. — ISBN 5-02-032065-X
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: Издательство химической литературы, 1962. — Т. 1. — С. 385. — 1071 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: Издательство химической литературы, 1962. — Т. 1. — С. 388. — 1071 с.
- ↑ Некрасов Б. В. Курс общей химии. — 14-е изд. — М.: ГНТИ химической литературы, 1962. — С. 110. — 976 с.
- ↑ Справочник химика. — 2-е изд., перераб. и доп. — Л.-М.: «Химия», 1964. — Т. 3. — С. 24. — 1008 с. — 65 000 экз.
См. также
- Водород
- Водородоподобный атом
- Квантовая механика
- Квантовая химия
- Квантовая теория поля
- Квантовое состояние
- Принцип неопределённости
- Волновая функция
- Электронное облако
- Ридберговский атом
Ссылки
- Griffiths David J. Introduction to Quantum Mechanics. — Upper Saddle River, NJ: Prentice Hall, 1995. — ISBN ISBN 0-13-111892-7
Параграф 4.2 описывает атом водорода, а вся глава 4 имеет отношение к теме.
- Bransden B.H. Physics of Atoms and Molecules. — London: Longman, 1983. — ISBN ISBN 0-582-44401-2
- Физика атома водорода на Scienceworld
- Графическое представление орбиталей
- Апплет изображающий орбитали атома водорода
- Японские ученые сфотографировали атом водорода\ИТАР-ТАСС
ru:Протий
Линейная скорость жидкости, рассчитанная по приведенным в патенте примерам, составляла 4— см/мин. Величина линейной скорости невелика, и устойчивый транспортный режим для катализатора обеспечивается, очевидно, за счет малого размера его частиц, небольшой плотности катализатора [обусловленной низким содержанием металлов —24% (масс.)], высокой концентрации углевода в растворе и, следовательно, большой его вязкости, а также большого модуля водорода. [c.103]
При проведении гидрогеиолиза углеводов в колонном реакторе с суспендированным катализатором важным технологическим параметром становится модуль водорода, т. е. соотношение объемов компримированного водорода и сырья. Введение газа в значительной степени снижает линейную скорость жидкости, соответствую-дую скорости уноса катализатора [20, 62], однако достаточно точ- [c.125]
В реакторе интенсивного перемешивания величина модуля водорода не является столь критической более того, слишком большой модуль газа может даже снизить интенсивность перемешивания. Однако в проточных условиях и в этом случае необходим некоторый минимальный избыток водорода сверх потребляемого для реакции и растворимого в жидкости. Роль его состоит в удалении выделяющихся побочных газообразных продуктов (метан, углекислый газ и др.) без существенного снижения парциального давления водорода. Величина модуля избыточного водорода может в этом случае колебаться от очень малой (0,25) [23] до значительной (4—5), в зависимости от конструкции реактора и других факторов, и должна определяться при экспериментальной оптимизации процесса известными методами [35]. [c.126]
Следует вновь подчеркнуть, что полученное описание адекватно только в исследованной области, т. е. при 215—235 °С, концентрациях катализатора 8—16%, давлениях водорода 8—15 МПа, расходах сырья 2—3 ч (при времени контакта 20—30 мин), модуле водорода 0,2—1,0 и т. д. [c.134]
Выход остаточной глюкозы Е4. Этот параметр, естественно, уменьшается с увеличением давления водорода, уменьшением концентрации глюкозы в сырье, а при высокой ее концентрации — с увеличением температуры. Одновременное увеличение концентраций Са(0Н)2 и хлорного железа также снижает выход E . Снижается он и при увеличении концентрации катализатора и увеличении модуля водорода. Время контакта (в пределах 20—30 мин) на выход 4 не влияет. [c.135]
Модуль водорода X в определенных пределах целесообразно увеличивать. [c.136]
В заключение следует заметить, что аппаратурное оформление процесса гидрогеиолиза должно позволять варьировать его параметры в сравнительно широких пределах температуру в реакторах— за счет создания запаса поверхностей нагрева, время контакта — путем применения дозировочных насосов с регулируемой производительностью, модуль водорода — созданием запасов мощности компрессора и поверхностей подогревателей водорода и т. д. В этом случае оптимизация процесса гидрогеиолиза не представит особых трудностей, и задачу можно переложить на управляющую вычислительную машину (при условии разработки надежного математического описания промышленного процесса). [c.142]
Процесс гидрирования проводится при 10—12-кратном избытке водорода по отношению к объему гидрируемой жидкости. Для поддержания требуемого модуля водорода проводят его циркуляцию в системе при помощи циркуляционных газовых насосов. Применяемый технический водород должен содержать не менее 99,6% водорода. В случае загрязнения водорода примесями кислорода и других газов предусматривается возможность сброса водорода в атмосферу. [c.156]
В работах голландских исследователей [16] проведено сравнение процессов гидрогеиолиза сахарозы в оборудовании периодического действия (в автоклавном режиме) и на непрерывно действующей установке. Последняя представляла собой каскад из двух реакторов с полезным объемом 250 см каждый реакторы были снабжены тремя отражательными перегородками и турбинной мешалкой с четырьмя лопастями, делающей 1400 об/мин. Температура в первом реакторе была 225 °С, во втором — 200 °С, давление водорода составляло 20 МПа, объемная скорость сырья 1 ч 1, модуль водорода 2,5. Сахарозу подвергали гидрогенолизу в виде 9%-ного раствора в смеси метанол — вода (75—25 по массе) с добавлением 2% Са(0Н)2 (к углеводу) в присутствии медно-це-риевого катализатора на окиси кремния (95 частей СиО 5 частей СеОгГ 100 частей SiOj). [c.105]
Растворимость водорода в воде при давлении 15 МПа составляет всего 2,681 смУсм при 100 °С [38], а при 200—225 °С еще меньше (порядка 2 смУсм воды). Кроме того, при высоких температурах объем жидкой фазы в реакторе уменьшается, так как часть воды испаряется, особенно при больших модулях водорода и при значительных давлениях, когда существенным становится явление фугитивности. Растворимость водорода в 10— 15%-ных растворах углеводов и полиолов практически такая же, как в чистой воде [38]. По приблизительной оценке количество водорода, потребляемого при гидрогенолизе, на 2 порядка выше, чем может единовременно раствориться в сырьевой суспензии. Поэтому [c.115]
На заводе в Хёхсте линейная скорость водорода в 10 раз превышала скорость суспензии патенты Атлас Кемикл Ко предусматривали вдвое больший модуль водорода. На опытной установке [c.126]
Выход глицерина Наибольшее положительное влияние на 1 оказывает модуль водорода вероятно, увеличение расхода водорода усиливает его диспергирование в данной реакционной системе. Следующим по силе является влияние взаимодействия температуры реакции и концентрации катализатора знак минус перед этим членом означает, что для увеличения 1 при более высокой температуре требуется добавлять меньше катализатора, и наоборот. Парное взаимодействие ХвХа со знаком минус свидетельствует, вероятно, о том, что с увеличением дозировки сокатализатора следует уменьшать давление водорода, и наоборот. Из дальнейшего анализа следует, что давление водорода оказывает положительное влияние на выход глицерина повышение температуры немного уменьшает выход глицерина, а повышение избытка Са(ОН)г увеличивает его, но в незначительной степени (из-за ма- [c.134]
Квантово-механическая модель атома водорода (результаты решения уравнения Шрёдингера). Квантовые числа атома водорода
Квантовая механика без привлечения постулатов Бора позволяет получать решение задачи об энергетических уровнях как для атома водорода и водородоподобной системы, так и для более сложных атомов. Будем рассматривать водородоподобный атом, содержащий единственный внешний электрон. Электрическое поле, создаваемое ядром, является примером центрального поля. Поскольку масса ядра водородоподобного атома во много раз больше массы электрона (различие для атома водорода составляет почти 2000 раз), то приближенно можно считать, что она бесконечно велика и что ядро все время находится в начале координат (ядро неподвижно). Тогда задачу о водородоподобном атоме можно представить как задачу о движении электрона в фиксированном поле сил с потенциалом
где Z — атомное число; е — абсолютное значение заряда электрона; г — радиальная переменная — расстояние между электроном и ядром. Потенциал U(г) описывает кулоновское поле ядра. Движение электрона в таком поле можно рассматривать как движение в некоторой сферической потенциальной «яме» (рис. 28.5, а).
Рис. 28.5. Квантово-механическая модель атома водорода: а — схема энергетических уровней водородоподобного атома; б — положение точки в сферической
Учитывая, что U — —k-, стационарное уравнение Шрёдингера (26.15) имеет вид
где волновая функция ф(дс, у, z) описывает состояние электрона в атоме; Е — значения полной энергии электрона в атоме, которые требуется найти при условии, что ф удовлетворяет требованиям конечности, однозначности и непрерывности (см. стандартные условия в подтеме 26.6). Отметим, что в этой задаче удобно использовать сферическую систему координат (г, 9, ф), центр которой совпадает с центром ядра атома (рис. 28.5, б). Поэтому применим соотношения, связывающие сферические и декартовы координаты:
х = г sin 9 cos ф, у — г sin 0 sin ф, z —г cos0.
Уравнение Шрёдингера (28.11) в сферических координатах имеет вид
где волновая функция теперь является функцией сферических координат ф = ф(/ 0, ф).
Можно показать, что уравнение (28.11а) имеет однозначные, конечные и непрерывные решения при любых положительных значениях энергии, а также при дискретных отрицательных значениях энергии:
Формула (28.12) определяет возможные значения энергии водородоподобного атома. Случай Е > 0 соответствует электрону, оторванному от атома (свободный электрон). Случай Е 2 тее 4 /(2Н 3 ). В отличие от энергии Еп терм — величина положительная, и чем ниже уровень, тем больше его значение.
Собственные волновые функции уравнения (28.11а) Ф = >п1т (г, 0, ф) определяются квантовыми числами: главным л, орбитальным / и магнитным Ш/.
Квантовые числа атома водорода. Стационарные состояния атома водорода без учета спина можно охарактеризовать набором трех квантовых чисел. Квантовое число п из теории Бора сохраняется и в квантовой механике и называется главным квантовым числом. Оно определяет энергетические уровни атома водорода:
Для атома водорода в состоянии с заданным главным квантовым числом п орбитальное квантовое число / принимает следующие значения:
Число / определяет модуль орбитального механического момента атома, т.е. момента импульса электрона относительно ядра:
Магнитное квантовое число т, при данном / принимает следующие значения:
Число т, и определяет проекцию орбитального механического момента на произвольно выбранное направление Z:
Таким образом, основное состояние атома водорода, соответствующее л = 1, характеризуется следующими квантовыми числами: / = 0 и т, = 0.
Уравнение Шредингера для атома водорода: переход к сферическим координатам и разделение переменных
Поместим начало координат в то положение, в котором находится положительно заряженный протон ядра атома водорода, который будем считать неподвижным точечным зарядом (адиабатическое приближение). Соответственно сказанному выше уравнение Шредингера для такого атома имеет вид (8.12)
где и — приведенная масса (см. формулу (1.87)) электрона и ядра [1] (близкая к массе электрона); Щх, у, z) — его потенциальная энергия в кулоновском поле протона, равная (см. подраздел 5.14, формула (5.30))
где г = yjx [2] + у [2] +z [2] ; е — заряд электрона; so — электрическая постоянная.
Теперь выражение (8.38) для потенциальной энергии надо подставить в уравнение Шредингера и решить его.
Как указывалось, это одна из немногочисленных задач квантовой механики, точно решаемых в аналитической форме, — ее решение требует знания специальных функций. Последовательное решение не является нашей целью: мы пойдем по пути наглядных упрощений, стараясь не терять при этом стройности и строгости изложения.
Так как потенциальная энергия зависит только от расстояния между электроном и протоном, первое, что нужно сделать на пути решения поставленной задачи, это перейти от декартовых (х, у, z) к сферическим (г, 0, ф) координатам [2] .
Связь между декартовыми и сферическими координатами произвольной точки А в пространстве, положение которой характеризуется радиус-вектором г (рис. 8.16), такова
Рис. 8.16. Связь декартовых и сферических координат
При этом элемент объема dV= dxdydj при переходе к сферическим координатам преобразуется в dV = /^(sin 0)drdcpd0. Обратим внимание на то, что часто при решении квантово-механических задач одна из трех координатных осей, чаще всего OZ, формально выделяется из всех. Говорят, что эта ось является выделенной. Во всех случаях, когда атом находится под влиянием внешних воздействий, ось Oz направляется вдоль характеристики воздействия — векторов напряженности электрического или магнитного полей и др.
В этом случае оператор Лапласа в уравнении Шредингера (8.12) тоже надо представить в сферических координатах:
В результате уравнение для атома водорода в этих координатах примет вид:
Представим функцию ?(г, 0,9) в виде произведения трех независимых друг от друга функций, где каждая функция-сомножитель зависит только от одного аргумента: либо от длины г радиус-вектора г, либо от одного из углов 0 или 9:
так называемая угловая часть волновой функции. Такое разбиение, вообще говоря, не является самоочевидным, но оно справедливо для данной задачи. Удобство такого представления ? (г, 0, ф) заключается в том, что подстановка волновой функции в форме (8.42) в уравнение (8.41) разбивает его на три независимых друг от друга уравнения. Как можно, например, разделить уравнение на зависимые только от углов 0 и от ф части, будет показано далее. Функция R(r) называется радиальной частью волновой функции.
Рассмотрим сначала движение электрона по поверхности сферы при фиксированном значении радиус-вектора г. Этому соответствует
г = const и ф) _ q _ так как у(05 ф) ф /(/•). В результате можно
будет найти распределение электронов на сфере выбранного радиуса. В уравнении (8.41) первый член становится равным нулю, и уравнение для угловой части волновой функции принимает вид
Теперь задача сводится к анализу движения частицы по поверхности сферы на фиксированном расстоянии от начала координат и носит название задачи о жестком ротаторе. Классический жесткий ротатор представлен в подразделе 1.2.9 (см. рис. 1.17). Напомним, что вектор момента импульса L орбитального движения электрона (в рамках воровской модели атома он квантуется) определяется по формуле
Он направлен перпендикулярно векторам г и р = ти. Если угол между векторами г и р составляет 90°, то величина момента импульса
В подразделе 1.2.9 было показано, что вращение двух масс т и т2, находящихся на расстоянии d друг от друга, вокруг неподвижного цен-
тра масс может быть заменено вращением одной массы р = —
(которую называют приведенной массой) вокруг оси, отстоящей от р на то же расстояние d. Результат проведенного анализа одинаково применим и к вращению двухатомной молекулы относительно ее центра масс, и к «вращению» [6] электрона относительно ядра. Интересно еще раз отметить, что приведенная масса атома водорода близка к массе электрона, а не к массе протона, как это может показаться. Момент инерции жесткого ротатора
Здесь уместно будет сделать одно важное замечание. Ведь только в полуклассической модели атома Бора электрон представляется обращающимся вокруг ядра. В этом случае его движение характеризуется такими классическими свойствами, как момент импульса, кинетическая энергия вращения и др. Как мы уже знаем, характеризовать движение электрона как вращение по орбите (т.е. движение по определенной траектории) в квантовой механике в силу принципа неопределенности нельзя, это было показано в подразделе 8.2. Вместе с тем почти все классические характеристики вращательного движения сохраняются и в квантовой механике. Однако дать им здесь такое же наглядное представление, как в классической физике, не представляется возможным.
Уравнение Шредингера
Вы будете перенаправлены на Автор24
Предпосылки вывода уравнения Шредингера
Основная идея волновой механики заключается в том, что для таких малых тел, как электрон, нельзя с определенностью сказать, где оно находится в данное время и куда направляется. Можно установить только относительную вероятность его нахождения в том или ином месте и наличие определенного количества движения в определенный момент времени.
В соответствии с волновой механикой какая-либо система – атом, молекула, электрон и т.д. – описывается функцией состояния или волновой функцией, обозначаемой $psi$ («пси»), которая является функцией координат всех частиц, образующих эту систему. Следовательно, величина $psi$ зависит только от положения всех частиц в пространстве.
В 1924 г. де Бройль предположил, что точно также, как свет, который, как обычно считают, имеет волновую природу, на самом деле при определенных обстоятельствах ведет себя, как будто он состоит из частиц – квантов, — так и очень малые частицы, такие, как электроны, также могут обладать волновыми свойствами. Де Бройль предположил, что с пучком электронов следует связывать длину волны, определяемую уравнением
где $hbar$ – постоянная Планка ($6,626cdot 1034 Джcdot с$ или $6,626cdot 10-27 эргcdot с$), а $p$ – количество движения (импульс) электрона в пучке, т.е. его масса, умноженная на его скорость.
Физическое подтверждение волновой природы электрона было продемонстрировано в 1927 – 1928 гг. Дейвиссоном, Джермером и Томсоном, которые показали, что пучок электронов может испытывать дифракцию на подходящей решетке (атомы в кристалле золота), аналогичную дифракции пучка света.
Рисунок 1. Дифракция пучка электронов
На преграду с двумя узкими щелями направлен параллельный пучок моноэнергетических (т.е. обладающих одинаковой кинетической энергией) электронов (рис. 1. а). За преградой находится фотопластина $Фn$. При закрытии щели номер $2$ и экспонировании в течение времени $t$ почернение на проявленной фотопластине будет характеризоваться кривой $1$ (рис. 1. б). При закрытии щели номер $1$, соответственно, почернение на фотопластине будет соответствовать кривой $2$. Однако в случае, когда открыты обе щели картина почернения фотопластины (рис. 1. в) отнюдь не эквивалентна наложению двух первых картин. Зато она аналогична картине, получающейся при интерференции двух когерентных световых волн.
Готовые работы на аналогичную тему
Тот факт, что системы малых частиц проявляют, по крайней мере, при определенных условиях, волновые свойства, предполагает возможность описания таких систем уравнениями, подобными те, которые описывают другие виды волнового движения, например, волны, которые распространяются вдоль колеблющейся струны, или волновое движение, приписываемое электромагнитному излучению. Действительно, можно начать с волнового уравнения, соответствующего электромагнитным волнам, и путем определенных замен, превратить его в уравнение, соответствующее нашему случаю. Хотя эти замены диктуются физическими причинами, они в основном произвольны и могут быть приняты только потому, что приводят к уравнению, которое, как показывает опыт, позволяет получить правильное решение физических задач. Поэтому следует принять волновое уравнение как постулат, так как у химиков основной интерес вызывает применение волнового уравнения к атомным и молекулярным системам, а не физические и математические соображения, которыми руководствовался Шредингер, впервые его предложивший в 1925 г.
Общий вид уравнения Шредингера
Рисунок 2. Эрвин Шрёдингер (1887 — 1961)
Волновое уравнение, применяемое для расчета стационарных состояний системы, можно записать в символическом виде:
где $H$ представляет собой определенный способ выражения общей энергии системы, а $E$ – числовое значение этой энергии. Для всех систем, которые обычно интересуют химиков, общая энергия представляет собой сумму кинетической энергии $Т$ и потенциальной энергии $V$:
Это соотношение было широко использовано физиком-теоретиком Гамильтоном, поэтому $H$ часто называют функцией Гамильтона, а $mathcal H$ гамильтонианом системы.
Уравнение Шредингера на примере атома водорода
Рассмотрим модель атома водорода, предложенную Бором. Для простоты предположим, что тяжелое ядро закреплено (оно почти, но не совершенно неподвижно, когда электрон движется вокруг него). Тогда полная кинетическая энергия $Т$ системы представляет собой просто кинетическую энергию электрона
где $m$ – масса электрона и $nu$ – его скорость. Потенциальная энергия системы есть просто энергия, возникающая вследствие электростатического взаимодействия (гравитационные силы приблизительно в $10^<18>$ раз меньше), и ее можно выразить как
где $e$ — заряд электрона, $r$ — радиус орбиты, знак минус появляется вследствие того, что заряд одной из частиц положителен $(+)$, а другой отрицателен $(-)$. Поэтому для атома водорода функция Гамильтона в классической (т.е. доквантовомеханической) физике равна:
Если использовать понятие количества движения электрона $p=mnu$, данное уравнение запишется в следующем виде:
Теперь для перехода от классического описания этой или какой-либо другой системы к описанию при помощи волновой механики, необходимо взять функцию Гамильтона (уравнение 6) и произвести в ней определенные замены: в функции Гамильтона количество движения следует заменить выражением
Таким образом, гамильтониан для атома водорода в его квантовомеханической форме $<mathcal H>$ следует записать в виде
Если теперь это выражение гамильтониана подставить в общее волновое уравнение (уравнение 1), то получим:
Это и есть волновое уравнение для атома водорода. Из уравнения 9 следует, что нужно вторые производные функции $psi $ сложить и умножить на $-<<hbar >^2>/<8<pi >^2m>$, затем к этому добавить $left(-/right)psi $, тогда получим величину, тождественную Е$psi $. Если найдена функция $psi $, то говорят, что она является решением волнового уравнения, и ее называют волновой функцией. Вообще, может быть несколько различных функций $psi_1$, $psi_2$, . , $psi_n$, которые являются решениями уравнения 9, причем каждой соответствует свое значение энергии $Е_1$, $Е_2$, . , $Е_n$.
http://bstudy.net/704976/estestvoznanie/uravnenie_shredingera_atoma_vodoroda_perehod_sfericheskim_koordinatam_razdelenie_peremennyh
http://spravochnick.ru/himiya/atomnye_i_molekulyarnye_orbitali/uravnenie_shredingera/

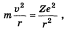









/Lyakishev.files/image002.png)



















 — постоянная тонкой структуры,
— постоянная тонкой структуры, — собственное значение оператора полного момента импульса.
— собственное значение оператора полного момента импульса. (в системе СИ),
(в системе СИ),
 — Боровский радиус.
— Боровский радиус. — обобщённые полиномы Лагерра степени
— обобщённые полиномы Лагерра степени  от функции
от функции 
 — нормированные на единицу сферические функции.
— нормированные на единицу сферические функции.
















