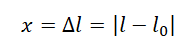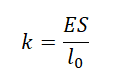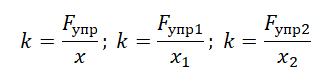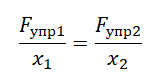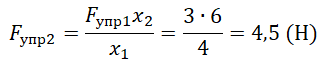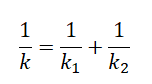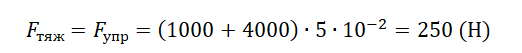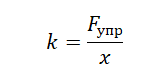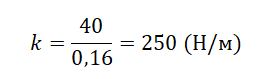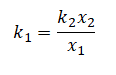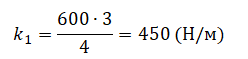Сила упругости — сила, которая возникает при деформациях тел в качестве ответной реакции на внешнее воздействие. Сила упругости имеет электромагнитную природу.
Деформация — изменение формы или объема тела.
Виды деформаций
- сжатие;
- растяжение;
- изгиб (сжатие и растяжение в комбинации);
- сдвиг;
- кручение (частный случай сдвига).
Сила упругости обозначается как Fупр. Единица измерения — Ньютон (Н). Сила упругости направлена противоположно перемещению частиц при деформации.
Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.
Примеры упругой деформации:
- Сжатый воздушный шарик распрямляется после того, как его отпустят.
- Если согнуть ластик, а затем отпустить, он распрямится.
- Мостик из доски, перекинутой через ручей, прогибается под пешеходом. Но когда пешеход ступает на землю, доска распрямляется.
Примеры пластической деформации:
- Скомканная бумага остается скомканной и после того, как ее отпустили.
- Пластилин сохраняет форму вылепленной из него фигуры.
- Согнутая металлическая пластина остается согнутой.
Закон Гука
При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.
Закон Гука
Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.
x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.
Абсолютное удлинение определяется формулой:
l0 — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.
Коэффициент жесткости тела определяется формулой:
E — модуль упругости (модуль Юнга). Каждое вещество обладает своим модулем упругости. S — площадь сечения тела.
Важно! Закон Гука не работает в случае, если деформация была пластической.
Пример №1. Под действием силы 3Н пружина удлинилась на 4 см. Найти модуль силы, под действием которой удлинение пружины составит 6 см.
Согласно третьему закону Ньютона модуль силы упругости будет равен модулю приложенной к пружине силе. В обоих случаях постоянной величиной окажется только жесткость пружины. Выразим ее из закона Гука и применим к каждому из случаев:
Приравняем правые части формул:
Выразим и вычислим силу упругости, возникающую, когда удлинение пружины составит 6 см:
Полезные факты
Если пружину растягивают две противоположные силы, то модули силы упругости и модули этих сил равны между собой:
F1 = F2 = Fупр
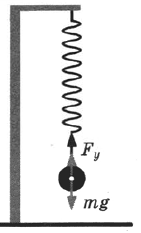
Если груз подвешен к пружине, сила упругости будет равна силе тяжести, действующей на это тело:
Fупр = Fтяж = mg.
Если пружины соединены параллельно, их суммарный коэффициент жесткости будет равен сумме коэффициентов жесткости каждой из этих пружин:
Если пружины соединены последовательно, их обратное значение суммарного коэффициента жесткости будет равен сумме обратных коэффициентов жесткости для каждой из пружин:
Пример №2. Две пружины соединены параллельно. Жесткость одной из пружин равна 1000 Нм, второй — 4000 Нм. Когда к пружинам подвесили груз, они удлинились на 5 см. Найти силу тяжести груза.
Переведем сантиметры в метры: 5 см = 5∙10–2 м.
Запишем закон Гука с учетом параллельного соединения пружин:
Модуль силы тяжести согласно третьему закону Ньютона равен модулю силы упругости. Отсюда:
Задание E17590
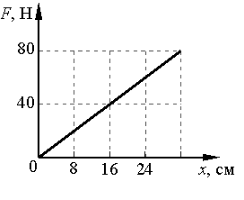
а) 250 Н/м
б) 160 Н/м
в) 2,5 Н/м
г) 1,6 Н/м
Алгоритм решения
2.Выразить из закона Гука формулу для вычисления коэффициента упругости.
3.Выбрать любую точку графика и извлечь из нее исходные данные.
4.Перевести единицы измерения в СИ.
5.Вычислить коэффициент упругости, используя извлеченные из графика данные.
Решение
Запишем закон Гука:
Fупр = kx
Отсюда коэффициент упругости пружины равен:
Возьмем на графике точку, соответствующую удлинению пружины 16 см. Ей соответствует модуль силы упругости, равный 40 Н. Переведем сантиметры в метры: 16 см = 0,16 м.
Вычислим жесткость пружины:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18489
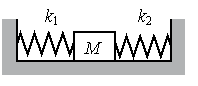
Алгоритм решения
- Записать исходные данные.
- Записать закон Гука.
- Применить закон Гука к обеим пружинам.
- Применить третий закон Ньютона.
- Выразить жесткость первой пружины.
- Вычислить искомую величину.
Решение
Запишем исходные данные:
- Сжатие первой пружины x1 — 4 см.
- Сжатие второй пружины x2 — 3 см.
- Жесткость второй пружины k2 — 600 Н/м.
Запишем закон Гука:
Fупр = kx
Применим этот закон к обеим пружинам:
Fупр1 = k1x1
Fупр2 = k2x2
Силы упругости обеих пружин уравновешены, так как тело между ними покоится. Согласно третьему закону Ньютона:
Fупр1 = Fупр2
Отсюда:
k1x1 = k2x2
Выразим отсюда жесткость первой пружины:
Подставим известные данные и вычислим:
Внимание! В данном случае переводить единицы измерения в СИ не нужно. Отношение длин постоянно независимо от выбранной единицы измерения.
Ответ: 450
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17520
Две упругие пружины растягиваются силами одной и той же величины F. Удлинение второй пружины Δl2 в 2 раза меньше, чем удлинение первой пружины Δl1. Жёсткость первой пружины равна k1, а жёсткость второй k2 равна…
а) 0,25k1
б) 2k1
в) 0,5k1
г) 4k1
Алгоритм решения
- Записать исходные данные.
- Записать закон Гука.
- Применить закон Гука к обеим пружинам.
- Выразить величину жесткости второй пружины.
Решение
Записываем исходные данные:
- Первая и вторая пружины растягиваются под действием одной и той же силы. Поэтому: F1 = F2 = F.
- Удлинение первой пружины равно: Δl1 = 2l.
- Удлинение второй пружины вдвое меньше удлинения первой. Поэтому: Δl2 = l.
Закон Гука выглядит следующим образом:
F = k Δl
Применим закон Гука для обеих пружин:
F1 = k1 Δl1
F2 = k2 Δl2
Так как первая и вторая силы равны, можем приравнять правые части выражений. Получим:
k1 Δl1 = k2 Δl2
Перепишем выражение с учетом значения удлинений первой и второй пружин:
k1 2l = k2 l
«l» в левой и правой частях выражения взаимоуничтожаются, отсюда жесткость второй пружины равна:
k2 = 2k1
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.9k
Содержание:
- Определение и формула силы упругости
- Характеристики упругих свойств твердых тел
- Продольное растяжение (сжатие)
- Деформация сдвига
- Единицы измерения силы упругости
- Примеры решения задач
При действии на тело внешней силы онодеформируется (происходит изменение размеров, объема и часто формы тела). В ходе деформации
твердого тела возникают смещения частиц, находящихся в узлах кристаллической решетки из начальных положений равновесия в новые положения.
Такому сдвигу препятствуют силы, с которыми частицы взаимодействуют. В результате появляются внутренние силы упругости, уравновешивающие
внешние силы. Эти силы приложены к деформированному телу. Величина сил упругости пропорциональна деформации тела.
Определение и формула силы упругости
Определение
Силой упругости называют силу, имеющую электромагнитную природу, которая возникает в результате деформации тела, как ответ на внешнее воздействие.
Упругой называют деформацию, при которой после прекращения действия внешней силы тело восстанавливает свои прежние форму и размеры,
деформация исчезает. Деформация носит упругий характер только в том случае, если внешняя сила не превышает некоторого определенного значения,
называемого пределом упругости. Сила упругости при упругих деформациях является потенциальной. Направление вектора силы упругости противоположно
направлению вектора перемещения при деформации. Или по-другому можно сказать, что сила упругости направлена против перемещения частиц при деформации.
Характеристики упругих свойств твердых тел
Упругие свойства твердых тел характеризуют при помощи напряжения, которое часто обозначают буквой
$sigma$ .
Напряжение – это физическая величина, равная упругой силе, которая приходится на единичное сечение тела:
$$sigma=frac{d F_{u p r}}{d S}(1)$$
где dFupr – элемент силы упругости тела; dS – элемент площади сечения тела. Напряжение называется нормальным,
если вектор $d bar{F}_{u p r}$ перпендикулярен к dS.
Формулой для расчета силы упругости служит выражение:
$$d F_{u p r}=sigma d S=K frac{Delta x}{x} d S(2)$$
где $frac{Delta x}{x}$ — относительная деформация,
$Delta x$ – абсолютная деформация, x–первоначальное значение величины, которая характеризовала
форму или размеры тела; K – модуль упругости (
$k = sigma$ при
( $frac{Delta x}{x} = 1$ ). Величину обратную модулю упругости называют коэффициентом упругости.
Проще говоря, сила упругости по величине пропорциональная величине деформации.
Продольное растяжение (сжатие)
Продольное (одностороннее) растяжение состоит в том, что под действием растягивающей (сжимающей) силы происходит увеличение
(уменьшение) длины тела. Условием прекращения такого рода деформации является выполнение равенства:
$F = F_{upr} (3)$
где F – внешняя сила, приложенная к телу, Fupr – сила упругости тела. Мерой деформации в рассматриваемом процессе является
относительное удлинение (сжатие) $left(frac{Delta l}{l}right)$ .
Тогда модуль силы упругости можно определить как:
$$F_{u p r}=E frac{Delta l}{l} S(4)$$
где E – модуль Юнга, который в рассматриваемом случае равен модулю упругости (E=K) и характеризующий упругие свойства тела;
l – первоначальная длина тела; $Delta l$ – изменение длины при нагрузке
F=F_upr. При $Delta l=l E=frac{F}{S}=sigma$ – площадь поперечного сечения образца.
Выражение (4) называют законом Гука.
В простейшем случае рассматривают силу упругости, которая возникает при растяжении (сжатии) пружины. Тогда закон Гука записывают как:
$$F_{x}=k x(5)$$
где Fx – модуль проекции силы упругости; k – коэффициент жесткости пружины, x – удлинение пружины.
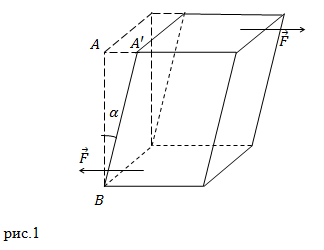
Деформация сдвига
Сдвигом называют деформацию, при которой все слои тела, являющиеся параллельными некоторой плоскости, смещаются друг относительно друга.
При сдвиге объем тела, которое было деформировано, не изменяется. Отрезок, на который смещается одна плоскость относительно другой,
называют абсолютным сдвигом (рис.1 отрезок AA’). Если угол сдвига ($alpha$) мал, то
$alpha approx t g alpha=frac{A A^{prime}}{A B}$ . Этим углом ? (относительный сдвиг)
характеризуют относительную деформацию. При этом напряжение $sigma$ равно:
$$sigma=G alpha(6)$$
где G – модуль сдвига.
Единицы измерения силы упругости
Основной единицей измерения сил упругости (как и любой другой силы) в системе СИ является: [Fupr]=H
В СГС: [Fupr]=дин
Примеры решения задач
Пример
Задание. Какова работа силы упругости при деформации пружины жёсткость, которой равна k? Если первоначальное удлинение
пружины составляло x1, последующее удлинение составило x2.
Решение. В соответствии с законом Гука модуль силы упругости найдем как:
$$F = kx (1.1)$$
При этом сила упругости при первой деформации будет равна:
$$F_1 = kx_1 (1.2)$$
В случае второй деформации имеем:
$$F_2 = kx_2 (1.3)$$
Работу (A) сил упругости можно найти как:
$$A=langle Frangle S cos alpha(1.4)$$
где $langle Frangle$ — средняя величина силы упругости, равная:
$$langle Frangle=frac{F_{1}+F_{2}}{2}(1.5)$$
S- модуль перемещения, равный:
$S = x_2 — x_1 (1.6)$
$alpha=180^{circ}$ — угол между векторами перемещения и вектором сил упругости (эти векторы направлены в противоположные стороны).
Подставим выражения (1.2), (1.3), (1.5) и (1.6) в формулу для работы (1.4), получим:
$$A=frac{k x_{1}+k x_{2}}{2}left(x_{2}-x_{1}right) cos left(180^{circ}right)=-frac{k x_{1}+k x_{2}}{2}left(x_{2}-x_{1}right)$$
Ответ. $A=-frac{k}{2}left(x_{1}+x_{2}right)left(x_{2}-x_{1}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
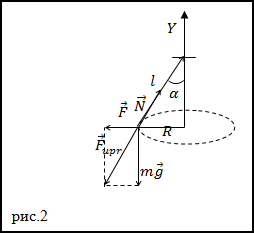
Задание. Тело массой m (которое можно считать материальной точкой) привязано к резиновому шнуру.
Это тело описывает в горизонтальной плоскости окружность с частотой вращения n. Угол отклонения шнура от вертикали равен
$alpha$.
Жёсткость шнура равна k. Какова длина нерастянутого шнура (l0)?
Решение. Сделаем рисунок.
Сила натяжения (N) шнура вызывает его растяжениена величину ($Delta l$). При этом возникающая
сила упругости равна по модулю и противоположна по направлению силе натяжения:
$$bar{F}_{u p r}=-bar{N}(2.1)$$
Сила натяжения шнура равна (из рис.2 и второго закона Ньютона):
$$N=frac{m g}{cos alpha}(2.2)$$
Но так как сила натяжения равна по модулю силе упругости, то можно записать, что:
$$N=k Delta l rightarrow Delta l=frac{N}{k}(2.3)$$
Рассмотрение рис.2 дает:
$$frac{l}{R}=frac{N}{F} rightarrow l=frac{N R}{F}(2.4)$$
где l – длина растянутой нити, R – радиус окружности по которой движется точка. Применяя второй закон Ньютона, получим:
$$F=N sin alpha=m frac{v^{2}}{R}=4 pi^{2} n^{2} m R(2.5)$$
Подставим в (2.4) выражение для F, получаем:
$$l=frac{N}{4 pi^{2} n^{2} m}(2.6)$$
В таком случае длина нерастянутого шнура:
$$l_{0}=l-Delta l=frac{N}{4 pi^{2} n^{2} m}-frac{N}{k}=left(frac{1}{4 pi^{2} n^{2} m}-frac{1}{k}right) frac{m g}{cos alpha}$$
Ответ. $l_{0}=left(frac{1}{4 pi^{2} n^{2} m}-frac{1}{k}right) frac{m g}{cos alpha}$
Читать дальше: Формула скорости.
Силы упругости
— силы, возникающие при упругой
(обратимой) деформации тел.
Закон Гука: сила
упругости тела прямо пропорциональна
упругой деформации тела.
Закон Гука для винтовой пружины
На рис.11.1 показана
винтовая пружина, закрепленная одним
концом на опоре в т.А. К незакрепленному
концу пружины приложена (рис.11.1а) внешняя
сила Fвнеш,
направленная по оси пружины от опоры.
Пружина находится в растянутом состоянии
(может быть в сжатом состоянии, если
Fвнеш
будет направлена к опоре).
Внешняя сила
Fвнеш
равна по модулю силе упругости пружины
и направлена в противоположную сторону:
(11.1)
Сила
упругости пружины приложена к внешнему
телу, вызывающему растяжение (или сжатие)
пружины.
Сила упругости пружины
(11.2)
где к — жесткость
винтовой пружины; r0
= (r
r0)
— перемещение незакреплённого конца
пружины (рис.11.1,в), находящейся в растянутом
(может быть в сжатом) состоянии под
действием внешней силы; r0,
r
— радиус-векторы незакреплённого конца
пружины, находящейся в ненагруженном
(рис.11.1,а) и нагруженном (рис.11.1,б) состоянии
соответственно. Начало координат (см.
рис.11.1б) находится в закрепленном на
опоре конце пружины — точке А (в общем
случае начало координат может находится
в любой точке).
Единица жесткости
пружины
— ньютон на метр: [к] = Н/м.
Удлинение пружины
при растяжении (укорочение
при сжатии)
(11.3)
где L0
— длина ненагруженной пружины (см.
рис.11.1,а), L — длина нагруженной пружины
(см. рис.11.1,б,в).
Модуль силы
упругости пружины
прямо пропорционален модулю удлинения
при растяжении (модулю укорочения при
сжатии) пружины:
(11.4)
Если начало
координат находится в точке, где находился
незакрепленный конец ненагруженной
пружины, то
Fупр
=
кr. (11.5)
В этом случае
проекция силы упругости на ось Ох
(11.6)
где х — координата
(называемая также смещением)
конца пружины,
к которому приложена внешняя сила.
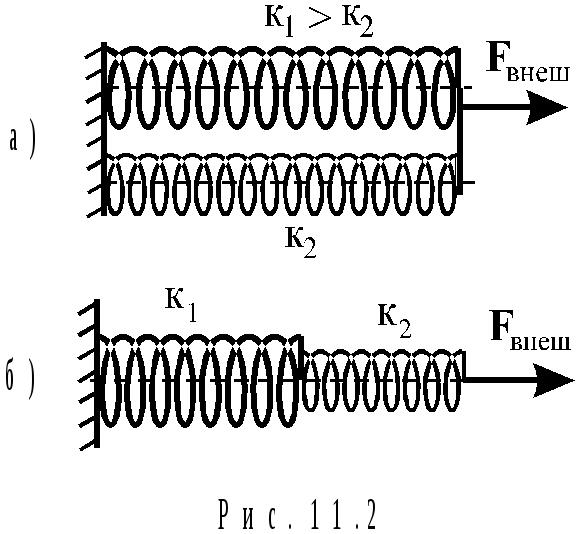
Жесткость системы
соединенных пружин
При параллельном
соединении пружин (рис.11.2,а) жесткости
пружин складываются:
(11.7)
при последовательном
соединении пружин (рис.11.2б) складываются
величины, обратные жесткостям пружин:
(11.8)
где кi
— жесткость i–й пружины, n —
число пружин.
§12. Силы тяготения
Закон всемирного
тяготения
Между двумя
материальными точками действуют силы
тяготения (гравитационные силы),
являющиеся силами взаимного притяжения,
модули которых прямо пропорциональны
произведению их масс и обратно
пропорциональны квадрату расстояния
между ними. Силы направлены по линии,
проходящей через эти материальные
точки.
М
точки (при
использовании в законе всемирного
тяготения) — тела, максимальные линейные
размеры которых много меньше расстояния
между ними: Li max
<< r (i =
1,2).
На рис. 12.1 показана
материальная точка (м.т.) массой m1,
находящаяся в начале координат, и м.т.
массой m2,
которая
находится в точке, радиус-вектор которой
r.
Сила тяготения
Fтяг,
действующая со стороны первой материальной
точки на вторую:
(12.1)
где G
гравитационная постоянная, равная
6,6710-11
Нм2/кг2,
r расстояние
между м.т. (модуль радиус-вектора r).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
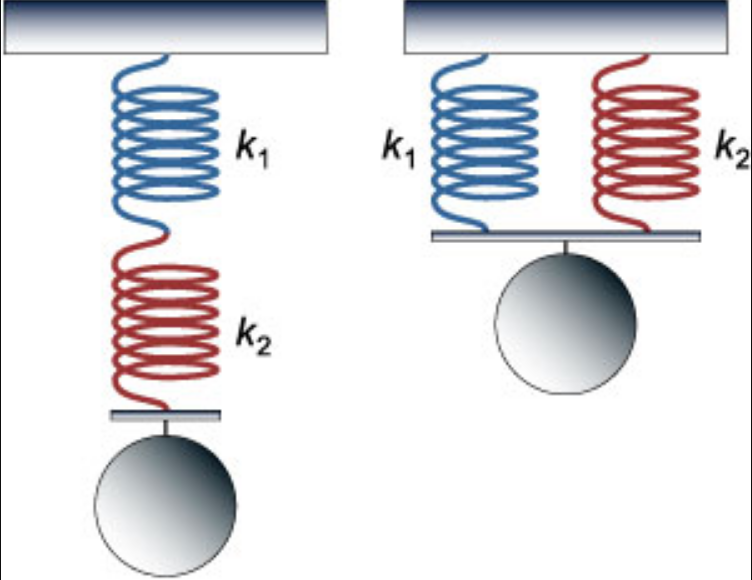
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
На все тела, которые находятся на Земле, действует сила тяжести. Все они стремятся под ее действием упасть вниз. Но не похоже, чтобы все в мире лежало на земле.
На еду в вашей тарелке действует сила тяжести, но она же не проваливается сквозь тарелку. На учебник на вашей парте тоже действует сила тяжести. Но стол от этого не придавливается к полу.
Значит, существует некая сила, уравновешивающая силу тяжести. На данном уроке мы узнаем, что же это за сила.
Определение силы упругости
Начнем с рассмотрения простого опыта (рисунок 1).
На два бруска положим доску. На доску поставим гирю. Мы увидим, что доска прогнется. Что же здесь происходит со стороны физики?
На гирю действует сила тяжести, она начинает двигаться вниз и прогибает доску. Доска деформируется из-за взаимодействия с гирей. Значит, возникает еще одна сила, с которой доска в ответ действует на гирю.
Сила тяжести, действующая на гирю, направлена вертикально вниз, а другая сила направлена вертикально вверх. Поэтому она и уравновесила силу тяжести. Нашу искомую силу называют силой упругости.
Сила упругости — это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
Сила упругости — векторная величина:
- обозначается как $vec{F}_{упр}$
- ее модуль обозначается как $F_{упр}$
В ситуации на рисунке 1, опора (доска) прогибается. Чем сильнее этот прогиб, тем больше сила упругости. Когда сила упругости и сила тяжести становятся равны, то опора и тело останавливаются. Так они приходят в равновесие.
Деформация и ее виды
Рассмотрим следующий случай (рисунок 2). Подвесим тело на нити.
В таких конструкциях нить часто называют подвесом. Когда мы подвесили тело, нить начала растягиваться — в ней возникла сила упругости.
Чем больше нить растягивается, тем больше становится сила упругости. Как и в случае с опорой, как только сила упругости станет равной силе тяжести, растяжение прекратится.
Когда возникает сила упругости?
Получается, что сила упругости возникает при деформации тел. Если исчезает деформация, то исчезает и сила упругости.
Что называют деформацией тела?
Деформация тела — это любое изменение его формы и размеров.
Какие виды деформаций вы знаете?
Иногда после таких взаимодействий тело, испытывающее деформацию, меняет свои форму и размеры — происходит неупругая (пластическая) деформация. А иногда возвращается в исходное состояние. Тогда деформация называется упругой (рисунок 3).
Дадим определения
Упругая деформация — это деформация, при которой после прекращения воздействия деформирующей силы тело полностью восстановило свою форму и объем.
Пластическая деформация — это деформация, сохраняющаяся после прекращения действия деформирующей силы.
Упругая деформация бывает различных видов:
- Растяжения (рисунок 2)
- Сжатия (рисунок 4)
- Сдвига (при такой деформации нагрузка прикладывается параллельно основанию тела, и одна часть тела сдвигается относительно другой (рисунок 5));
- Изгиба (рисунок 1);
- Кручения (рисунок 6).
Примеры деформации разных видов
1. Играем на гитаре — кратковременно растягиваем струны
2. Садимся в автомобиль — пружины подвески сжимаются
3. Сидим на тонкой доске — доска прогибается
4. Затягиваем шуруп — происходит кручение отвертки (хоть мы и не видим деформацию отвертки)
5. Двигаем расшатанный стул — происходит сдвиг сиденья относительно пола
Закон Гука
От чего же зависит сила упругости? Роберт Гук, современник Ньютона, ответил на этот вопрос (рисунок 8).
Рассмотрим опыт, изображенный на рисунке 9.
У нас есть штатив, к которому мы прикрепим резиновый шнур. Измерим его длину и обозначим как $l_0$.
Далее подвесим к шнуру чашку с гирей. Шнур удлинится. Снова измерим его длину — теперь она имеет значение $l$.
Шнур изменил свою длину после наших действий. Это изменение (удлинение шнура) мы можем найти по формуле:
$Delta l = l- l_0$,
где $Delta l$ — изменение длины. Знак $Delta$ (греческая буква “дельта”) используется как символ для обозначения изменения между значениями какой-либо величина.
Если мы будем менять гири на чашке, то будет меняться длина шнура, то есть его удлинение (деформация) $Delta l$.
Так мы подошли к закону Гука. Как он формулируется?
Изменение длины тела при растяжении или сжатии прямо пропорционально модулю силы упругости:
$F_{упр} = k Delta l$
Здесь $Delta l$ — изменение длины тела, $k$ — коэффициент пропорциональности, который называется жесткостью. Жесткость тела зависит от материала, формы и размеров тела.