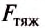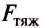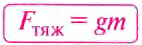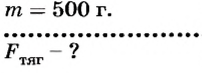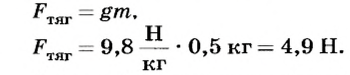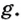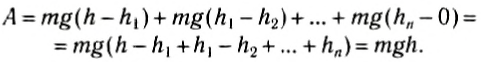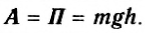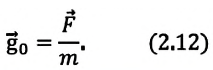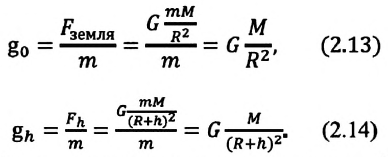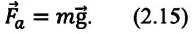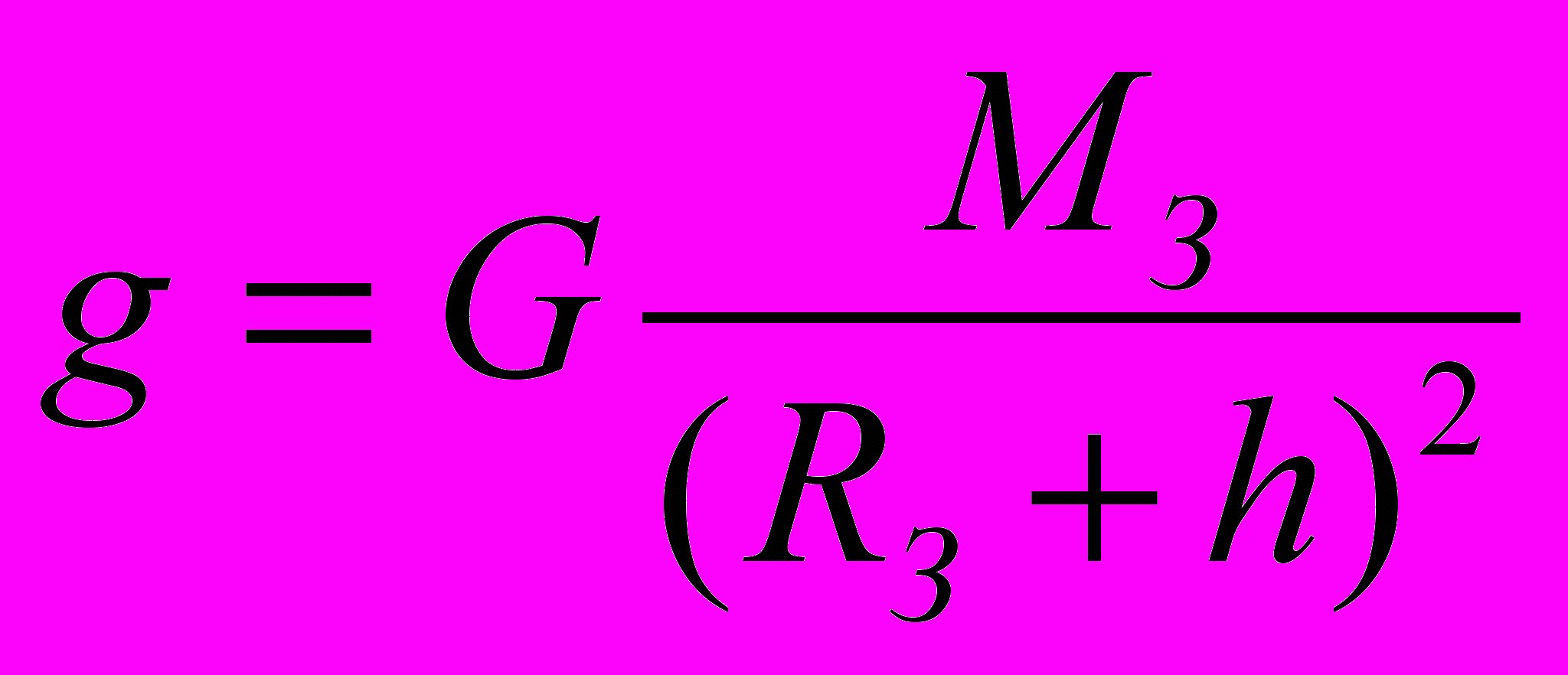Содержание:
- Определение и формула силы тяжести
- Различие между силой тяжести и силой притяжения к Земле
- Единицы измерения силы тяжести
- Примеры решения задач
Определение и формула силы тяжести
Определение
Под воздействием силы притяжения к Земле все тела падают с одинаковыми по отношению к ее поверхности ускорениями.
Такое ускорение называют ускорением свободного падения и обозначают: g. Его величина в системе СИ считается равной
g=9,80665 м/с2 – это так называемое, стандартное значение.
Вышесказанное обозначает то, что в системе отсчета, которая связывается с Землей, на любое тела обладающее массой m действует сила равная:
$$bar{P}=m bar{g}(1)$$
которая называется силой тяжести.
Если тело находится в состоянии покоя на поверхности Земли, тогда сила тяжести уравновешивается реакцией подвеса или опоры, которая удерживает тело от падения (вес тела).
Различие между силой тяжести и силой притяжения к Земле
Если быть точным, то следует заметить, что в результате неинерциальности системы отсчета, которая связывается с Землей,
сила тяжести отличается от силы притяжения к Земле. Ускорение, которое соответствует движению по орбите существенно меньше,
чем ускорение, которое связывается с суточным вращением Земли. Система отсчета, связанная с Землей, осуществляет вращение по
отношению к инерциальным системам с угловой скоростью $omega$=const. Поэтому в случае
рассмотрения перемещения тел по отношению к Земле следует учитывать центробежную силу инерции (Fin), равную:
$$F_{i n}=m omega^{2} r$$
где m – масса тела, r – расстояние от оси Земли. Если тело расположено не высоко от поверхности Земли ( в сравнении с радиусом Земли), то можно считать, что
$$r=R_{Z} cos varphi(3)$$
где RZ – радиус земли, $varphi$ – широта местности.
В таком случае ускорение свободного падения (g) по отношению к Земле будет определено действием сил: силы притяжения к Земле (
$bar{F}_{g}$) и силы инерции (
$bar{F}_{in}$). При этом сила тяжести — есть результирующая этих сил:
$$bar{P}=bar{F}_{g}+bar{F}_{i n}(4)$$
Так как сила тяжести сообщает телу, обладающему массой m ускорение равное
$bar{g}$, то соотношение (1) является справедливым.
Разница между силой тяжести $bar{P}$ и силой притяжения к Земле
$bar{F}_{g}$ небольшая. Так как
$F_{g} gg F_{i n}$.
Как и всякая сила, сила тяжести – векторная величина. Направление силы
$bar{P}$, например, совпадает с направлением нити, натянутой грузом,
которое называют направлением отвеса. Сила
$bar{F}_{g}$ направлена к центру Земли. Значит, нить отвеса направлена
также только на полюсах и экваторе. На других широтах угол отклонения ($alpha$)
от направления к центру Земли составляет величину, равную:
$$alpha approx 0,0018 sin (2 varphi)(5)$$
Разница между Fg-P максимальна на экваторе, она составляет 0,3% от величины силы Fg.
Так как земной шар является сплюснутым около полюсов, то Fg имеет некоторые вариации по широте. Так она у экватора на
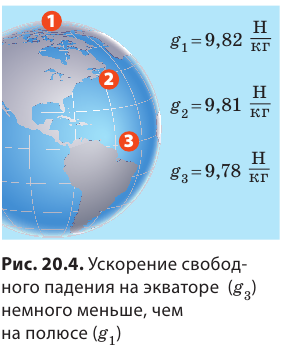
0,2% меньше, чем у полюсов. В результате ускорение g изменяется с широтой от 9,780 м/с2 (экватор) до 9,832 м/с2 (полюса).
По отношению к инерциальной системе отсчета (например, гелиоцентрической СО) тело в свободном падении будет перемещаться с ускорением (a)
отличающимся от g, равным по модулю:
$$a=frac{F_{g}}{m}(6)$$
и совпадающим по направлению с направлением силы $bar{F}_{g}$.
Единицы измерения силы тяжести
Основной единицей измерения силы тяжести в системе СИ является: [P]=H
В СГС: [P]=дин
Примеры решения задач
Пример
Задание. Определите во сколько раз величина силы тяжести на Земле
(P1) больше, чем сила тяжести на Луне (P2).
Решение. Модуль силы тяжести определяется формулой:
$$P=m g(1.1)$$
Если имеется в виду сила тяжести на Земле, то в качестве ускорения свободного падения используем величину
$g_{1} approx 9,8$ м/с^2 . Для вычисления силы тяжести на Луне найдем при помощи справочников ускорение свободного падения на
этой планете, оно равно $g_{1} approx 1,6$ м/с^2 .
$$frac{P_{1}}{P_{2}}=frac{m g_{1}}{m g_{2}}=frac{g_{1}}{g_{2}}$$
Таким образом, для ответа на поставленный вопрос следует найти отношение:
$$frac{P_{1}}{P_{2}}=frac{9,8}{1,6} approx 6,1$$
Проведем вычисления:
Ответ. $frac{P_{1}}{P_{2}} approx 6,1$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
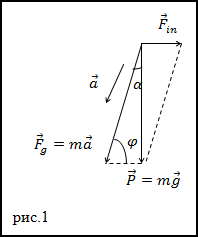
Задание. Получите выражение, которое связывает широту и угол, который образуют вектор силы тяжести и вектор силы притяжения к Земле.
Решение. Угол, который образуется между направлениями силы притяжения к Земле и направлением силы тяжести можно
оценить, если рассмотреть рис.1 и применить теорему синусов. На рис.1 изображены:
$bar{F}_{in}$ – центробежная сила инерции, которая возникает за счет вращения
Земли вокруг оси, $bar{P}$ – сила тяжести,
$bar{F}_{g}$ – сила притяжения тела к Земле. Угол
$varphi$ — широта местности на Земле.
По теореме синусов имеем:
$$frac{sin alpha}{sin varphi}=frac{F_{i n}}{P}(2.1)$$
где выражение для центробежной силы можно определить как:
$$F_{i n}=m omega^{2} R_{Z} cos varphi(2.2)$$
Rz – радиус Земли. При этом:
$$P=m g(2.3)$$
Подставим выражения (2.2) и (2.3) в (2.1), имеем:
$$frac{sin alpha}{sin varphi}=frac{m omega^{2} R_{Z} cos varphi}{m g}=frac{omega^{2} R_{Z} cos varphi}{g}=0,0035 cos varphi$$
где величину $frac{omega^{2} R_{Z}}{g}$ можно рассчитать, если учесть,
что радиус Земли равен Rz=6400 км. Угловая скорость вращения Земли есть:
$$omega=frac{2 pi}{T}=frac{2 pi}{86400}$$
Получаем, что:
$$sin alpha=0,0035 cos varphi sin varphi=0,0018 sin (2 varphi)$$
Ответ. $sin alpha approx 0,0018 sin (2 varphi)$
Читать дальше: Формула ускорения.
Содержание:
Сила тяжести:
Почему все подброшенные вверх тела падают на Землю ? Почему на санках легко съезжать с горки, а вверх их нужно тянуть?
Подбросьте вверх мяч. Поднявшись на некоторую высоту, он начнёт двигаться вниз и упадёт на Землю. Парашютист, выпрыгнувший из самолёта, падает вниз и после раскрытия парашюта. С появлением дождевой тучи на Землю падает густой дождь. Как бы высоко мы не прыгали вверх, всегда опускаемся на Землю.
Все тела, находящиеся на Земле или вблизи неё, взаимодействуют с ней: Земля притягивает тела, а они притягивают Землю.
Поскольку масса у Земли очень большая, то в результате взаимодействия с нею заметно изменяют свои скорости и положения именно тела, а Земля практически остаётся на месте.
Силу, с которой Земля притягивает к себе любое тело, называют силой тяжести.
От чего зависит сила тяжести
Из опыта с яблоками, выполненного ранее, можем сделать вывод, что на два яблока, подвешенных на пружине, действует сила тяжести больше, чем на одно, так как масса двух яблок больше массы одного. Силу тяжести обозначают
Единицей силы тяжести, как и любой другой, в СИ является один ньютон (1Н). Эта единица названа в честь английского учёного Исаака Ньютона, впервые сформулировавшего основные законы движения тел и законы тяготения. 1 ньютон (1 Н) равен силе тяжести, которая действует на тело массой приблизительно 102 г.
Тогда на тело массой 1кг действует сила тяжести 9,81 Н, т. е.
Как, пользуясь единицей силы 1 Н, определить силу тяжести, которая действует на тело любой массы?
Поскольку на тело массой 1 кг действует сила тяжести 9,81 Н, то на тело массой т будет действовать сила тяжести, в т раз большая.
Чтобы определить силу тяжести 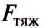
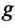
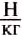
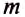
Но притяжение существует не только между Землёй и телами на ней или вблизи неё. Все тела притягиваются друг к другу. Например, притягиваются между собой Земля и Луна, Солнце и Земля или другие планеты, корабли в море, предметы в комнате. Вследствие притяжения Земли к Луне на Земле возникают приливы и отливы (рис. 69).
Вода в океанах поднимается дважды в сутки на несколько метров.
Благодаря силе тяжести атмосфера удерживается возле Земли, реки текут сверху вниз, Луна удерживается возле Земли, планеты двигаются по орбитам вокруг Солнца.
Явление притяжения всех тел Вселенной друг к другу называют всемирным тяготением.
Исаак Ньютон доказал, что сила притяжения между телами тем больше, чем больше массы этих тел и чем меньше расстояние между телами. Если бы сила тяжести на Земле вдруг исчезла, то все незакреплённые на ее поверхности тела от любого небольшого толчка разлетелись бы во все стороны в космическом пространстве.
Каково направление силы тяжести
Опыт. Если взять отвес или привязанный к нити какой-либо предмет (рис. 70), то увидим, что нить с грузиком вследствие действия на него силы тяжести всегда направлена к Земли вдоль прямой, которую называют вертикалью.
Выполнив этот опыт во всех точках Земли, учёные убедились, что сила тяжести всегда направлена к центру Земли.
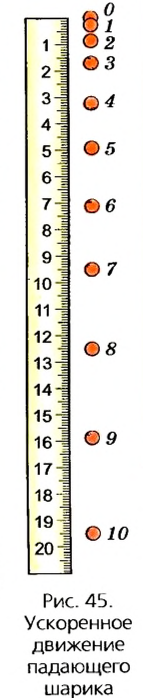
Силу тяжести изображают в виде вертикальной стрелки, направленной вниз и приложенной к определённой точке тела (рис. 71 а, б).
Кстати:
Кроме планет с их спутниками вокруг Солнца двигаются малые планеты, которые еще называют астероидами. Наибольшая из них — Церера — имеет статус карликовой планеты и радиусом почти в 20 раз, а по массе в 7500 раз меньше Земли. Сила тяжести на ней настолько мала, что человек, оттолкнувшись от поверхности планеты, мог бы улететь с нее.
Вот как описывает основатель теории космонавтики К,Э. Циолковский в рассказе «Путь к звездам» условия пребывания человека на этом астероиде: «На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте так же легко могу нести в 30 раз больше. На Земле я могу подпрыгнуть на 50см. На Весте такое же усилие дает прыжок в 30м. Это высота десятиэтажного дома или огромной сосны. Там легко перепрыгивать через рвы и ямы шириной с крупную реку. Можно перепрыгнуть через 15-метровые деревья и дома. И это без разгона».
Сила тяготения
Все тела возле Земли падают на ее поверхность, если их ничто не удерживает. В чем причина этого явления?
Как тела падают на Землю
Рассмотрим фотографию падения шарика, на которой положение шарика фиксировалось на пленке через равные интервалы времени (рис. 45). Если линейкой отмерить расстояние между изображениями шарика в различные моменты времени, то можно заметить, что эти расстояния постепенно увеличиваются. Это свидетельствует о том, что скорость шарика при падении постепенно увеличивается.
Как увеличивается скорость падающего тела
Если вспомнить определение силы, по которому сила изменяет скорость тела, то можно сделать вывод, что на шарик действует сила, направленная к Земле.
Силу, действующую на каждое тело со стороны Земли, называют силой тяготения.
Измерения показывают, что скорость тела, падающего на поверхность Земли при отсутствии сопротивления воздуха, каждую секунду увеличивается на 9,8 
Как рассчитать силу тяготения
Если знать массу тела, то можно рассчитать силу тяготения. Способ таких расчетов подсказывают результаты опытов.
Возьмем динамометр и подвесим к нему гирьку массой 102 г, стрелка динамометра остановится на отметке 1 Н. Если подвесить два таких груза, то динамометр покажет силу 2 Н и т. д. С этого опыта можно сделать вывод, что сила тяжести пропорциональна массе тела.
Сила тяготения пропорциональна массе тела:
Коэффициент пропорциональности 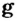
Для расчетов при решении задач иногда принимают, что
Если знать такую зависимость силы тяготения от массы, то можно заранее рассчитать ее значение.
Например, необходимо определить, что покажет динамометр, если на его крючок повесить гирю массой 500 г.
Дано:
Решение
Ответ. Стрелка динамометра покажет 4,9 Н.
Какая природа силы тяготения
Сила тяготения является проявлением общего закона природы, действующего во всей Вселенной закона всемирного тяготения. Открытый и сформулированный в XVII в. английским физиком Ньютоном, он утверждает, что сила гравитационного притяжения во Вселенной пропорциональна массам взаимодействующих тел и зависит от расстояния между ними.
где R — расстояние между телами, m1 и m2 — массы взаимодействующих тел, 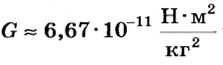
Сила тяготения, как проявление гравитационного взаимодействия Земли, является следствием взаимодействия всех тел с Землей. Поэтому в расчетах силы тяготения пользуются только массой данного тела. Характеристики Земли отображены в обобщенной форме в коэффициенте
Работа силы тяжести
Каждая сила, действующая на движущееся тело, совершает работу. Проанализируем более подробно работу, совершаемую силой тяжести. При небольших расстояниях от поверхности Земли сила тяжести постоянна и по модулю равна mg. Пусть тело массой m падает с высоты h1 до высоты h2 (рис. 132). Модуль перемещения 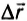
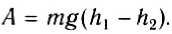
Рис. 132
Высоты h1 и h2 можно отсчитывать от любого уровня. Это может быть уровень поверхности Земли, пола класса или поверхности стола и т. д. Высоту выбранного уровня принимают равной пулю. Поэтому этот уровень называют нулевым.
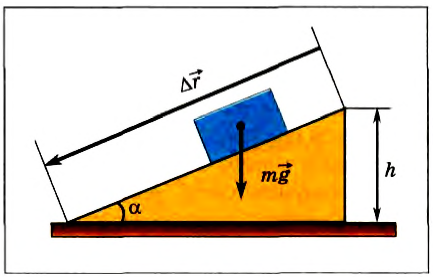
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести:
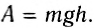
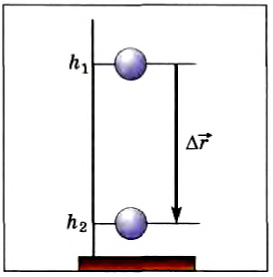
Теперь выясним, какую работу совершает сила тяжести, если тело движется не по вертикали. Для этого рассмотрим движение тела по наклонной плоскости. Пусть тело массой m совершило перемещение 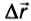
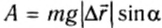
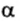
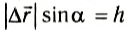
Рис. 133
Мы получили для работы силы тяжести такое же выражение, как и в случае движения тела по вертикали (см. формулу (2)). Отсюда следует, что работа силы тяжести не зависит от того, движется ли тело по вертикали или проходит более длинный путь по наклонной плоскости. Работа силы тяжести определяется только изменением высоты относительно некоторого уровня.
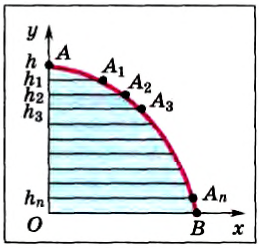
Теперь докажем, что работа силы тяжести определяется формулой (2) при движении по любой траектории. Например, некоторое тело бросили горизонтально с высоты h (рис. 134). Как известно, траекторией такого движения является парабола. Мысленно разобьем траекторию на маленькие участки 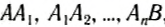
Рис. 134
Таким образом, работа силы тяжести не зависит от формы траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях тела, т. е. вычисляется но формуле (1). Отсюда следует, что если тело движется по замкнутой траектории, где начальное и конечное положения тела совпадают, то работа силы тяжести равна нулю. Такие силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положениями тела в пространстве, называются потенциальными или консервативными. Другое определение потенциальных сил: это такие силы, работа которых по замкнутой траектории равна нулю.
Для потенциальных сил можно ввести понятие потенциальной энергии. Действительно, формула (I) может быть переписана следующим образом:
A = mg(hl — h2)= -(mgh2— mgh1). (3)
Правая часть этого равенства представляет собой изменение величины mgh, взятое с противоположным знаком.
Понятие кинетической энергии, изменение которой равно работе сил, действующих на тело. Теперь мы встретились еще с одной величиной, изменение которой (но с противоположным знаком) тоже равно работе силы — в данном случае работе силы тяжести. Величину, равную mgh, называют потенциальной энергией П тела в гравитационном поле. Тогда формулу (3) можно записать в виде:
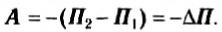
Говорят, что работа силы тяжести равна убыли потенциальной энергии тела в гравитационном поле Земли.
Если тело падает с высоты h до нулевого уровня, то работа силы тяжести равна его начальной потенциальной энергии:
Следовательно, потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты. Например, этим пользуются при забивании свай на строительных площадках (рис. 135). Чтобы поднять тело с нулевого уровня на эту же высоту, должна быть совершена работа другой силой, направленной против силы тяжести.
Рис. 135
Потенциальная энергия зависит от положения тела относительно нулевого уровня и, следовательно, от координат тела. Так как пулевой уровень может быть выбран произвольно, то и потенциальная энергия определяется неоднозначно. Однако физический смысл имеет разность потенциальных энергий тела ΔП, а эта разность не зависит от выбора нулевого уровня.
Сила тяжести является силой, с которой Земля притягивает тело. Тело обладает потенциальной энергией, потому что оно взаимодействует с Землей. Не было бы Земли, не было бы и силы притяжения, а следовательно, и потенциальной энергии тела. Поэтому потенциальная энергия — это энергия взаимодействия, в данном случае тела и Земли.
Главные выводы:
- Работа силы тяжести не зависит от формы траектории, а определяется начальным и конечным положениями тела.
- Работа силы тяжести равна нулю, если тело возвращается в исходное положение.
- Сила тяжести является потенциальной силой.
- Потенциальная энергия тела, поднятого на некоторую высоту, равна работе силы тяжести при падении тела с этой высоты.
- Потенциальная энергия — это энергия взаимодействия тел.
Сила тяжести и напряженность гравитационного поля
Как вы знаете, по современным научным представлениям взаимное притяжение между телами осуществляется посредством особого вида материи — гравитационного поля. Каждое тело вокруг себя создает гравитационное поле. Как и другие физические поля, гравитационное поле имеет свою силовую характеристику — напряженность гравитационного поля.
Напряженность гравитационного поля — это векторная физическая величина, равная отношению силы притяжения, действующей на материальную точку (тело) в гравитационном поле, к его массе:
Где 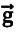
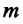
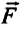
От чего зависит модуль напряженности гравитационного поля
Чтобы ответить на этот вопрос, определим модуль напряженности гравитационного поля для произвольной точки на поверхности Земли и на высоте 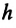
Здесь 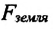
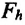
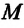
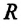
- Заказать решение задач по физике
Модуль напряженности гравитационного поля в некоторой точке прямо пропорционален массе источника данного поля и обратно пропорционален
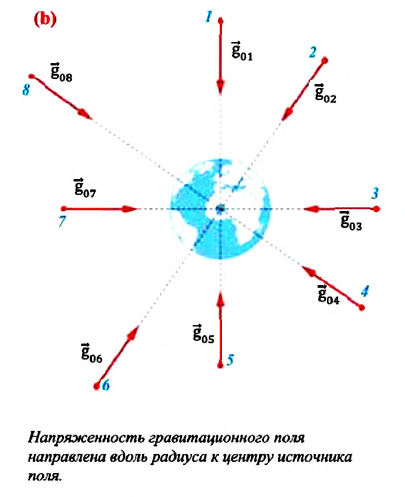
квадрату расстояния до этой точки. Модуль напряженности гравитационного поля не зависит от массы тела, помещенного в это поле. Вектор напряженности гравитационного поля в произвольной точке поля направлен вдоль радиуса к центру источника поля (b). В данной точке гравитационного поля модуль и направление напряженности гравитационного поля совпадают с модулем и направлением ускорения свободного падения.
Являются ли напряженность гравитационного поля и ускорение свободного падения одной и той же величиной
На помещенное в гравитационное поле произвольное тело действует сила притяжения со стороны источника поля. В результате тело получает ускорение (ускорение свободного падения), направленное к центру источника поля (например, центру Земли). Это ускорение сообщается телу действующей на него силой тяжести гравитационного поля.
Сила тяжести — это сила, с которой Земля (планета) притягивает тела. Сила тяжести равна произведению массы тела, помещенного в гравитационное поле Земли (планеты), на ускорение свободного падения:
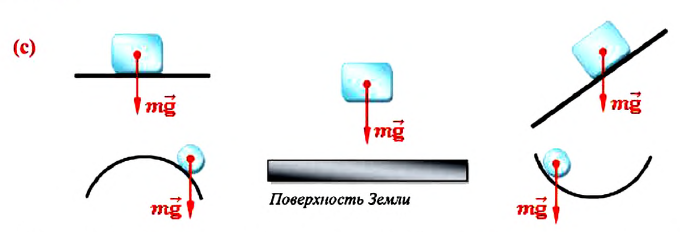
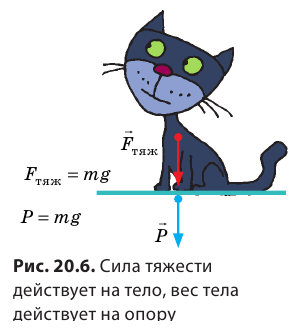
Сила тяжести всегда приложена к центру массы тела и направлена вертикально вниз (перпендикулярно к горизонтальной поверхности) к центру Земли (планеты) (с).
Из вышесказанного ясно, что понятия «напряженность гравитационного поля» и «ускорение свободного падения» имеют разный физический смысл. Так, напряженность гравитационного поля появляется в случае возникновения поля, а ускорение свободного падения возникает в результате действия силы тяжести при помещении в это поле произвольного тела (пробное тело).
Сила тяжести и вес тела
Если выпустить из рук карандаш, он обязательно упадет. Если поставить рюкзак на скамейку, она (хоть и незаметно для глаз) прогнется. Если подвесить к резиновому шнуру какое-нибудь тело, шнур растянется. Все это — следствия притяжения Земли. При этом репортажи с космических станций демонстрируют нам вроде бы «исчезновение» земного притяжения — космонавты и все вещи на борту находятся в состоянии невесомости.
Гравитационное взаимодействие:
Почему любой предмет, например выпущенный из руки карандаш, капля дождя, лист дерева и т. д., падает вниз? Почему стрела, выпущенная из лука, не летит все время прямо, а в конце концов падает на землю? Почему Луна движется вокруг Земли? Причина всех этих явлений в том, что Земля притягивает к себе все тела (рис. 20.1).
При этом все тела притягивают к себе Землю. Например, притяжение к Луне вызывает на Земле приливы и отливы (рис. 20.2). В результате притяжения к Солнцу наша планета и все другие планеты Солнечной системы движутся вокруг Солнца по определенным орбитам. В 1687 г. Исаак Ньютон сформулировал закон, согласно которому между всеми телами Вселенной существует взаимное притяжение. Такое взаимное притяжение объектов называют гравитационным взаимодействием или всемирным тяготением. Опираясь на опыты и математические расчеты, Ньютон доказал, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что всех нас притягивает Земля, и при этом мы совсем не ощущаем притяжение соседа по парте.
В физике силу гравитационного притяжения Земли, действующую на тела вблизи ее поверхности*, называют силой тяжести.
Сила тяжести 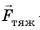
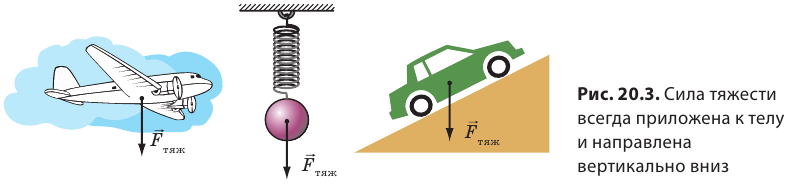
Сила тяжести приложена к телу, которое притягивается Землей, и направлена вертикально вниз, к центру Земли (рис. 20.3).
Многочисленными опытами доказано, что сила тяжести, действующая на тело, прямо пропорциональна массе этого тела: 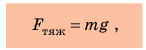
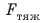
Будем считать, что, когда говорят «вблизи поверхности Земли», имеют в виду расстояние, не превышающее нескольких десятков километров.
Вблизи поверхности Земли ускорение свободного падения равно приблизительно 9,8 ньютона на килограмм: 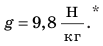
Что физики называют весом тела
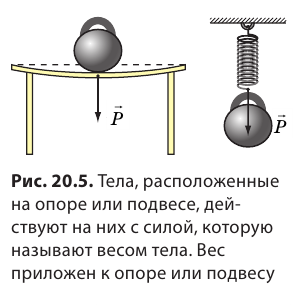
Из-за притяжения к Земле все тела сжимают или прогибают опору либо растягивают подвес. Сила, которая характеризует такое действие тел, называется весом тела (рис. 20.5).
Вес тела 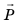
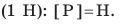
Для упрощения расчетов в случаях, когда большая точность не существенна, можно считать, что g= 10 Н/кг.
Состояние невесомости
Вы наверняка хорошо знаете термин «невесомость», но его значение многие понимают неправильно. Например, считают, что невесомость — это состояние, которое наблюдается только в космосе, где нет воздуха, или там, где отсутствует гравитация. Но это не так! Отсутствие воздуха само по себе не вызывает невесомости, а от гравитации вообще не спрячешься — во Вселенной нет ни одного уголка, где бы не действовали силы всемирного тяготения*. На самом деле невесомость — это отсутствие веса. Уберите у тела опору или подвес — и оно окажется в состоянии невесомости. (Обратите внимание: сопротивление воздуха тоже является своего рода опорой!)
Невесомость — это такое состояние тела, при котором тело не действует на опору или подвес. Тело вблизи поверхности Земли находится в состоянии невесомости, если на него действует только одна сила — сила тяжести. На короткое время невесомость легко создать и дома. Можно, например, подпрыгнуть — и вы на мгновение окажетесь в состоянии невесомости: в данном случае, пока выдвигаетесь вниз, сопротивление воздуха пренебрежимо мало и можно считать, что на вас действует только сила тяжести. Постоянно в состоянии невесомости находятся космические орбитальные станции и все, что на них находится (рис. 20.7). Это связано с тем, что космические корабли «постоянно падают» на Землю из-за ее притяжения и в то же время остаются на орбите благодаря своей огромной скорости. У нетренированного человека длительное пребывание в состоянии невесомости, как правило, сопровождается тошнотой, нарушением работы мышц, вестибулярного аппарата**, нервными расстройствами, именно поэтому космонавты проходят серьезную физическую подготовку (рис. 20.8).
Плотность материи в нашей Вселенной очень мала (2-3 атома Гидрогена на 1 м3), потому во Вселенной в среднем очень мала и гравитация. Ее называют микрогравитацией. Вестибулярный аппарат — орган чувств у людей и позвоночных животных, воспринимающий изменение положения тела в пространстве и направление движения. Этот орган отвечает, например, за способность человека различать в темноте, где верх, а где низ.
Итоги:
Во Вселенной все тела притягиваются друг к другу. Такое взаимное притяжение тел называют всемирным тяготением. Сила тяжести — сила, с которой Земля притягивает к себе тела, находящиеся на ее поверхности или вблизи нее. Сила тяжести вычисляется по формуле 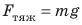
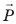
- Сила упругости в физике и закон Гука
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
- Инерция в физике
- Масса тела в физике
- Сила в физике
- Силы в механике
Целью данной статьи является подготовка к ЕГЭ по физике, мы займёмся изучением вышеперечисленных тем раздела динамики.
Сила тяжести. Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R0
Силой тяжести является сила притяжения тел к нашей планете.
Рассмотрим характеристики силы тяжести:
– Точкой приложения является центр массы тела;
– Сила тяжести направлена к центру Земли;
– Модуль силы тяжести определяют в соответствии с формулой: F тяж = gm, при этом, g = 9,8 м / с^2 – ускорение свободного падения, m – масса тела.
Сила тяжести является случаем из закона гравитационного взаимодействия, исходя из этого, ускорение свободного падения вычисляют по следующей формуле:
g = G * M3 / R3^2 = 9,8 м / с^2, здесь: g – является ускорением свободного падения, измеряется в м / с^2, G – гравитационной постоянной, обозначается в Нм^2 / кг^2, M3 – массой земли, в килограммах, R3 – радиусом Земли.
Рассмотрим примеры решения задач.
- Масса тела равна четырём килограммам. Нужно найти его силу тяжести (F).
Решение:
m = 4 кг, g = 9,8 Н / кг. Применяем следующую формулу: F тяж = gm. Подставляем в формулу значение массы: F тяж = 9,8 Н / кг * 4 кг = 40 Н.
Ответ: сила тяжести предмета равна 40 Н.
- Объём воды равен 3 дм^3.
Найти: её вес (Р).
Решение: V = 3 дм^3 = 0,003 м^3, g = 9,8 Н / кг.
Для нахождения веса воды, применяем формулу: Р = mg. Массу воды мы сможем определить при известной плотности воды.
M = p * М.
Найдём массу воды: m = 1000 кг / м^3 * 0,003 м^3 = 3 кг.
Далее находим вес воды: Р = 3 кг * 9,8 Н / кг = 29,4 Н.
Ответ: вес воды равен 29,4 Н
Сделаем выводы по данной теме:
– Ускорение свободного падения зависит от массы космического объекта;
– Ускорение свободного падения будет меньше, если расстояние до объекта будет большим.
Переходим к рассмотрению второй темы. Тема, касающаяся движения небесных тел, а также космической скорости обычно встречается в задании № 24 ЕГЭ по физике, сначала рассмотрим определения темы, далее – перейдём к решению задач.
Движение небесных тел и их искусственных спутников. Первая космическая скорость. Вторая космическая скорость.
Искусственным спутником Земли является космический аппарат, который вращается вокруг нашей планеты по орбите, называемой гелиоцентрической.
Для того, чтобы осуществлять движение по орбите вокруг планеты, у спутника должна быть определённая скорость, которая равна либо больше первой космической скорости. Спутник летает на большом расстоянии, обычно оно составляет сотни тысяч километров. Период вращения спутника по орбите составляет от нескольких часов до нескольких лет. Особое внимание уделяют спутникам, находящимся на геостационарной орбите. Это обусловлено тем, что они вращаются на протяжении одних суток.
Первой космической скорость (её также называют круговой с) является скорость, необходимую для объекта, не имеющего двигатель. Такой вид скорости является минимальным, при ней движущееся в горизонтальном направлении тело, не будет падать, оно будет продолжать движение по орбите.
Формула для определения этой скорости: U1 = √G * (M / R).
Второй космической скоростью (её также называют параболической либо скоростью убегания) является минимальная скорость, необходимая для объекта. Считают, что после того, как тело приобретёт эту скорость, оно перестаёт получать негравитационное ускорение.
Формула для нахождения данной скорости = √2G * (M / R).
Решим задачи по этой теме.
- Масса Солнца равна 2 * 1030 кг, его диаметр= 1,4 * 109 м.
Найти: первую космическую скорость Солнца.
Решение: известно, что спутник движется в соответствии с силой тяготения. Применяем второй закон Ньютона, получается: mv1^2 / Rc = G mM / Rc^2.
Далее: u1 = √ GM / Rc = 437 км / с.
Ответ: первая космическая скорость Солнца приблизительно равна 437 км /с.
- Период обращения Сатурна вокруг Солнца составляет 29,5 лет. Масса Солнца составляет 2 * 1030 кг.
Найти: расстояние от Сатурна до Солнца (расстояние должно быть средним).
Решение: известно, что рассматриваемая планета движется по орбите Солнца. Используем второй закон Ньютона: mv^2 / r = G mMc / r^2, здесь: m – является массой Сатурна, r – расстоянием от планеты Сатурн к Солнцу, Мс – масса Солнца.
Период обращения Сатурна вычислим по формуле: Т = 2пr / u, получается: u = 2 пr / T.
Подставляем выражение в уравнение, получается: (2пr / T)^2 = G Mc / r.
Находим расстояние от Сатурна до Солнца: r = 3 √ GM cT^2 / 4п^2 = 1,42 * 10^12 м.
Ответ: 1,42 * 10^12 м.
В ходе подготовке к экзамену рекомендуем просмотреть демонстрационные варианты ЕГЭ по физике, так вы сможете понять примерную формулировку и тему заданий.
Сила трения. Сухое трение. Сила трения покоя. Коэффициент трения.
Переходим к рассмотрению следующей темы – сила трения, сухое трение.
Трение определяют как один из видов взаимодействия среди тел.
Внешним является трение, в ходе которого тела взаимодействуют с помощью своих поверхностей.
Внутренним трением называют движущиеся жидкости и газы.
У силы трения существуют определённые характеристики:
– Направление силы трения – противоположная сторона равнодействующей силы;
– Точкой приложения силы трения располагается на плоскости поверхностей, которые соприкасаются;
– Существует определённая формула, по которой находят модуль силы трения: F mp = μN, здесь: F mp – является силой трения скольжения, μ – коэффициентом трения, N – силой реакции опоры.
N – рассматривают, как силу, реагирующую с опорой на вес тела, а также одну из видов сил. Коэффициент трения находят в соответствующих таблицах.
Сила трения скольжения.
Сухим трением является взаимодействие, которое возникает при касании тел, при этом, между данными телами не должно быть газов и жидкостей.
Существуют несколько видов сухого трения:
– Скольжение;
– Покоя;
– Качения.
Силой трения покоя называют силу, препятствующую движению тел. Эту силу принять считать наибольшей.
Сила трения скольжения появляется в момент преодоления силы покоя. При этом коэффициенты силы трения должны уменьшаться. Для беспрепятственного скольжения следует полировать поверхность. Следует иметь в виду, что при полном устранении неровностей поверхности, коэффициент трения будет возрастать (это происходит по причине сближения молекул тела).
Сила трения качения является наиболее малой по сравнению с другими видами сил. Примером является тумба на колёсах, её горазда легче передвинуть, чем тумбу на опоре.
Существует определённый коэффициент трения. Им является характеристика трения в качестве давления.
Коэффициент трения находят по формуле: F tr = μN.
Коэффициент не имеет зависимости от площадей поверхностей, которые соприкасаются.
В некоторых случаях коэффициент трения заменяют углом трения.
Рассмотрим задачу по данной теме.
Бревно, у которого масса составляет пять килограммов, скользит по поверхности, являющейся горизонтальной. Известно, что сила трения скольжения = 20Н.
Найти: силу трения, при условии, что масса бревна будет меньше в два раза.
Решение: F mp = μN. N = mg. N1 = mg / 2 = N / 2, далее: F mp1 = F mp / 2 = 20 Н / 2 = 10 Н.
Ответ: сила трения равна 10 Н.
Рассмотрим ещё одну небольшую тему, встречающую в разделе динамики ЕГЭ по физике, это тема давления.
Давление
Давлением называют силу, которая приходится на определённую площадь поверхности.
Давление измеряется в Паскалях. Давление принято измерять в миллиметрах ртутного столба, а большое давление – в атмосферах или барах. Относительным атмосферным давлением считают 10^5 Па, или 760 миллиметров ртутного столба.
Таким образом, мы завершили рассмотрение тем из раздела динамики, встречающиеся в КИМах ЕГЭ по физике, изучили основные определения, характеристики, а также решили задачи.

Разбираетесь с такой физической категорией, как сила тяжести? Формула, ее составляющие и единицы измерения укажут, что сильнее притянет Земля — яблоко или поезд. Отличается ли сила тяжести от силы тяготения? Объясним, как не перепутать эти две величины.
Что такое сила тяжести
Каждый день наблюдаем, как тела вокруг деформируются (меняют форму или размеры), ускоряются или тормозят, падают. В реальной жизни с различными телами происходят самые разнообразные вещи. Причина всех действий и взаимодействий кроется в некой силе. О чем идет речь?
Понятие силы
Силой называют физическую векторную величину, которая оказывает воздействие на тело, а ее источниками становятся другие тела. Что означает понятие векторной величины? Это говорит о том, что сила наделена направлением. В зависимости от того, куда она направлена, можно получить разные результаты.
Это как если стоять на вершине горы на сноуборде, то от направления толчка будет зависеть дальнейшее движение. Таков результат приложения силы в этом случае. Силы, которые изучают ученые-физики, разнообразны и очень важны для нашей повседневной жизни.
Определение и значение силы тяжести
Одна из них носит название сила тяжести. Физика предлагает следующее определение: сила тяжести — это величина, которая показывает, насколько сильно Земля притягивает тело, которое расположено на ее поверхности или рядом с ней. Таким образом, направление этой силы — центр нашей планеты.
Сила тяжести на Земле крайне важна по следующим причинам:
- Наша планета притягивает все, что попадает в сферу действия этой силы, будь то твердое тело, жидкость или газ.
- Благодаря ее существованию стало возможным создание атмосферы (молекулы газов, которые ее составляют, не улетают в космические просторы), появились и остаются на своих местах моря и океаны.
- Любой предмет, который приподнимаем и роняем, обязательно упадет вниз по направлению к Земле.
Кстати, именно из-за воздействия этой силы люди не могут летать. Самостоятельно развить скорость, на которой полет становится возможным (так называемую первую космическую) человек не способен, а потому в обычной жизни всегда твердо стоит ногами на Земле.
Сила тяжести и сила тяготения: отличия
Сила тяжести, определение которой дали выше, схожа с силой тяготения. Оба варианта связывает сила притяжения.
Однако эти две силы не одно и то же, хоть их и часто путают. Давайте разберемся, в чем тут дело.
Еще в 1682 году Исаак Ньютон открыл закон о всемирном тяготении. Сформулирован он был так: тела притягивают друг друга, а сила этого тяготения — величина, прямо пропорциональная произведению их масс и обратно пропорциональна расстоянию, возведенному в квадрат.
Математически силу тяготения записывают так: F = G×M×m/R², где:
- F — сила тяготения, Н;
- M — масса первого тела (часто планеты), кг;
- m — масса второго тела, кг;
- R — дистанция между ними, м;
- G — постоянная величина (G = 6,67×10⁻¹¹ м³×кг⁻¹×с⁻²).
Продемонстрировать эту силу легко — достаточно встать на весы. Стрелка сразу же отклонится, показывая вес тела. Так происходит из-за очень большой массы Земли, благодаря которой мы придавлены к ней. На Луне, масса которой меньше, вес человека меньше в несколько раз.
Итак, закон о всемирном тяготении и соответствующая сила необходимы для вычисления силы взаимодействий между разнообразными телами. При этом их размеры должны быть меньше, чем расстояние между ними.
Теперь вернемся к нашей теме и рассмотрим подробно, что же такое сила тяжести, обозначение которой дали выше, и как она связана с силой тяготения.
Сила тяжести: формула, единицы измерения
Напомним, что когда говорим о силе тяжести, то имеем в виду силу, с которой осуществляет притяжение наша планета.
Формула силы тяжести такова: F = m×g, где:
- F — сила тяжести, Н;
- m — масса тела, кг;
- g — ускорение свободного падения, м/с².
В этой формуле видим новую величину — ускорение свободного падения. Так называют ускорение, которое приобретает тело рядом с Землей во время свободного и беспрепятственного падения. Рядом с поверхностью Земли значение этой величины примерно равняется 9,81 м/с², а в приблизительных расчетах используют округленное значение 10 м/с².
По этой формуле рассчитывается сила тяжести, единица измерения которой — Ньютоны (в честь Исаака Ньютона).
Чему равна сила тяжести? Глядя на эту формулу, можно сказать, что сила тяжести схожа с весом тела. В покое на Земле эта величина и вес будут идентичны. Но это не одно и то же. Почему? Объяснение не сложное:
- Силой, с которой на тела действует Земля, называют силу тяжести.
- Вес тоже сила, с которой тела действуют на опору.
- То есть у них отличаются точки действия: первая направлена на центр массы тел, а вес направлен на опору.
Кроме того, на величину силы тяжести влияет масса и планета, на которой проводятся измерения. Вес определяется также ускорением, с которым происходит движение тела и опоры.
К примеру, вес тела в лифте определяется тем, в каком направлении и как быстро происходит движение тела. Сила тяжести не учитывает, куда и что движется: эти внешние факторы на нее не влияют.
Итак, с весом разобрались. А что же с силой тяготения, которую упоминали выше? Можем ли две эти силы приравнять? На этот раз ответ будет утвердительным. Но только, когда мы говорим о Земле и теле, которое к ней притягивается. В этом случае обе силы будут равны.
Выразим это математически:
- F = m×g.
- F = G×M×m/R².
- m×g = G×M×m/R².
Если обе части полученного уравнения разделить на массу, то получим такую формулу: g = G×M/R².
Величина g (ускорение свободного падения) уникальна для каждой планеты:
- На нашей Земле свободно падающее тело с каждой секундой ускоряется примерно на 9,81 метр (м/с²).
- Ускорение свободного падения рядом с Луной имеет величину всего 1,62 м/с².
- На Юпитере это значение достигает 26,2 м/с². Человек, который весит 60 кг, на этой планете почувствует себя так, будто бы поправился на 100 кг.
Как изменится величина, если тело будет падать 4 секунды? Попробуем подсчитать:
- Скорость падения в начальной точке составит 0 м/с².
- В течение первой секунды она увеличится до 9,81 м/с².
- За вторую секунду величина вырастет вдвое и составит 19,62 м/с².
- Третья секунда добавить еще одну величину ускорения и получится 29,43 м/с².
- В четвертую секунду скорость движения тела достигнет 39,24 м/с², что равняется приблизительно 141 км/ч.
Отметим, что яблоко и кирпич будут падать с равной скоростью. Только очень легкие предметы во время падения замедляет воздух, оказывая им ощутимое сопротивление. Так, птичье перышко будет совершать падение очень медленно и плавно.
Задумываемся об этом или нет, на каждого из нас оказывает воздействие сила тяжести. Формула ее расчета состоит из массы, умноженной на величину ускорения свободного падения. Эта сила показывает воздействие планет на тела, которые находятся рядом с их поверхностями. Поэтому ее величина отличается на Земле и на Луне.
Оригинал статьи: https://www.nur.kz/family/school/1909020-sila-tyazhesti-formula-edinitsy-izmereniya-osobennosti/
Видеоурок: Закон всемирного тяготения
Лекция: Закон всемирного тяготения. Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты

До некоторого времени Ньютон не задумывался о том, что его предположения справедливы для всех тех, находящихся во Вселенной. Спустя некоторое время им были изучены законы Кеплера, а также законы, которых придерживаются тела, что свободно падают на поверхность Земли. Данные мысли не были зафиксированы на бумаге, а только остались заметки про яблоко, упавшее на Землю, а также о Луне, которая вращается вокруг планеты. Он считал, что
-
все тела рано или поздно упадут на Землю;
-
они падают с одинаковым ускорением;
-
Луна двигается по окружности с постоянным периодом;
-
размеры Луны практически в 60 раз меньше, чем у Земли.
В результате всего это был сделан вывод, что все тела притягиваются друг к другу. При этом, чем больше масса тела, тем с большей силой оно притягивает к себе окружающие объекты.
В результате этого был открыт закон всемирного притяжения:
Любые материальные точки притягиваются друг к другу с силой, увеличивающейся в зависимости от роста их масс, но при этом уменьшается в квадратной пропорциональности в зависимости от расстояния между этими телами.
F – сила гравитационного притяжения
m1, m2 – массы взаимодействующих тел, кг
r – расстояние между телами (центрами масс тел), м
G – коэффициент (гравитационная постоянная) ≈ 6,67*10-11 Нм2/кг2

Коэффициент пропорциональности из закона всемирного тяготения был определен экспериментальным путем ученым Г.Кавендишем. Гравитационная постоянная равна силе, с которой притягиваются килограммовые тела на расстоянии одного метра:
G = 6,67*10-11 Нм2/кг2
Взаимное притяжение тел объясняется гравитационным полем, подобным электрическому, которое находится вокруг всех тел.

Вокруг Земли также существует такое поле, его еще называют полем земного притяжения. Все тела, что находятся в местах его действия, притягиваются к Земле.
Сила тяжести — это равнодействующая гравитационной силы, а также центростремительной силы, направленной по оси вращения.

Характеристика силы тяжести:
1. Точка приложения: центр масс тела.
2. Направление: к центру Земли.
3. Модуль силы определяется по формуле:
Fтяж = gm
g = 9,8 м/с2 — ускорение свободного падения
m — масса тела
Так как сила тяжести — это частный случай закона гравитационного взаимодействия, то ускорение свободного падения определяется по формуле:
g — ускорение свободного падения, м/с2
G — гравитационная постоянная, Нм2/кг2
M3 — масса Земли, кг
R3 — радиус Земли
Из этого можно сделать
вывод:
-
чем больше масса космического объекта, тем больше ускорение свободного падения;
-
чем больше расстояние до космического объекта, тем меньше ускорение свободного падения.
Более того, на данную величину влияет и период вращения планеты вокруг оси.
Если тело находится на некотором расстоянии от поверхности Земли, то определить ускорение можно по следующей формуле:
Если же с увеличением высоты уменьшается ускорение, то можно сделать вывод, что сила тяжести так же уменьшается.