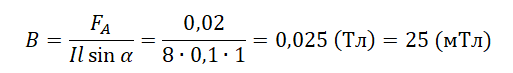Сила Ампера — сила, которая действует на проводник с током, помещенный в магнитное поле.
Модуль силы Ампера обозначается как FA. Единица измерения — Ньютон (Н).
Математически модуль силы Ампера определяется как произведение модуля вектора магнитной индукции B, силы тока I, длины проводника l и синуса угла α между условным направлением тока и вектором магнитной индукции:
FA=BIlsinα
Максимальное значение сила Ампера принимает, когда ток в проводнике направлен перпендикулярно вектору магнитной индукции, так как sin90°=1. И сила Ампера отсутствует совсем, если ток в проводнике направлен относительно вектора магнитной индукции вдоль одной линии. В этом случае угол между ними равен 0, а sin0°=1.
Пример №1. Максимальная сила, действующая в однородном магнитном поле на проводник с током длиной 10 см, равна 0,02 Н. Сила тока в проводнике равна 8 А. Найдите модуль вектора магнитной индукции этого поля.
10 см = 0,1 м
Так как речь идет о максимальной силе, действующей на проводник с током, тоsinα при этом равен 1 (проводник с током расположен перпендикулярно вектору магнитной индукции).
Определение направления силы Ампера
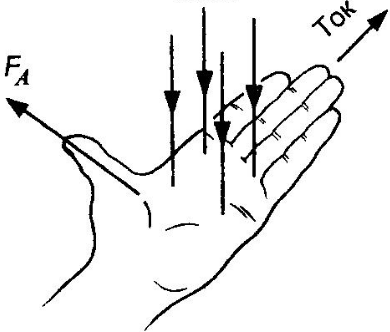
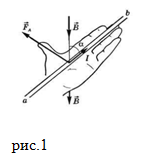
Направление вектора силы Ампера определяется правилом левой руки.
Правило левой руки
Если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции →B входила в ладонь, то отогнутый на 90 градусов большой палец покажет направление силы, действующий на отрезок проводника (направление силы Ампера).
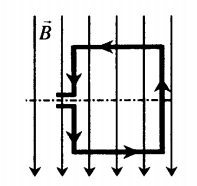
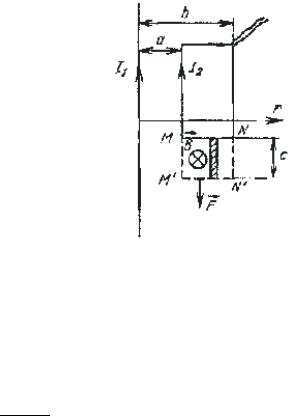
Пример №2. В однородном магнитном поле находится рамка, по которой начинает течь ток (см. рисунок). Какое направление (вверх, вниз, влево, вправо, от наблюдателя, наблюдателю) имеет сила, действующая на нижнюю сторону рамки?
Так как в нижней стороне рамки ток направлен вправо, то четыре пальца левой руки нужно направить вправо. Саму левую руку при этом нужно расположить перпендикулярно плоскости рисунка ладонью вверх, чтобы в нее входили линии вектора магнитной индукции. Если отогнуть большой палец на прямой угол, то он покажет направление силы Ампера, действующей на нижнюю часть рамки. В данном случае она направлена в сторону от наблюдателя.
Работа силы Ампера
Проводники, на которые действует сила Ампера, могут перемещаться под действием этой силы. В этом случае говорят, что сила Ампера совершает работу. Из курса механики вспомним, что работа равна:
A=Fscosα
F — сила, совершающая работу, s — перемещение, совершенное телом под действием этой силы, α — угол между вектором силы и вектором перемещения.
Отсюда работа, совершаемая силой Ампера, равна:
A=FAscosα=BIlsinβscosα
α — угол между вектором силы и вектором перемещения, β — угол между условным направлением тока и вектором магнитной индукции.
Пример №3. Проводник длиной l = 0,15 м перпендикулярен вектору магнитной индукции однородного магнитного поля, модуль которого B = 0,4 Тл. Сила тока в проводнике I = 8 А. Найдите работу, которая была совершена при перемещении проводника на 0,025 м по направлению действия силы Ампера.
Так как проводник расположен перпендикулярно вектору магнитной индукции, и поле однородно, то синус угла между ними равен «1». Так как направление перемещение проводника совпадает с направлением действия силы Ампера, то косинус угла между ними тоже равен «1». Поэтому формула для вычисления работы силы Ампера принимает вид:
A=BIls
Подставим известные данные:
A=0,4·8·0,15·0,025=0,012 (Дж)=12 (мДж)
Задание EF17704
а) вверх
б) вниз
в) к нам
г) от нас
Алгоритм решения
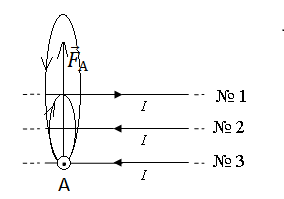
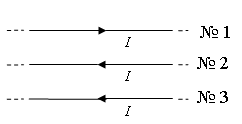
1.Определить направление вектора результирующей магнитной индукции первого и второго проводников в любой точке третьего проводника.
2.Используя правило левой руки, определить направление силы Ампера, действующей на третий проводник со стороны первых двух проводников.
Решение
На третьем проводнике выберем произвольную точку и определим, в какую сторону в ней направлен результирующий вектор →B, равный геометрической сумме векторов магнитной индукции первого и второго проводников (→B1и →B2). Применим правило буравчика. Мысленно сопоставим острие буравчика с направлением тока в первом проводнике. Тогда направление вращения его ручки покажем, что силовые линии вокруг проводника 1 направляются относительно плоскости рисунка против хода часовой стрелки. Ток во втором проводнике направлен противоположно току в первом. Следовательно, его силовые линии направлены относительно плоскости рисунка по часовой стрелке.
В точке А вектор →B1 направлен в сторону от наблюдателя, а вектор →B2— к наблюдателю. Так как второй проводник расположен ближе к третьему, создаваемое им магнитное поле в точке А более сильное (силы тока во всех проводниках равны по условию задачи). Следовательно, результирующий вектор →B направлен к наблюдателю.
Теперь применим правило левой руки. Расположим ее так, чтобы четыре пальца были направлены в сторону течения тока в третьем проводнике. Ладонь расположим так, чтобы результирующий вектор →B входил в ладонь. Теперь отставим большой палец на 90 градусов. Относительно рисунка он покажет «вверх». Следовательно, сила Ампера →FА, действующая на третий проводник, направлена вверх.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18417
Чему равна сила Ампера, действующая на стальной прямой проводник с током длиной 10 см и площадью поперечного сечения 2⋅10–2 мм2 , если напряжение на нём 2,4 В, а модуль вектора магнитной индукции 1 Тл? Вектор магнитной индукции перпендикулярен проводнику. Удельное сопротивление стали 0,12 Ом⋅мм2/м.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать формулу для определения силы Ампера.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина проводника: l = 10 см.
• Площадь поперечного сечения проводника: S = 2⋅10–2 мм2.
• Напряжение в проводнике: U = 2,4 В.
• Модуль вектора магнитной индукции: B = 1 Тл.
• Удельное сопротивление стали: r = 0,12 Ом⋅мм2/м.
• Угол между проводником с током и вектором магнитной индукции: α = 90о.
10 см = 0,1 м
Сила Ампера определяется формулой:
FA=BIlsinα
Так как α = 90о, синус равен 1. Тогда сила Ампера равна:
FA=BIl
Силу тока можно выразить из закона Ома:
I=UR
Сопротивление проводника вычисляется по формуле:
R=rlS
Тогда сила тока равна:
I=USrl
Конечная формула для силы Ампера принимает вид:
FA=BlUSrl=BUSr=1·2,4·2·10−20,12=0,4 (Н)
Ответ: 0,4
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17725
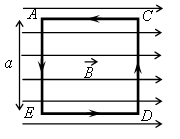
Алгоритм решения
1.Сделать список известных данных.
2.Определить, при каком условии рамка с током будет вращаться вокруг стороны CD.
3.Выполнить решение в общем виде.
Решение
По условию задачи известными данными являются:
• Сторона квадратной рамки с током: a.
• Вектор магнитной индукции однородного горизонтального магнитного поля, в котором лежит рамка: B.
Пусть по рамке течёт ток I. На стороны АЕ и CD будут действовать силы Ампера:
FA1=FA2=IaB
Для того чтобы рамка начала поворачиваться вокруг оси CD, вращательный момент сил, действующих на рамку и направленных вверх, должен быть не меньше суммарного момента сил, направленных вниз. Момент силы Ампера относительно оси, проходящей через сторону CD:
MA=Ia2B
Момент силы тяжести относительно оси CD:
Mmg=−12mga
Чтобы рамка с током оторвалась от горизонтальной поверхности, нужно чтобы суммарный момент сил был больше нуля:
MA+Mmg>0
Так как момент силы тяжести относительно оси CD отрицательный, это неравенство можно записать в виде:
Ia2B>12mga
Отсюда выразим силу тока:
I>mga2a2B
I>mg2aB
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.8k
Работ сил Ампера A = IΔΦ. Здесь ΔΦ имеет смысл модуля магнитного потока сквозь поверхность, заметённую проводником с постоянным током I при его перемещении: ΔΦ = |Φзам|. Знак работы определяется по направлению движения проводника (см. пример 8.1). ΔΦ имеет также смысл изменения магнитного потока Φ сквозь поверхность, натянутую на контур с постоянным током, при его перемещении: ΔΦ = Φкон – Φнач.
Примеры решения задач
Пример8.1
В одной плоскости с длинным* прямым проводником, по которому идёт ток I1 = 10 А, находится плоская прямоугольная рамка. Длинные стороны рамки
|
параллельны проводу, расстояния от них до провода |
a = 5 см, |
||
|
b = 10 см. По рамке протекает ток I1 = 2 А, его направление |
в |
||
|
ближайшей длинной стороне совпадает с направлением |
тока в |
||
|
проводе. Рамка может растягиваться за счёт перемещения |
её короткой |
||
|
стороны MN параллельно самой себе. Найти работу сил |
Ампера при |
||
|
удлинении рамки на c = 2,0 см. |
|||
|
При перемещении стороны рамки MN она заметает |
площадь S в |
||
|
виде прямоугольника MNM’N’ (рис. 8.1). Работа сил Ампера |
равна |
||
|
A = I2|Φзам|, где Φзам – магнитный поток через площадь S |
|||
|
зам = ∫S BdS . |
|||
|
по |
|||
|
Направление B – магнитной индукции, созданной |
проводом с |
||
|
током – от нас в пределах площади S, B = μ0I/(2πr), где r – |
Рис. 8.1 |
расстояние |
|
|
от прямого провода (см. пример 6.2). |
Вектор dS параллелен B , а так как нас интересует |Φзам|, направим его коллинеарно B . Тогда
BdS = BdS . Модуль dS – это площадь бесконечно малого участка площади S прямоугольника, в пределах которого магнитную индукцию B можно считать постоянной. Эти участки представляют собой прямоугольники бесконечно малой ширины dr и высоты c и показаны на рис. 8.1, dS = cdr. Тогда
|
Φзам |
a |
2 |
2 |
ln |
||
|
b |
μ I cdr |
μ I c |
b |
|||
|
= ∫ |
0 πr1 |
= 0πr1 |
a |
, |
||
где пределы интегрирования соответствуют положению на оси r длинный сторон прямоугольника. Работа
|
A= 2πr0 |
I1I2cln a =2,8 10−6 |
Дж. |
|
|
μ |
b |
Сила Ампера F , действующая на рассматриваемую сторону, направлена в сторону перемещения рамки (рис. 8.1), следовательно, её работа положительна.
Задачи
8.1.Квадратная рамка со стороной a = 20 см помещена в однородное магнитное поле с магнитной индукцией B = 0,040 Тл. Нормаль к плоскости рамки составляет угол α = 60° с направлением вектора магнитной индукции. Найти магнитный поток, пронизывающий рамку.
8.2.Обмотка соленоида длиной l = 1,0 м и радиусом r = 25 мм содержит n = 11 витков/см, обтекаемых током I = 2,0 А. Считая, что витки плотно прилегают друг к другу, найти потокосцепление соленоида.
8.3. Обмотка тора (кольцевого соленоида) квадратного сечения со стороной a = 4 см состоит из N = 1000 витков, по которым идет ток I = 2,0 А. Внутренний радиус тора r1 = 8 см. Найти магнитный поток внутри тора.
65
8.4.По длинному* медному проводу кругового сечения идет ток I = 10 А. Плотность тока постоянна, относительная магнитная проницаемость меди μ = 1. Найти магнитный поток, приходящийся на единицу длины, в пределах самого провода.
8.5.Ток I = 5 А течёт по внутреннему медному проводу длинного* коаксиального кабеля и
возвращается по его внешней металлической оболочке. Диаметр внутреннего провода d1 = 2 мм, внешней оболочки – d2 = 10 мм. Найти магнитный поток, приходящийся на единицу длины кабеля. Плотность тока во внутреннем проводе постоянна по сечению.
8.6.Прямоугольная рамка со сторонами a = 10 см и b = 5 см лежит в одной плоскости с длинным* прямым проводом, по которому идет ток I = 10 А. Длинные стороны рамки параллельны проводу,
ближайшая сторона находится на расстоянии x1 = 5 см от прямого проводника. Рамка, оставаясь в той же плоскости, перемещается параллельно самой себе, удаляясь от прямого провода так, что
кратчайшее расстояние между ними возрастает до x2 = 10 см. Найти изменение магнитного потока, пронизывающего рамку, если ток, обтекающий рамку, по стороне, ближайшей к проводу, направлен: а) так же, как ток I; б) противоположно току I.
8.7.В однородном магнитном поле с индукцией B = 2,0·10–5 Тл в плоскости, перпендикулярной линиям индукции, проложены длинные* параллельные шины. Шины соединены подвижным проводником, длина которого l = 0,5 м равна расстоянию между ними. При токе I = 5 А проводник под действием силы Ампера перемещается на расстояние x = 4,0 см. Найти работу силы Ампера при этом перемещении. Ток в цепи считать постоянным.
8.8.Два параллельных достаточно длинных* провода находятся на расстоянии h1 = 2 см друг от друга. По проводам идут токи I1 = I2 = 2,0 А взаимно противоположного направления. Какую работу на единицу длины проводов совершают силы Ампера при медленном удалении проводов друг от друга до расстояния h2 = 8 см?
8.9.В плоскости, перпендикулярной линиям индукции однородного магнитного поля с индукцией B = 3,0·10–5 Тл лежит тонкое* кольцо, радиус которого r = 5 см. По кольцу идёт ток I = 1,5 А.
1. Каково должно быть направление тока в кольце, чтобы работа внешних сил при повороте кольца вокруг его диаметра на 180° была положительной?
2. Какую работу совершат внешние силы при этом повороте?
8.10.В однородном магнитном поле с индукцией B = 2,0·10–5 Тл помещена квадратная рамка со
стороной a = 10 см, обтекаемая током I = 1,0 А. Магнитный момент рамки параллелен B . Какую работу совершают силы Ампера при медленном повороте рамки вокруг одной из её сторон на угол
α = 90°; 180°; 360°?
8.11. В одной плоскости с длинным* прямым проводом, по которому идёт ток I1 = 10 А, находится плоская прямоугольная рамка со сторонами a = 10 см, b = 7,5 см. Длинные стороны рамки параллельны прямому проводу, расстояние от него до ближайшей длинной стороны рамки x0 = 2,5 см. По рамке идет ток I2 = 1,0 А. В стороне, ближайшей к прямому проводу, ток I2 направлен противоположно току I1. Рассчитать, какую работу совершат силы Ампера при медленном повороте рамки на угол α = 180°: а) вокруг оси, параллельной прямому проводу и проходящей через середину рамки; б) вокруг оси, совпадающей с длинной стороной, ближайшей к прямому проводу.
8.12. В одной плоскости с длинным* прямым проводом, по которому идёт ток I1 = 10 А, находится прямоугольная рамка со сторонами a = 5 см, b = 10 см. Длинные стороны рамки параллельны прямому проводу и ближайшая отстоит от него на расстояние x1 = 5 см. Рамка обтекается током I2 = 3 А, в прямом проводнике и ближайшей к нему стороне рамки токи направлены одинаково. Какую работу совершают внешние силы при поступательном прямолинейном перемещении рамки в её плоскости в направлении нормали к проводу? Конечное расстояние от прямого провода до ближайшей к нему длинной стороны рамки x2 = 10 см.
8.13. В длинный* соленоид вдоль его оси медленно втягивается маленькая* плоская рамка. Обмотка рамки состоит из N = 10 витков площадью S = 2,0 см2 каждый. Ток в обмотке рамки I1 = 1,0 А. Обмотка
66
соленоида содержит n = 100 витков/см, по которым идёт ток I2 = 5 А. Какую работу совершают силы Ампера при перемещении рамки из середины основания соленоида в середину его оси? Плоскость рамки нормальна к оси соленоида, токи I1 и I2 направлены одинаково.
8.14.Маленькая* квадратная рамка из мягкой проволоки со стороной a = 3,0 см, обтекаемая током
I1 = 0,10 А, медленно втягивается в середину длинного* соленоида. Обмотка соленоида состоит из n = 10 витков/см, ток в соленоиде I = 1,0 А. Перемещение рамки происходит вдоль оси соленоида, её плоскость всё время перпендикулярна оси соленоида. Токи в соленоиде и в рамке направлены одинаково. Найти суммарную работу, совершенную силами Ампера при перемещении рамки из середины основания до середины оси и при деформации рамки, если диаметр соленоида D >> a.
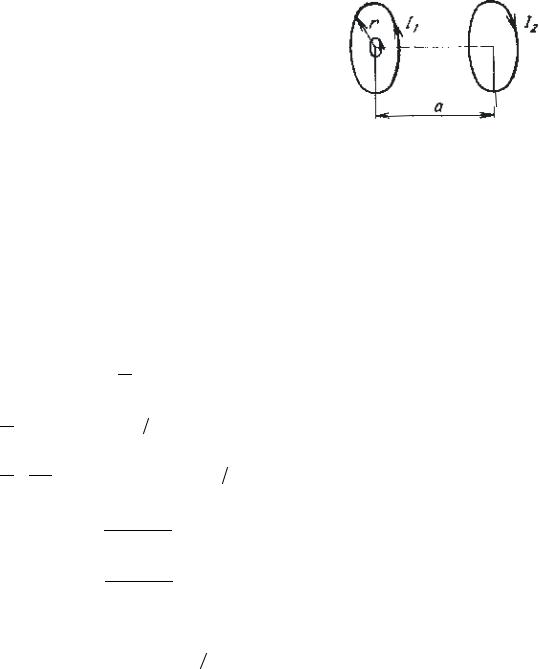
8.15.Два плоских круглых витка радиуса r = 10 см каждый расположены параллельно друг другу на расстоянии a = 10 см, причём прямая, соединяющая центры витков, перпендикулярна плоскостям обоих витков. По виткам протекают токи
|
взаимопротивоположных направлений, но одинаковые |
по величине |
||
|
I1 = I2 = 2,0 А. Концентрично первому витку расположен |
маленький |
||
|
виток площадью S = 0,20 см2. По витку течёт ток I = 0,10 А, |
|||
|
направленный так же, как ток I1 (рис. 8.2). Какую работу |
должны |
||
|
совершить внешние силы, чтобы переместить маленький |
виток |
||
|
(параллельно самомусебе) в середину второго витка? |
|||
|
8.16. Две тонкие катушки с током, векторы магнитных |
Рис. 8.2 |
моментов |
|
которых коллинеарны и по модулю равны соответственно pm1 = 8·10–2 А·м2 и pm2 = 0,12 А·м2, удалены друг от друга на расстояние x1 = 1,0 м. Расстояние между центрами катушек x1 >> l, где l – длина каждой катушки. Найти: а) работу, которую совершат внешние силы, чтобы увеличить расстояние
|
между |
центрами |
катушек |
до |
x2 = 1,1 м; |
|
б) силу взаимодействия катушек на расстоянии x1. |
Ответы
|
8.1. |
= Ba |
α = |
|
|
8.2. |
= μ0πn r lI = |
8.3.Φ= 2μ0 NIaln 1+ a =6,5 10−6 Вб.
πr1
8.4.= μ40I =1,0 10−6 Вб м. l π
8.5.= μ40I 1 +2ln d2 =2,1 10−6 Вб м. l π d1
8.6.а) ΔΦ= 2μ0 Ialn x1 (x2 +b)= −5,8 10−8 Вб;
πx2 (x1 +b)
|
ΔΦ |
μ |
ln |
−1 |
( |
2 |
+b |
) |
5,8 10 Вб |
|||||||||
|
( |
) |
||||||||||||||||
|
x |
x |
||||||||||||||||
|
б) |
= π0 Ia |
x2 |
x1 |
+b |
= |
−8 . |
|||||||||||
|
8.7. |
A |
= IBlx |
= |
. |
|||||||||||||
|
8.8. |
l |
= |
π0 |
I1I2 ln h12 |
=1,1 10−6 Дж м. |
||||||||||||
|
A |
μ |
h |
|||||||||||||||
|
n0 |
2 |
− |
|||||||||||||||
|
8.9. 1. |
↑↑B . |
||||||||||||||||
|
2. |
A′= |
πBIr |
= |
. |
A2 = − BIa = − − |
||||||||||||
|
8.10. |
A1 = −BIa |
= − |
− |
; |
; A3 = 0. |
67

8.11.а) A = μ0 I1I2aln 1 + b0 =5,5 10−7 Дж;
πx
|
б) A = |
π0 |
I1I2aln b− x0 |
=1,4 10−7 Дж. |
|||||||||||||||||
|
μ |
b+ x |
|||||||||||||||||||
|
μ |
2 |
2 |
ln |
(x |
( |
+a)0 x |
1,7 |
10 |
− |
Дж |
||||||||||
|
8.12. |
A′= |
μ2 |
1 |
b |
x |
1 |
2 |
− |
) |
7 |
. |
|||||||||
|
π0 |
I I |
1 x |
+a2 = |
|||||||||||||||||
|
8.13. |
A = |
0 I1I2NnS =6 10 5 Дж. |
8 |
Дж |
||||||||||||||||
|
0 1 |
2 |
2 |
π |
2 |
8,7 |
10 |
||||||||||||||
|
8.14. |
A = |
μ2I I na |
− |
= |
− |
. |
||||||||||||||
|
8.15. |
A = μ I I |
S |
− |
1 |
+ a2 |
− |
|||||
|
0 1 |
r |
1 |
1 |
r2 |
2 |
||||||
|
2 |
|||||||||||
|
μ |
1 |
pm |
2 |
3 |
− x |
3 |
|||||
|
8.16. |
а) A = π0 pm |
x |

=4,8 10−10 Дж.
|
б) F = π0 |
mx14 m2 |
=5,8 10−9 Н. |
|
2 |
1 |
|
|
μ |
p p |
68
Соседние файлы в папке 3 — практ_зан
- #
- #
Закон Ампера
Элементарная сила Ампера ($dbar{F}_A$) определена законом (или формулой) Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(1)$$
где I – сила тока, $d bar{l}$ – малый элемент длины проводника – это вектор, равный по модулю длине проводника, направленный в таком же направлении как вектор плотности тока, $bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d bar{F}_{A}=bar{j} times bar{B} d V(2)$$
где $bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I cdot B cdot d l cdot sin alpha(3)$$
где $alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Таблица перевода Ампер – Ватт
Для перевода ватт в амперы необходимо воспользоваться предыдущей формулой, развернув её. Чтобы вычислить ток, необходимо разделить мощность на напряжение: I = P/U. В следующей таблице представлена сила тока для приборов с различным напряжением — 6, 12, 24, 220 и 380 вольт.
Помните, что для сетей с высоким напряжением, указанная сила тока отличается в зависимости от коэффициента полезного действия.
Таблица соотношения ампер и ватт, в зависимости от напряжения.
| 24В | 220В | 380В | |||
| 5 Вт | 0,83А | 0,42А | 0,21А | 0,02А | 0,008А |
| 6 Вт | 1,00А | 0,5А | 0,25А | 0,03А | 0,009А |
| 7 Вт | 1,17А | 0,58А | 0,29А | 0,03А | 0,01А |
| 8 Вт | 1,33А | 0,66А | 0,33А | 0,04А | 0,01А |
| 9 Вт | 1,5А | 0,75А | 0,38А | 0,04А | 0,01А |
| 10 Вт | 1,66А | 0,84А | 0,42А | 0,05А | 0,015А |
| 20 Вт | 3,34А | 1,68А | 0,83А | 0,09А | 0,03А |
| 30 Вт | 5,00А | 2,5А | 1,25А | 0,14А | 0,045А |
| 40 Вт | 6,67А | 3,33А | 1,67А | 0,13А | 0,06А |
| 50 Вт | 8,33А | 4,17А | 2,03А | 0,23А | 0,076А |
| 60 Вт | 10,00А | 5,00А | 2,50А | 0,27А | 0,09А |
| 70 Вт | 11,67А | 5,83А | 2,92А | 0,32А | 0,1А |
| 80 Вт | 13,33А | 6,67А | 3,33А | 0,36А | 0,12А |
| 90 Вт | 15,00А | 7,50А | 3,75А | 0,41А | 0,14А |
| 100 Вт | 16,67А | 3,33А | 4,17А | 0,45А | 0,15А |
| 200 Вт | 33,33А | 16,66А | 8,33А | 0,91А | 0,3А |
| 300 Вт | 50,00А | 25,00А | 12,50А | 1,36А | 0,46А |
| 400 Вт | 66,66А | 33,33А | 16,7А | 1,82А | 0,6А |
| 500 Вт | 83,34А | 41,67А | 20,83А | 2,27А | 0,76А |
| 600 Вт | 100,00А | 50,00А | 25,00А | 2,73А | 0,91А |
| 700 Вт | 116,67А | 58,34А | 29,17А | 3,18А | 1,06А |
| 800 Вт | 133,33А | 66,68А | 33,33А | 3,64А | 1,22А |
| 900 Вт | 150,00А | 75,00А | 37,50А | 4,09А | 1,37А |
| 1000 Вт | 166,67А | 83,33А | 41,67А | 4,55А | 1,52А |
Используя таблицу также легко определить мощность, если известны напряжение и сила тока. Это пригодится не только для расчёта потребляемой энергии, но и для выбора специальной техники, отвечающей за бесперебойную работу или предотвращающей перегрев.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$bar{F}_{A}=I int_{l} d bar{l} times bar{B}(4)$$
где $bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl. Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I, в однородном магнитном поле действует сила Ампера равная $bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $mu_{0}=4 pi cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная. Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются. Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$frac{F}{l}=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Какие характеристики определяют силу тока в 1 ампер
Формальное определение данной единицы – ампер – было введено в 1948 году по предложению МКМВ (Международного комитета мер и весов). Оно гласит, что ампер – это сила постоянного тока, который протекает по беспредельно тонким длинным параллельным проводникам, отстоящим друг от друга на 1 метр и находящимся в вакууме, вызывая взаимодействие между ними силой 2 × 10−7 ньютона на каждый участок длиной 1 метр.
На практике воспроизвести условия определения невозможно, проводники имеют как конечную длину, так и конкретное сечение. Обычно сила взаимодействия определяется между двумя катушками с большим количеством витков провода. Этот принцип до 1992 года лежал в основе определения эталона ампера на токовых весах. При этом измерялась сила или момент сил, действующих на помещенную в магнитное поле катушку с током. Сила электрического тока измеряется амперметром.
С 1992 года эталон ампера в РФ определяется косвенным путем с использованием закона Ома, благодаря чему погрешность значения уменьшилась на два порядка.
Силу электрического тока можно представить как скорость изменения заряда, т. е. 1 ампер – это такая сила тока, когда за каждую секунду через поперечник проводника проходит количество электричества, равное 1 кулону (6,241·10¹⁸ электронов).
Направление силы Ампера
У силы Ампера есть одна важная особенность. Ее направление зависит от ориентации проводника. Она направлена перпендикулярно плоскости, образованной векторами тока и магнитной индукции. Если магнитная индукция и ток направлены по одной прямой, то сила Ампера равна нулю. Максимальной сила Ампера будет в том случае, если магнитная индукция перпендикулярна направлению движения тока.
Для определения направление силы Ампера пользуются правилом левой руки:
Следовательно, в формуле модуля силы Ампера должен быть еще один член — угол между направлениями магнитной индукции и тока.
Ватты в киловатты
Считается, что 1 ватт соответствует мощности, необходимой для совершения работы (1 Джоуль) за 1 секунду.
Связь между мощностью (Р), напряжением (U) и силой тока (I) представляют в виде формулы:
Р = U ∙ I.
Зная напряжение в сети и мощность приёмника, по этой формуле определяют силу тока, выбирают сечение провода и номинал защитного оборудования линии питания.
В настоящее время, чтобы вычислить, сколько ватт в ампере или кВ перевести в В, не обязательно производить вычисления самому. Достаточно в поисковике набрать онлайн калькулятор, например, с вопросом о переводе ватт в амперы, и будет выдан адрес нужного сайта.
Для удобства вычислений и обозначений ученые ввели производные Вт:
- Дольные, меньше Вт, используют в медицинском оборудовании (например, милливатт, микроватт, нановатт);
- Кратные, больше Вт, применяют в бытовых электроприборах (киловатт), в области энергетики (например, мегаватт, гигаватт).
Перевод этих величин из одной в другую возможен с помощью онлайн конвертера.
Мощность электрических приборов выражается в ваттах и кВт. Для удобства расчетов возникает необходимость приведения величин к одной системе исчисления. К примеру, ватт нужно преобразовать в кВт. Сколько ватт в киловатте? «Кило» означает, что число кратно тысяче. Выходит, что в одном кВт одна тысяча Вт. Чтобы посчитать, сколько в ватте будет киловатт, нужно данное количество Вт разделить на 1000.
Пример, как перевести правильно Вт в кВт:
- 1600 W = 1,6 kW;
- 40 W = 0,04 kW;
- 0,7 W = 0,0007 kW.
Чтобы выяснить, сколько будет киловатт в Вт, выполняют обратное действие – значение в кВт умножают на 1000:
- 2,4 kW = 2400 W;
- 0,6 kW = 600 W;
- 11,8 kW = 11800 W.
Сила Ампера
Как показывает опыт, магнитное поле не действует на покоящиеся электрические заряды. Однако, если заряд движется, то со стороны магнитного поля на него начинает действовать сила Лоренца, направленная перпендикулярно плоскости, которая образованна векторами скорости заряда и магнитной индукции. Электрический ток — это движение заряженных частиц. Для тока единицей измерения в физике принят ампер. Если проводник с током находится в магнитном поле, то на носители заряда действуют силы Лоренца, которые сливаются в общую силу, действующую на весь проводник в целом. Такая сила называется силой Ампера. От чего она зависит?
Очевидно, что, во-первых, раз сила Ампера порождается магнитным полем, то она должна быть пропорциональна величине магнитной индукции.
Во-вторых, поскольку магнитное поле действует на заряды, то сила Ампера должна быть пропорциональна величине заряда, движущегося в проводнике.
В-третьих, поскольку магнитное поле действует на движущийся заряд, то сила Ампера должна зависеть от скорости движения заряда.
Две последних величины — заряд и скорость его движения — хорошо характеризует такая величина, как сила тока. Напомним, сила тока — это отношение заряда, проходящего по проводнику, ко времени прохождения.
Наконец, количество носителей заряда в проводнике зависит от длины проводника.
Таким образом, сила Ампера должна быть пропорциональна величине магнитной индукции, силе тока в проводнике и длине проводника.
Как рассчитать число ампер в сети
На практике применяют разные схемы вычислений. В частности, пользуются автоматизированными программами (калькуляторами). Такие инструменты предлагают бесплатно специализированные сайты в режиме онлайн. Ниже представлены формулы и примеры, которые помогут рассчитывать электрические параметры самостоятельно.
Как узнать ток, зная мощность и напряжение
Источник питания постоянного тока (аккумулятор) обеспечивает напряжение на выходе 12 Вольт. Известна мощность потребления – 2 Вт. Как рассчитать ампераж, показано на примере:
К сведению. Для удобства на практике применяют дробные и кратные величины. В данном примере – 167 мА (миллиампер).
Как узнать напряжение, зная силу тока
Выше показано, как посчитать амперы, зная мощность и напряжение. Эту же формулу используют для обратного действия. Если сила тока равна 200 мА, при мощности 2 Вт в точках измерения, прибор покажет следующее напряжение:
U = P/I = 2/0,2 = 10 V.
Как рассчитать мощность, зная силу тока и напряжение
Результат можно вычислить с помощью следующего примера:
P = I*U = 0,2 * 10 = 2 Вт.
В левой части рисунка приведена формула для расчета механической мощности:
- А – полезная работа в Джоулях;
- t – временной период, за который выполнена эта операция.
Как определить мощность цепи, имея тестер сопротивления
В реальных условиях существенное влияние оказывает электрическое сопротивление проводника. Выбрав соответствующий режим, можно узнать действительное значение с помощью мультитестера. Переключатель устанавливают в положение, которое соответствует определенному диапазону. Переходят от больших значений к малым до появления индикации на экране.
При R=20 Ом, зная силу тока I= 200 мА, мощность вычисляют по следующей формуле:
P = I2*R = 0,04*20 = 0,8 Вт.
При необходимости уточняют напряжение:
Зачем нужно рассчитывать ток
На большинстве электроприборов указывается мощность потребления. Это необходимо для того, чтобы правильно вести учет потребления электроэнергии. Но для всего остального значение мощности несет мало информации. Параметры автоматов защиты и плавких вставок, сечение электропроводки, требуют знать протекающий ток или, как говорят электрики, ампераж нагрузки.
Вам это будет интересно Миллиамперы в амперы
Простой пример: какой паяльник сильнее перегружает электропроводку, 42-х вольтовый на 80 Вт или 220-и вольтовый на 100 Вт? Логичный ответ, что более мощный, является неправильным. Ведь на самом деле, при включении второго паяльника в сети протекает ток около 0.5 А, а при включении первого — почти 2 А. Соответственно, для таких устройств требуется различная электропроводка и номинал защитных устройств. При одинаковой толщине проводов питания нагрев будет сильнее, при работе с низковольтным инструментом.
По этой же причине в линиях электропередач стремятся по максимуму повысить передаваемое напряжение. Поскольку мощность нагрузки остается одинаковой, при более высоком напряжении по проводам протекает меньший ток и поэтому:
- Снижаются потери;
- Уменьшается нагрев;
- Снижается сечение проводов и, как следствие, их масса и нагрузка на опоры линий электропередач.
Как правильно рассчитать амперы по мощности и напряжению
Для того, чтобы правильно произвести вычисления, все используемые величины должны быть одной размерности, то есть, если мощность выражается в ваттах, то напряжение должно быть выражено в вольтах, а ток — в амперах.
Если оперируют мощностью в киловатт, то, соответственно, напряжение должно быть в киловольтах, а ток в килоамперах.
Обратите внимание! Последний случай характерен только для мощной энергетики, а в быту обычно используют ватт, вольт и ампер.
Лучше обновить в памяти правила перевода кратных единиц:
- Кило — тысяча;
- Киловатт — тысяча ватт (1кВт = 1000 Вт);
- Киловольт — тысяча вольт (1кВ = 1000 В);
- Килоампер — тысяча ампер (1кА = 1000А);
- Милли — одна тысячная;
- милливатт — одна тысячная ватта (1мВт = 0.001Вт);
- милливольт — одна тысячная вольта (1мВ = 0.001В);
- миллиампер — одна тысячная ампера (1мА = 0.001А).
Сейчас большое количество бытовой техники потребляют мощность более киловатта, поэтому для правильных вычислений нужно данную величину перевести в ватт.
Например: На электрочайнике написано, что мощность потребления равна 1.8 кВт. Для того, чтобы рассчитать величину тока при подключении к бытовой сети 220 В, в формулу надо подставлять 1800 Вт. Тогда на выходе получается ток в амперах.
Как и любая другая сила, сила Ампера имеет возможность совершить работу. По определению механической работы:
(1)
- где
Рис. 1. Работа силы Ампера
Пусть в нашей системе проводник длиной , находящийся в однородном магнитном поле индукции
, по которому течёт ток
, движется под действием силы Ампера и перемещается на расстояние
(рис. 1). Тогда, при условии, что сила Ампера равна
, получим:
(2)
Пометим — площадь, «заметаемая» при движении проводника. Т.е. площадь, которую «прошёл» проводник во время движения. Тогда, в общем случае:
(3)
- где
Соотношение (3) указывает на работу сил Ампера. Однако, если использовать определение изменения потока магнитного поля:
Ф
(4)
получим:
Ф (5)
- где
Содержание:
- Определение и формула силы Ампера
- Закон Ампера
- Силы, действующие на проводники с током в магнитном поле
- Единицы измерения силы Ампера
- Примеры решения задач
Определение и формула силы Ампера
Определение
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения:
$bar{F}, bar{F}_A$ . Сила Ампера векторная величина. Ее направление определяет
правило левой руки: следует расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее.
Вытянутые четыре пальца указывали направление силы тока. В таком случае отогнутый на
Закон Ампера
Элементарная сила Ампера
($dbar{F}_A$) определена законом (или формулой) Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(1)$$
где I – сила тока,
$d bar{l}$ – малый элемент длины проводника – это вектор, равный
по модулю длине проводника, направленный в таком же направлении как вектор плотности тока,
$bar{B}$ – индукция магнитного поля, в которое помещен проводник с током.
Иначе эту формулу для силы Ампера записывают как:
$$d bar{F}_{A}=bar{j} times bar{B} d V(2)$$
где $bar{j}$ – вектор плотности тока, dV – элемент объема проводника.
Модуль силы Ампера находят в соответствии с выражением:
$$d F=I cdot B cdot d l cdot sin alpha(3)$$
где $alpha$ – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что
сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.
Силы, действующие на проводники с током в магнитном поле
Из закона Ампера следует, что на проводник с током, равным I, действует сила равная:
$$bar{F}_{A}=I int_{l} d bar{l} times bar{B}(4)$$
где $bar{B}$ магнитная индукция, рассматриваемая в пределах малого кусочка проводника dl.
Интегрирование в формуле (4) проводят по всей длине проводника (l). Из выражения (4) следует, что на замкнутый контур с током I,
в однородном магнитном поле действует сила Ампера равная $bar{F}_{A}=0(H)$
Сила Ампера, которая действует на элемент (dl) прямого проводника с током I1, помещённый в магнитное поле, которое
создает другой прямой проводник, параллельный первому с током I2, равна по модулю:
$$d F=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d} d l(5)$$
где d – расстояние между проводниками, $mu_{0}=4 pi cdot 10^{7}$ Гн/м(или Н/А2 ) – магнитная постоянная.
Проводники с токами одного направления притягиваются. Если направления токов в проводниках различны, то они отталкиваются.
Для рассмотренных выше параллельных проводников бесконечной длины сила Амперана единицу длины может быть вычислена по формуле:
$$frac{F}{l}=frac{mu_{0}}{2 pi} frac{I_{1} I_{2}}{d}$$
Формулу (6) в системе СИ применяют для получения количественного значения магнитной постоянной.
Единицы измерения силы Ампера
Основной единицей измерения силы Ампер (как и любой другой силы) в системе СИ является: [FA]=H
В СГС: [FA]=дин
Примеры решения задач
Пример
Задание. Прямой проводник длины l с током I находится в однородном магнитном поле B. На проводник
действует сила F. Каков угол между направлением течения тока и вектором магнитной индукции?
Решение. На проводник с током, находящийся в магнитном поле действует сила Ампера, модуль которой для
прямолинейного проводника с током расположенном в однородном поле можно представить как:
$$F=F_{A}=I B operatorname{lsin} alpha$$
где $alpha$ – искомый угол. Следовательно:
$$alpha=arcsin left(frac{F}{I B l}right)$$
Ответ. $alpha=arcsin left(frac{F}{I B l}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
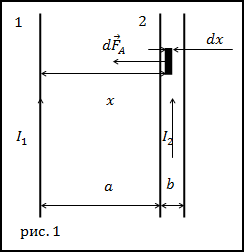
Задание. Два тонких, длинных проводника с токами лежат в одной плоскости на расстоянии d друг от друга.
Ширина правого проводника равна a. По проводникам текут токи I1 и I2 (рис.1). Какова, сила Ампера, действующая
на проводники в расчете на единицу длины?
Решение. За основу решения задачи примем формулу элементарной силы Ампера:
$$d bar{F}_{A}=I d bar{l} times bar{B}(2.1)$$
Будем считать, что проводник с током I1 создает магнитное поле, а другой проводник в нем находится.Станем искать силу
Ампера, действующую на проводник с током I2. Выделим в проводнике (2) маленький элемент dx (рис.1), который находится
на расстоянии x от первого проводника. Магнитное поле, которое создает проводник 1 (магнитное поле бесконечного прямолинейного проводника с
током) в точке нахождения элементаdxпо теореме о циркуляции можно найти как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Вектор магнитной индукции в точке нахождения элемента dx направлен перпендикулярно плоскости
рисунка, следовательно, модуль элементарной силы Ампера, действующий на него можно представить как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где ток, который течет в элементе проводника dx, выразим как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
Тогда выражение для dFA, учитывая (2.2) и (2.4) запишем как:
$$B cdot 2 pi x=mu_{0} I_{1} rightarrow B=frac{mu_{0} I_{1}}{2 pi x}$$
где из рис.1 видно, что $a leq x leq a+b$, по условию задачи силу следует
найти на единицу длины, значит $0 leq l leq 1$ . Для нахождения суммарной силы Ампера, действующей на проводник (2) возьмем двойной интеграл от выражения (2.5):
$$F_{A}=int_{a}^{a+b} int_{0}^{1} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x d l=int_{a}^{a+b} frac{mu_{0} I_{1}}{2 pi x} cdot frac{I_{2}}{b} d x=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$$
Проводники действуют друг на друга с силами равными по модулю и так как токи направлены одинаково, то они притягиваются.
Ответ. $F_{A}=frac{mu_{0} I_{1}}{2 pi} cdot frac{I_{2}}{b} ln left|frac{a+b}{a}right|$
Читать дальше: Формула силы выталкивания.