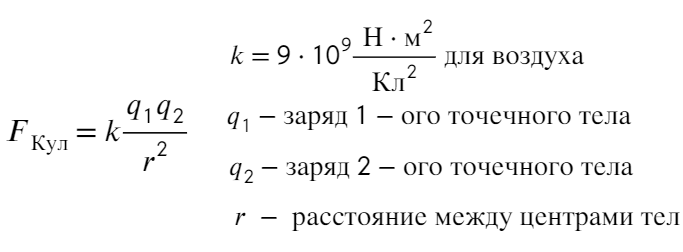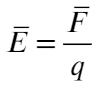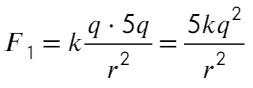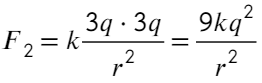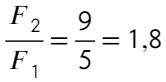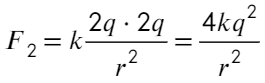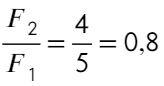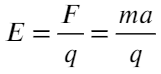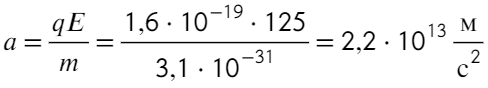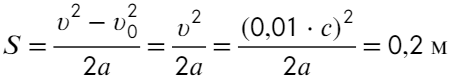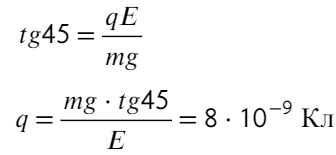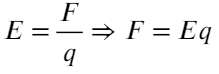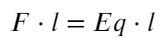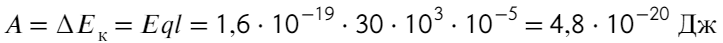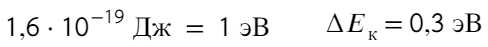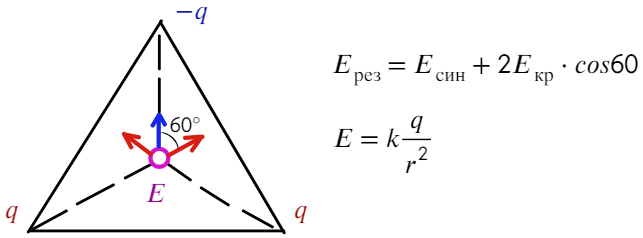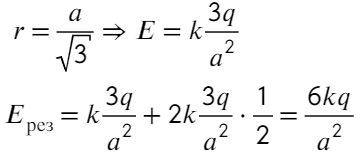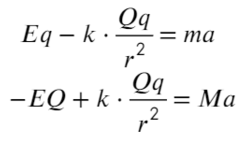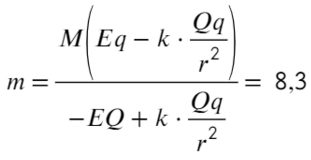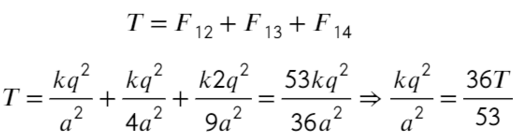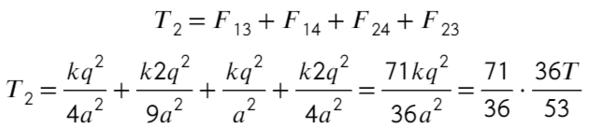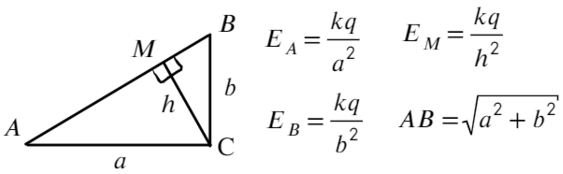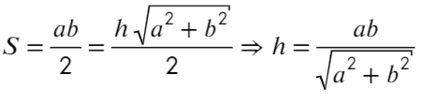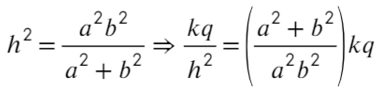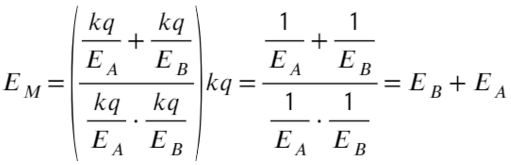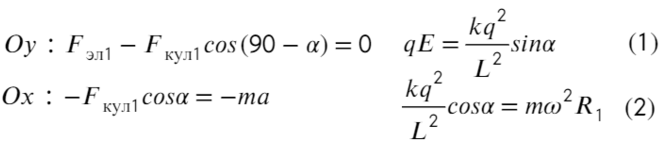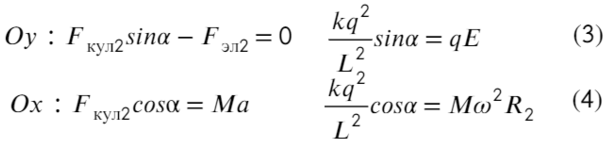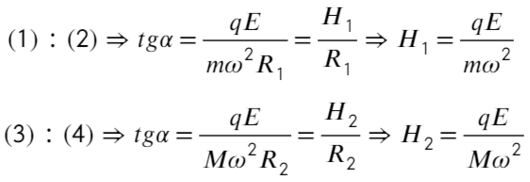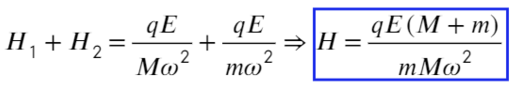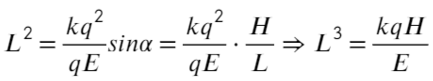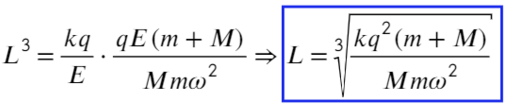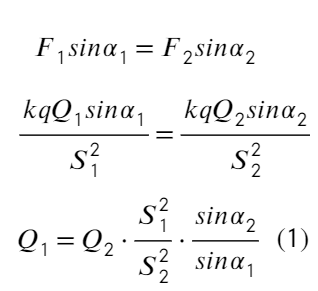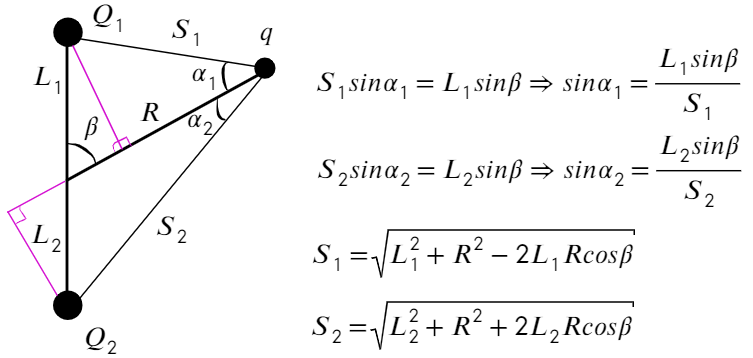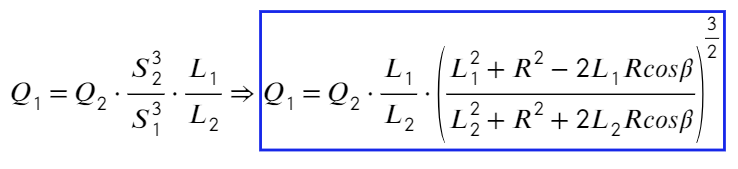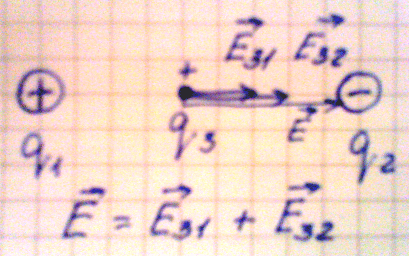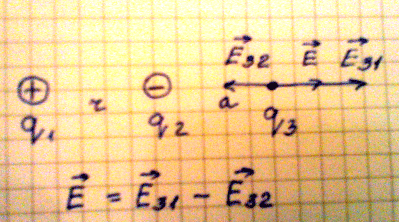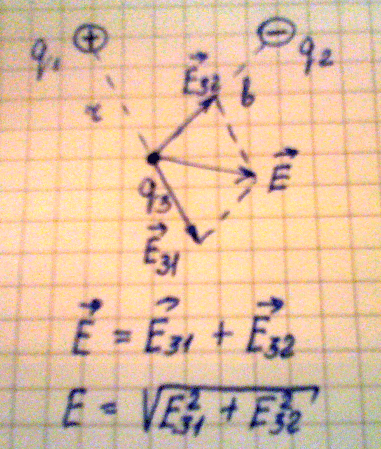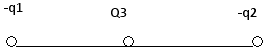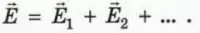Как найти модуль напряженности разноименного заряда - Avtoru.top

Закон Кулона

Закон сохранения электрического заряда

Напряженность

Принцип суперпозиции

Электрическое поле

Потенциал электростатического поля

Разность потенциалов

Теория

Совсем чуть−чуть.

Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.

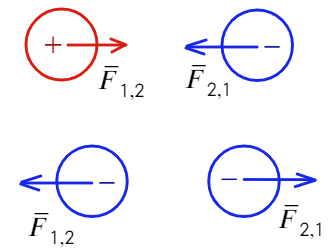
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:

Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.

Напряженность НЕ зависит от величины заряда, помещенного в поле!

Задачи

Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.

Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:

А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:

Отношение получится таким:

Ответ: 1,8

Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.

Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).

А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:

Отношение:

Ответ: 0,8

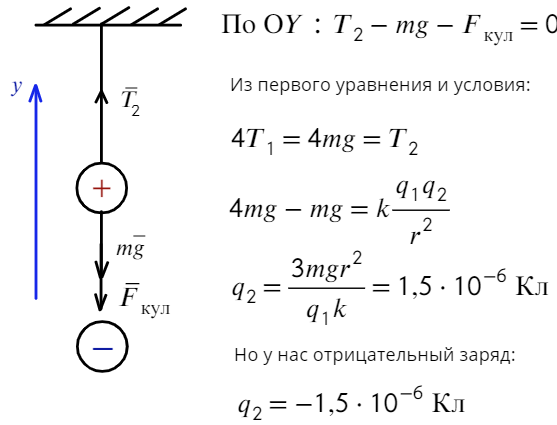
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?

В начальный момент времени на шарик действуют две силы:

а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:

б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:

Ответ: −1,5 мкКл, 500 нКл.

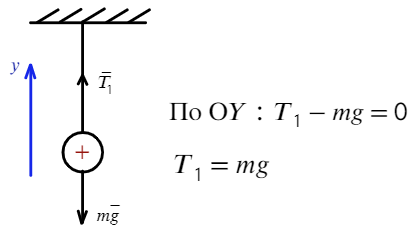
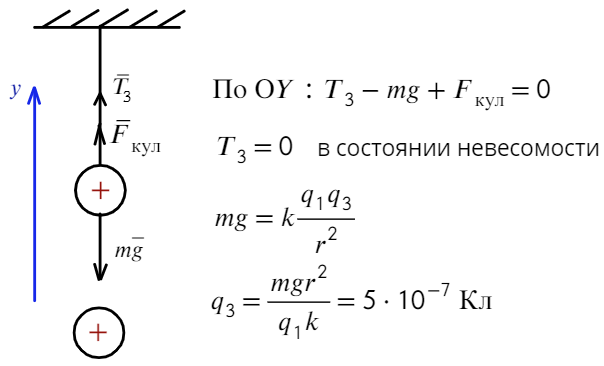
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.

В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.

Найдем ускорение электрона в электрическом поле:

Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:

Ответ: 0,2 м

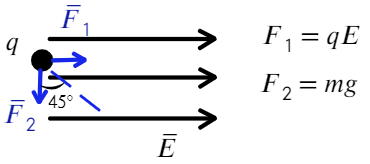
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?

Для начала разберемся, какие силы действуют на заряд:

Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:

Ответ: 8×10⁻⁹ Кл

Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)

Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:

Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:

Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹

Ответ: 0,3 эВ

Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.

Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).

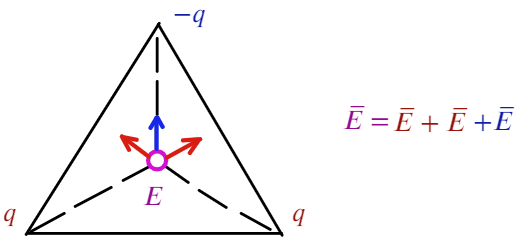
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:

Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:

Ответ: 6kq/a²

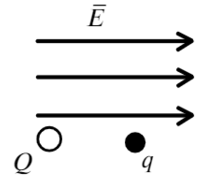
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ — 2016)

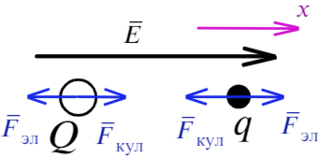
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.

На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:

Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.

Разделим одно уравнение на другое и выразим массу:

Ответ: 8,3 гр.

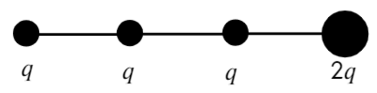
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)

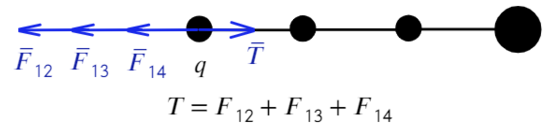
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:

Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.

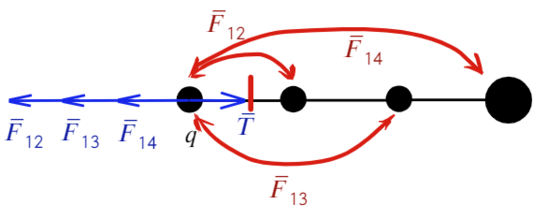
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:

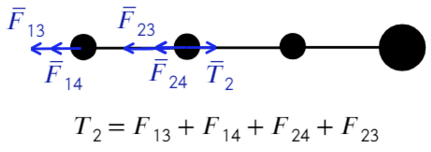
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:

Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:

Второе уравнение с подстановкой выражения из первого:

Ответ: 71T/53

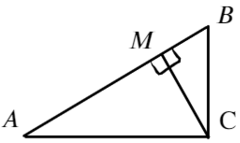
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)

Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:

Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:

Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:

Выразим a² и b² через напряженность:

Ответ: Ea+Eb

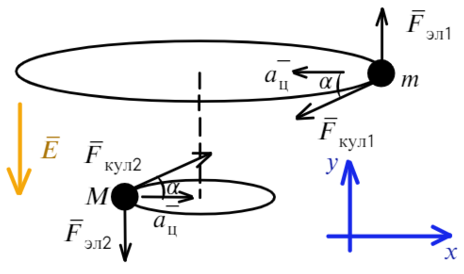
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)

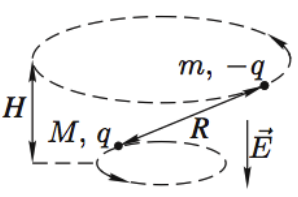
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:

Запишем уравнения по осям на верхнюю частицу:

На нижнюю частицу:

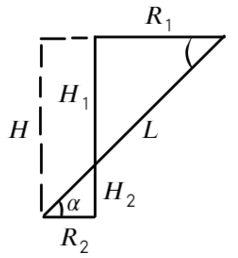
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.

Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:

Сложим два уравнения, чтобы найти расстояние между плоскостями:

Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:

Вместо Н подставим то, что мы нашли:

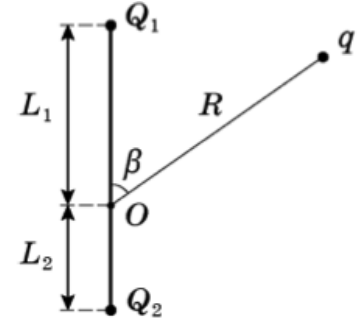
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)

Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:

Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:

Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:

Подставим в ур-ие (1):

В качестве закрепления материала решите несколько похожих задач с ответами.

Будь в курсе новых статеек, видео и легкого технического юмора.

Источник

Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.

Задачи урока:

формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля;
научить учащихся применять формулу E=kq/r² в решении
несложных задач на расчёт напряжённости.

Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.

Графически изображая поле, следует помнить, что линии напряженности
электрического поля:

нигде не пересекаются друг с другом;
имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями;
между зарядами нигде не прерываются.

Рис.1

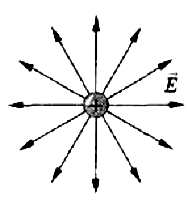
Силовые линии положительного заряда:

Рис.2

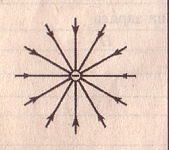
Силовые линии отрицательного заряда:

Рис.3

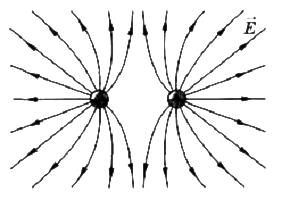
Силовые линии одноименных взаимодействующих зарядов:

Рис.4

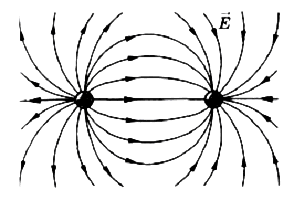
Силовые линии разноименных взаимодействующих зарядов:

Рис.5

Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда

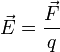
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда

где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.

В системе СИ
Н·м²/Кл²,

где ε₀ – электрическая
постоянная, равная 8,85·10^-12 Кл²/Н·м²;

q – электрический заряд (Кл);

r – расстояние от заряда до точки в которой определяется напряженность.

Направление вектора напряженности совпадает с направлением силы Кулона.

Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.

Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:

Рассмотрим несколько случаев определения напряженности.

1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:

Е₃₁ – напряженность точечного заряда 3 со стороны заряда 1;

Е₃₂ – напряженность точечного заряда 3 со стороны заряда 2.

Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е₃₁ и Е₃₂.

Напряженность в данной точке определяется по формуле:

Е = kq₁/x² + kq₂/(r – x)²

где: r – расстояние между первым и вторым зарядом;

х – расстояние между первым и точечным зарядом.

Рис.6

2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е₃₁и Е₃₂.

Формула напряженности в данной точке равна:

Е = kq1/(r + a)² – kq₂/a²

Где: r – расстояние между взаимодействующими зарядами;

а – расстояние между вторым и точечным зарядом.

Рис.7

3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:

Е = (Е₃₁² +Е₃₂²)^1/2

Следовательно:

Е = ((kq₁/r² )² + (kq₂/b²)²)^1/2

Рис.8

Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.

4. Закрепление темы.

Проверочная работа.

Вариант № 1.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: электрическое поле – это ….

3. Как направлены силовые линии напряженности данного заряда?

4. Определить знаки зарядов:

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Вариант № 2.

1. Продолжить фразу: “электростатика – это …

2. Продолжить фразу: напряженностью называется …

3. Как направлены силовые линии напряженности данного заряда?

4. Определить заряды.

5. Указать вектор напряженности.

6. Определить напряженность в точке В исходя из суперпозиции полей.

Своя оценка работы	Оценка работы другим учеником

Задачи на дом:

1. Два заряда q₁ = +3·10^-7 Кл и q₂ = −2·10^-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q₂.

2. В некоторой точке поля на заряд 5·10^-9 Кл действует сила 3·10^-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.

Источник

Задача. Электростатическое поле создано находящимися на расстоянии $displaystyle left| {{q}_{1}} right|=left| {{q}_{2}} right|=3,8$ см друг от друга двумя разноимёнными зарядами, модули которых $displaystyle left| {{q}_{1}} right|=left| {{q}_{2}} right|=3,8$ нКл. Определите модуль напряжённости и потенциал в средней точке отрезка, соединяющего эти заряды.

Дано:

displaystyle r=60 см
$displaystyle left| {{q}_{1}} right|=left| {{q}_{2}} right|=3,8$ нКл

Найти:
$displaystyle {{varphi }_{0}}$ — ?
$displaystyle {{E}_{0}}$ — 7

Решение

Думаем: источником электростатического поля в задаче являются точечные заряды, тогда:

для модуля напряжённости точечного заряда:

$displaystyle E=kfrac{q}{{{r}^{2}}}$ (1)

для потенциала точечного заряда:

$displaystyle varphi =kfrac{q}{r}$ (2)

Т.к. зарядов несколько,, то для поиска общих параметров системы будем использовать принцип суперпозиции:

для вектора напряжённости (вектор полной напряжённости равен векторной сумме напряжённостей, создаваемых каждым из зарядов):

$displaystyle {{vec{E}}_{0}}=sumlimits_{i}{{{{vec{E}}}_{i}}}$ (3)

для потенциала (полный потенциал, создаваемый в точке равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в этой точке):

$displaystyle {{varphi }_{0}}=sumlimits_{i}{varphi {}_{i}}$ (4)

Решаем: для (1) и (2) нам необходимо визуализировать систему (рис. 1).

Рис. 1. Система зарядов в задаче

Расставим напряжённости, создаваемые в исходной точке от двух зарядов-источников (рис. 2). Помним, что от положительного заряда линии напряжённости «уходят», к отрицательному «приходят». Для определённости будем считать, что $displaystyle {{q}_{2}}<0$ , а $displaystyle {{q}_{2}}<0$ .

Рис. 2. Напряжённость, создаваемая зарядами

Тогда, исходя из (3):

$displaystyle {{vec{E}}_{0}}={{vec{E}}_{1}}+{{vec{E}}_{2}}$ (5)

В проекции на ось ОХ:

$displaystyle {{E}_{0}}={{E}_{1}}+{{E}_{2}}$ (6)

Значение напряжённости от каждого из зарядов можно найти исходя из (1):

$displaystyle {{E}_{1}}=kfrac{left| {{q}_{1}} right|}{{}^{r}!!diagup!!{}_{2};}=kfrac{2left| {{q}_{1}} right|}{r}$ (7)

$displaystyle {{E}_{2}}=kfrac{left| {{q}_{2}} right|}{{}^{r}!!diagup!!{}_{2};}=kfrac{2left| {{q}_{2}} right|}{r}$ (8)

Подставим в (6):

$displaystyle {{E}_{0}}=kfrac{2left| {{q}_{1}} right|}{r}+kfrac{2left| {{q}_{2}} right|}{r}=frac{2k}{r}(left| {{q}_{1}} right|+left| {{q}_{2}} right|)$ (9)

Для потенциала всё ещё проще. Воспользуемся (4):

$displaystyle {{varphi }_{0}}=left| {{varphi }_{1}}+{{varphi }_{2}} right|$ (10)

Значение потенциала, создаваемого каждым зарядом найдём из (2):

$displaystyle {{varphi }_{1}}=kfrac{{{q}_{1}}}{{}^{r}!!diagup!!{}_{2};}=kfrac{2{{q}_{1}}}{r}$ (11)

$displaystyle {{varphi }_{2}}=kfrac{{{q}_{2}}}{{}^{r}!!diagup!!{}_{2};}=kfrac{2{{q}_{2}}}{r}$ (12)

Подставим (11) и (12) в (10):

$displaystyle {{varphi }_{0}}=left| kfrac{2{{q}_{1}}}{r}+kfrac{2{{q}_{2}}}{r} right|=frac{2k}{r}left| {{q}_{1}}+{{q}_{2}} right|$ (13)

Для потенциала главное использовать заряд со своим знаком.

Считаем: вспоминаем константы $displaystyle ^{2}$ Н*м $displaystyle ^{2}$ /Кл $displaystyle ^{2}$ , И не забываем перевести все параметры (расстояния) в единицы СИ.

$displaystyle {{E}_{0}}=frac{2*9*{{10}^{9}}}{{{(0,60)}^{2}}}(3,8*{{10}^{-9}}+3,8*{{10}^{-9}})=3,8*{{10}^{-7}}$ Н/м

$displaystyle {{varphi }_{0}}=frac{2*9*{{10}^{9}}}{0,60}left| 3,8*{{10}^{-9}}-3,8*{{10}^{-9}} right|=0$ В

Ответ: $displaystyle {{varphi }_{0}}=0$ Н/м; $displaystyle {{varphi }_{0}}=0$ В.

Ещё задачи на тему «Потенциал электростатического поля»

Источник

1. Определение напряженности

Как вы уже знаете из курса физики основной школы, электрическое взаимодействие заряженных тел осуществляется посредством электрического поля: каждое заряженное тело создает вокруг себя электрическое поле, которое действует на другие заряженные тела. Представление об электрическом поле ввел английский ученый Майкл Фарадей в первой половине 19-го века.

Электрическое поле в данной точке пространства можно охарактеризовать с помощью силы, действующей со стороны этого поля на точечный заряд, помещенный в данную точку. (Этот заряд должен быть достаточно мал, чтобы создаваемое им поле не изменяло распределения зарядов, которые создают данное поле.)

Как показывает опыт, сила 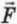, действующая на заряд q, пропорциональна величине этого заряда. Следовательно, отношение силы к заряду не зависит от величины заряда и характеризует само электрическое поле.

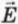
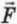
Напряженностью электрического поля в данной точке называют физическую величину, равную отношению силы , действующей со стороны поля на заряд q, помещенный в данную точку поля, к величине этого заряда:

Напряженность поля – векторная величина. Ее направление в каждой точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.

Единицей напряженности поля является 1 Н/Кл. 1 Н/Кл – небольшая напряженность. Например, напряженность электрического поля вблизи поверхности Земли, обусловленная электрическим зарядом Земли, составляет примерно 130 Н/Кл.

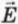
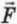
Если известна напряженность поля в данной точке, то можно найти силу , действующую на заряд q, помещенный в эту точку, по формуле

Из формул (1) и (2) следует, что направление напряженности поля в данной точке совпадает с направлением силы, действующей на положительный заряд, помещенный в эту точку.

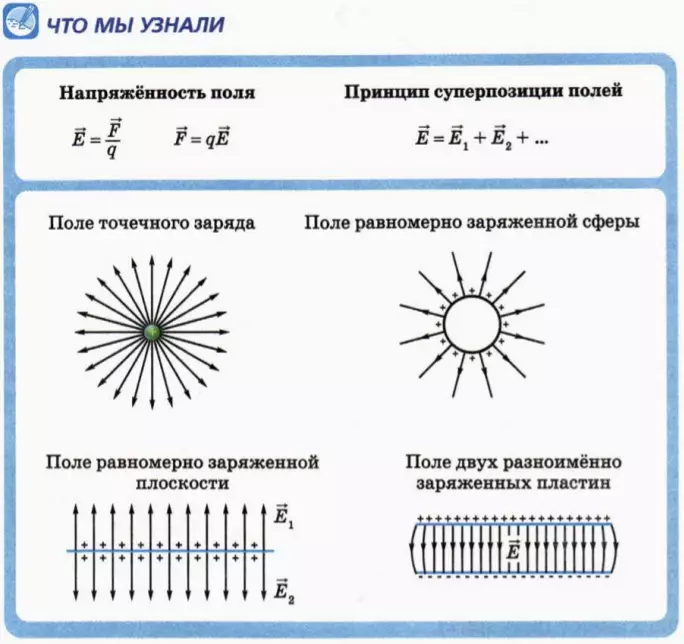
Напряженность поля точечного заряда

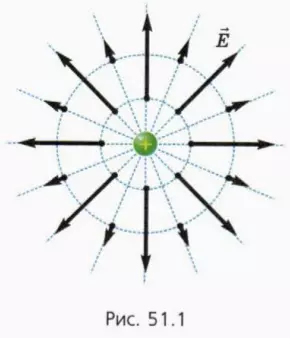
Если внести в поле положительного точечного заряда Q другой положительный заряд, он будет отталкиваться от заряда Q.

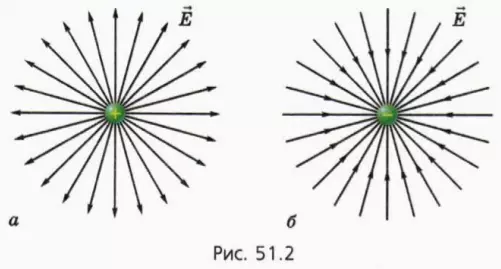
Следовательно, напряженность поля положительного точечного заряда во всех точках пространства направлена от этого заряда. На рисунке 51.1 изображены векторы напряженности поля точечного заряда в некоторых точках. Видно, что при удалении от заряда модуль напряженности поля уменьшается.

? 1. Объясните, почему модуль напряженности поля точечного заряда Q на расстоянии r от заряда выражается формулой

Подсказка. Воспользуйтесь законом Кулона и определением напряженности поля.

? 2. Чему равна напряженность поля точечного заряда 2 нКл на расстоянии 2 м от него?

? 3. Модуль напряженности поля точечного заряда на расстоянии 0,5 м от него равен 90 Н/Кл. Чему может быть равен этот заряд?

Принцип суперпозиции полей

Если заряд находится в поле, созданном несколькими зарядами, то каждый из этих зарядов действует на данный заряд независимо от других.

Отсюда следует, что равнодействующая сил, действующих на данный заряд со стороны других зарядов, равна векторной сумме сил, действующих на данный заряд со стороны каждого из остальных зарядов.

Это означает, что справедлив принцип суперпозиции полей:

напряженность поля, созданного несколькими зарядами, равна векторной сумме напряженностей полей, созданных каждым из зарядов:

Используя принцип суперпозиции, можно найти напряженность поля, создаваемого несколькими зарядами.

? 4. Два точечных заряда расположены на расстоянии 60 см друг от друга. Модуль каждого заряда равен 8 нКл. Чему равен модуль напряженности поля, создаваемого этими зарядами:
а) в точке, расположенной на середине отрезка, соединяющего заряды, если заряды одноименные? разноименные?
б) в точке, находящейся на расстоянии 60 см от каждого заряда, если заряды одноименные? разноименные?

Для каждого из этих случаев сделайте в тетради чертеж, поясняющий решение.

2. Линии напряженности

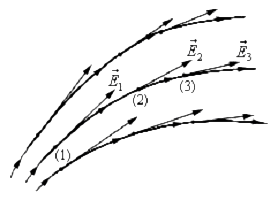
На примере поля точечного заряда (рис. 51.1) можно заметить, что векторы напряженности электрического поля в разных точках пространства выстраиваются вдоль некоторых линий.

В случае точечного заряда эти линии представляют собой прямые лучи, проведенные из точки, в которой находится заряд. В поле, созданном несколькими зарядами, зти линии будут некоторыми кривыми, причем напряженность поля в каждой точке будет направлена по касательной к одной из таких линий.

Воображаемые линии, касательные к которым в каждой точке совпадают с направлением напряженности электрического поля, называют линиями напряженности электрического поля.

Линии напряженности начинаются на положительных зарядах и заканчиваются на отрицательных. Густота линий напряженности пропорциональна модулю напряженности.

? 5. Объясните, почему линии напряженности электрического поля не могут пересекаться.

Поля точечных зарядов

? 6. Объясните, почему линии напряженности электрического поля положительного и отрицательного точечных зарядов имеют вид, изображенный на рисунках 51.2, а и 51.2, б.

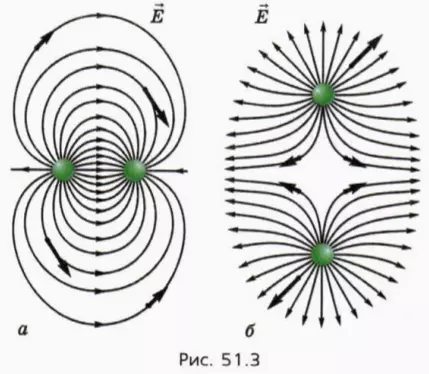
? 7. На рисунке 51.3 изображены линии напряженности поля, созданного одинаковыми по модулю зарядами (разноименными и одноименными). В некоторых точках для наглядности изображены векторы напряженности поля.

а) Перенесите рисунки в тетрадь и обозначьте на них знаки зарядов.
б) Изобразите в тетради линии напряженности поля, созданного двумя одноименными зарядами, которое не совпадает ни с одним из приведенных рисунков.
в) Чему равна напряженность поля в центральной точке рисунка 51.3, б (в середине отрезка, соединяющего заряды? Поясните ваш ответ с помощью закона Кулона.

Поле равномерно заряженной сферы

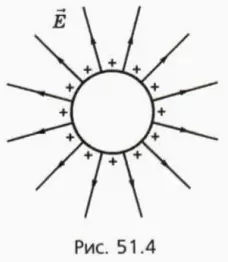
На рисунке 51.4 изображены линии напряженности электрического поля равномерно заряженной сферы.

Мы видим, что вне сферы зто поле совпадает с полем точечного заряда, ровного суммарному заряду сферы и расположенного в центре сферы.
Можно доказать, что внутри заряженной сферы напряженность поля ровна нулю. (Доказательство этого факта выходит за рамки нашего круга.)

? 8. На сфере радиусом 5 см находится заряд 6 нКл. Чему равна напряженность поля этого заряда:
а) в центре сферы?
б) на расстоянии 4 см от центра сферы?
в) на расстоянии 10 см от центра сферы?
г) вне сферы на расстоянии 1 см от ближайшей к этой точке поверхности сферы?

Однако напряженность электрического поля внутри заряженной сферы не обязательно равна нулю! Если внутри этой сферы находится заряженное тело, то согласно принципу суперпозиции напряженность электрического поля равна векторной сумме напряженности поля, создаваемого зарядом этого тела, и напряженности поля, создаваемого зарядом сферы.

Внутри сферы поле создается только заряженным телом, находящимся внутри сферы, потому что напряженность поля, созданного заряженной сферой, внутри сферы равна нулю. А в любой точке вне сферы напряженность поля можно найти, складывая векторы напряженности поля, создаваемого телом, расположенным внутри сферы, и поля, создаваемого зарядом сферы.

? 9. Имеются две концентрические (имеющие общий центр) сферы радиусом 5 см и 10 см. Заряд внутренней сферы равен 6 нКл, а заряд внешней сферы равен –9 нКл. Чему равен модуль напряженности поля в точке, находящейся от общего центра сфер на расстоянии, равном:
а) 3 см; б) 6 см; в) 8 см; г) 12 см; д) 20 см?

Поле равномерно заряженной плоскости

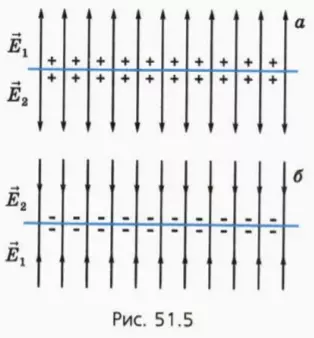
На рисунке 51.5 изображены линии напряженности электрического поля вблизи равномерно заряженной плоской пластины.

Будем считать, что размеры пластины намного больше расстояний от нее до тех точек пространства, в которых мы рассматриваем напряженность поля. В таких случаях говорят о поле равномерно заряженной плоскости.

Напряженность поля равномерно заряженной плоскости практически одинакова (по модулю и по направлению) во всех точках пространства по одну сторону от плоскости. Линии напряженности этого поля представляют собой параллельные прямые, перпендикулярные плоскости и расположенные на равных расстояниях друг от друга. Такое электрическое поле называют однородным.

По другую сторону плоскости изменяется только направление напряженности поля, а ее модуль остается таким же.

? 10. Напряженность электрического поля, создаваемого большой однородно заряженной пластиной, равна 900 Н/Кл. На расстоянии 40 см от пластины находится точечный заряд, равный по модулю 1 нКл.
а) На каком расстоянии от точечного заряда модуль напряженности его поля равен модулю напряженности поля пластины?
б) На каком расстоянии от плоскости результирующая напряженность поля плоскости и точечного заряда равна нулю, если знак точечного заряда совпадает со знаком заряда плоскости? Если знак точечного заряда противоположен знаку заряда плоскости?

Поле двух разноименно заряженных плоских пластин

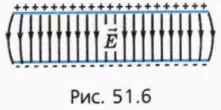
Возьмем две одинаковые равномерно заряженные пластины, заряды которых равны по модулю, но противоположны по знаку. Расположим пластины параллельно друг друту на малом расстоянии друг от друга (рис. 51.6).

? 11. Объясните, почему в пространстве между пластинами напряженность поля в 2 раза больше, чем напряженность поля, создаваемого каждой из пластин, а вне пластин практически равна нулю.
Подсказка. Воспользуйтесь принципом суперпозиции электрических полей.

Как увидеть линии напряженности?

Поставим опыт
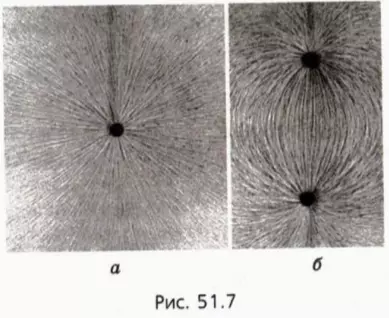
Поместим в электрическое поле состоящие из диэлектрика мелкие тела продолговатой формы – кристаллики, частицы манной крупы, мелко настриженные волосы и т. п. В электрическом поле они поворачиваются так, чтобы их более длинная сторона была направлена вдоль вектора напряженности поля. В результате эти тела выстраиваются вдоль линий напряженности, делая их форму видимой. На рисунке 51.7 приведены полученные таким образом «картины» электрических полей, создаваемых заряженным шариком (рис. 51.7, а) и двумя разноименно заряженными шариками (рис. 51.7, б).

Дополнительные вопросы и задания

12. Небольшой заряженный шарик массой 0,2 г подвешен на нити в однородном электрическом поле, напряженность которого направлена горизонтально и равна по модулю 50 кН/Кл.
а) Изобразите на чертеже положение равновесия шарика и силы, действующие на него.
б) Чему равен заряд шарика, если нить отклонена от вертикали на угол 30º?

13. Какова должна быть напряженность поля, чтобы капелька воды радиусом 0,01 мм находилась в этом поле в равновесии, потеряв 10³ электронов? Как должна быть направлена напряженность поля?

Источник

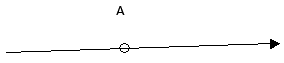
Где в системе из двух разноименных зарядов напряженность равна 0?

Напряженность — величина векторная, поэтому сумма векторов должна быть равна нулю. Из этого следует, что векторы должны быть направлены встречно, а их модули равны. Тогда очевидно, что если заряды одноименны, такая точка, где напряженность равна нулю, находится на оси между зарядами. Если заряды разноименные (разные по знаку) такая точка находится на продолжении оси, соединяющей заряды, как показано на рисунке выше. Конкретное местоположение этой точки зависит от величины каждого из зарядов и вот почему. Модуль вектора напряженности определяется по формуле:

$E=frac{q}{4pivarepsilon_0varepsilon R^2}$

Тогда, исходя из изложенного принципа, что модули напряженности, создаваемой каждым из зарядов, равны, можем записать:

$frac{q_1}{4pivarepsilon_0varepsilon R_1^2}=frac{q_2}{4pivarepsilon_0varepsilon R_2^2}$ $ (1)

Обозначим расстояние между зарядами L, тогда расстояние искомой точки х, от второго заряда:

$R_2=L-R_1$ (2)

Подставим (2) в (1):

$frac{q_1}{R_1^2}=frac{q_2}{(L-R_1)^2}$ (3)

Решаем квадратное уравнение (3) и получаем:

$R_1=2q_1Lpmsqrt{frac{4q_1^2L^2-4(q_1-q_2)q_1L^2}{2(q_1-q_2)}}$

Ну, а если заряды разного знака, то (2) надо записать соответственно и далее алгоритм тот же.

Источник

Теория

Задачи

1. Определение напряженности

Напряженность поля точечного заряда

Принцип суперпозиции полей

2. Линии напряженности

Поля точечных зарядов

Поле равномерно заряженной сферы

Поле равномерно заряженной плоскости

Поле двух разноименно заряженных плоских пластин

Как увидеть линии напряженности?

Дополнительные вопросы и задания

Где в системе из двух разноименных зарядов напряженность равна 0?

Не пропустите также: