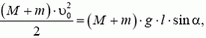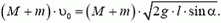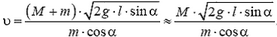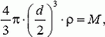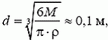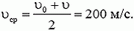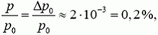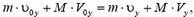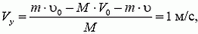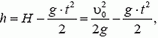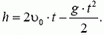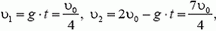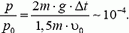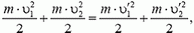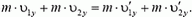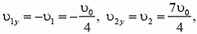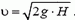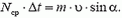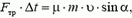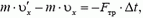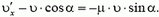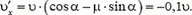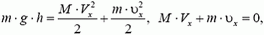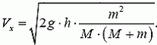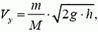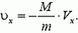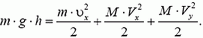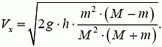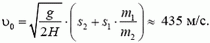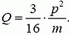Как найти модуль импульса до столкновения - Avtoru.top

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p₀ – p = m(v₀ – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p = 2mv₀
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁+ m₂)v

Отсюда скорость равна:

Задание EF17556

Импульс частицы до столкновения равен −p₁, а после столкновения равен −p₂, причём p₁= p, p₂= 2p, −p₁⊥−p₂. Изменение импульса частицы при столкновении Δ−p равняется по модулю:

а) p

б) p√3

в) 3p

г) p√5

Алгоритм решения

1.Записать исходные данные.

2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.

3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.

4.Подставить известные значения и вычислить.

Решение

Запишем исходные данные:

• Модуль импульса частицы до столкновения равен: p₁= p.

• Модуль импульса частицы после столкновения равен: p₂= 2p.

• Угол между вектором начального и вектором конечного импульса: α = 90^о.

Построим чертеж:

Так как угол α = 90^о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δp=√p21+p22

Подставим известные данные:

Δp=√p2+(2p)2=√5p2=p√5

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17695

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Алгоритм решения

1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.

2.Сделать вывод о том, как зависит характер движения от импульса.

3.На основании вывода и анализа графика установить характер движения тела на интервалах.

Решение

Импульс тела есть произведение массы тела на его скорость:

p = mv

Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.

На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.

Верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22730

Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.

Алгоритм решения

1.Записать исходные данные.

2.Записать закон сохранения импульса применительно к задаче.

3.Записать формулу кинетической энергии тела.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса камня: m₁ = 3 кг.

• Масса тележки с песком: m₂ = 15 кг.

• Кинетическая энергия тележки с камнем: E_k = 2,25 Дж.

Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:

m1v1+m2v2=(m1+m2)v

Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:

m1v1cosα=(m1+m2)v

Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:

Ek=(m1+m2)v22

Отсюда скорость равна:

v=√2Ekm1+m2

Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:

v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2

Подставим известные данные и произведем вычисления:

v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)

Ответ: 6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22520

Снаряд, имеющий в точке О траектории импульсp₀, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:

а) −−→AB

б) −−→BC

в) −−→CO

г) −−→OD

Алгоритм решения

1.Сформулировать закон сохранения импульса и записать его в векторной форме.

2.Применить закон сохранения импульса к задаче.

3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:

−p1+−p2=−p′
1+−p′2

Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:

−p0=−p1+−p2

Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:

−p2=−p0−−p1

Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18122

Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?

Ответ:

а) 27 г

б) 64 г

в) 81 г

г) 100 г

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.

3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса пластилиновой пули: m = 9 г.

• Скорость пластилиновой пули: v = 20 м/с.

• Максимальный угол отклонения нити: α = 60°.

Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.

После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:

mv=(m+M)V

После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.

Закон сохранения энергии для точки В:

(m+M)V22=(m+M)gh

V22=gh

Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:

V=√2glcosα

Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 20.2k

Источник

В статье рассказывается о том, как рассчитать импульс до столкновения, с его формулами и проблемами.

Импульс перед столкновением оценивается как несущий произведение массы и скорости. Перед столкновением нет внешней силы, изменяющей движение. Итак, объект, имеющий массу в состоянии покоя, считается имеющим нулевой импульс, или объект представляет собой движение, которое считается движущимся с импульсом.

Импульс объекта до столкновения равен P = mv.

В отсутствие внешняя сила, его движение и импульс не меняются до столкновения.

Узнать больше о Momentum.

Каков импульс автомобиля массой 60 кг, движущегося со скоростью 120 км/ч до столкновения с другими транспортными средствами?

Как рассчитать импульс перед столкновением

Данный:

m = 60 кг

v = 120 км / ч

v = 120 х 1000/3600 м/с

Найти: П =?

Формула:

Р = мв

Решения:

Импульс автомобиля перед столкновением рассчитывается как,

Р = мв

Подставляем все значения

Р = 60 х 120 х 1000/3600

Р = 7200000/3600

Р = 2000

Импульс автомобиля перед столкновением равен 2000 кг.м/с.

Столкновение из-за большого импульса
Двигайтесь с низким импульсом. Безопасное вождение
(Кредит: Shutterstock)

Как найти общий импульс двух тел перед столкновением?

Суммарный импульс двух объектов перед столкновением рассчитывается с использованием закона сохранения импульса.

При столкновении двух объектов с разными массами и скоростями их индивидуальный импульс может измениться. Тем не менее, их общий импульс остается неизменным в соответствии с законом сохранения импульса. Итак, перед столкновением мы вычисляем импульс двух объектов, складывая их индивидуальный импульс.

Компания сохранение импульса говорит:

P_{перед столкновением}= P_{после столкновения}

m₁u₁ + м₂u₂ = м₁v₁ + м₂v₂

Где м₁u₁ — импульс 1-го объекта, а m₂u₂ — импульс 2-го объекта до столкновения.

Где м₁v₁ — импульс 1-го объекта, а m₂v₂— импульс второго объекта после столкновения.

Когда мы хотим вычислить суммарный импульс двух объектов до столкновения, их суммарный импульс после столкновения равен нулю.

m₁u₁ + м₂u₂ = 0

Когда два объекта движутся в точном направлении, что собой представляет полный импульс до столкновения является,

P_{перед столкновением} = м₁u₁ + м₂u₂

Когда два объекта движутся в противоположных направлениях, полный импульс до столкновения является,

P_{перед столкновением}= м₁u₁ + (-м₂u₂)

P_{перед столкновением}= м₁u₁ — M₂u₂

Суммарный импульс двух объектов перед столкновением

Узнайте больше о Momentum after Collision.

Предположим, что объект массой 10 кг движется со скоростью 20 м/с, а другой объект массой 15 кг движется со скоростью 25 м/с до столкновения.

i) Рассчитайте общий импульс двух объектов до столкновения, когда оба объекта движутся в одном направлении. ii) Рассчитайте общий импульс двух объектов до столкновения, когда оба объекта движутся в противоположных направлениях.

Данный:

m₁ = 15 кг

m₂ = 10 кг

u₁ = 25 м / с

u₂= 20 м / с

Найти:

P_{перед столкновением}когда оба объекта движутся в одном направлении =?

P_{перед столкновением}когда оба объекта движутся в противоположном направлении =?

Формула:

P_{перед столкновением}= м₁u₁ + м₂u₂

P_{перед столкновением}= м₁u₁ — M₂u₂

Решения:

i) Полный импульс до столкновения, когда оба тела движутся в одном направлении, используя закон сохранения импульса,

P_{перед столкновением}= м₁u₁ + м₂u₂

Подставляя все значения,

P_{перед столкновением}= 15 х 25 + 10 х 20

P_{перед столкновением}= 375 + 200

P_{перед столкновением}= 575

Общий импульс до столкновения, когда оба объекта движутся в одном направлении, составляет 575 кг · м / с.

ii) Полный импульс до столкновения, когда оба объекта движутся в противоположном направлении с использованием закон сохранения импульса,

P_{перед столкновением}= м₁u₁ — M₂u₂

Подставляя все значения,

P_{перед столкновением}= 10 х 20-15 х 25

P_{перед столкновением}= 175

Общий импульс до столкновения, когда оба объекта движутся в противоположных направлениях, составляет 175 кг · м / с.

Как рассчитать импульс до упругого столкновения

Компания импульс до упругого столкновения рассчитывается с использованием сохранения энергии.

Когда два объекта с разными массами и скоростями упруго сталкиваются друг с другом, их индивидуальная кинетическая энергия может измениться. Тем не менее, их полная кинетическая энергия остается неизменной в соответствии с законом сохранения энергии. Итак, перед упругим столкновением мы вычисляем полную энергию двух тел, складывая их кинетические энергии.

Как рассчитать моментум до эластичности и Неупругое столкновение
(Кредит: Shutterstock)

Согласно закон сохранения энергии,

KE_{перед столкновением}= КЭ_{после столкновения}

Когда мы хотим вычислить импульс двух тел до упругого столкновения их суммарный импульс после упругого столкновения P_{после столкновения} это ноль.

m₁u₁ + м₂u₂ = 0

P_{перед столкновением}= м₁u₁ + м₂u₂

Следовательно, полная кинетическая энергия после столкновения KE_{после столкновения} также равен нулю.

Следовательно, общий импульс двух объектов до столкновения является,

KE_{перед столкновением}=(1/2)м₁u₁²+(1/2) м₂u₂²

Узнайте больше о кинетической энергии.

Предположим, что два мяча массами 5 кг и 3 кг движутся в одном направлении со скоростью 10 м/с и 12 м/с и упруго сталкиваются.

i) Каков полный импульс до упругого столкновения? ii) Какова полная кинетическая энергия до упругого столкновения?

Данный:

m₁ = 5 кг

m₂ = 3 кг

u₁ = 10 м / с

u₂ = 12 м / с

Найти:

P_{перед столкновением}=?

KE_{перед столкновением}=?

Формула:

P_{перед столкновением}= м₁u₁ + м₂u₂

KE_{перед столкновением}= (1/2) м₁u₁²+(1/2) м₂u₂²

Решения:

i) Полный импульс шаров перед упругим столкновением рассчитывается с использованием сохранение импульса.

P_{перед столкновением}= м₁u₁ + м₂u₂

Подставляя все значения,

P_{перед столкновением}= 5 х 10 + 3 х 12

P_{перед столкновением}= 50 + 72

P_{перед столкновением}= 122

Общая импульс шаров до упругого удара составляет 122кг.м/с.

ii) Полная кинетическая энергия до упругого столкновения рассчитывается с использованием сохранение энергии.

KE_{перед столкновением}= (1/2) м₁u₁²+(1/2) м₂u₂²

Подставляя все значения,

KE_{перед столкновением}= (1/2)*5*10²+(1/2)*3*12²

KE_{перед столкновением}= (500/2)+(432/2)

KE_{перед столкновением}= 250 + 216

KE_{перед столкновением}= 466

Полная кинетическая энергия до упругого столкновения равна 466 Дж.

Как рассчитать импульс перед неупругим столкновением?

Импульс перед неупругим столкновением рассчитывается с использованием закона сохранения импульса.

Полная кинетическая энергия тел изменяется после неупругого столкновения. Следовательно, при неупругом столкновении энергия не сохраняется. Но мы можем вычислить общий импульс перед неупругим столкновением, сложив их индивидуальные импульсы, используя закон сохранения импульса.

Полный импульс перед неупругим столкновением определяется как

P_{перед столкновением}= м₁u₁ + м₂u₂

Узнайте больше о скорости.

Предположим, что три шара для пула массой 5 кг, 6 кг и 4 кг движутся со скоростью 8 м/с, 12 м/с и 17 м/с соответственно. Перед неупругим столкновением всех трех шариков рассчитайте суммарный импульс, когда два шарика движутся в одном направлении, а третий шарик движется в противоположном направлении.

Вычисление общего импульса шаров для пула (Кредит: Shutterstock)

Данный:

m₁ = 5 кг

m₂ = 6 кг

m₃ = 4 кг

u₁ = 8 м / с

u₂ = 12 м / с

u₃ = 17 м / с

Найти: П_{перед столкновением}=?

Формула:

P_{перед столкновением}= м₁u₁ + м₂u₂ — M₃u₃

Решения:

Суммарный импульс трех шаров для пула до неупругого столкновения рассчитывается по формуле сохранение импульса.

P_{перед столкновением}= м₁u₁ + м₂u₂ — M₃u₃

Подставляя все значения,

P_{перед столкновением}= 5 х 8 + 6 х 12 – 4 х 17

P_{перед столкновением}= 40 + 72 – 68

P_{перед столкновением}= 112 — 68

P_{перед столкновением}= 44

Суммарный импульс трех бильярдных шаров перед неупругое столкновение составляет 44кг.м/с.

Источник

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

p _1отн2— импульс первого тела относительно второго, m₁ — масса первого тела, v _1отн2 — скорость первого тела относительно второго, v ₁и v ₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Сначала переведем единицы измерения в СИ:

Изменение импульса тела

∆ p — изменение импульса тела, p — конечный импульс тела, p ₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Конечный импульс тела:

Модуль изменения импульса тела равен модулю его начального импульса:

Абсолютно упругий удар

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Пуля пробила стенку

Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:

Радиус-вектор тела повернул на 180 градусов

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Угол падения равен углу отражения:

Модуль изменения импульса в этом случае определяется формулой:

Вычисляем:

Второй закон Ньютона в импульсном виде

Подставим это выражение во второй закон Ньютона и получим:

F ∆t — импульс силы, ∆ p — изменение импульса тела

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Второй закон Ньютона в импульсном виде:

Второй закон Ньютона для ракеты:

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

Выразим ускорение из второго закона Ньютона для ракеты:

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

Отсюда скорость равна:

Импульс частицы до столкновения равен − p ₁, а после столкновения равен − p ₂, причём p₁ = p, p₂ = 2p, − p ₁⊥ − p ₂. Изменение импульса частицы при столкновении Δ − p равняется по модулю:

Алгоритм решения

Решение

Запишем исходные данные:

Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δ p = √ p 2 1 + p 2 2

Подставим известные данные:

Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Модуль изменения импульса движение по окружности

iSopromat.ru

Пример решения задачи по определению импульса сил, действующих, за определенное время, на материальную точку заданной массы, движущуюся по окружности с постоянной скоростью.

Задача

Материальная точка массой m=10 г движется по окружности с постоянной скоростью 40 см/с.

Найти импульс сил, действующих на точку за время прохождения точкой половины окружности (рисунок 2.3).

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Сначала переведем единицы измерения в СИ:

Изменение импульса тела

∆ p — изменение импульса тела, p — конечный импульс тела, p ₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Конечный импульс тела:

Модуль изменения импульса тела равен модулю его начального импульса:

Абсолютно упругий удар

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Пуля пробила стенку

Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:

Радиус-вектор тела повернул на 180 градусов

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Модули конечной и начальной скоростей равны:

Модули конечного и начального импульсов равны:

Угол падения равен углу отражения:

Модуль изменения импульса в этом случае определяется формулой:

Вычисляем:

Второй закон Ньютона в импульсном виде

Подставим это выражение во второй закон Ньютона и получим:

F ∆t — импульс силы, ∆ p — изменение импульса тела

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Второй закон Ньютона в импульсном виде:

Второй закон Ньютона для ракеты:

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

Выразим ускорение из второго закона Ньютона для ракеты:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

Отсюда скорость равна:

Импульс частицы до столкновения равен − p ₁, а после столкновения равен − p ₂, причём p₁ = p, p₂ = 2p, − p ₁⊥ − p ₂. Изменение импульса частицы при столкновении Δ − p равняется по модулю:

Алгоритм решения

Решение

Запишем исходные данные:

Δ p = √ p 2 1 + p 2 2

Подставим известные данные:

Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5

pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

§ 7.6. Другая форма уравнения движения материальной точки по окружности

При рассмотрении кинематики движения точки по окружности (см. § 27 гл. 1) было установлено, что ускорение точки целесообразно разложить на нормальную _n и тангенциальную _τ составляющие, модули которых соответственно равны:

Нормальная составляющая характеризует изменение скорости только по направлению, а тангенциальная — только по модулю. Соответственно второй закон Ньютона для проекций _n и _τ ускорения запишется так:

где F_n — проекция силы на направление, перпендикулярное скорости, a F_τ — проекция силы на направление скорости.

Второе из этих уравнений перепишем, используя связь тангенциального α_τ и углового β ускорений (α_τ = βR):

Момент силы

Пусть к материальной точке приложена сила, действующая в плоскости движения.

Угловое ускорение, как это следует из уравнения (7.6.1), определяется тангенциальной составляющей силы . Например, силы ₁, ₂, ₃ (рис. 7.30) создают одно и то же ускорение β, так как для них составляющие _τ одинаковы.

Обозначим через α угол между вектором силы и радиусом-вектором рассматриваемой материальной точки. Тогда

Назовем расстояние d между центром окружности О и линией действия силы плечом силы. Из рисунка 7.31 видно, что

В частности, для силы F₁ (см. рис. 7.30) угол α = 90° и, следовательно, d₁ = R, т. е. плечо силы равно радиусу окружности.

Произведение модуля F_τ тангенциальной составляющей на радиус R назовем моментом силы и обозначим буквой М.

Из формул (7.6.2) и (7.6.3) следует, что

Запишем уравнение (7.6.1) в другой форме, используя понятие момента силы. Для этого умножим левую и правую части этого уравнения на R. На основании равенства (7.6.4) получим:

Таким образом, при постоянных значениях m и R момент силы определяет угловое ускорение.

Однако с таким же успехом при заданном R угловое ускорение может определяться величинами F_τR 2 , F_τR 3 и т. д. Поэтому возникает вопрос о том, почему мы выбираем в качестве характеристики силового воздействия именно момент силы М = F_τR, а не какую-либо другую комбинацию величин F_τ, R. Причина такого выбора состоит в следующем.

Сравним движение материальной точки по окружности с прямолинейным движением. Между кинематическими характеристиками в этих случаях имеется следующее соответствие: линейному перемещению Δs соответствует угловое перемещение Δφ, линейной скорости v — угловая скорость ω, линейному ускорению а — угловое ускорение β.

Каково же будет соответствие между динамическими характеристиками? Начнем с силы. Рассмотрим выражение для работы. При движении по окружности работа совершается тангенциальной составляющей ₁ силы. Нормальная составляющая не совершает работы.

Таким образом, при перемещении по окружности на малое расстояние Δs (рис. 7.32) совершается элементарная работа

Введем вместо линейной характеристики перемещения Δs угловое Δφ. Они связаны равенством Δs = RΔφ.

Используя это соотношение, перепишем выражение (7.6.6) в виде:

Отсюда следует, что если вместо линейного перемещения использовать угловое, то роль силы будет играть величина F_τR, т.е. момент силы М.

Знак момента силы

В определении момента силы (7.6.4) не учтено, что сила имеет направление и может как увеличивать угловую скорость, так и уменьшать ее. Это обстоятельство можно учесть так. Будем считать одно из направлений обращения точки, например против движения часовой стрелки, положительным. Тогда моменту силы условимся приписывать знак плюс, если сила увеличивает скорость обращения точки в направлении против часовой стрелки, и знак «минус» в противоположном случае.

Момент инерции

Мы установили, что при описании движения по окружности вместо величин г, v, a, F удобнее использовать величины φ, ω, β, М. Какая же величина соответствует массе? Из уравнения (7.6.5) видно, что роль массы при движении по окружности играет величина mR 2 . Назовем ее моментом инерции и обозначим буквой J:

Используя это обозначение, запишем уравнение движения материальной точки по окружности в форме:

Итак, мерой инертности при движении материальной точки по окружности служит момент инерции. То, что инертность при движении по окружности зависит от радиуса, легко почувствовать. Например, камень на длинной веревке раскрутить труднее, чем на короткой.

Подчеркнем еще раз, что исходное уравнение движения mа₁ = F₁ и уравнение (7.6.9) эквивалентны. Использование того или иного из них при описании движения материальной точки определяется соображениями удобства и простоты.

Момент импульса

В главе 2, посвященной второму закону Ньютона, были рассмотрены две формы записи уравнения движения:

Из второго уравнения (7.6.10) следует, что изменение вектора импульса m определяется импульсом силы dt. Такая форма записи очень удобна при решении многих задач.

Запишем в соответствующем виде уравнение движения материальной точки по окружности. Для этого преобразуем левую часть уравнения (7.6.9).

По определению угловое ускорение . Учитывая, что момент инерции материальной точки J = mR 2 не зависит от времени, можем записать:

Выясним физический смысл величины Jω. Перепишем это выражение в иной форме. Так как J = mR 2 и Rω = v, то

Выражение mvR естественно назвать моментом импульса.

Используя равенство (7.6.11), уравнение (7.6.9) можем записать в виде:

Приходим к выводу: изменение момента импульса определяется импульсом момента силы, т. е. величиной Mdt.

Для момента импульса будем использовать специальное обозначение Jω = L. Тогда уравнение (7.6.13) примет вид:

где L = Jω = mvR — момент импульса. Скоро мы увидим, что момент импульса, подобно импульсу, сохраняется в замкнутых системах.

Для динамического описания движения материальной точки по окружности мы ввели новые величины: момент силы, момент инерции и момент импульса. Был записан второй закон Ньютона в новой форме. Эта форма чрезвычайно удобна для перехода к динамике вращательного движения твердого тела.

I. Механика

Тестирование онлайн

Импульс тела

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Импульс силы численно равен площади фигуры под графиком F(t).

Если же сила непостоянная во времени, например линейно увеличивается F=kt, то импульс этой силы равен площади треугольника. Можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину за тот же промежуток времени

источники:

http://b4.cooksy.ru/articles/modul-izmeneniya-impulsa-dvizhenie-po-okruzhnosti

http://fizmat.by/kursy/zakony_sohranenija/impuls

Источник

Закон сохранения импульса на плоскости

Теория
Задачи
Задача 1
Задача 2.
Задача 3.
Задача 4.

Из кодификатора по физике, 2020.
«1.4.3. Закон сохранения импульса: в ИСО

Теория

Импульс тела — векторная физическая величина, равная произведению массы тела m на его скорость :

— Обозначается буквой , измеряется в килограмм-метр в секунду (кг∙м/с).
— Импульс тела направлен в ту же сторону, что и скорость тела, и наоборот.

Изменение импульса тела

где и $overrightarrow { { p }_{ 0 } }$ — конечный и начальный импульсы тела, и $overrightarrow { { upsilon }_{ 0 } }$ — конечная и начальная скорости тела, m — масса тела.

Импульс системы тел равен векторной сумме импульсов тел $overrightarrow { { p }_{ 1 } } ,overrightarrow { { p }_{ 2 } } ,...,$ входящих в эту систему

где m1, m2, … — массы тел системы, $overrightarrow { { upsilon }_{ 1 } } ,overrightarrow { { upsilon }_{ 2 } } ,...$ — скорости тел системы.

Изменение импульса системы тел

где $overrightarrow { { p }_{ 1 } } ,overrightarrow { { p }_{ 2 } } ,...$ — конечный импульс системы тел, $overrightarrow { { p }_{ 01 } } ,overrightarrow { { p }_{ 02 } } ,...$ — начальный импульс системы тел, m1, m2, … — массы тел системы, $overrightarrow { { upsilon }_{ 1 } } ,overrightarrow { { upsilon }_{ 2 } } ,...$ — конечные скорости тел системы, $overrightarrow { { upsilon }_{ 01 } } ,overrightarrow { { upsilon }_{ 02 } } ,...$ — начальные скорости тел системы.

Импульс силы — векторная физическая величина, равная произведению силы на время t ее действия:

— Обозначается буквой , измеряется в Ньютон на секунду (Н∙с).
— Импульс силы направлен в ту же сторону, что и сила, и наоборот.

Закон сохранения импульса:

в инерциальной системе отсчета (ИСО) векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю.

Задачи на применение закона сохранения импульса тел (системы тел) решайте, придерживаясь следующего плана:

1. Сделайте схематический чертеж. Укажите направления осей координат ОX и ОY.

— Материальную точку изобразите в виде двух прямоугольников (или окружностей) и укажите над ними (если это известно) направления скорости или импульса до и после взаимодействия.
— Индексы скоростей, импульсов на рисунке должны соответствовать индексам скоростей, импульсов в условии.

2. Определите, векторная сумма внешних сил, действующих на систему тел, равна нулю или нет. Если равна нулю, то запишите закон сохранения импульса тел в векторном виде и в проекциях.

Определите значения проекций всех величин.

3. Решите полученные уравнения.

к оглавлению ▴

Задачи

Задача 1

Два тела движутся по взаимно перпендикулярным пересекающимся прямым, как показано на рисунке. Модуль импульса первого тела p₁ = 4 кг⋅м/с, а второго тела p₂ = 3 кг⋅м/с . Чему равен модуль импульса системы этих тел после их абсолютно неупругого удара?

Решение. Импульс тел изменяет их столкновение. До удара двигались тела отдельно друг от друга. После неупругого удара тела двигались вместе.

Внешних сил нет, поэтому запишем закон сохранения импульса

1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда импульс тел (направление которого неизвестно) будет равен (рис. 2, а)

Направление осей OХ и OY показаны на рисунке условия. Запишем уравнение (1) в проекциях на оси:

После подстановки уравнений (3) и (4) в (2) получаем:

2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 2, б). Модуль импульса p после удара найдем по теореме Пифагора

к оглавлению ▴

Задача 2.

По гладкой горизонтальной плоскости движутся вдоль осей X и Y две шайбы с импульсами, равными по модулю p10 = 5 кг·м/с и p20 = 3 кг·м/с (рис. 3). После их соударения первая шайба продолжает двигаться по оси Y в прежнем направлении. Модуль импульса первой шайбы после удара равен p1 = 2 кг·м/с. Найдите модуль импульса второй шайбы после удара. Ответ округлите до десятых.

Решение. Импульс шайб изменяет их столкновение. До удара шайбы двигались отдельно друг от друга. После удара шайбы так же двигались отдельно.

Внешних сил нет, поэтому запишем закон сохранения импульса

1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда импульс вто-рой шайбы (направление которого неизвестно) будет равен

Направление осей OХ и OY показаны на рисунке 4. Запишем уравнение (1) в проекциях на оси:

После подстановки уравнений (3) и (4) в (2) получаем:

к оглавлению ▴

Задача 3.

Лодка массой 100 кг плывет без гребца вдоль пологого берега со скоростью 1 м/с. Мальчик массой 50 кг прыгает с берега в лодку со скоростью 2 м/с так, что векторы скорости лодки и мальчика составляют прямой угол. Определите значение и направление скорости лодки (в см/с) с мальчиком. Ответ округлите до целых.

Решение. Скорость лодки изменяет прыжок мальчика. До прыжка двига-лись лодка и мальчик отдельно друг от друга. После прыжка мальчик и лодка двигались вместе.

Векторная сумма внешних сил (силы тяжести и силы реакции опоры) равна нулю, поэтому запишем закон сохранения импульса

1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда скорость лодки с мальчиком (направление которой неизвестно) будет равна

Направим ось OХ вдоль начальной скорости лодки, ось OY — вдоль начальной скорости мальчика, т.к. векторы скорости лодки и мальчика составляют прямой угол (рис. 5, а). Запишем уравнение (1) в проекциях на оси:

После подстановки уравнений (3) и (4) в (2) получаем:

Направление скорости υ определим следующим образом (рис. 5, б):

Примечание. Угол α можно было определить и через другие формулы

2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 5, в). Модуль скорости υ после прыжка найдем по теореме Пифагора

Направление скорости υ определим следующим образом (см. рис. 5, в):

к оглавлению ▴

Задача 4.

Летящий снаряд разрывается на два осколка, при этом первый осколок летит со скоростью 50 м/с под углом 90° по отношению к направлению движения снаряда, а второй — со скоростью 200 м/с под углом 30°. Найдите отношение массы первого осколка к массе второго осколка.

Скорость снаряда изменяет взрыв. До взрыва двигался только снаряд. После взрыва осколки снаряда двигались отдельно друг от друга.

Внешних сил нет, поэтому запишем закон сохранения импульса

1 способ (координатный). Направим ось OХ вдоль начальной скорости снаряда, ось OY — вдоль конечной скорости первого осколка (рис. 6, а). Запишем уравнение (1) в проекции на ось:

2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 6, б). Тогда из прямоугольного треугольника получаем

Автор Сакович А.Л.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Закон сохранения импульса на плоскости» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Баканина Л. Закон сохранения импульса при соударениях // Квант. – 1977. – № 3. – С. 46-51.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Закон сохранения импульса (количества движения) выполняется для замкнутых систем, то есть таких, которые включают в себя все взаимодействующие тела, так что ни на одно из тел системы не действуют внешние силы. Однако при решении многих физических задач оказывается, что импульс может оставаться постоянным и для незамкнутых систем. Правда, в этом случае количество движения сохраняется лишь приближенно. Попытаемся разобраться, в чем тут дело.

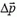
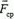
Изменение импульса незамкнутой системы равно суммарному импульсу внешних сил. Обозначим через среднее значение результирующей внешней силы, действующей на систему в течение промежутка времени Δt. Тогда

Если абсолютная величина этой силы не слишком велика и время, в течение которого действует сила, мало, то произведение 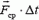тоже будет малым. В таком случае возникает необходимость оценки, с какой точностью можно считать импульс системы неизменным.

Кроме того, не следует забывать, что импульс — вектор, и, следовательно, можно говорить о сохранении проекции этого вектора на какое-либо направление. Действительно, если система не замкнута, но внешние силы таковы, что сумма проекций всех сил на некоторое направление равна нулю, то проекция импульса системы на это направление остается величиной постоянной. Незамкнутая система в этом направлении аналогична замкнутой.

Кратковременные взаимодействия возникают, например, при взрывах, выстрелах, соударениях. Такого типа задачи мы и обсудим. Постараемся в каждом конкретном случае выяснить, выполняется или не выполняется закон сохранения импульса и от чего это зависит.

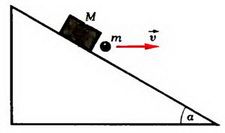
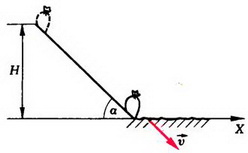
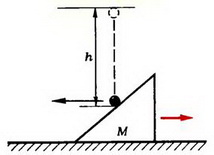
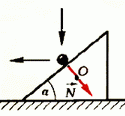
Задача 1. Из пушки, соскальзывающей без трения по наклонной плоскости и прошедшей уже путь l, производится выстрел в горизонтальном направлении (рис. 1). При какой скорости снаряда пушка остановится после выстрела? Масса снаряда m много меньше массы пушки M, угол наклона плоскости α.

Перед выстрелом пушка (вместе со снарядом), прошедшая путь l, имеет импульс 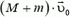, направленный вдоль наклонной плоскости. Модуль этого импульса можно найти из закона сохранения энергии:

Сразу после выстрела пушка остановилась, а снаряд полетел в горизонтальном направлении. Таким образом, несмотря на кратковременность взаимодействия пушки и снаряда, импульс этой системы не сохраняется. Почему же?

Во время выстрела резко возрастает сила давления пушки на наклонную плоскость, а значит, возрастает и сила реакции со стороны плоскости, так что импульс этой силы оказывается достаточно большим. Он то и изменяет суммарный импульс пушки и снаряда.

Рис. 1.

Однако в направлении вдоль наклонной плоскости проекция силы реакции равна нулю, а проекция импульса силы тяжести 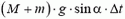за малое время выстрела Δt мала и при выстреле не увеличивается. Поэтому можно, с некоторой степенью точности, считать, что в направлении вдоль наклонной плоскости проекция количества движения системы пушка — снаряд сохраняется. Следовательно, проекция суммарного импульса пушки и снаряда до выстрела равна проекции снаряда после выстрела (пушка покоится):

Отсюда модуль скорости снаряда непосредственно после выстрела

При решении этой задачи мы полагали, что в направлении вдоль наклонной плоскости система пушка — снаряд ведет себя как замкнутая система. Однако оценить, с какой степенью точности это справедливо, мы не можем, так как система взаимодействующих тел сложная и нет необходимых данных для такой оценки.

Разберем теперь две задачи с более простым взаимодействием, где такую оценку можно сделать.

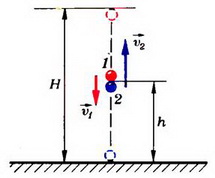
Задача 2. В деревянный шар массы M = 1 кг, падающий вниз со скоростью V₀ = 1 м/c, стреляют снизу из ружья и пробивают его насквозь. Какую скорость будет иметь шар сразу после этого? Скорость пули υ₀ = 300 м/с, после вылета из шара υ = 100 м/с, масса пули m = 10 г.

Оценим, с какой точностью можно считать систему шар — пуля замкнутой во время их взаимодействия. Другими словами, выясним, можно ли пренебречь импульсом силы тяжести за это время.

Время взаимодействия 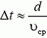, где d — диаметр шара, a υ_ср — средняя скорость пули внутри шара. Диаметр шара можно оценить, зная, что плотность дерева ρ приблизительно равна плотности воды ρ_в = 10³ кг/м³:

Таким образом, Δt ≈ 5·10^–4 c. Импульс силы тяжести системы за это время (а значит, и изменение суммарного импульса шара и пули)

p = (M + m)·g·Δt ≈ 5·10^–3 Н·с.

Количество движения системы перед взаимодействием

p₀ = m·υ₀ – M·V₀ = 2 Н·с.

Тогда отношение

и, следовательно, с точностью до 0,2 % можно считать, что во время взаимодействия импульс системы не изменяется.

Запишем закон сохранения для проекции импульса на ось, направленную вертикально вверх:

или

m·υ₀ – M·V₀ = m·υ+ M·V_y.

Отсюда проекция скорости шара после взаимодействия

то есть шар начнет двигаться вверх со скоростью 1 м/сек.

Задача 3. Шарик бросают вертикально вверх со скоростью υ₀ = 1 м/с. Когда он достиг верхней точки своего подъема, бросают еще такой же шарик с начальной скоростью 2υ₀. Определить скорости шариков после столкновения, если столкновение можно считать абсолютно упругим.

Аналогично предыдущей задаче прежде всего оценим, с какой степенью точности систему двух шариков во время соударения можно считать замкнутой. Для этого найдем импульс системы до удара, импульс силы тяжести за время удара и сравним их между собой.

Пусть шарики столкнулись на высоте h через время t после начала движения второго шарика (рис. 2). Тогда для первого шарика

где 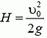— максимальная высота подъема. Для второго шарика

Рис. 2.

Отсюда 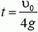, и скорости обоих шариков непосредственно перед столкновением равны

причем первый шарик движется вниз, а второй — вверх.

Итак, количество движения системы до взаимодействия

p₀ = m·υ₂ – m·υ₁ = 1,5m·υ₀.

Теперь попытаемся оценить время взаимодействия и импульс силы тяжести за это время. Для этого мы должны представить себе, как происходит процесс соударения. Рассмотрим вначале соударение торцами двух одинаковых стержней. При ударе в торце возникает упругая деформация, которая распространяется вдоль стержня, то есть в стержне возникает звуковая волна. Дойдя до противоположного конца стержня, волна отражается и возвращается обратно. Можно сказать, что на этом процесс соударения заканчивается, и время взаимодействия стержней равно времени прохождения звуковой волны вдоль стержня и обратно. На самом деле картина взаимодействия гораздо сложнее, а в случае шариков, где возникающая упругая волна не плоская, — тем более. Однако для оценки и здесь будем считать, что с точностью до порядка величины время соударения равно времени распространения звуковой волны внутри шарика: 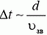. 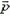Скорость звука в твердых телах порядка нескольких километров в секунду. Если диаметр шарика порядка сантиметра, то Δt ~ 10^–5 c, и импульс силы тяжести по абсолютной величине во много раз меньше импульса шариков до взаимодействия:

Таким образом, и в этом случае мы можем считать систему соударяющихся шариков замкнутой. (Конечно, дальнейшее движение шариков существенно зависит от силы тяжести.) Так как удар шариков абсолютно упругий, воспользуемся законами сохранения механической энергии и проекции импульса на ось, направленную вертикально вверх:

Подставив сюда соответствующие значения для υ₁ и υ₂:

найдем

— при упругом ударе шарики равных масс обмениваются скоростями.

Не следует, однако, думать, что всегда при соударениях можно пренебречь действием внешних сил и считать систему замкнутой. Для примера рассмотрим такую задачу.

Задача 4. Мешок с мукой сползает без начальной скорости с высоты Н по гладкой доске, наклоненной подуглим α = 60° к горизонту. После спуска мешок попадает на горизонтальный шероховатый пол. Коэффициент трения мешка о пол μ = 0,7. Где остановится мешок?

После спуска с доски мешок имеет скорость 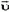, направленную вдоль доски (рис. 3). Ее абсолютную величину можно найти из закона сохранения механической энергии, так как доска гладкая и потерь энергии нет:

Рис. 3.

В горизонтальном направлении на мешок действует сила трения скольжения, модуль которой 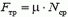. Импульс этой силы за время удара равен

то есть не зависит ни от того, но какому закону изменяется сила реакции опоры (aзначит, и сила давлении мешка на пол), ни от времени соударения. Найдем изменение горизонтальной проекции импульса мешка. Направим ось X по горизонтали вправо, тогда, согласно второму закону Ньютона,

или

Отсюда проекция скорости, с которой мешок начнет двигаться по полу,

Что означает знак «минус»? Формально знак «минус» говорит о том, что после удара мешок должен двигаться влево, или, другими словами, что импульс силы трения оказался больше первоначальной горизонтальной проекции импульса мешка. Значит, в какой-то момент в процессе соударения проекция скорости мешка на ось Х обратилась в нуль. Начиная с этого момента, наше решение становится неверным. Действительно, модуль силы трения равен μ·N_cp только при скольжении, а в состоянии покоя сила трения может принимать любые значения от 0 до μ·N_cp в зависимости от того, какие силы (кроме силы трения) действуют на тело. В нашем случае никакие другие силы не имеют проекций в горизонтальном направлении, следовательно, в тот момент, когда горизонтальная проекция скорости мешка обратилась в нуль, сила трения тоже обращается в нуль. Таким образом, мешок по полу вообще двигаться не будет.

Наконец, обсудим еще одну достаточно известную задачу на соударение тел. При решении этой задачи обычно используют довольно грубые приближения, никак не оговаривая при этом ни то, что это приближение, ни при каких условиях им можно пользоваться.

Задача 5. На стоящий на гладкой горизонтальной поверхности клин массы М с высоты h падает шар массы m и отскакивает в горизонтальном направлении (рис. 4). Найти горизонтальную проекцию скорости клина 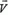после удара. Трением пренебречь, удар считать абсолютно упругим.

В отличие от всех предыдущих задач здесь нужно рассматривать соударение не двух, а трех тел — шарика, клина и горизонтальной плоскости. В общем случае, не делая никаких дополнительных предположений о механизме удара, решить эту задачу нельзя. В наиболее распространенном решении этой задачи неявно (без всяких оговорок) предполагается, что соударения шарика с клином и клина с горизонтальной плоскостью происходят одновременно, а клин после соударения имеет только горизонтальную проекцию скорости. Затем записываются уравнения законов сохранения механической энергии и импульса:

где V_x и υ_x — соответственно проекции скоростей клина и шарика на горизонтальную ось, направленную вправо. Отсюда

Рис. 4.

Однако в таком решении совершенно не ясно, куда делась вертикальная проекция импульса шарика. Ведь если соударение абсолютно упругое, вертикальная проекция импульса системы не исчезает, а лишь меняет знак! Шарик после удара отскакивает в горизонтальном направлении, плоскость вообще неподвижна. Значит, клин после удара обязательно должен подпрыгнуть. А энергия, связанная с этим движением, в приведенном решении не учитывается.

Физической картине удара больше соответствует предположение о том, что вначале шарик соударяется только с клином, а потом клин, получивший некоторую скорость в результате этого соударения, взаимодействует с горизонтальной плоскостью. После первого соударения вертикальная проекция скорости клина

а горизонтальные проекции скоростей клина и шарика, как и в первом решении, связаны соотношением

или

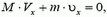
Тогда закон сохранения энергии можно записать в виде

Подставив сюда соответствующие выражения для υ_x и V_y, найдем горизонтальную проекцию скорости клина:

Таким образом, задачу о соударении трех тел мы свели к задаче двух последовательных попарных соударений (второе соударение для решения задачи нам не понадобилось). При этом мы считали, что клин после соударения с шариком движется чисто поступательно. Это может быть только в том случае, если сила давления шарика 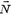во время удара проходит через центр тяжести О клина (рис. 5).

Рис. 5.

Кроме того, заметим, что для того чтобы шарик после соударения отскочил горизонтально, угол клина α должен иметь вполне определенную величину, зависящую от масс шарика и клина.

В заключение предлагаем несколько задач для самостоятельного решения.

Упражнения

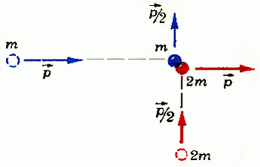
1. В центр шара массы m₁ = 300 г, лежащего на краю стола, попадает горизонтально летящая пуля массы m₂ = 10 г и пробивает его насквозь. Шар падает на пол на расстоянии s₁ = 6 м от стола, а пуля — на расстоянии s₂ = 15 м. Высота стола H = 1 м. Определить первоначальную скорость пули.

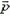
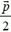
2. Две частицы с массами m и 2m, имеющие импульсы и , движутся по взаимно перпендикулярным направлениям. После соударения частицы обмениваются импульсами (рис. 6). Определить выделившееся при ударе количество теплоты.

Рис. 6.

3. Мешок с мукой сползает без начальной скорости с высоты Н = 2 м по доске, наклоненной под углом α= 45° к горизонту. После спуска мешок попадает на горизонтальную поверхность. Коэффициент трения мешка о доску и горизонтальную поверхность μ = 0,5. На каком расстоянии от конца доски остановится мешок?

Ответы

Источник

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

Каков импульс автомобиля массой 60 кг, движущегося со скоростью 120 км/ч до столкновения с другими транспортными средствами?

Как найти общий импульс двух тел перед столкновением?

Предположим, что объект массой 10 кг движется со скоростью 20 м/с, а другой объект массой 15 кг движется со скоростью 25 м/с до столкновения.

Как рассчитать импульс до упругого столкновения

Предположим, что два мяча массами 5 кг и 3 кг движутся в одном направлении со скоростью 10 м/с и 12 м/с и упруго сталкиваются.

i) Каков полный импульс до упругого столкновения? ii) Какова полная кинетическая энергия до упругого столкновения?

Как рассчитать импульс перед неупругим столкновением?

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

Модуль изменения импульса движение по окружности

iSopromat.ru

Задача

Импульс тела, закон сохранения импульса

теория по физике 🧲 законы сохранения

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

§ 7.6. Другая форма уравнения движения материальной точки по окружности

Момент силы

Знак момента силы

Момент инерции

Момент импульса

I. Механика

Тестирование онлайн

Импульс тела

Импульс силы

Изменение импульса тела

Главное запомнить

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Закон сохранения импульса на плоскости

Теория

Задачи

Задача 1

Задача 2.

Задача 3.

Задача 4.

Не пропустите также: