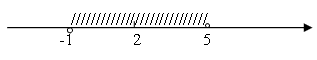В материалах ГИА, ЕГЭ и на вступительных экзаменах в ВУЗы из года в год предлагаются различные задания, в формулировках которых присутствует модуль. Популярность темы «Модуль» обусловлена теми свойствами, которыми обладает модуль числа. Однако многие из этих свойств совершенно не отражены в школьной программе. Задания на отыскание корней уравнений содержащих модуль вызывают у многих учащихся затруднения. Связано это с тем, что тема «Модуль» требует со стороны учащихся глубокого и досконального исследования.
Для решения уравнений с модулем используется несколько способов – алгебраический, графический, метод интервалов, последовательное раскрытие модулей.
Рассмотрим все эти методы решения на конкретных примерах.
Пример 1.
Найти произведение целых корней уравнения
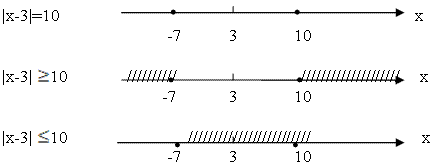
√(х2 + 6х + 9) + √(х2 + 2х + 1) = 2.
Так как исходное уравнение можно переписать в виде
√(х + 3)2 + √(х + 1)2 = 2 и пользуясь правилом √а2 = |a| имеем
|х + 3| + |х + 1|= 2.
Рассмотрим решение этого уравнения, используя геометрический смысл модуля, применение которого позволяет устно решать уравнения вида
|х ± а| + |х ± b|= c.
Пусть точка М на координатной оси имеет координату m, а точка N – n, тогда расстояние между точками M и N равно значению выражения |m – n|, MN = |m – n| (рис. 1).
Рассмотрим выражение |х + 3| = |x – (-3)| и |х + 1| = |x – (-1)|. Пусть точка А имеет координату х, точка В – координату -3, а точка С – координату -1, тогда АВ = |x – (-3)|; АС = |x – (-1)| и АВ + АС = |х + 3| + |х + 1|, но |х + 3| + |х + 1|= 2, т.е. АВ + АС = 2. Другими словами, нам необходимо найти все значения х, при которых сумма расстояний АВ и АС была бы равна двум.
Рассмотрим возможные случаи расположения точки А относительно точек В и С:
1) х < -3 (рис. 2), тогда АВ + АС > BC, но ВС = 2, значит АВ + АС > 2;
2) х = -3 (рис. 3), тогда АВ + АС = 0 + 2 = 2, т.е. х = -3 – корень уравнения;
3) -3 < х < -1 (рис. 4), тогда АВ + АС = ВС = 2, т.е. все числа из промежутка (-3; 1) являются корнями данного уравнения;
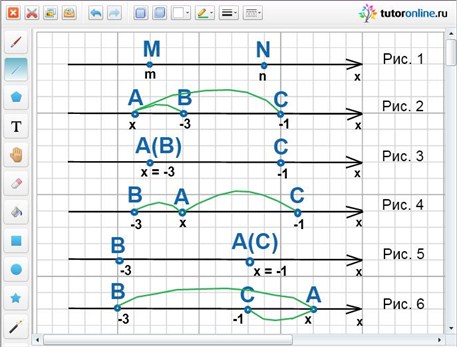
4) х = -1 (рис. 5), тогда АВ + АС = 2 + 0 = 2, т.е. х = -1 – корень уравнения;
5) х > -1 (рис. 6), тогда АВ + АС > BC, значит АВ + АС > 2.
Таким образом, корнями данного уравнения являются все числа из отрезка [-3; -1].
Целые корни: -3; -2; -1.
Их произведение: -3 · (-2) · (-1) = -6.
Заметим, что исходное уравнение можно было решить также с помощью метода промежутков.
Пример 2.
Найти количество корней уравнения |x – 1| + |x + 2| = 1.
Решение.
Решим данное уравнение тремя способами.
I способ. Наиболее распространенным методом решения данного типа уравнений является метод промежутков.
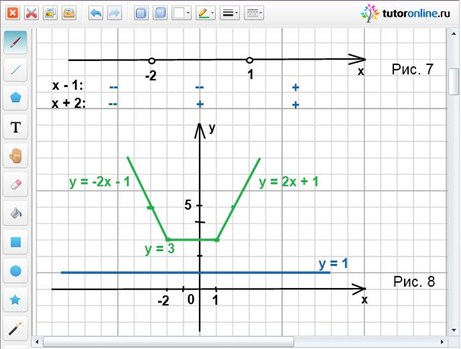
Найдем нули подмодульных выражений (это числа 1 и -2) и отметим их на числовой оси. На каждом из трех полученных промежутков найдем знаки подмодульных выражений (рис. 7).
С помощью рисунка раскроем модули в исходном уравнении:
1) x < -2, тогда -x + 1 – x – 2 = 1; -2х = 2; x = -1. Данный корень не удовлетворяет условию рассматриваемого интервала, поэтому в данном случае нет корней.
2) -2 ≤ x ≤ 1, имеем -х + 1 + х + 2 = 1; 3 = 1. Равенство не верное, поэтому корней нет.
3) х > 1, тогда х – 1 + х + 2 = 1; 2х = 0; х = 0. Условие х > 1 не выполняется, поэтому х = 0 корнем не является.
Наше уравнение корней не имеет.
II способ. При подготовке к ГИА и ЕГЭ необходимо овладеть навыками построения графиков различных функций, в том числе и функций вида y = |f1(x)| + |f2(x)| + … + |fn(x)|.
Итак, решим уравнение |x – 1| + |x + 2| = 1 графически (рис. 
. Для этого построим графики функций y = 1 (прямая, параллельная оси абсцисс и проходящая чрез точку (0; 1)) и y = |x – 1| + |x + 2|.
Раскроем модули:
1) x < -2, тогда y = -x + 1 – x – 2; y = -2х – 1.
2) -2 ≤ x ≤ 1, y = –х + 1 + х + 2; y = 3.
3) х > 1, тогда y = х – 1 + х + 2; y = 2х + 1.
Графики не имеют общих точек, значит, уравнение не имеет корней.
Заметим, что график функции y = |x – 1| + |x + 2| можно было построить, не раскрывая модули. Так как y = -2x – 1; y = 3; y = 2x + 1 – линейные функции, то для построения х графиков достаточно двух точек.
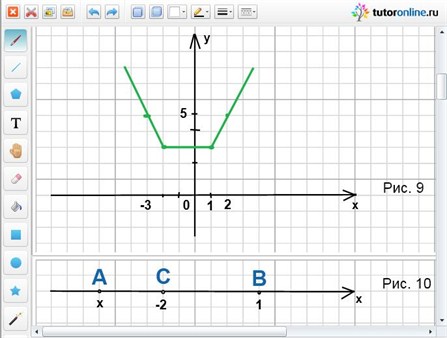
Найдем значение функции y = |x – 1| + |x + 2| в нулях подмодульных выражений: y(1) = 3 и y(-2) = 3. Выберем удобные для вычисления два значения аргумента, одно из которых меньше -2, а второе больше 1, и найдем соответствующие значения функции: y(-3) = 5; y(2) = 5.
Отметим полученные точки на координатной плоскости и построим график (рис. 9).
III способ. Наиболее рациональным решением, позволяющим устно ответить на вопрос задачи, является использование геометрического смысла модуля.
|x – 1| + |x + 2| = 1.
Отметим на координатной прямой точки А(х); В(1); С(-2), тогда АВ = |x – 1|; AC = |x + 2| (рис. 10).
То есть необходимо найти все значения х, при которых сумма расстояний АС и ВС равна 1 (|x – 1| + |x + 2| = 1), но АС + АВ не может быть меньше, чем длина отрезка ВС, а ВС = |1 – (-2)| = 3. Таким образом, уравнение не имеет корней.
Ответ: 0.
Различные методы решения уравнений с модулем ни в коем случае не противопоставляются друг другу. Наоборот, наиболее успешным в решении может быть именно разумное их сочетание. Тогда и на экзаменах не будет случаев, когда из-за громоздких вычислений на решение одного простого задания будет потрачена уйма времени.
Остались вопросы? Не знаете, как решать уравнения с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Цель: рассмотреть геометрическое определение модуля. Уметь применять его для решения
уравнений и неравенств с модулем, развивать умение исследовать уравнения с параметрами.
Ход урока
1. Организационная
часть (Цель занятия)
2. Актуализация
знаний
- Алгебраическое определение модуля
|a| =
- Вычислите модули чисел: 3, -8, 10, 0.
- Решите уравнения
|x| = 4 |x| = -4 |x| = 0 - Решите неравенства
|x| > 5 |x| < 5 - Запишите к каждому чертежу соответствующее
уравнение или неравенство
3. Изучение
нового материала
- Найдите расстояние между двумя точками координатной прямой
А) А(-1) и В(3)
Б) Р(0,0001) и Q(132)
В) М(-2) и N(-87) - Формула расстояния между двумя точками координатной прямой
с координатами х и а:
ρ(x,a) = |x — a|Геометрическое истолкование выражения |x-a|- это расстояние между двумя точками
координатной прямой. - Отметить на координатной прямой точки, для которых
|x| = 1
|x| ≥ 3
|x| > 2
1 < |x| < 4
|x| = 0
|x| = -1
- Каков смысл выражений?
Изобразите множества,
задаваемые этими предложениями на координатной прямой. Иными словами переведем
аналитические модели на геометрический язык. - Решим неравенство |х-2| <3
Переведем аналитическую модель на
геометрический язык: нужно найти на координатной прямой такие точки х, которые
удовлетворяют условию ρ (х,2) < 3. Другими словами удалены от точки с
координатой 2 на расстояние меньше 3.Это все точки, принадлежащие интервалу (-1;5)
Ответ: (-1;5)
- Как решить уравнение?
|х-5|+|х+1|=8
Выражение |х-5| можно
истолковать, как расстояние между точками с координатами х и 5.Выражение |х+1| можно
истолковать, как расстояние между точками с координатами х и -1.Тогда уравнение означает, что нужно найти такую точку Х(х), сумма расстояний
от которой до точек с
координатами 5 и -1 равна 8.Расстояние между точками с координатами 5 и -1 равно 6 < 8, следовательно,
точка с координатой х находиться вне отрезка [-1;5] и таких точек две.Ответ: х=-2, х=6
Что произойдет,
если вместо 8 взять число 1, 6, 100,…? Сколько будет тогда корней уравнения?При равенстве суммы модулей 1 – нет решений, так как 1<6.
При равенстве суммы модулей 6 – множество решений, так как
все точки отрезка [-2;6] удовлетворяют условию уравнения.При равенстве суммы модулей 100, или любому числу больше 6, уравнение имеет два решения.
Вывод:
- Если сумма модулей больше расстояния между двумя
точками, то уравнение имеет два решения. - Если сумма модулей равна расстоянию между двумя
точками, то уравнение имеет множество решений, которых принадлежат отрезку
между точками. - Если расстояние между двумя точками меньше
суммы модулей,
то решений нет.
- Если сумма модулей больше расстояния между двумя
4. Закрепление
полученных знаний
- Решите неравенство: |х-5| < 2
Ответ: (3;7) - Решите неравенство: |х+3| ≥ 4
Ответ: x ≤ -7, x ≥ 1 - Решите уравнение: |х-1| +|х+2|=5
Ответ: x=2, x=-3
- Изобразите на координатной плоскости решения
неравенств:1. |х-1|+|х+2|=5
2. | х-1|+|х+2|<5
-
Самостоятельно исследуйте, сколько решений может иметь уравнение в зависимости от значений а:
|х+3| +|х-1|=Ответ:
а) Если, а=4, то уравнение имеет множество решений –
отрезок [-3;1]<ик>
б) Если а>4, то уравнение имеет 2 корня
в) Если а<4, то уравнение не имеет решений
5. Домашнее задание
1. Исследовать уравнение: |х+3| -|х-1|=а
2. Решить № 13, № 16 (а,б)
6. Итог занятия:
- Геометрический смысл модуля
- Как применить геометрический смысл модуля для
решения неравенств - Как применить геометрический смысл модуля для
решения уравнений
Литература
1. Мордкович А.Г. Алгебра ,9 класс, в двух частях,6
издание, Москва, Мнеиозина,2004
2. «Метод
координат», учебное пособие для учащихся, ОЛ ВЗМШ, Москва ,2002
Если (x) — неотрицательное число, то его модуль равен самому числу (x), то есть (|x|=x).
Если (x) — отрицательное число, то его модуль равен противоположному для (x) числу, то есть (|x|=-x).
Получаем:
x=x,если x≥0−x,если x<0
.
Например,
4=4;−4=−(−4)=4;−4.7=−(−4.7)=4.7;7−2=7−2(так как7−2>0).
Геометрический смысл модуля
Геометрическая модель множества действительных чисел
ℝ
— координатная прямая. Точки (a) и (b) на координатной прямой соответствуют действительным числам (a) и (b). Расстояние между точками (a) и (b) обозначим
ρ
((a, b)) (букву
ρ
греческого алфавита читаем «ро»). Это расстояние равно (b — a), если (b > a),
оно равно (a — b), если (a > b), и, наконец,
оно равно нулю, если (a = b).
Для всех трёх случаев справедлива формула:
ρa,b=a−b
.
Пример:
Уравнение задано в аналитическом виде
x−5=3
. С позиции геометрического смысла модуля на координатной прямой необходимо определить точки (x), для которых выполняется условие
ρ(x;5)=3
(точки (x) должны быть удалены от точки (5) на расстояние, равное (3)). Этому условию удовлетворяют точки (2) и (8).
Следовательно, уравнение имеет два корня: (2) и (8).
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.
Видео
Расстояние между точками
Представим числовую ось. Отметим на ней две точки, например 5 и 3. Какое между ними расстояние? Ничего сложного, скажете вы, расстояние равно 5−3=2. И это правильный ответ. Сразу заметим, что 3−5=(−1)(5−3)=−2, то есть при вычитании из меньшей точки большей получаем то же расстояние, но со знаком минус.
Расстояние между точками −2 и −4 равно −2−(−4)=2. И опять, если мы поменяем местами числа в разности, то получим отрицательное расстояние −4−(−2)=(−1)(−2−(−4))=−2
Общий посыл вы уловили. Для нахождения расстояния между двумя точками, надо из большей точки вычесть меньшую. Если сделать наоборот, то получим противоположное, отрицательное расстояние.
Вроде все ясно. Ну и причем здесь модуль? А вот представим, что у вас нет точных значений. Вам просто дали точки a и b, и попросили найти расстояние между ними. Какая-то из двух разностей ниже будет расстоянием:
a−bb−a
Но какая именно? Тут к нам и приходит на помощь модуль. Расстояние между a и b обозначим так:
∣a−b∣
Если a>b, то мы угадали с разностью и получим положительный результат. Взятие модуля никак на него не повлияет. Если a<b, то мы не угадали и получаем отрицательное расстояние. Но, по определению модуля, в результате все-равно получим положительное расстояние.
О
Расстоянием между двумя точками a и b на числовой оси называется модуль их разности: ∣ a − b ∣ .
Наконец, поговорим о модулях одного числа, например ∣5∣ или ∣−2∣. Их можно представить вот так:
∣5∣=∣5−∣∣−2∣=∣−2−∣
В этом смысле модуль одного числа можно понимать как расстояние от до этого числа (до 5 и до −2) на числовой оси.
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение: из рисунка видно, что график симметричен относительно оси Y.
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Докажитесвойствомодуля: ( left
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft( x right) right|=gleft( x right)$ или даже более простому $left| fleft( x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft( x right) right|=left| gleft( x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft( x right) right|=left| gleft( x right) right|Rightarrow fleft( x right)=pm gleft( x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left( 2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; \& 2x+3=-left( 2x-7 right)Rightarrow 2x+3=-2x+7. \end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
[2x+3=-2x+7Rightarrow 4x=4Rightarrow x=1]
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft( x right) right|=left| gleft( x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left( x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
[x-1=pm left( {{x}^{2}}-3x+2 right)]
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; \& {{x}^{2}}-3x+2=-left( x-1 right)Rightarrow {{x}^{2}}-2x+1=0. \end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left( x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:
[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; \& left| x-1 right|=left| left( x-1 right)left( x-2 right) right|. \end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; \& left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; \& left| x-1 right|cdot left( 1-left| x-2 right| right)=0. \end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, \& left| x-2 right|=1. \end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; \& 0,004+0,0001=0,0041 gt 0; \& 5+0=5 gt 0. \end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, \& left| {{x}^{2}}+x-2 right|=0. \end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[x-{{x}^{3}}=0Rightarrow xleft( 1-{{x}^{2}} right)=0Rightarrow left[ begin{align}& x=0 \& x=pm 1 \end{align} right.]
[{{x}^{2}}+x-2=0Rightarrow left( x+2 right)left( x-1 right)=0Rightarrow left[ begin{align}& x=-2 \& x=1 \end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Теги
Геометрическая интерпетация при решении уравнений, содержащих знак модуля
презентация к уроку по алгебре (10 класс) на тему
Материал данного урока содержит «нестандартный» метод, который позволяет более эффективно решать уравнения, содержащие модуль, и, безусловно, может использоваться учителем как на уроках математики в 8-10 классах, так и на факультативных и дополнительных занятиях
Скачать:
| Вложение | Размер |
|---|---|
| geometricheskaya_interpretaciya_pri_reshenii_uravneniy_soderzhashchih_znak_modulya.pptx | 340.74 КБ |
Предварительный просмотр:
Подписи к слайдам:
Тема урока: Геометрическая интерпретация при решении уравнений, содержащих знак модуля МОУ « Осташевская средняя общеобразовательная школа», учитель математики Качайкина Н.Б.
Основные понятия Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А( а ) . Модуль числа 5 равен 5. Пишут: |5| = 5. Число 6 называют модулем числа -6 . Пишут: |-6| = 6. Модуль числа не может быть отрицательным. Противоположные числа имеют равные модули: | -а | = | а |
Расстояние между двумя точками На координатной прямой точка с большей координатой лежит правее точки с меньшей координатой. Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. ВС = 5 – 1 = 4; АС = 5 – (- 2 ) = 7; AD = — 2 – (- 4) = 2 0 -4 — 2 5 1 D A B C
М о д у л ь и расстояние между двумя точками 8 -4 3 -9 -3 5 CD = — 4 – 5 = 5 – (- 4 ) = 9 AB = 3 – 8 = 8 – 3 = 5 MN = — 9 – (- 3 ) = — 3 – (- 9 ) = 6 M N C D A B Формула расстояния между двумя точками координатной прямой с координатами х и а : ρ ( x,a ) = |x — a|
Решите уравнения: | х-2 | = 3, | 3х+6| = 4, | х-3 | + | х-1 | = 5, | х+4| + | х-5| = 9, | 2х-3| + | 2х+3| = 6, | х+5| — | х-8 | = 13, | х+4| — | х-3 | = 1, | 3х-8| — | 3х-2| = 6. | х+7| = | х-5 |
П р о в е р ь с е б я Сколько решений может иметь уравнение | х-4 | = а, в зависимости от значений а ? Сколько решений может иметь уравнение | х+3 | +| х-1 | = а, в зависимости от значений а ? Сколько решений может иметь уравнение | х+3 | -| х-1 | = а, при положительных значениях а ?
Число решений уравнения вида: Ι х – a Ι + Ι х – в Ι = с Если сумма модулей с больше расстояния между двумя точками а и в , то уравнение имеет два решения. Если сумма модулей равна расстоянию между двумя точками, то уравнение имеет множество решений , которые принадлежат отрезку между точками [ a ; в ] . Если расстояние между двумя точками меньше суммы модулей , то решений нет.
Домашняя работа Исследовать уравнения и определить число корней в зависимости от значения а : | х – 4 | — | х +2 | = а, | х+1 | — | х — 6 | = а, | х – 3 | — | х — 8 | = а. С п а с и б о за в н и м а н и е.
П р о в е р ь с е б я Сколько решений может иметь уравнение | х-4 | = а, в зависимости от значений а ? Ответ: а) Если а=0 , то уравнение имеет одно решение; б) Если а >0 , то уравнение имеет 2 корня, в) Если а 4 , то уравнение имеет 2 корня, в) Если а 4 , то уравнение не имеет решений.
Решение уравнения |х — 2|=3 Решить уравнение : х – 2 = 3, значит найти на координатной прямой такие точки х , которые удовлетворяют условию ρ ( х;2 )= 3 ; другими словами удалены от точки с координатой 2 на расстояние 3. Ответ: -1 ; 5. -1 х 5 х 2 х 3 3
| х — 3 | = ρ ( x , 3) ; | х — 1 | = ρ ( x , 1) Нужно найти такую точку Х( х ), что : ρ ( x , 3 ) + ρ ( x , 1 ) = 5. ρ (3, 1) = 2, 2 ρ ( х ; ρ ( х ; -5) — ρ ( х ; = 13 это множество точек координатной прямой, расположенных правее числа 8. Ответ : х [ 8; + ∞) ρ ( х ; -5) ρ ( х ; //////////////////////////// -5 8 х 13
Решение уравнения | х+4 | — | х-3 | = 1 ρ ( x , -4 ) — ρ ( x , 3 ) = 1, где ρ ( x , -4 ) > ρ ( x , 3 ) ρ (-4, 3) = 7, 7 > 1 , следовательно, точка с координатой х находиться внутри отрезка [ -4; 3 ] и такая точа одна. -3 Ответ: 0 -4 3 х ρ ( х ; -4) 0 ρ ( х ; 3)
Решение уравнения |3х-8| — |3х-2| = 6 ρ (8; 2) = 6 , ρ (3х; > ρ (3х; 2) ρ (3х; — ρ (3х; 2) = 6 это множество точек координатной прямой, расположенных левее числа 6. ρ (3х; 3х Мне нравится
Геометрический способ решения уравнений и неравенств с модулем, 9-й класс
Разделы: Математика
Класс: 9
Цель: рассмотреть геометрическое определение модуля. Уметь применять его для решения уравнений и неравенств с модулем, развивать умение исследовать уравнения с параметрами.
1. Организационная часть (Цель занятия)
2. Актуализация знаний
-
Алгебраическое определение модуля
|a| =
Способы решения уравнений содержащих модуль
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Способы решения уравнений содержащих модуль.
1. Основные способы, используемые при решении уравнений, содержащих модуль.
Напомним основные понятия, используемые в данной теме.
Уравнением с одной переменной называют равенство, содержащее переменную.
Корнями уравнения называются значения переменной, при которых уравнение обращается в верное равенство.
Решить уравнение – значит, найти все его корни или доказать, что корней нет.
Уравнением с модулем называют равенство, содержащее переменную под знаком модуля.
При решении уравнений, содержащих знак абсолютной величины, мы будем основываться на определении модуля числа и свойствах абсолютной величины числа.
Свойства модуля
Существует несколько способов решения уравнений с модулем. Рассмотрим каждый из них.
1 СПОСОБ. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО РАСКРЫТИЯ МОДУЛЯ.
Пример 1. Решим уравнение |х-5|=4.
Исходя из определения модуля, произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-5≥0, то уравнение примет вид х-5=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-5)=4 или х-5= -4. Решая полученные уравнения, находим: х1=9, х2=1.
Ответ: 9; 1.
Решим этим же способом уравнение, содержащее «модуль в модуле».
Пример 2. Решим уравнение ||2х-1|-4|=6.
Рассуждая аналогично, рассмотрим два случая.
1). |2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо 2х-1= -10. Откуда х1=5,5, х2= -4,5.
2). |2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен.
Ответ: 5,5; -4,5.
2 СПОСОБ. МЕТОД ИНТЕРВАЛОВ.
Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ.
Пример 3. Решим уравнение |х+3|+|х-1|=6.
Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка:
-3 1
Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке (х
Пример 4. |2-х|=2х+1.
Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток [-½; +∞). Найдем нуль выражения, стоящего под знаком модуля: 2-х=0, х=2.
В первом промежутке: 2-х=2х+1, х=⅓. Это значение принадлежит ОДЗ, значит, является корнем уравнения.
Во втором промежутке: -2+х=2х+1, х= -3. -3 не принадлежит ОДЗ, а следовательно не является корнем уравнения. Ответ: ⅓.
3 СПОСОБ. ГРАФИЧЕСКИЙ МЕТОД.
Суть данного метода заключается в использовании графиков функций для нахождения корней уравнения. Этот метод реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.
Преобразуем уравнение: 1 + |x| = 0.5
Графиком функции 
являются лучи — биссектрисы 1-го и 2-го координатных углов. Графиком функции 
является прямая, параллельная оси OX и проходящая через точку -0,5 на оси OY.
Графики не пересекаются, значит, уравнение не имеет решений.
Ответ: нет решений.
Пример 5. |х+1|=2. Построим графики функций у=|х+1| и у=2.
Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ. Абсциссы точек пересечения графиков и есть корни уравнения: х 1 =1, х 2 = -3. Ответ: 1; -3.
Пример 6. |х 2 -1|=|4-х 2 |.
Построим графики функций у=|х 2 -1| и у=|4-х 2 |. Для этого построим графики функций у= х 2 -1 и у=4-х 2 , а затем отобразим часть графиков, лежащую ниже оси ОХ.
х 1 ≈1,6; х 2 ≈-1,6.
4 СПОСОБ. МЕТОД РЕШЕНИЯ ПРИ ПОМОЩИ ЗАВИСИМОСТЕЙ МЕЖДУ ЧИСЛАМИ А И В, ИХ МОДУЛЯМИ И КВАДРАТАМИ ЭТИХ ЧИСЕЛ.
| а |=| в | 
а=в или а=-в;
а 2 =в 2 а=в или а=-в; (1)
| а |=| в | а 2 =в 2 (2)
Пример 7 . Решим уравнение |х 2 -8х+5|=|х 2 -5|.
Учитывая соотношение (1), получим:
х 2 -8х+5= х 2 -5 или х 2 -8х+5= -х 2 +5
Таким образом, корни исходного уравнения: х 1 =1,25; х 2 =0; х 3 =4.
В силу соотношения (2) получаем: (х+3) 2 =(х-5) 2 ;
х 2 +6х+9= х 2 -10х+25;
Пример 9 . (1-3х) 2 =(х-2) 2 .
Учитывая соотношение (2), получаем: |1-3х|=|х-2|, откуда из соотношения (1), имеем:
1-3х=х-2 или 1-3х= -х+2
5 СПОСОБ. ИСПОЛЬЗОВАНИЕ ГЕОМЕТРИЧЕСКОЙ ИНТЕРПРЕТАЦИИ МОДУЛЯ.
Опорная информация: геометрический смысл модуля разности величин – это расстояние между ними. Например, геометрический смысл выражения |х-а| — длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.
Исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой х до двух фиксированных точек с абсциссами 2 и 3. Тогда очевидно, что все точки с абсциссами, принадлежащими отрезку [2;3] обладают требуемым свойством, а точки, расположенные вне этого отрезка – нет. Отсюда, множеством решений уравнения является отрезок [2;3].
Рассуждая аналогично, получим, что разность расстояний до точек с абсциссами 2 и 3 равна 1 только для точек, расположенных на координатной оси правее числа 3. Следовательно, решением данного уравнения будет являться луч, выходящий из точки 3, и направленный в положительном направлении оси ОХ.
Обобщением вышеприведенных уравнений 10 и 11 являются следующие равносильные переходы:
|х-а|+|х-в|=в-а, где в ≥ а а ≤ х ≤ в
|х-а|-|х-в|=в-а, где в ≥ а х ≥ в
Проанализировав представленные способы решения уравнений, содержащих модуль, можно сделать вывод, что ни один из них не является универсальным и для получения наилучших результатов необходимо добиваться того, чтобы ученик овладел возможно большим количеством методов решения, оставляя право выбора решения за собой.
Решим аналитически и графически уравнение |x — 2| = 3.
А) Аналитическое решение
Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем
неотрицательно, т. е. x — 2 
0, тогда оно «выйдет» из под знака модуля со знаком «плюс» и уравнение примет вид: x — 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: 
или x — 2=-3
Таким образом, получаем, либо x — 2 = 3, либо x — 2 = -3. Решая полученные уравнения, находим: 
Ответ:
Теперь можно сделать вывод: если модуль некоторого выражения равен действительному положительному числу a, тогда выражение под модулем равно либо a, либо 
.
Одним из способов решения уравнений, содержащих модуль, является графический способ. Суть этого способа заключается в том, чтобы построить графики данных функций. В случае, если графики пересекутся, точки пересечений данных графиков будут являться корнями нашего уравнения. В случае, если графики не пересекутся, мы сможем сделать вывод, что уравнение корней не имеет. Этот способ, вероятно, реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.
Другой способ решения уравнений, содержащих модуль — это способ разбиения числовой прямой на промежутки. В этом случае нам нужно разбить числовую прямую так, что по определению модуля, знак абсолютной величины на данных промежутках можно будет снять. Затем, для каждого из промежутков мы должны будем решить данное уравнение и сделать вывод, относительно получившихся корней (удовлетворяют они нашему промежутку или нет). Корни, удовлетворяющие промежутки и дадут окончательный ответ.
Установим, при каких значениях x, модуль равен нулю: 
Получим два промежутка, на каждом из которых решим уравнение:
Получим две смешанных системы:
(1) 
(2) 
Решим каждую систему:
(1) 
(удовлетворяет данному промежутку)
(2) 
Ответ: 
Для решения уравнения графическим способом, надо построить графики функций 
и 
Для построения графика функции , построим график функции 
— это прямая, пересекающая ось OX в точке (2; 0), а ось OY в точке 
а затем часть прямой, лежащую ниже оси OX зеркально отразить в оси OX.
Графиком функции 
является прямая, параллельная оси OX и проходящая через точку (0; 3) на оси OY.
Абсциссы точек пересечения графиков функций дадут решения уравнения.
Прямая графика функции y=3 пересеклась с графиком функции y=|x – 2| в точках с координатами (-1; 3) и (5; 3), следовательно, решениями уравнения будут абсциссы точек:
Ответ:
Практика обучения учащихся способам решения уравнений, содержащих модули, позволила выявить достоинства и недостатки каждого способа, которые для удобства сведены в таблицу.
Метод последовательного раскрытия модулей
1). Объявляя условие раскрытия одного модуля, можно пользоваться им для раскрытия других модуле тем самым, выигрывая время в решении задачи.
2). Последовательность действий, направленных на поиск ответа, позволяет контролировать и проверять промежуточные результаты.
Необходимость раскрытия модуля, что для некоторых заданий приводит к потере темпа в получении ответа.
Самый эффективный способ, так как сопровождается относительно небольшим объемом работы.
В силу необходимости нахождения концов интервалов может возникнуть ситуация, когда соответствующее уравнение либо вызывает серьезные затруднения при определении корней, либо недоступно ученику на данном этапе обучения.
Данный способ имеет очень широкое применение в других темах школьного курса математики.
Ответ определяется приблизительно.
Метод решения при помощи зависимостей между числами, их модулями и квадратами этих чисел
В некоторых случаях применение данного способа позволяет решать уравнения определенного вида на более раннем этапе.
В некоторых случаях выбор данного способа приводит к громоздкому решению, а иногда решение сводится к уравнению, недоступному для ученика на данном этапе обучения.
Геометрическая интерпретация модуля
Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.
Применение данного способа ограничивается уравнениями определенного вида.
Проанализировав достоинства и недостатки каждого из указанных способов, можно с уверенностью сказать, что на мотивационном этапе формирования умения решать уравнения с модулем ученикам следует показывать все, доступные на данном этапе обучения способы решения, и, главное, на конкретных примерах доказывать, что первый этап решения – выбор самого эффективного способа.
Рассмотрим пример |(х-1)(х-3)|=х-3.
Это уравнение можно решить тремя способами.
а) последовательное раскрытие модуля:
Если (х-1)(х-3) ≥ 0, то Если (х-1)(х-3) 2 -4х+3=х-3, х 2 -4х+3= -х+3,
х 2 -5х+6=0, х 2 -3х=0,
х 1 =3, х 2 =2. х 1 =0, х 2 =3.
2 – не удовлетворяет условию. 0, 3 — не удовлетворяет условию.
Ответ: 3.
б) метод интервалов: найдем концы интервалов, решив уравнение (х-1)(х-3)=0, откуда х 1 =1, х 2 =3.
(х-1)(х-3)=х-3, -(х-1)(х-3)=х-3, (х-1)(х-3)=х-3,
х 1 =2, х 2 =3. х 1 =0, х 2 =3. х 1 =2, х 2 =3.
2 (-∞; 1), 0 [1; 3). 2 [3; +∞).
3 (-∞; 1).
Ответ: 3.
в) графический метод: для решения уравнения построим в одной системе координат графики функций у=|х 2 -4х+3| и у=-3.
Построим у=|х 2 -4х+3|. Для этого сначала рассмотрим функцию у=х 2 -4х+3, графиком которой является парабола, ветви направлены вверх. Вершина параболы в точке (2; -1). Строим график и отображаем часть параболы, которая лежит ниже оси ОХ в верхнюю полуплоскость. Далее в этой же системе координат строим график у=х-3. Графики функций пересеклись в точке с абсциссой 3.
Ответ: 3.
Таким образом, можно сделать следующий вывод: систематическое использование различных способов для решения уравнений, содержащих абсолютную величину, приводит не только к повышению интереса к математике, повышению творческой активности школьников, но и повышает уверенность детей в собственных силах, так как у них имеется возможность выбора того способа решения, который наиболее эффективен в каждом конкретном случае.
ТЕСТОВЫЕ ЗАДАНИЯ по теме «Решение уравнений с модулем».
1. Какие числа являются решениями уравнения |х+3|= -4?
а) -7; б) -7; 1; в) нет корней; г) 1.
2. Решите уравнение |х+3|=7:
а) 7; б) -7; в) 0; 7; г) 7; -7.
3. Определите координаты точки пересечения графиков функций у=|2х+1| и у=0:
а) (0;0); б) (-0,5;0); в) (0;-0,5); г) (0,5;0).
4. Решите уравнение |х+3|+|х-1|=6:
а) 3; -2; б) 4; -2; в) -4; 2; г) 2; -3.
5. Сколько точек пересечения имеют графики функций у=||5,5х-4|+2| и у=3?
а) 1; б) 2; в) 3; г) 4.
6. Решите уравнение |3х-7|=1-х:
а) 2; 3; б) -2; 3; в) -3; 2; г) -2; -3.
7. Сколько решений имеет уравнение (2,5х-5)2=(0,5х-6)2:
а) 1; б) 2; в) 3; г) 4.
СИСТЕМА КАРТОЧЕК-ЗАДАНИЙ по теме «Решение уравнений с модулем».
1. ЗАДАНИЯ С УКАЗАНИЯМИ ИЛИ АЛГОРИТМИЧЕСКИМИ ПРЕДПИСАНИЯМИ И ОБРАЗОМ ВЫПОЛНЕНИЯ.
УКАЗАНИЯ ОБРАЗЕЦ ЗАДАНИЕ
Если |х-а|+|х-в|=в-а, где в ≥ а, то
а ≤ х ≤ в
|х-1|+|х-2|=1,
1 ≤ х ≤ 2.
Ответ: [1; 2]
а) |х-4|+|х-5|=1,
б) |х|-|х-1|=1,
в) |х-6|+|х-8|=2,
г) |х-0,5|-|х-4,5|=4.
Если |х-а|-|х-в|=в-а, где в ≥ а, то
х ≥ в
|х-1|-|х-2|=1,
х ≥ 2.
Ответ: [2; +∞).
АЛГОРИТМ ОБРАЗЕЦ ЗАДАНИЯ
1. Отметить все нули подмодульных выражений на числовой прямой. Они разобьют числовую прямую на промежутки, в которых все подмодульные выражения имеют постоянный знак.
2. Из каждого промежутка взять произвольное число и подсчетом определить знак подмодульного выражения, по знаку раскрыть модули.
3. Решить уравнения и выбрать решения, принадлежащие данному промежутку. |х+1|+|х+2|=1.
Решение.
Подмодульные выражения х+1 и х+2 обращаются в нуль при х= -1, х= -2.
1) -3 (-∞; -2]
-х-1-х-2=1; х= -2;
-2 (-∞; -2].
2) -1,5 (-2; -1)
-х-1+х+2=1; 1=1; х — любое число из промежутка (-2; -1).
3) 0 [-1; +∞)
х+1+х+2=1; х= -1;
-1 [-1; +∞).
Ответ: [-2; -1].
1) |14-х|+|х+1|=7;
2) |х|-|х+2|=2;
3) |х2-4|=|2х-1|;
4) | х2-6х+5|+|3-х|=3
2. ЗАДАНИЯ «НАЙДИ ОШИБКУ».
1.
Решить уравнение: |х2-8х+5|=| х2-5|.
Решение.
|х2-8х+5|=| х2-5|
х2-8х+5= х2-5, или х2-8х+5=5- х2,
-8х+10=0, 2 х2-8х=0,
х=1,25. х(2х-8)=0,
х=0, или 2х-8=0,
2х=8,
х=0,25.
Ответ: 1,25; 0,25. ВЕРНОЕ РЕШЕНИЕ
2.
Решить уравнение х2-6х+|х-4|+8=0.
Решение.
Если х-4 ≥ 0, то Если х-4 Решить уравнение |х-1|-2|х+3|+х+7=0.
Решение.
Решим уравнение методом интервалов, для этого найдем концы интервалов, решив уравнения
х-1=0 и х+3=0
х=1 х= -3.
-х+1-2(-х-3)+х+7=0; -х+1-2х-6+х+7=0; х-1-2х-6+х+7=0;
2х+14=0; -2х+2=0; 0=0.
х= -7. х=1. х — любое число.
Ответ: х – любое число. ВЕРНОЕ РЕШЕНИЕ
3. ЗАДАНИЯ С СОПУТСТВУЮЩИМИ УКАЗАНИЯМИ И ИНСТРУКЦИЯМИ.
1.
Решить уравнение |х-2|+|2х-7|=3.
Решение.
Решим уравнение методом интервалов.
1) Найдите нули подмодульных выражений, решив уравнения:
х-2=0 и 2х-7=0.
х1=… х2=…
2) Отметьте полученные значения на координатном луче.
3) Решите исходное уравнение на каждом из интервалов, предварительно определив знак подмодульного выражения. Учитывая знак, раскрыть модули.
4) Проверьте, принадлежат ли найденные корни указанным промежуткам.
Ответ: …………………………………………………….
2.
Решить уравнение ||х-3|-х+1|=6.
Решение.
1) Раскройте внешний модуль, используя определение: |а|=а, если а ≥ 0 и
|а|= -а, если а 4. ЗАДАНИЯ С ПРИМЕНЕНИЕМ КЛАССИФИКАЦИИ.
1.
Выпишите уравнения, которые решаются с помощью зависимостей между величинами, их модулями и квадратами величин. Решите эти уравнения.
1) ||х|+3|=3;
2) |х|+|х+4|=х-1;
3) |х+2|=|3-х|;
4) |х+3|+|х-1|=7;
5) (2х-3)2=(3,5х-1)2;
6) |х2-4х+5|=|х2-9|;
7) |11х-7|= -3;
|х-2|+|х-1|=1;
9) х2-х-2=|5х-3|;
2.
Выпишите уравнения, которые решаются с использованием геометрической интерпретации модуля. Решите эти уравнения.
1) |х|-|х-8|=2;
2) |х 2 -2х-3|=3х-3;
3) |2х-|2х-|2х-3|||=0;
4) |х-1|-2|х+4|+х+11=0;
5) |х-3|+|х-4|=1;
6) (5х-4) 2 =(2х-1) 2 ;
7) |2,5х-11|= -2;
|х-7|-|х-9|=2.
5. ЗАДАНИЯ С ВЫПОЛНЕНИЕМ НЕКОТОРОЙ ЧАСТИ.
1.
Решить уравнение (х 2 -5х+6)2-5•| х 2 -5х+6|+6=0.
Решение.
Пусть | х 2 -5х+6|=t, тогда, учитывая, что (х 2 -5х+6)2=| х 2 -5х+6|2, получим уравнение: t 2 -5t+6=0. Решением этого уравнения являются числа ……. поэтому исходное уравнение равносильно совокупности двух уравнений:
| х 2 -5х+6|=… или | х 2 -5х+6|=…
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
ПРОВЕРОЧНАЯ РАБОТА по теме «Решение уравнений с модулем»
1. Решите уравнение |х-3|=7.
2. Решите графически уравнение |2х+1|=3.
3. Решите уравнение методом интервалов |х+1|+|х-1|=3.
4. Решите уравнение методом последовательного раскрытия модулей |-х+2|=2х+1.
5. Решите уравнение (2х+3) 2 =(х-1) 2 .
6. Решите уравнение самым удобным способом |х 2 +6х+2|=3|х+2|.
7. При каком значении а уравнение можно решить, используя геометрическую интерпретацию модуля: |х-а|+|х-9|=1?
http://urok.1sept.ru/articles/519192
http://infourok.ru/sposobi-resheniya-uravneniy-soderzhaschih-modul-398462.html