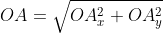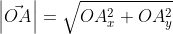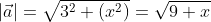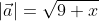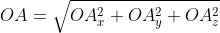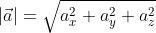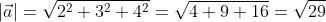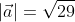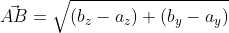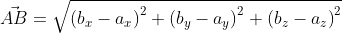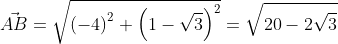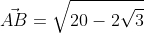Abs — функция языка Паскаль, которая вычисляет модуль числа.
Sqr — функция языка Паcкаль, которая возводит число в квадрат.
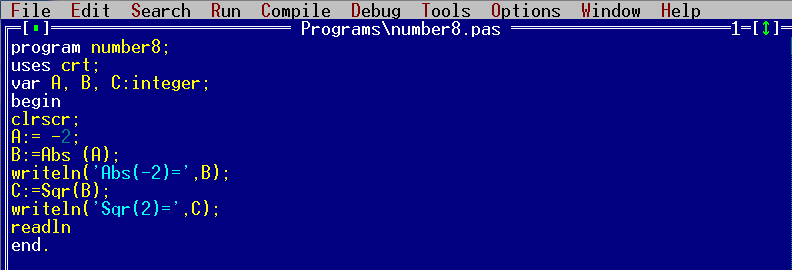
program number8;
uses crt;
var A, B, C:integer;
begin
clrscr;
A:= -2;
B:=Abs (A);
writeln('Abs(-2)=',B);
C:=Sqr(B);
writeln('Sqr(2)=',C);
readln
end.
Строка №7. Функция Abs вычисляет модуль числа, стоящего в скобках после функции. В данном случае вычисляется модуль переменной «A», которая имеет значение «-2». Так как модуль «|-2|» равен «2», то «2» и будет результатом операции Abs.
Строка №9. Функция Sqr возводит число, стоящее в скобках в квадрат. В данном случае в квадрат возводится переменная «B», т.е. число «2». Таким образом, результатом операции будет число «4».
Дополнение к материалу.
В примерах №6, 7, 8 мы использовали небольшие числа (-2, 3, 17 и т.д.). Для всех переменных, в которые эти числа записывались, мы указывали тип данных INTEGER. Следует сказать, что данный тип данных используется не для всех чисел, а только для целых, лежащих в диапазоне от – 32768 до 32767. И если мы будем использовать в наше программе числа, которые лежат вне этих пределов (например – 32987 или 36789), то мы должны использовать другой тип данных.
Диапазон значений для различных типов данных можно посмотреть в таблице.
| Тип данных | Запись | Длина в байтах |
|---|---|---|
| integer | -32 768….32 767 | 2 |
| byte | 0…255 | 1 |
| word | 0…65 535 | 2 |
| shortint | -128….127 | 1 |
| longint | -2 147 483 648….2 147 483 647 | 4 |
Использование различных типов данных обусловлено тем, что для каждого из них выделяется определенное количество ячеек в памяти компьютера. Если мы используем в программе числа от 0 до 255, то наиболее целесообразно будет использовать тип данных BYTE. Хотя можно использовать и любой другой тип данных. Например, для числа 10 можно использовать и BYTE и LONGINT, но тогда в первом случае будет расходоваться 1 байт в памяти компьютера, а во втором — целых 4 байта. Учитывая то, что программа должна расходовать как можно меньше памяти, рационально будет использовать для данного примера тип данных BYTE.
Онлайн калькулятор. Модуль вектора. Длина вектора
Этот онлайн калькулятор позволит вам очень просто найти длину вектора для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление модуля вектора и закрепить пройденный материал.
Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам

Форма представления вектора:
Инструкция использования калькулятора для вычисления длины вектора
Ввод даных в калькулятор для вычисления длины вектора (модуля вектора)
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел..
Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Вычисления длины вектора (модуля вектора)
Например, для вектора a = x; ay; az> длина вектора вычисляется cледующим образом:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Нахождение длины вектора, примеры и решения
Длина вектора — основные формулы
Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.
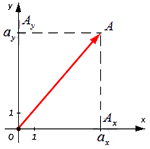
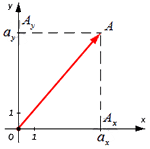
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .
Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .
Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .
Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.
Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.
Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e
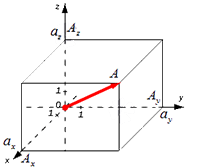
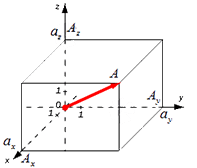
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)
В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .
Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .
Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.
Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( — 3 ) 2 + 5 2 = 5 2 .
Длина вектора через координаты точек его начала и конца
Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.
Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x — a x ; b y — a y ) значит, его длина может быть определена по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2
А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле
A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2
Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x — a x ) 2 + ( b y — a y ) 2 : A B → = ( — 3 — 1 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 .
Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( — 3 — 1 ; 1 — 3 ) = ( — 4 ; 1 — 3 ) ; A B → = ( — 4 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 . —
Ответ: A B → = 20 — 2 3 .
Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .
Для начала распишем длину вектора A B → по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 = ( 5 — 0 ) 2 + ( 2 — 1 ) 2 + ( λ 2 — 2 ) 2 = 26 + ( λ 2 — 2 ) 2
Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :
26 + ( λ 2 — 2 ) 2 = 30 26 + ( λ 2 — 2 ) 2 = 30 ( λ 2 — 2 ) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .
Нахождение длины вектора по теореме косинусов
Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.
Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.
Рассмотрим такой случай на следующем примере.
Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .
Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .
Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x — a x ) 2 + ( b y — a y ) 2 или A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 , в некоторых случаях следует использовать теорему косинусов.
Длина вектора — основные формулы
Время чтения: 16 минут
Основные понятия вектора
Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.
Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
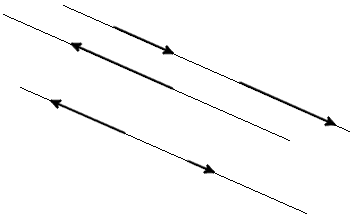
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать 
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор 

На взятой системе координат, от её начала отложим вектор
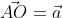
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
Когда вектор 
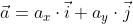


Чтобы рассчитать длину 
Чтобы найти модуль вектора используем ранее приведённую формулу
Ответ:
Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор 

В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому
из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA

Ответ:
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор 
При этом формула вычисления длины вектора 
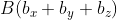
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
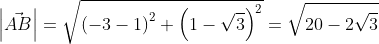
Существует второй вариант решения, где формулы применяются по очереди:
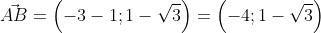
Ответ:
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))
В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).
В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)
Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.
длина вектора формула для трёхмерного пространства;
длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.
Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.
http://zaochnik.com/spravochnik/matematika/vektory/dlina_vectora/
http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html
Python предоставляет пакет Abstract Base Class (ABC) для облегчения реализации абстрактных классов, и по понятным причинам этот модуль называется abc. Абстрактные классы позволяют разработчикам создавать схемы для подклассов, чтобы они имели определенное поведение, поэтому давайте посмотрим, как мы это делаем на примере использования из обычного сценария обработки данных…
Фоновый контекст
Учтите, что мы пишем код для разработки преобразователя формата данных в формат клиента по вашему выбору для вашей системы приема машинного обучения. Поскольку системы данных — это живые организмы, и их внутренняя химия постоянно меняется, и существует множество доступных форматов данных, лучше всего подходить к этой проблеме объектно-ориентированным способом. Итак, давайте создадим класс для нашего преобразователя.
Как упоминалось ранее, две основные проблемы проектирования, с которыми мы сталкиваемся — это несколько форматов данных и возможные изменения во входных данных. Таким образом, чтобы справиться с проблемами, мы хотели бы, чтобы базовый класс, который предоставляет проект, мог бы иметь функциональность в наших различных подклассах преобразователей.
Теперь давайте создадим абстрактный класс для определения схемы нашего базового преобразователя. Имя моего пользовательского формата будет Naruto.
class NarutoConverter():
def convert(self): pass
def clean_string(self): pass
class JSONtoNaruto(NarutoConverter):
def __init__(self, input_file):
self.__input = input_file
Наш преобразователь имеет два метода convert для преобразования входного формата в формат Naruto и метод clean_string для работы с различным качеством входных строк.
Теперь, поскольку мы создаем абстрактный класс, мы не хотим, чтобы кто-либо создавал экземпляры этого класса, поскольку это всего лишь черновик для будущих преобразователей. Однако то, как мы создаем класс выше, не препятствует созданию экземпляра этого класса.
Вторая проблема с приведенным выше кодом заключается в том, что он не требует, чтобы подклассы реализовывали функциональность методов convert и clean_string. В этом случае приведенный выше код в JSONtoNaruto не выдаст ошибку, даже если методы не реализованы. Давайте посмотрим, как мы можем решить эти проблемы в следующем разделе.
Модуль abc
Теперь давайте посмотрим, как объявить библиотеку NarutoConverter с abc и достичь нашей цели.
from abc import ABC, abstractmethod
class NarutoConverter(ABC):
@abstractmethod
def convert(self): pass
@abstractmethod
def clean_string(self): pass
Основной рецепт включает в себя создание абстрактного класса как подкласса ABC из модуля abc и использование декоратора @abstractmethod перед каждым объявлением абстрактного метода. Это помогает применить функциональность абстрактного класса к вашему пользовательскому подклассу. Теперь, если мы попытаемся создать экземпляр класса NarutoConverter, это вызовет исключение и предотвратит создание экземпляра этого абстрактного класса. Теперь давайте посмотрим на реализацию подкласса JSONtoNaruto.
class JSONtoNaruto(NarutoConverter):
def __init__(self, input_file):
self.__input = input_file
def convert(self):
naruto_file = self.__input
return naruto_file
def clean_string(self):
clean_str = self.__input.str
return clean_str
В приведенном выше коде мы реализовали оба метода. Если мы запустим код без реализации какого-либо из методов, python вызовет одну из следующих ошибок. Это поведение обеспечивается с помощью декоратора @abstractmethod, который предотвращает создание экземпляра класса без реализации метода.
TypeError: Can't instantiate abstract class JSONtoNaruto with abstract methods convert
TypeError: Can't instantiate abstract class JSONtoNaruto with abstract methods clean_string
Модуль (или абсолютная величина) – это неотрицательное значение любого числа. То есть, например, для отрицательного числа -32 он равняется 32, в то время, как для любого положительного числа равен этому же числу.
Давайте посмотрим, как найти модуль числа в Эксель.
Использование функции ABS
В программе Excel для нахождения модуля числа предусмотрена специальная функция ABS, формула которой в общем виде может выглядеть так:
- ABS(число)
- ABS(адрес_ячейки_с_числом)
Допустим, нам нужно найти модуль числа -27. Для этого в любой свободной ячейке пишем выражение: =ABS(-27).
Нажав клавишу Enter получаем результат в выбранной ячейке.
Некоторые пользователи по привычке пишут в ячейке математическое выражение, а именно, |-27|.
В данном случае после нажатия Enter программа выдаст ошибку.
Вместо того, чтобы вручную прописывать формулы, можно использовать Мастер функций.
- Выбрав ячейку, куда мы планируем добавить функцию и провести расчеты, кликаем по кнопке “Вставить функцию” (fx) слева от строки формул.
- В открывшемся окне вставки функций выбираем категорию “Математические”, в предложенном списке кликаем по оператору “ABS” и жмем OK.
- На экране отобразится окно для заполнения аргумента функции – “Число”. Адрес ячейки с числовыми значением, модуль которого нужно посчитать, можно указать вручную, либо просто кликнуть по ней в самой таблице. Курсор при этом должен находиться в поле для ввода значения аргумента. По готовности жмем кнопку OK.
- В ячейке с функцией появится результат вычислений.
- Если нужно посчитать модули по всему столбцу, можно растянуть формулу на другие строки. Для этого наводим указатель мыши на ячейку с результатом, когда появится небольшой черный плюсик, зажав левую кнопку мыши тянем его вниз до последней ячейки столбца (или до той ячейки, для которой нужно посчитать аналогичный результат).
- Все готово, мы получили модули всех значений в исходном столбце.
Заключение
Таким образом, в Эксель можно легко и быстро посчитать модуль числа с помощью специально предназначенной для этого функции. Причем ввиду того, что формула достаточно проста и содержит всего один аргумент, ее можно сразу писать в ячейке таблицы. Или же можно воспользоваться мастером функций, который позволит безошибочно выполнить расчет.
Встроенная функция abs(x) в Python возвращает абсолютное значение аргумента x, который может быть целым или числом с плавающей точкой, или же объектом, реализующим функцию __abs__(). Для комплексных чисел функция возвращает их величину. Абсолютное значение любого числового значения -x или +x — это всегда соответствующее положительное +x.
| Аргумент | x |
целое число, число с плавающей точкой, комплексное число, объект, реализующий __abs__() |
| Возвращаемое значение |
|x| |
возвращает абсолютное значение входящего аргумента |
Следующий код демонстрирует, как получить абсолютное значение 42 положительного числа 42.
x = 42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Вывод: Абсолютное значение 42 это 42
Вывод: «Абсолютное значение 42 это 42».
То же самое, но уже с отрицательным -42.
x = -42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Вывод: Абсолютное значение -42 это 42
Пример с числом float
Вот как получить абсолютное значение 42.42 и для -42.42:
x = 42.42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Абсолютное значение 42.42 это 42.42
x = -42.42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Абсолютное значение -42.42 это 42.42
Комплексное число
Абсолютное значение комплексного числа (3+10j).
complex_number = (3+10j)
abs_complex_number = abs(complex_number)
print(f"Абсолютное значение {complex_number} это {abs_complex_number}")
# Абсолютное значение (3+10j) это 10.44030650891055
abs() vs fabs()
abs(x) вычисляет абсолютное значение аргумента x. По аналогии функция fabs(x) модуля math вычисляет то же значение. Разница лишь в том, что math.fabs(x) возвращает число с плавающей точкой, а abs(x) вернет целое число, если в качестве аргумента было целое число. Fabs расшифровывается как float absolute value.
Пример c fabs():
x = 42
print(abs(x))
# 42
import math
print(math.fabs(x))
# 42.0
abs() vs. np.abs()
И abs() в Python, и np.abs() в NumPy вычисляют абсолютное значение числа, но есть два отличия. np.abs(x) всегда возвращает число с плавающей точкой. Также np.abs(x) принимает массив NumPy, вычисляя значение для каждого элемента коллекции.
Пример:
x = 42
print(abs(x))
# 42
import numpy as np
print(np.fabs(x))
# 42.0
a = np.array([-1, 2, -4])
print(np.abs(a))
# [1 2 4]
abs и np.abs абсолютно идентичны. Нет разницы какой использовать. У первой преимущество лишь в том, что ее вызов короче.
Вывод
Функция abs() — это встроенная функция, возвращающая абсолютное значение числа. Она принимает целые, с плавающей точкой и комплексные числа на вход.
Если передать в abs() целое число или число с плавающей точкой, то функция вернет не-отрицательное значение n и сохранит тип. Для целого числа — целое число. Для числа с плавающей точкой — число с плавающей точкой.
>>> abs(20)
20
>>> abs(20.0)
20.0
>>> abs(-20.0)
20.0
Комплексные числа состоят из двух частей и могут быть записаны в форме a + bj, где a и b — это или целые числа, или числа с плавающей точкой. Абсолютное значение a + bj вычисляется математически как math.sqrt(a**2 + b**2).
>>> abs(3 + 4j)
5.0
>>> math.sqrt(3**2 + 4**2)
5.0
Таким образом, результат всегда положительный и всегда является числом с плавающей точкой.