Как найти режим сгруппированных данных (с примерами)
17 авг. 2022 г.
читать 2 мин
Часто нам может понадобиться вычислить моду данных, которые каким-то образом сгруппированы.
Напомним, что мода представляет значение, которое встречается чаще всего.
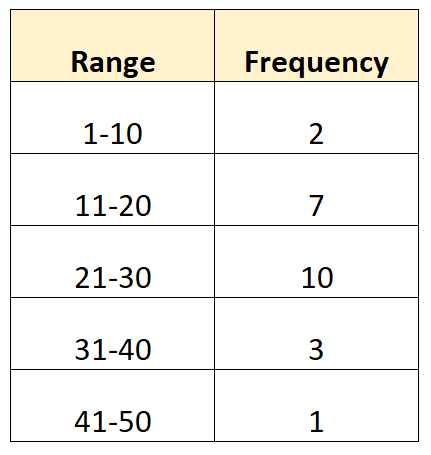
Например, предположим, что у нас есть следующие сгруппированные данные:
Хотя невозможно рассчитать точную моду, поскольку мы не знаем исходных значений данных , можно оценить моду, используя следующую формулу:
Режим сгруппированных данных = L + W[(F m – F 1 )/( (F m -F 1 ) + (F m – F 2 ) )]
куда:
- L : Нижний предел модального класса
- W : ширина модального класса
- F m : Частота модального класса
- F 1 : Частота занятия непосредственно перед модальным занятием.
- F 2 : Частота занятия сразу после модального занятия.
Примечание.Модальный класс — это просто класс с наибольшей частотой. В приведенном выше примере модальный класс будет 21-30, так как он имеет самую высокую частоту.
В следующих примерах показано, как вычислить моду сгруппированных данных в различных сценариях.
Пример 1: Расчет режима сгруппированных данных
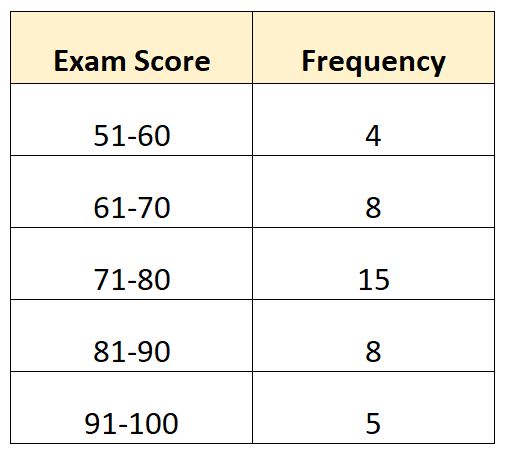
Предположим, у нас есть следующее частотное распределение, показывающее, что экзамен сдан 40 учащимся в определенном классе:
В этом примере модальный класс 71-80.
Зная это, мы можем рассчитать следующие значения:
- L : Нижний предел модального класса: 71
- W : Ширина модального класса: 9
- F m : Частота модального класса: 15
- F 1 : Частота занятия непосредственно перед модальным занятием: 8
- F 2 : Частота занятия сразу после модального занятия: 8
Мы можем подставить эти значения в формулу для расчета режима распределения:
- Мода = L + W[(F m – F 1 )/( (F m -F 1 ) + (F m – F 2 ) )]
- Мода = 71 + 9 [(15-8) / ( (15-8) + (15-8) )]
- Мода = 75,5
По нашим оценкам, модальный экзаменационный балл составляет 75,5 .
Пример 2: Расчет режима сгруппированных данных
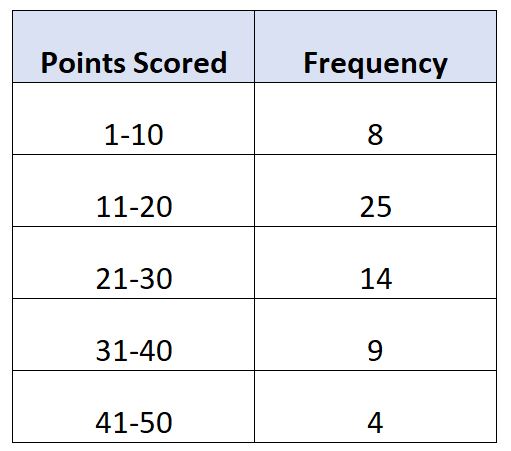
Предположим, у нас есть следующее распределение частот, которое показывает количество очков, набранных за игру 60 баскетболистами:
В этом примере модальный класс 11-20.
Зная это, мы можем рассчитать следующие значения:
- L : Нижний предел модального класса: 11
- W : Ширина модального класса: 9
- F m : Частота модального класса: 25
- F 1 : Частота занятия непосредственно перед модальным занятием: 8
- F 2 : Частота занятия сразу после модального занятия: 14
Мы можем подставить эти значения в формулу для расчета режима распределения:
- Мода = L + W[(F m – F 1 )/( (F m -F 1 ) + (F m – F 2 ) )]
- Мода = 11 + 9 [(25-8) / ( (25-8) + (25-14) )]
- Режим = 16,46
Мы оцениваем, что набранные модальные баллы составляют 16,46 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные операции с сгруппированными данными:
Как найти среднее и стандартное отклонение сгруппированных данных
Как найти медиану сгруппированных данных
Как рассчитать процентильный ранг для сгруппированных данных
Как рассчитать интервал модального класса из видео с таблицей частот
Найти модальный класс из сгруппированной частотной таблицы на самом деле довольно просто. Все, что вам нужно сделать, это найти группу с наибольшей частотой. Это потому, что режим — это число, которое встречается чаще всего. Убедитесь, что вы записываете группу, а не частоту. Если вы сделаете это, вы не получите никаких оценок. На большинстве экзаменов определение модального класса будет приносить только одну оценку, так как нет никаких результатов, которые можно было бы показать. Так что просто не забудьте искать группу с наибольшей частотой.
Давайте рассмотрим несколько примеров, которые включают поиск модального класса из сгруппированной таблицы частот.
Пример 1
В таблице частот показаны веса некоторых пациентов, перенесших операцию у врача. 13 человек имеют вес от 60 кг до 70 кг, 2 человека имеют вес от 70 кг до 75 кг, 45 человек имеют вес от 75 кг до 95 кг и 7 человек имеют вес от 95 до 100 кг. Запишите интервал модального класса.
Итак, все, что вам нужно сделать, это найти группу, которая содержит самую высокую частоту. Было 45 человек с весом от 75 до 95 кг, так что это будет модальная группа.
Таким образом, интервал модального класса составляет от 75 кг до 95 кг.
Пример 2
В таблице частот показано время забега группы спортсменов, принявших участие в забеге на 400 метров. 6 человек завершили забег на 400 метров за время от 45 секунд до 50 секунд, 9 человек завершили забег за время от 50 секунд до 55 секунд, 9 человек завершили забег за время от 55 секунд до 60 секунд, а остальные 3 спортсмена завершил гонку за время от 60 до 65 секунд. Определите интервал модального класса для этих гонок.
Как и в последнем примере, все, что вам нужно сделать, это посмотреть на столбец частоты и выбрать группу, которая содержит самую высокую частоту. Однако в этом примере есть две группы с одинаковой частотой — 9 человек завершили гонку за время от 50 до 55 секунд, а также 9 человек завершили гонку за время от 55 до 60 секунд. Следовательно, существует два модальных класса (известных как бимодальные).
Поэтому интервалы модальных классов составляют от 50 до 55 и от 55 до 60.
Как видите, определение интервала модального класса выполняется очень быстро и легко. Однако вычислить среднее и медиану может быть труднее (см. Ниже, как найти среднее и медиану из таблицы частот).
Вопросы и Ответы
Вопрос: Что такое модальный класс, если числа частот 8, 19, 7, 4, 1?
Ответ: Вы будете искать группу с наибольшей частотой. Итак, это будет группа, соответствующая 19.
Вопрос: Что такое модальный класс, если числа частоты 2,5,7,3,6,2,0,1?
Ответ: Это будет группа, содержащая 7, поскольку 7 — самая высокая частота.
Вопрос: Что такое модальный класс, если числа частоты 0,4,2,7,8,1?
Ответ: Это будет группа, содержащая самую высокую частоту, поэтому, поскольку 8 — это самая высокая частота, то это будет именно эта группа.
Вопрос: Какова модальная оценка для 25,15,30,40,10?
Ответ: Это будет результат с наибольшей частотой. Так как 40 — это самая высокая частота, тогда это будет группа, соответствующая этому числу.
Вопрос: Каков интервал модального класса, если числа частоты 3, 6, 10, 12, 9?
Ответ: Это будет группа с наибольшей частотой.
Таким образом, модальная группа будет иметь 12 в качестве частоты.
Вопрос: Что такое модальный класс, если числа частот 18, 20, 22, 24, 26?
Ответ: Модальная группа — это группа, содержащая наибольшую частоту, которая соответствует группе 26.
Вопрос: Что если модальный класс будет первым или последним?
Ответ: Ни один из них, модальное окно — это группа с наибольшим числом частот.
Вопрос: Как вы решаете режим сгруппированных данных в примере 2?
Ответ: Режим — это группа, в которой частота самая высокая.
В примере 2 есть две группы, которые содержат самую высокую частоту, так что это бимодальные.
Вопрос: Как найти режим для сгруппированных данных с 2 модальными классами?
Ответ: Ответ будет обе эти группы, он будет бимодальным.
Вопрос: Что такое модальный класс, если частоты 14,9,11,2,14?
Ответ: Для модального класса будет две группы (Бимодальные).
Это будут группы, соответствующие 14.
Вопрос: Что такое модальный класс, если числа частоты 3,2,7,8,0?
Ответ: Модальный класс — это группа с самой высокой частотой.
Таким образом, это будет группа, соответствующая 8.
Вопрос: Что такое модальный класс, если частотные числа 7,13,15,6,17,12?
Ответ: Модальный класс — это группа с самой высокой частотой.
Таким образом, это будет группа, соответствующая 17.
Вопрос: Что это за режим, если частоты: 20,12,15,14,11,9,13 и 6?
Ответ: Режимом будет группа с наибольшей частотой.
20 — это самая высокая частота в этом списке, поэтому это будет группа, соответствующая 20.
Вопрос: Что такое модальный класс, если число частот 2, 1, 4, 3?
Ответ: Модальный класс — это группа, содержащая самую высокую частоту.
Поскольку 4 — это наибольшее число, это будет соответствовать группе.
Вопрос: Как нам решать вопрос, который включает два интервала модальных классов?
Ответ: Вы запишите обе группы, поскольку ответ двухрежимный.
Вопрос: Что такое модальный класс, если числа частоты 7,3,3,5,3,7,2? Пожалуйста, объясните, как вычислить среднее значение.
Ответ: Модальный класс — это группа с самой высокой частотой.
В данном случае это две группы, соответствующие 7.
Чтобы вычислить среднее значение, вам нужно будет умножить среднюю точку каждой группы на частоту, сложить этот столбец и разделить ответ на общую частоту.
Вопрос: Каков модальный вес, если числа частоты 3,6,5,1?
Ответ: Это будет вес, соответствующий цифре 6, поскольку 6 — это максимальное число частоты.
Вопрос: Что такое модальный класс, если частотные числа 1, 3, 8, 11, 11, 9, 5 и 2?
Ответ: Будет два режима (двухмодальный).
Две группы, соответствующие 11-м числам.
Вопрос: 6,30,40,16,4,4. Найди режим?
Ответ: Режим — групповое соответствие 40.
Вопрос: Что такое модальный класс, если числа частот 5, 8, 12, 13, 11?
Ответ: Группа, соответствующая 13.
Вопрос: Если наименьшая оценка, полученная в тесте по истории, составляет 18%, а диапазон оценок был 70%. Какая была самая высокая оценка в тесте по истории?
Ответ: Просто добавьте 70% и 18%, чтобы получить 88%.
Вопрос: Каков интервал модального класса, если числа частоты 2,8,9,7,4?
Ответ: Модальная группа — это группа, с которой связана самая высокая частота.
Итак, поскольку 9 — это наибольшее число, тогда это будет группа, соответствующая 9.
Вопрос: Как решить режим в таблице частот?
Ответ: Найдите самую высокую частоту в таблице, и соответствующая ей группа или значение будет режимом.
Вопрос: Что такое модальный класс, если числа частоты 12,10,16,20,18,14,6,4?
Ответ: 20 — это наибольшее число, поэтому группа, соответствующая 20 в таблице частот, будет модальным классом.
Often we may want to calculate the mode of data that is grouped in some way.
Recall that the mode represents the value that occurs most frequently.
For example, suppose we have the following grouped data:
While it’s not possible to calculate the exact mode since we don’t know the raw data values, it is possible to estimate the mode using the following formula:
Mode of Grouped Data = L + W[(Fm – F1)/( (Fm-F1) + (Fm – F2) )]
where:
- L: Lower limit of modal class
- W: Width of modal class
- Fm: Frequency of modal class
- F1: Frequency of class immediately before modal class
- F2: Frequency of class immediately after modal class
Note: The modal class is simply the class with the highest frequency. In the example above, the modal class would be 21-30 since it has the highest frequency.
The following examples show how to calculate the mode of grouped data in different scenarios.
Example 1: Calculate the Mode of Grouped Data
Suppose we have the following frequency distribution that shows the exam scored receive by 40 students in a certain class:
In this example, the modal class is 71-80.
Knowing this, we can calculate the following values:
- L: Lower limit of modal class: 71
- W: Width of modal class: 9
- Fm: Frequency of modal class: 15
- F1: Frequency of class immediately before modal class: 8
- F2: Frequency of class immediately after modal class: 8
We can plug these values into the formula to calculate the mode of the distribution:
- Mode = L + W[(Fm – F1)/( (Fm-F1) + (Fm – F2) )]
- Mode = 71 + 9[(15-8) / ( (15-8) + (15-8) )]
- Mode = 75.5
We estimate that the modal exam score is 75.5.
Example 2: Calculate the Mode of Grouped Data
Suppose we have the following frequency distribution that shows the number of points scored per game by 60 basketball players:
In this example, the modal class is 11-20.
Knowing this, we can calculate the following values:
- L: Lower limit of modal class: 11
- W: Width of modal class: 9
- Fm: Frequency of modal class: 25
- F1: Frequency of class immediately before modal class: 8
- F2: Frequency of class immediately after modal class: 14
We can plug these values into the formula to calculate the mode of the distribution:
- Mode = L + W[(Fm – F1)/( (Fm-F1) + (Fm – F2) )]
- Mode = 11 + 9[(25-8) / ( (25-8) + (25-14) )]
- Mode = 16.46
We estimate that the modal points scored is 16.46.
Additional Resources
The following tutorials explain how to perform other common operations with grouped data:
How to Find Mean & Standard Deviation of Grouped Data
How to Find the Median of Grouped Data
How to Calculate Percentile Rank for Grouped Data
Modal class or the mode class is the class interval in a frequency distribution table that contains the highest frequency. While calculating the mode in statistics, modal class plays a significant role especially while calculating the mode of grouped data. Let us learn more about the modal class, the formula, and solve a few examples.
| 1. | Definition of Modal Class |
| 2. | Modal Class Formula |
| 3. | How to Find the Modal Class? |
| 4. | FAQs on Modal Class |
Definition of Modal Class
In statistics, the class interval with the highest frequency is defined as a modal class. The frequency in the class interval is the highest in a continuous quantitative distribution where the values are grouped into classes with similar dimensions. Mode is not used as a measure of central tendency for continuous quantitative variables since it is more helpful for qualitative variables. Hence, to calculate the mode of grouped data, the middle range of the modal class is used. In other words, mode can’t be obtained just by looking into the frequency, we first need to find out the modal class, in which lies the mode of the given data.
Example: Determine the modal class from the given frequency table
| Balls | 100-90 | 90-80 | 80-70 | 70-60 | 60-50 | 50-40 | 40-30 |
| Boxes | 96 | 32 | 54 | 12 | 27 | 69 | 81 |
Solution:
As we already know that mode is the number that appears the most. To find the modal class, we first arrange the frequencies in ascending order to look for the class with the highest frequency. The class with the highest frequency will be considered as the modal class that also contains the mode. Since the modal class is the class in grouped data that contains the mode. The given frequencies are:
96, 32, 54, 12, 27, 69, 81
Let us arrange them in ascending order to find the highest frequency.
12, 27, 32, 54, 69, 81, 96
The highest frequency from the above list is 96 and the class interval corresponding to it is 100-90.
Therefore, the modal class is 100-90.
Modal Class Formula
To calculate the modal class, the formula for mode of grouped data is used. Let us understand the different terms used in the formula that helps us derive the value of the modal class. For any given data range, let us consider L is the lower limit of the modal class, h is the size of the class interval, fm is the frequency of the modal class, f1 is the frequency of the class preceding the modal class, and f2 is the frequency of the class succeeding the modal class. Here, the modal class is the data interval with the highest frequency. Thus, the mode can be calculated by the formula:
Mode = (L+h frac{left(f_{m}-f_{1}right)}{left(f_{m}-f_{1}right)+left(f_{m}-f_{2}right)})
where,
- L is the lower limit of the modal class
- h is the size of the class interval
- (mathrm{f}_{mathrm{m}}) is the frequency of the modal class
- (mathrm{f}_{mathrm{1}}) is the frequency of the class preceding the modal class
- (mathrm{f}_{mathrm{2}}) is the frequency of the class succeeding the modal class
We might find the above formula written in different forms in some references, as given below,
Mode = (I_{0}) + (left(frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}right) h)
Here,
- I(_0) is the lower limit of the modal class
- h is the size of the class interval
- (mathrm{f}_{mathrm{1}}) is the frequency of the modal class
- (mathrm{f}_{mathrm{0}}) is the frequency of the class preceding the modal class
- (mathrm{f}_{mathrm{2}}) is the frequency of the class succeeding the modal class
How to Find Modal Class?
Let us look at an example of finding the modal class along with the mean using the modal class formula.
| Class Interval | 0−5 | 5−10 | 10−15 | 15−20 | 20−25 |
|---|---|---|---|---|---|
| Frequency | 5 | 3 | 7 | 2 | 6 |
Modal class = 10 — 15 (This is the class with the highest frequency). The Lower limit of the modal class = (L) = 10, Frequency of the modal class = ((f)_{m}) = 7, Frequency of the preceding modal class = ((f)_{1}) = 3, Frequency of the next modal class = ((f)_{2}) = 2, and Size of the class interval = (h) = 5. Thus, the mode can be found by substituting the above values in the formula: Mode = L + h (begin{align}dfrac{(f_m-f_1)}{(f_m-f_1)+(f_m-f_2)}end{align}) .
Thus, Mode = 10 + 5 (begin{align}dfrac{(7-3)}{(7-3)+(7-2)}end{align}) = 10 + 5 × 4/9 = 10 + 20/9 = 10 + 2.22 = 12.22.
Therefore the mode for the above dataset is 12.22.
Related Articles:
- Mean of Grouped Data
- Median of Grouped Data
- Categorical Data
- Range in Statistics
Important Notes on Modal Class
- In a frequency distribution, the class that consists of the highest frequency is known as the modal class.
- The modal class is the class that will consist of the mode.
- The formula to find the modal class is given as (I_{0}) + (left(frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}right) h).
FAQs on Modal Class
What is Modal Class?
Modal class is the class interval that has the highest frequency in the continuous quantitative distribution. The modal class is usually used while finding the mode of grouped data.
What is Modal Class in Mode?
Mode is the number that appears more often and modal class is the class interval with the highest frequency. Hence, the modal class is the class in grouped data that contains the mode.
What If There are 2 Modal Classes?
There can be cases when a number repeats twice on a frequency table that means there are two modes and it is called bimodal. If there are more than 3, it is called multimodal. And these class intervals will be considered as the modal class. If there are numbers that appear the same number of times, then there is no mode.
Can You Have Two Modal Classes?
If there are 2 modes in a frequency table, it is called bimodal. The modal class will be according to the modes since the modal class contains the modes. The two-class intervals will be preceding each other.
How Can You Find the Modal Class?
The modal class is the class interval with the highest frequency in a frequency table. To find the modal class, we need to arrange the frequencies in an ascending order to find the highest frequency. Once the number is found, the class interval corresponding to the number is the modal class.