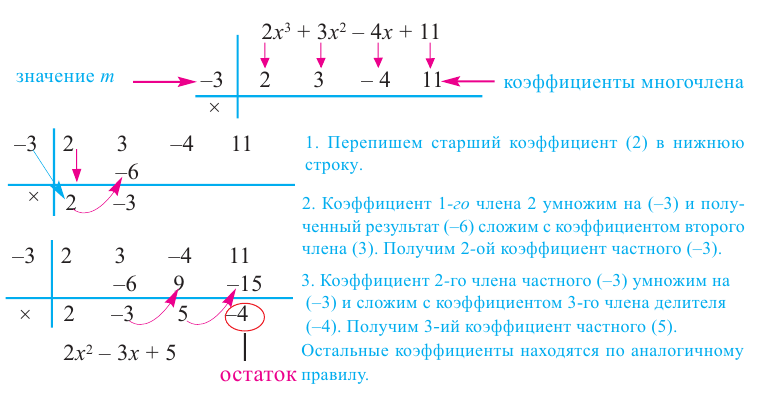
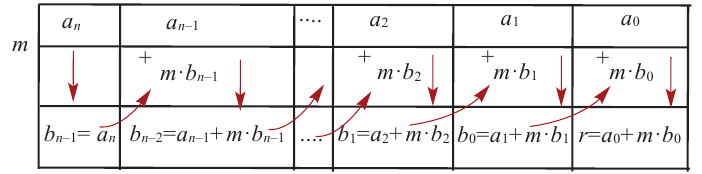
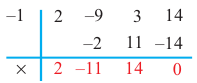
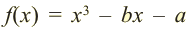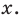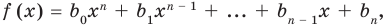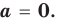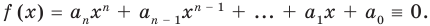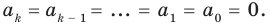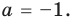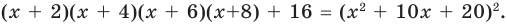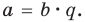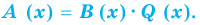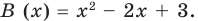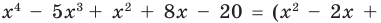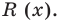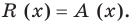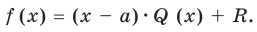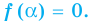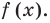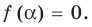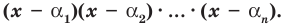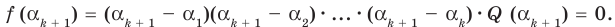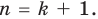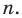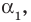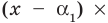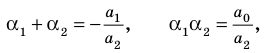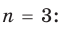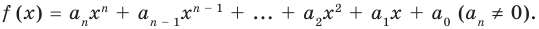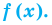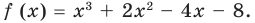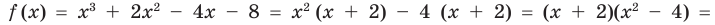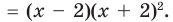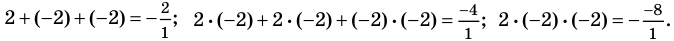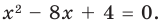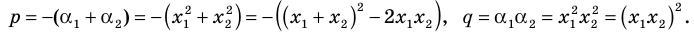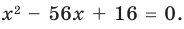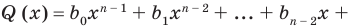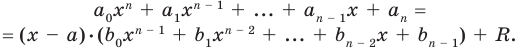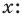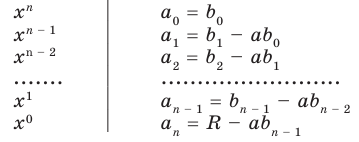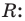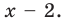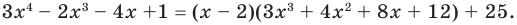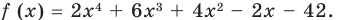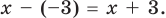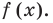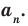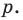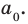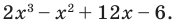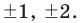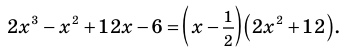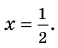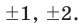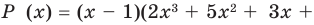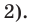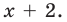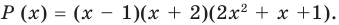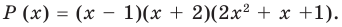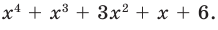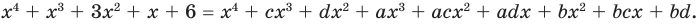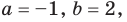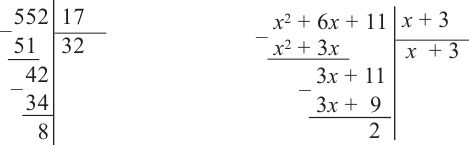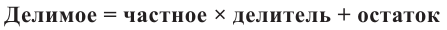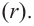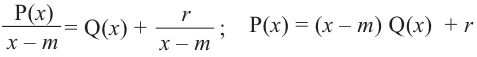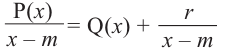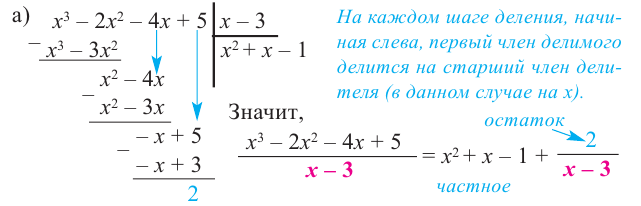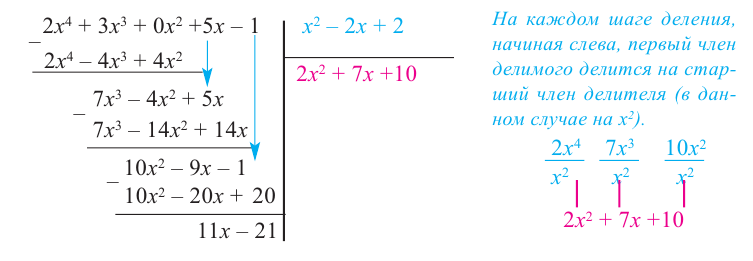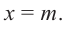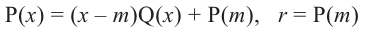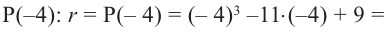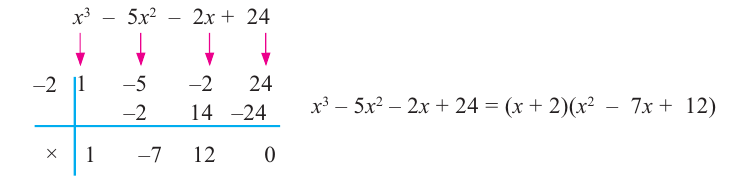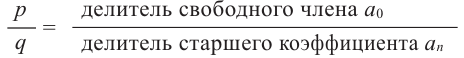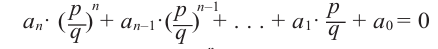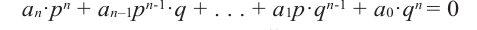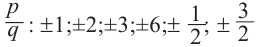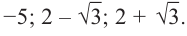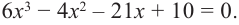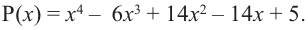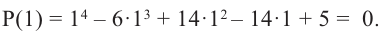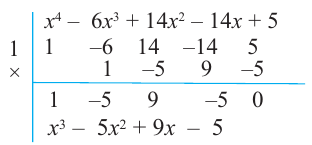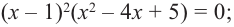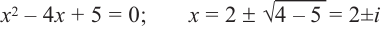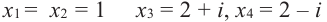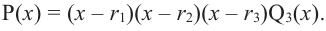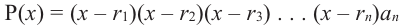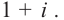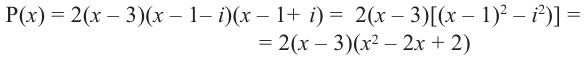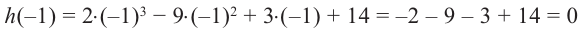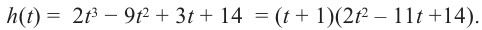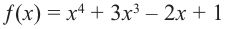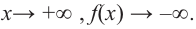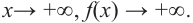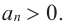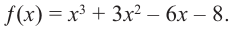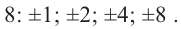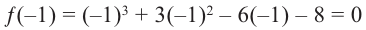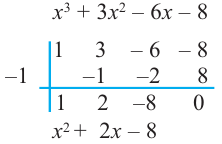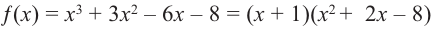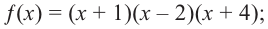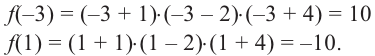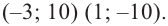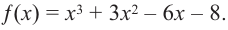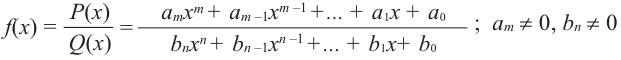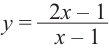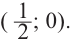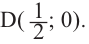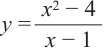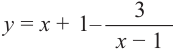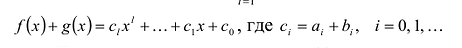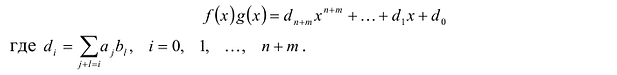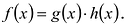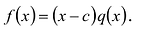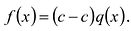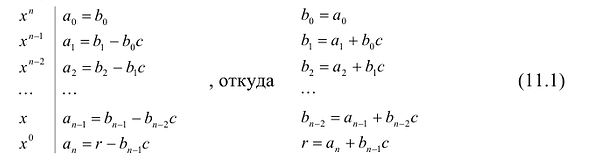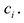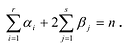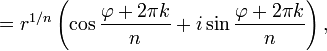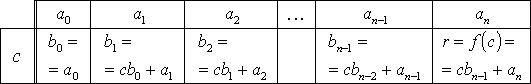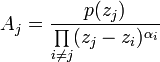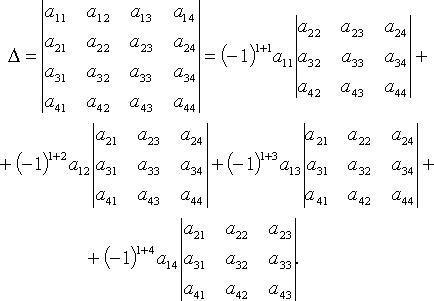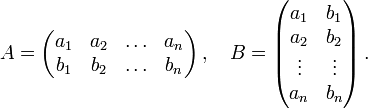Теорема Безу и следствия из неё
19 июля 2022
Теорема Безу позволяет решать уравнения высших степеней, которые на первый взгляд не решаются, и раскладывать на множители многочлены, которые не раскладываются.:)
Формулировка теоремы довольно проста:
Терема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x- color{red}{a}$ равен значению этого многочлена в точке $x= color{red}{a}$:
[r=Pleft( color{red}{a} right)]
На практике нас интересует не сама теорема Безу, а некоторые следствия из неё — именно они помогают решать уравнения и раскладывать многочлены на множители. В этом уроке мы рассмотрим все такие следствия и станем настоящими мастерами в работе с многочленами.
Содержание
- Деление с остатком
- Разложение на множители
- Целые корни многочленов
- Рациональные корни многочленов
- Доказательства
В разных учебниках теорему Безу проходят то в 9-м классе, то в 10-м. Этот урок построен так, что вы поймёте его вне зависимости от школы, класса и учебника.
1. Деление с остатком
Итак, есть многочлен $Pleft( x right)$ и двучлен $x- color{red}{a}$. Разделим $Pleft( x right)$ на $x- color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x- color{red}{a} right)+r]
Теперь найдём значение многочлена $Pleft( x right)$ в точке $x= color{red}{a}$:
[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}- color{red}{a} right)+r=r]
Собственно, мы только что доказали теорему Безу. А заодно подготовили основу для первого важного следствия.
Следствие 1. Деление на произвольный двучлен
Теорема Безу прекрасно работает не только для двучлена $x-color{red}{a}$, но и для любого линейного выражения вида $color{blue}{k}x+color{red}{b}$.
Следствие 1. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $color{blue}{k}x+color{red}{b}$ равен значению этого многочлена в точке $x=-color{red}{b}/ color{blue}{k};$:
[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]
На практике для большей надёжности рекомендуется приравнять двучлен $color{blue}{k}x+color{red}{b}$ к нулю:
[begin{align} color{blue}{k}x+color{red}{b} &=0 \ x &=-frac{color{red}{b}}{color{blue}{k}} \ end{align}]
Затем подставить найденное значение $x=-{color{red}{b}}/{color{blue}{k}};$ в многочлен $Pleft( x right)$ и таким образом найти $Pleft( -{color{red}{b}}/{color{blue}{k}}; right)$:
[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]
Пример 1. Стандартный многочлен
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)=4{{x}^{3}}-3{{x}^{2}}+5x-6]
на двучлен $Tleft( x right)=x-2$.
Решение. Это стандартный двучлен вида $x-color{red}{a}$, поэтому решаем по стандартной теореме Безу, согласно которой остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{2}$ равен $Pleft( color{red}{2} right)$:
[begin{align}r &=Pleft( color{red}{2} right)= \ &=4cdot {color{red}{2}^{3}}-3cdot {color{red}{2}^{2}}+5cdotcolor{red}{2}-6 \ &=32-12+10-6=24 end{align}]
Ответ: 24.
Пример 2. Более сложный многочлен
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)={{left( {{x}^{3}}-2{{x}^{2}}+5 right)}^{3}}{{left( 2x+1 right)}^{5}}]
на двучлен $Tleft( x right)=x+1$.
Решение. Многочлен $Pleft( x right)$ представлен в виде произведения двух других многочленов, которые ещё и возведены в степени. Если раскрыть скобки и привести подобные слагаемые, получится обычный многочлен вида
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
По свойствам степеней найдём степень такого многочлена:
[deg Pleft( x right)=3cdot 3+1cdot 5=14]
Раскрывать скобки и приводить подобные в многочлене 14-й степени долго и трудно, а главное — в этом нет никакой необходимости. Ведь по теореме Безу остаток от деления $Pleft( x right)$ на двучлен $x-color{red}{a}$ всегда равен $Pleft( color{red}{a} right)$ — и не важно, как записан исходный многочлен $Pleft( x right)$.
Для надёжности, чтобы найти $color{red}{a}$, приравняем к нулю двучлен $Tleft( x right)=x+1$:
[begin{align}x+1 &=0 \ x &=color{red}{-1} \ end{align}]
Теперь подставим $x=color{red}{-1}$ в многочлен $Pleft( x right)$ и найдём остаток:
[begin{align}r &=Pleft( color{red}{-1} right)= \ &={{left( {{left( color{red}{-1} right)}^{3}}-2cdot {{left( color{red}{-1} right)}^{2}}+5 right)}^{3}}cdot {{left( 2cdot left( color{red}{-1} right)+1 right)}^{5}}= \ &={{left( -1-2+5 right)}^{3}}cdot {{left( -2+1 right)}^{5}}=-8 end{align}]
Ответ: −8.
Пример 3. Рациональные коэффициенты
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)=3{{x}^{20}}+{{x}^{19}}-7x+1]
на двучлен $Tleft( x right)=3x+1$.
Решение. Воспользуемся Следствием 1 из теоремы Безу. Для надёжности приравняем к нулю двучлен $Tleft( x right)$ и найдём $color{red}{a}$:
[begin{align}3x+1 &=0 \ x &=color{red}{-{1}/{3};} end{align}]
Подставим найденное $x=color{red}{-{1}/{3};}$ в многочлен $Pleft( x right)$ и найдём остаток:
[begin{align} Pleft( color{red}{-frac{1}{3}} right) &=3cdot {{left( color{red}{-frac{1}{3}} right)}^{20}}+{{left( color{red}{-frac{1}{3}} right)}^{19}}-7cdot left( color{red}{-frac{1}{3}} right)+1= \ &=frac{1}{{{3}^{19}}}-frac{1}{{{3}^{19}}}+frac{7}{3}+1=frac{10}{3} end{align}]
Ответ: ${10}/{3};$.
Пример 4. Иррациональные коэффициенты
Не выполняя деления, найдите остаток от деления многочлена
[Pleft( x right)={{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}+64]
на двучлен $Tleft( x right)=left( 1-sqrt{3} right)x+2$.
Решение. Вновь воспользуемся Следствием 1 из теоремы Безу. Приравняем двучлен $Tleft( x right)$ к нулю и найдём $color{red}{a}$:
[left( 1-sqrt{3} right)x+2=0]
Это линейное уравнение с иррациональными коэффициентами. Такое уравнение решается стандартно (см. урок «Линейные уравнения»):
[x=-frac{2}{1-sqrt{3}}=frac{2}{sqrt{3}-1}]
Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряжённое:
[x=frac{2color{blue}{left( sqrt{3}+1 right)}}{left( sqrt{3}-1 right) color{blue}{left( sqrt{3}+1 right)}}=frac{2left( sqrt{3}+1 right)}{2}= color{red}{sqrt{3}+1}]
Степень исходного многочлена: $deg Pleft( x right)=6$. Если подставить в такой многочлен иррациональное число, то это число придётся возводить в шестую степень. Это слишком долго и трудно, поэтому перепишем многочлен $Pleft( x right)$ так:
[begin{align} Pleft( x right) &=left( {{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}-64 right)+128= \ &={{left( {{x}^{2}}-4 right)}^{3}}+128 end{align}]
Мы выделили точный куб разности — классическую формулу сокращённого умножения. Как это работает — см. уроки «Формулы сокращённого умножения» и «Куб суммы и разности».
В такую формулу намного проще подставить $x=color{red}{sqrt{3}+1}$:
[begin{align}Pleft( color{red}{sqrt{3}+1} right) &={{left( {{left( color{red}{sqrt{3}+1} right)}^{2}}-4 right)}^{3}}+128= \ &={{left( {{left( sqrt{3} right)}^{2}}+2sqrt{3}+{{1}^{2}}-4 right)}^{3}}+128= \ &={{left( 2sqrt{3} right)}^{3}}+128= \ &=24sqrt{3}+128 end{align}]
Ответ получился некрасивым, но это и есть искомый остаток от деления.
Ответ: $24sqrt{3}+128$.
2. Разложение на множители
Сейчас будет немного теории, которая может показаться непонятной, но далее на примерах всё встанет на свои места.
Рассмотрим ещё раз деление многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
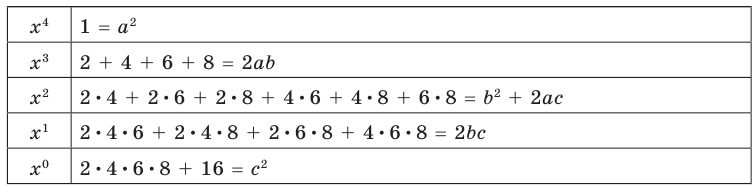
По теореме Безу мы легко найдём остаток $r=Pleft( color{red}{a} right)$. В частности, при $Pleft( color{red}{a} right)=0$ многочлен примет вид
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
А это значит, что многочлен $Pleft( x right)$ разделился на двучлен $x-color{red}{a}$ без остатка, и мы получили разложение на множители.
Кроме того, равенство $Pleft( color{red}{a} right)=0$ означает, что число $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. И это ещё одно замечательное следствие теоремы Безу.
Следствие 2. Корни многочлена и деление
Следствие 2. Число $x=color{red}{a}$ является корнем многочлена $Pleft( x right)$ тогда и только тогда, когда $Pleft( x right)$ делится без остатка на $left( x-color{red}{a} right)$.
На практике это означает, что для разложения многочлена на множители мы просто перебираем разные числа $x=color{red}{a}$ до тех пор, пока не окажется, что $Pleft( color{red}{a} right)=0$. В этот момент многочлен перепишется в виде
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Такой перебор особенно эффективен в сочетании со схемой Горнера (см. урок «Схема Горнера»). Потому что параллельно с вычислением $Pleft( color{red}{a} right)$ мы получаем ещё и коэффициенты нового многочлена $Qleft( x right)$.
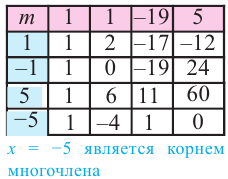
Пример 10. Обычный многочлен
Разложите на множители многочлен
[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}-11x-6]
Решение. Для наглядности отметим синим цветом коэффициенты многочлена $Pleft( x right)$:
[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-11} right)cdot x+left( color{blue}{-6} right)]
Составим из них таблицу для схемы Горнера:
[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline{} & {} & {} & {} & {} & {}\ end{array}]
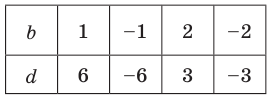
Все коэффициенты целые, поэтому логично проверять целые $x=color{red}{a}$, начиная с самых простых и маленьких чисел:
[x=pm 1; pm 2; pm 3; ldots ]
Проверим $x=color{red}{1}$ и $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline color{red}{1} & 1 & 4 & 1 & -10 & color{red}{-16}\ hline color{red}{-1} & 1 & 2 & -5 & -6 & color{green}{0}\ end{array}]
Проверка числа $x=color{red}{1}$ окончилась неудачей: остаток $r=color{red}{-16}$. Зато проверка $x=color{red}{-1}$ дала остаток $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ является корнем многочлена $Pleft( x right)$, и сам многочлен можно переписать так:
[begin{align}Pleft( x right) &=Qleft( x right)cdot left( x-left( color{red}{-1} right) right) \ &=left( {{x}^{3}}+2{{x}^{2}}-5x-6 right)left( x+1 right) end{align}]
Теперь разложим многочлен $Qleft( x right)$ по схеме Горнера. Проверим ещё раз число $x=color{red}{-1}$:
[begin{array}{r|r|r|r|r|r}{} & 1 & 3 & -3 & -11 & -6\ hline color{red}{-1} & color{blue}{1} & color{blue}{2} & color{blue}{-5} & color{blue}{-6} & color{green}{0}\ hline color{red}{-1} & 1 & 1 & -6 & color{green}{0} & {}\ end{array}]
И вновь получили $r=color{green}{0}$. Исходный многочлен примет вид
[Pleft( x right)=left( {{x}^{2}}+x-6 right){{left( x-1 right)}^{2}}]
В первой скобке стоит квадратный трёхчлен. Разложим его на множители по теореме Виета:
[{{x}^{2}}+x-6=left( x+3 right)left( x-2 right)]
Итого окончательное разложение многочлена $Pleft( x right)$:
[left( x+3 right)left( x-2 right){{left( x-1 right)}^{2}}]
Однако это было довольно простое задание: теорема Безу использовалась лишь в качестве обоснования, почему вместо $Pleft( x right)$ мы пишем $Qleft( x right)left( x-color{red}{a} right)$.
Следующее задание будет намного интереснее.:)
Пример 11. Многочлен с двумя переменными
Разложите на множители многочлен
[Pleft( x,y right)=y{{x}^{2}}+3yx+x-4y-1]
Решение. Это многочлен от двух переменных. Он квадратный относительно переменной $x$ и линейный относительно $y$. Чтобы разложить такой многочлен на множители, сгруппируем его слагаемые относительно переменной $x$:
[Pleft( x,y right)= color{blue}{y}cdot {{x}^{2}}+left( color{blue}{3y+1} right)cdot x+left( color{blue}{-4y-1} right)]
Составляем таблицу:
[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline {} & {} & {} & {}\ end{array}]
Чтобы воспользоваться теоремой Безу, нужно найти такое $x=color{red}{a}$, чтобы $r=Pleft( color{red}{a} right)= color{green}{0}$. Поскольку в роли коэффициентов выступают выражения, содержащие переменную $y$, вновь рассмотрим самые простые варианты, которые приходят в голову:
[x=pm 1; pm y]
Проверим, например, $x=color{red}{1}$:
[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline color{red}{1} & y & 4y+1 & color{green}{0}\ end{array}]
Первая же попытка привела к успеху: $r=color{green}{0}$, поэтому $x=color{red}{1}$ — крень многочлена $Pleft( x,y right)$. Разложим этот многочлен на множители согласно Следствию 2 теоремы Безу:
[Pleft( x,y right)=left( ycdot x+4y+1 right)cdot left( x-color{red}{1} right)]
В первой скобке стоит новый многочлен, линейный по $x$ и по $y$. Его уже нельзя разложить на множители, поэтому ответ окончательный:
[Pleft( x,y right)=left( xy+4y+1 right)left( x-1 right)]
Важное замечание. Строго говоря, линейность многочлена по каждой переменной ещё не означает, что его нельзя разложить на множители. Простой контрпример:
[xy-x+y-1=left( x+1 right)left( y-1 right)]
Однако в нашем случае дальнейшее применение теоремы Безу и проверки по схеме Горнера не даст никаких новых множителей.
3. Целые корни многочленов
До сих пор мы подставляли числа наугад. И если удавалось найти число $x=color{red}{a}$ такое, что $Pleft( color{red}{a} right)=0$, мы объявляли его корнем, а многочлен $Pleft( x right)$ переписывали в виде
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]
Однако с помощью теоремы Безу можно значительно ускорить отыскание корней, отбросив заведомо неподходящие варианты. В этом нам поможет следующее утверждение.
Следствие 3. Целочисленные корни
Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:
[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.
Обратите внимание: старший коэффициент при ${{x}^{n}}$ равен единице. Именно поэтому многочлен $Pleft( x right)$ называется приведённым. Кроме того, все коэффициенты ${{a}_{n-1}},ldots ,{{a}_{0}}$ должны быть целыми числами.
И вот тогда целые корни следует искать среди делителей свободного члена ${{a}_{0}}$.
Пример 5. Простое уравнение
Решите уравнение
[{{x}^{3}}-2{{x}^{2}}-x+2=0]
Решение. Это приведённое кубическое уравнение с целыми коэффициентами. Рассмотрим многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-2} right)cdot {{x}^{2}}+left( color{blue}{-1} right)cdot x+color{blue}{2}]
Если у него есть целые корни, то по Следствию 3 теоремы Безу все они находятся среди делителей свободного члена ${{a}_{0}}=2$. Таких делителей всего четыре:
[x=pm 1; pm 2]
Подставим эти числа в схему Горнера:
[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-2} & color{blue}{-1} & color{blue}{2}\ hline color{red}{1} & 1 & -1 & -2 & color{green}{0}\ hline color{red}{-1} & 1 & -2 & color{green}{0} & {}\ end{array}]
Уже на первом шаге мы получили $r=color{green}{0}$. Следовательно, $x=color{red}{1}$ — корень многочлена $Pleft( x right)$, и сам многочлен можно переписать так:
[Pleft( x right)=left( {{x}^{2}}-x-2 right)left( x-color{red}{1} right)]
Впрочем, если учесть третью строку таблицы, то можно вообще записать
[Pleft( x right)=left( x-2 right)left( x-left( color{red}{-1} right) right)left( x-color{red}{1} right)]
В любом случае, корни многочлена, как и корни уравнения — это числа 2, 1 и −1.
Ответ: $x=1$, $x=-1$, $x=2$.
Формула понижения степени
Итак, с помощью теоремы Безу мы можем:
- Найти целый корень многочлена;
- Разложить исходный многочлен на множители;
- Далее искать корни многочлена степени на единицу меньше.
В самом деле, если $Pleft( color{red}{a} right)=0$, тогда по Следствию 2 теоремы Безу мы переписываем многочлен $Pleft( x right)$ в виде
[Pleft( x right)=Qleft( x right)left( x-color{red}{a} right)]
Далее мы ищем корни многочлена $Qleft( x right)$, степень которого на единицу меньше $Pleft( x right)$.
Этот приём называется понижением степени. Он помогает свести исходный многочлен к квадратному, корни которого легко считаются, например, через дискриминант.
Пример 6. Среднее уравнение
Решите уравнение
[{{x}^{3}}-3{{x}^{2}}-4x+12=0]
Решение. Это уравнение третьей степени. Достаточно найти один корень — далее останется решить квадратное уравнение. Заметим, что многочлен
[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-4} right)cdot x+color{blue}{12}]
является приведённым с целочисленными коэффициентами. По Следствию 3 теоремы Безу все целые корни этого многочлена содержатся среди делителей свободного члена ${{a}_{0}}=12$. Таких делителей довольно много:
[x=pm 1; pm 2; pm 3; pm 4; pm 6; pm 12]
Впрочем, нам достаточно найти всего один корень. Воспользуемся схемой Горнера:
[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-3} & color{blue}{-4} & color{blue}{12}\ hlinecolor{red}{1} & 1 & -2 & -7 & color{red}{5}\ hlinecolor{red}{-1} & 1 & -4 & 0 & color{red}{12}\ hlinecolor{red}{2} & 1 & -1 & -6 & color{green}{0}\ end{array}]
Проверка закончилась неудачей для $x=color{red}{1}$ и $x=color{red}{-1}$. Но для $x=color{red}{2}$ мы нашли то, что искали: остаток $r=color{green}{0}$. Следовательно, $x=color{red}{2}$ — корень многочлена $Pleft( x right)$.
Разложим многочлен на множители согласно теореме Безу:
[Pleft( x right)=left( {{x}^{2}}-x-6 right)left( x-color{red}{2} right)]
В первой скобке стоит квадратный трёхчлен. Его корни легко найти по теореме Виета:
[Pleft( x right)=left( x-3 right)left( x+2 right)left( x-2 right)]
Приравниваем полученное произведение к нулю и решаем уравнение: $x=3$, $x=-2$, $x=2$.
Ответ: $x=2$, $x=-2$, $x=3$.
Пример 7. Сложное уравнение
Решите уравнение
[{{x}^{4}}-{{x}^{3}}-5{{x}^{2}}+3x+2=0]
Решение. Слева приведённый многочлен с целочисленными коэффициентами, поэтому все целые корни находятся среди делителей свободного члена ${{a}_{0}}=2$:
[x=pm 1; pm 2]
Достаточно подобрать два корня — далее уравнение сведётся к квадратному. Воспользуемся схемой Горнера:
[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{-1} & color{blue}{-5} & color{blue}{3} & color{blue}{2}\ hlinecolor{red}{-1} & 1 & -2 & -3 & 6 & color{red}{-4}\ hlinecolor{red}{1} & 1 & 0 & -5 & -2 & color{green}{0}\ hlinecolor{red}{-2} & 1 & -2 & -1 & color{green}{0} & {}\ end{array}]
Получили корни $x=color{red}{1}$ и $x=color{red}{-2}$. Разложим многочлен на множители:
[left( {{x}^{2}}-2x-1 right)left( x-color{red}{1} right)left( x-left( color{red}{-2} right) right)=0]
Решим квадратного уравнение из первой скобки:
[{{x}^{2}}-2x-1=0]
Дискриминант положителен:
[begin{align} D &={{left( -2 right)}^{2}}-4cdot 1cdot left( -1 right)= \ &=4+4=8 end{align}]
Следовательно, уравнение имеет два корня:
[x=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]
Ответ: $x=1$, $x=-2$, $x=1pm sqrt{2}$.
4. Рациональные корни
До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.
Рассмотрим уравнение
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.
Следствие 4. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.
Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
имеют вид $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.
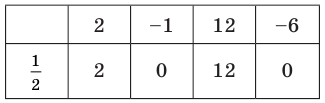
Пример 8. Простой многочлен
Найдите рациональные корни многочлена
[Pleft( x right)=2{{x}^{5}}-{{x}^{4}}+4x-2]
Решение. Делители свободного члена ${{a}_{0}}=-2$:
[p=pm 1; pm 2]
Положительные делители старшего коэффициента ${{a}_{4}}=2$:
[q=1; 2]
Возможные рациональные корни многочлена $Pleft( x right)$ по Следствию 4 теоремы Безу:
[x=pm 1; pm 2; pm {1}/{2};]
Проверять числа $x=color{red}{pm 1}$ нет смысла, поскольку все коэффициенты многочлена $Pleft( x right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.
Остальные числа проверим по схеме Горнера:
[begin{array}{r|r|r|r|r|r|r}{} & color{blue}{2} & color{blue}{-1} & color{blue}{0} & color{blue}{0} & color{blue}{4} & color{blue}{-2}\ hlinecolor{red}{2} & 2 & 3 & 6 & 12 & 28 & color{red}{54}\ hlinecolor{red}{-2} & 2 & -5 & 10 & -20 & 44 & color{red}{-90}\ hline color{red}{{1}/{2};} & 2 & 0 & 0 & 0 & 4 & color{green}{0}\ hline color{red}{-{1}/{2};} & 2 & -2 & 1 & -{1}/{2}; & {17}/{4}; & color{red}{-{33}/{8};}\ end{array}]
Подошло лишь одно число: $x=color{red}{{1}/{2};}$. Следовательно, многочлен имеет лишь один рациональный корень.
Ответ: $x={1}/{2};$.
Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами. При таких обстоятельствах получить $r=color{green}{0}$ уже невозможно.
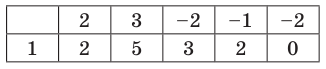
Пример 9. Сложный многочлен
Найдите рациональные корни многочлена
[Pleft( x right)=3{{x}^{7}}+2{{x}^{6}}-5{{x}^{5}}+3{{x}^{3}}-{{x}^{2}}-7x+5]
Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:
[p=pm 1; pm 5]
Положительные делители старшего коэффициента ${{a}_{7}}=3$:
[q=1; 3]
Кандидаты в корни согласно Следствию 4 теоремы Безу:
[x=pm 1; pm 5; pm {1}/{3};; pm {1}/{5};]
Всего восемь кандидатов. Проверим их все по схеме Горнера:
[begin{array}{r|r|r|r|r|c|c|c|c}{} & color{blue}{3} & color{blue}{2} & color{blue}{-5} & color{blue}{0} & color{blue}{3} & color{blue}{-1} & color{blue}{-7} & color{blue}{5}\ hlinecolor{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & color{green}{0}\ hlinecolor{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & color{red}{-6} & {}\ hlinecolor{red}{5} & 3 & 20 & 100 & color{red}{500} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-5} & 3 & -10 & 50 & color{red}{-250} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{1}/{3};} & 3 & 6 & 2 & color{red}{{2}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{1}/{3};} & 3 & 4 & color{red}{-{4}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{5}/{3};} & 3 & 10 & color{red}{{50}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{5}/{3};} & 3 & 0 & 0 & 0 & 3 & -3 & color{green}{0} & {}\ end{array}]
Обратите внимание: для чисел $x=color{red}{5}$ и $x=color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти.
При проверке $x=color{red}{{1}/{3};}$, $x=color{red}{-{1}/{3};}$ и $x=color{red}{{5}/{3};}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.
Итого найдены два рациональных корня: $x=color{red}{1}$ и $x=color{red}{-{5}/{3};}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)
5. Доказательства
Рассмотрим доказательства всех ключевых утверждений сегодняшнего урока.
5.1. Теорема Безу
Мы сформулировали эту теорему в самом начале урока:
Терема Безу. Остаток от деления многочлена
[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
на двучлен $x-color{red}{a}$ равен значению этого многочлена в точке $x=color{red}{a}$:
[r=Pleft( color{red}{a} right)]
Доказательство. Разделим многочлен $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:
[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]
Такое представление всегда однозначно (см. урок «Деление многочленов с остатком»). Здесь многочлен $Qleft( x right)$ — неполное частное, $r$ — остаток, причём
[begin{align}deg r lt deg left( x-color{red}{a} right) &=1 \ deg r &=0 \ end{align}]
Другими словами, остаток $r$ — это просто число.
Теперь найдём значение $Pleft( x right)$ в точке $x=color{red}{a}$:
[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}-color{red}{a} right)+r=r]
Теорема Безу доказана. Однако её доказательство опирается на единственность деления с остатком.
5.2. Целочисленные корни
Целочисленные корни приведённого многочлена с целыми коэффициентами следует искать среди делителей свободного члена.
Следствие 3. Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:
[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]
Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.
Доказательство. Пусть $color{red}{b}in mathbb{Z}$ — корень многочлена $Pleft( x right)$, т.е. $Pleft( color{red}{b} right)=0$. Подставим число $x=color{red}{b}$ в формулу многочлена и получим уравнение:
[{color{red}{b}^{n}}+{{a}_{n-1}}{color{red}{b}^{n-1}}+ldots +{{a}_{1}}color{red}{b}+{{a}_{0}}=0]
Перенесём последнее слагаемое вправо, а слева из оставшихся слагаемых вынесем множитель $color{red}{b}$ за скобку:
[color{red}{b}cdot left( {color{red}{b}^{n-1}}+{{a}_{n-1}}{color{red}{b}^{n-2}}+ldots +{{a}_{1}} right)=-{{a}_{0}}]
Поскольку $-{{a}_{0}}in mathbb{Z}$, а слева стоят два целочисленных множителя, получаем, что число $-{{a}_{0}}$ делится на $color{red}{b}$. Следовательно, свободный член ${{a}_{0}}$ тоже делится на $color{red}{b}$, что и требовалось доказать.
5.3. Рациональные корни
Рассмотрим уравнение
[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]
где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.
Утверждение. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения $Pleft( x right)=0$, то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.
Доказательство. Подставим число $x=color{red}{p}/color{blue}{q};$ в исходное уравнение. Поскольку $x=color{red}{p}/color{blue}{q};$ — корень, уравнение обратится в верное числовое равенство:
[{{a}_{n}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n}}+{{a}_{n-1}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n-1}}+ldots +{{a}_{1}}cdot frac{color{red}{p}}{color{blue}{q}}+{{a}_{0}}=0]
Домножим обе части на ${color{blue}{q}^{n}}$. Получим
[{{a}_{n}}{color{red}{p}^{n}}+{{a}_{n-1}}{color{red}{p}^{n-1}}color{blue}{q}+ldots +{{a}_{1}}color{red}{p}{color{blue}{q}^{n-1}}+{{a}_{0}}{color{blue}{q}^{n}}=0]
Перенесём последнее слагаемое ${{a}_{0}}{color{blue}{q}^{n}}$ вправо, а в левой части из оставшихся слагаемых вынесем множитель $color{red}{p}$ за скобку:
[color{red}{p}left( {{a}_{n}}{color{red}{p}^{n-1}}+{{a}_{n-1}}{color{red}{p}^{n-2}}color{blue}{q}+ldots +{{a}_{1}}{color{blue}{q}^{n-1}} right)=-{{a}_{0}}{color{blue}{q}^{n}}]
Слева и справа от знака равенства стоят целые числа, поскольку все слагаемые и множители являются целыми. Мы видим, что левая часть делится на $color{red}{p}$. Следовательно, правая часть тоже делится на $color{red}{p}$:
[-{{a}_{0}}{color{blue}{q}^{n}} vdots color{red}{p}]
По условию теоремы дробь $color{red}{p}/color{blue}{q};$ несократима. Следовательно, числа $color{blue}{q}$ и $color{red}{p}$ не имеют общих делителей, и единственный возможный вариант — это когда ${{a}_{0}}$ делится на $color{red}{p}$.
Аналогично доказывается, что старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$. Теорема доказана.
Вот и всё.:)
Смотрите также:
- Схема Горнера
- Деление многочленов уголком
- Теорема Виета
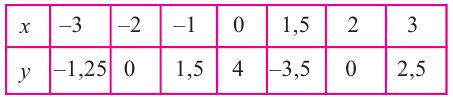
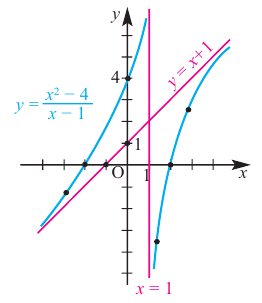
- Задача B3 — работа с графиками
- Метод коэффициентов, часть 2
- Нестандартная задача B2: студенты, гонорары и налоги
В данной публикации мы рассмотрим теорему Безу, с помощью которой можно найти остаток от деления многочлена на двучлен, а также, научимся применять ее на практике для решения примеров.
- Формулировка теоремы Безу
- Решение примеров
Формулировка теоремы Безу
Остаток от деления многочлена P(x) на двучлен (x-a) равняется P(a).
Pn(x) = a0xn + a1xn-1 + … + an-1x + an
Следствие из теоремы:
Число a является корнем многочлена P(x) исключительно в том случае, если многочлен P(x) без остатка делится на двучлен (x-a).
Из этого следствия вытекает следующее утверждение: множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения P(x)=0.
Решение примеров
Пример 1
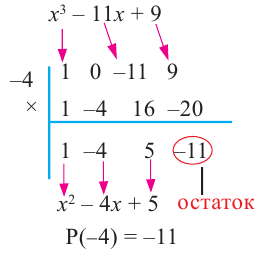
Найдите остаток от деления многочлена 5x2 – 3x + 7 на двучлен (x – 2).
Решение
Чтобы найти остаток от деления, согласно теореме Безу, требуется найти значение многочлена в точке a (т.е. вместо x подставляем значение a, которое в нашем случае равняется числу 2).
5 ⋅ 22 – 3 ⋅ 2 + 7 = 21.
Т.е. остаток равен 21.
Пример 2
Используя теорему Безу выясните, делится ли многочлен 3x4 + 15x – 11 на двучлен (x + 3) без остатка.
Решение
В данном случае a = -3. Подставляем это число вместо x в многочлен и получаем:
3 ⋅ (-3)4 + 15 ⋅ (-3) – 11 = 187.
Это значит, что деление без остатка невозможно.
Пример 3
Выясните, при каком значении y, многочлен x23 + yx + 16 без остатка делится на двучлен (x + 1).
Решение
Применив теорему Безу, находим нулевой остаток от деления:
(-1)23 + y ⋅ (-1) + 16 = 0
-1 – y + 16 = 0
y = 15
Таким образом, при y, равном 15, остаток будет равен 0.
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен — это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной
По определению одночлена числа и буквы (в нашем случае одна буква — 
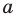
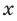
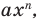
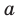
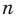
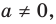
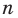
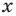
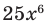
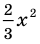
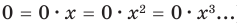
По определению многочлен от одной переменной 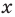
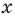
многочленом от одной переменной 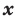
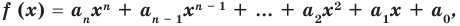
где коэффициенты 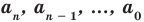
Если 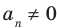
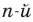
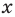
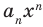
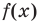
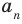
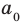
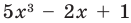
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 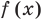
где 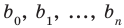
Теорема 1. Одночлены 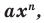
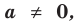
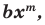
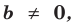
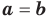
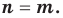
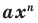
Поскольку равенство одночленов
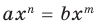
выполняется при всех значениях 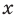
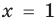
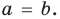
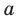
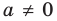
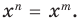
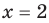
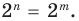
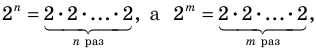
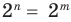
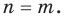
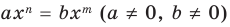
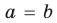
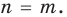
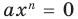
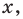
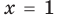
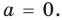
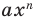
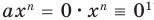
Далее любой одночлен вида 
Теорема 2. Если многочлен 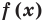
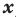
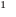
Для доказательства используем метод математической индукции. Пусть
При 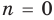
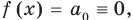
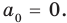
Предположим, что при 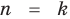
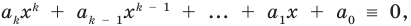
Докажем, что данное утверждение выполняется и при 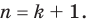
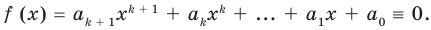
Поскольку равенство (3) выполняется при всех значениях 
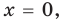
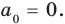
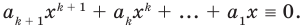

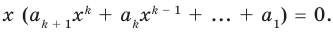
Равенство (4) должно выполняться при всех значениях 
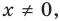
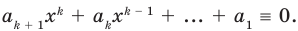
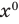
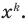
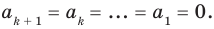
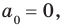
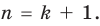
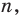
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 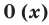
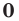
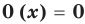
Теорема 3. Если два многочлена 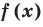
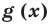
Пусть многочлен 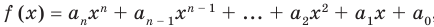
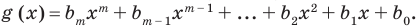
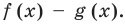
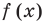
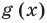
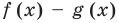
Но 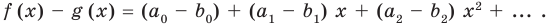
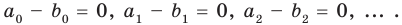
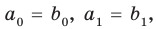
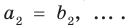
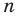
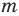
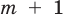
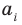
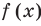
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 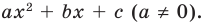
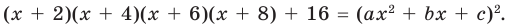
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 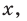
Из первого равенства получаем 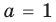
При 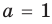
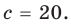
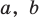
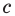
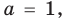
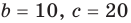
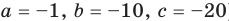
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 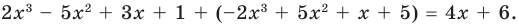
Например, 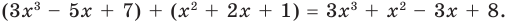
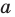
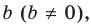
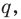
Определение: Многочлен 
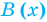
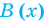

Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен 








Например, поскольку 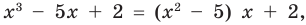
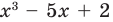
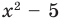
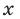
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 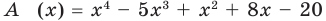
Решение:
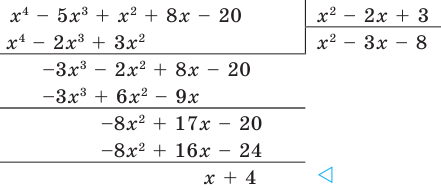
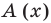
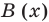
Если обозначить результат выполнения первого шага алгоритма через 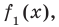
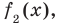
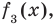
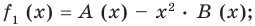
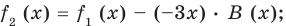
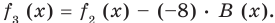
Сложим почленно равенства (1), (2), (3) и получим
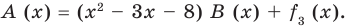
Учитывая, что степень многочлена 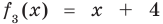
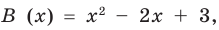
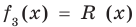
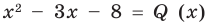
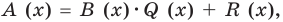
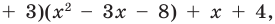
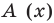
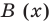
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 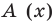
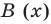
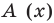
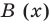
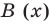
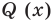
Отметим, что в случае, когда степень делимого 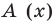
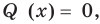
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 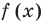
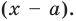
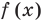
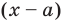
Это равенство выполняется тождественно, то есть при любом значении 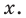
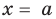
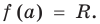
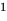
Теорема 1 (теорема Безу). Остаток от деления многочлена 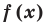
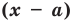
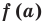
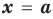
Пример №2
Докажите, что 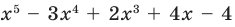
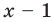
Решение:
► Подставив в 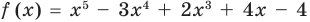
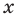
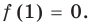
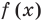

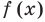

Определение: Число 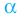
Если многочлен 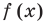

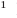
Действительно, если 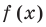
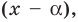

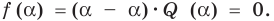
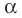
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 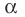
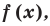
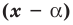
По теореме Безу остаток от деления 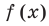

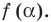
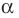
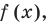
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 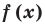
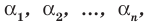
Для доказательства используем метод математической индукции.
При 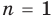
Допустим, что утверждение справедливо при 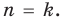
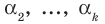
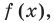
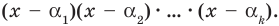
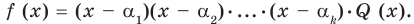
Докажем, что утверждение теоремы справедливо и при 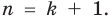
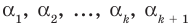
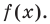
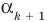
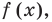
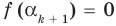
По условию все корни 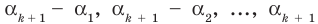
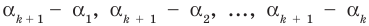
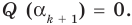
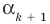
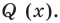
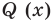
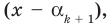
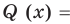
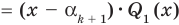
Это означает, что 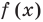
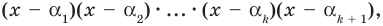
Таким образом, теорема справедлива для любого натурального
Следствие. Многочлен степени 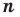
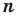
Допустим, что многочлен 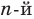
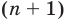
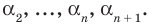
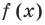
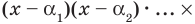
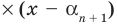
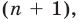
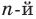
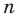
Пусть теперь многочлен 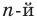
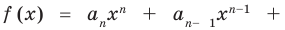
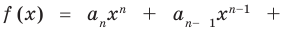
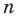
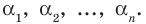
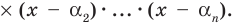
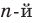
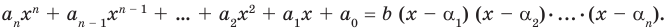
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 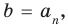
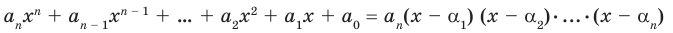
Сравнивая коэффициенты при одинаковых степенях 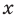
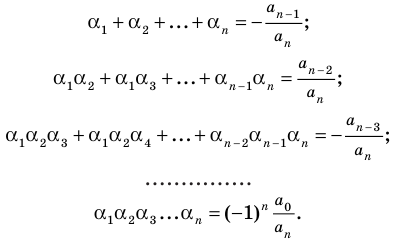
Например, при 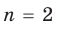
а при
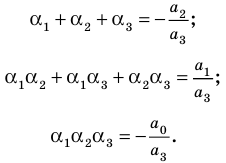
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 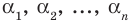
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 
Если многочлен 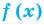
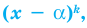
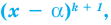


Например, если произведение 
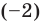
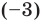
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена
Решение:
►
Поэтому 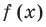
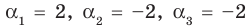
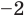
Проверим справедливость формулы (5). В нашем случае: 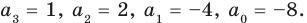
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения
Решение:
► Обозначим корни уравнения 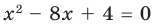
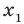
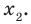
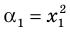
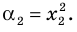
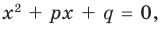
По формулам Виета имеем 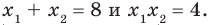
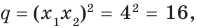
Схема Горнера
Делить многочлен 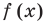
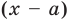
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 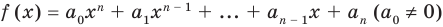
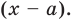
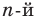
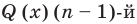
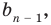
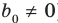
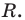
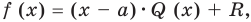
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях
Найдем из этих равенств коэффициенты 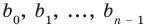
Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 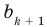
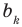
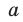
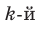
Пример №5
Разделите по схеме Горнера многочлен 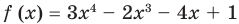
Решение:
► Запишем сначала все коэффициенты многочлена 
Таким образом,
Пример №6
Проверьте, является ли 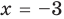
Решение:
► По теореме Безу остаток от деления многочлена 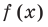
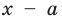
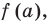
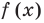
Поскольку 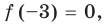
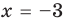
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 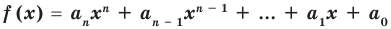
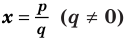
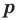
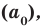
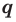
Если 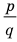
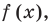
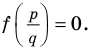
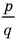
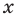
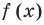
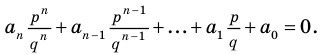
Умножим обе части равенства (1) на 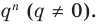
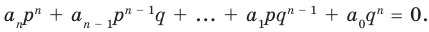
В равенстве (2) все слагаемые, кроме последнего, делятся на 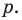
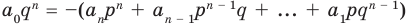
Но когда мы записываем рациональное число в виде 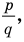
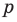
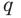
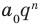
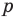
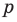
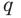
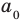
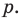
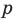
Аналогично все слагаемые равенства (2), кроме первого, делятся на 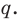
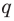
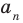
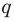
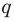
Отметим два следствия из этой теоремы. Если взять 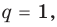
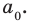
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 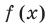
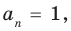
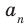
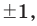
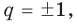
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена
Решение:
► Пусть несократимая дробь 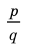
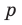
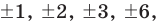
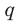
Таким образом, рациональные корни многочлена необходимо искать среди чисел 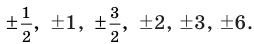
При 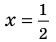
Кроме того, по схеме Горнера можно записать, что
Многочлен 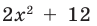
Пример №8
Разложите многочлен 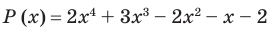
Решение:
► Ищем целые корни многочлена среди делителей свободного члена:
Подходит 1. Делим 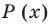

Тогда
Ищем целые корни кубического многочлена 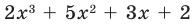
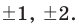
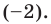
Имеем
Квадратный трехчлен 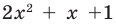
Ответ:
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 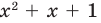
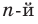
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
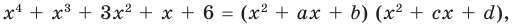
где 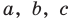
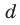
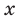
Получаем систему
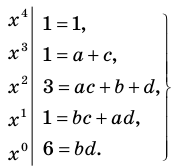
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 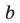
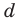
Коэффициенты 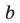
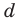
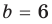
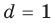
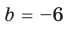
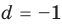
Для каждой пары значений 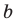
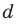
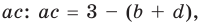
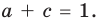
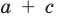
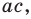
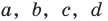
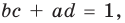
Как видим, системе (4) удовлетворяет набор целых чисел 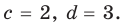
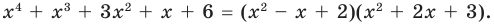
Поскольку квадратные трехчлены 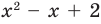
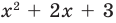
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 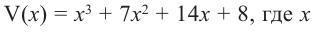
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 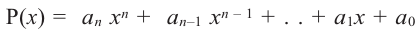
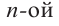
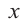
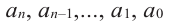
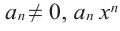
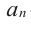
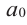
Деление целого числа па целое число можно проверить равенством
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 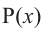
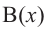
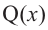
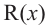
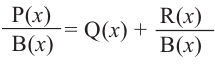
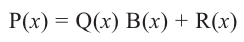
Здесь, степень многочлена 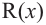
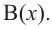
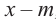
В этом случае:
Пример №10
а) Разделите многочлен 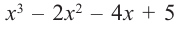
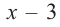
Ответ запишите в виде
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
b) При этом 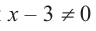
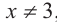
c) Должно выполняться тождество
Пример №11
Разделите 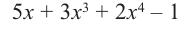
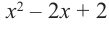
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0.
Пример №12
1) Исследуйте деление столбиком многочлена 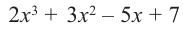
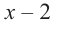
2) На каждом шаге деления делимое делится на старший член делителя, на 
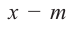
При делении многочлена на двучлен вида 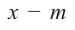
Пример №13
Разделите многочлен 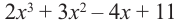
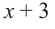
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 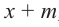
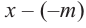
Запишем двучлен 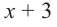
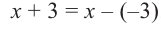
Таким образом, для делимого 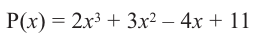
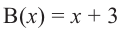
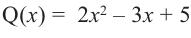
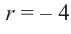
Деление можно записать в виде: 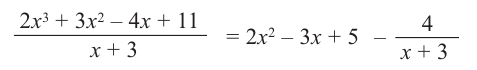
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 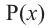
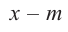
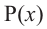
Доказательство: В равенстве 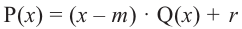
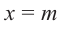
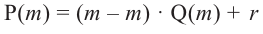
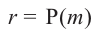
Пример №14
Найдите остаток от деления многочлена 
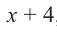
Решение: запишем делитель в виде 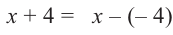
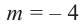
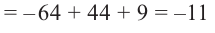
Проверим решение.
Теорема о разложении многочлена на множители
Значения переменной 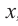
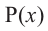
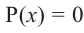
Теорема. Если число 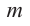
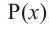
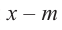
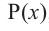
Действительно, если 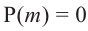
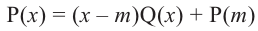
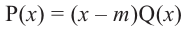
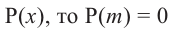
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 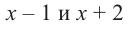
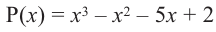
Решение: вычислим значение многочлена 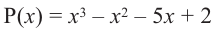
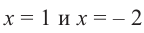
Значит, 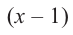
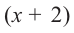
Пример №16
Зная, что 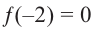
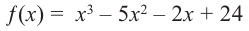
Решение: так как 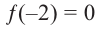
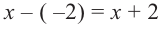
Учитывая, что 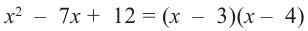
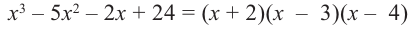
Отсюда получаем, что 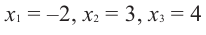
Примечание: Если многочлен задан в виде 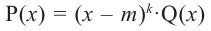
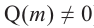
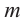
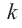
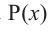
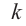
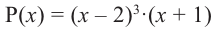
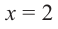
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 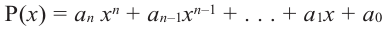
Доказательство. Пусть несократимая дробь 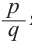
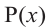
Умножим обе части равенства на
Так как в последнем равенстве каждый член, кроме члена 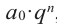
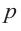
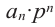
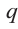
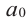
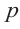
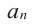
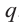
Пример №17
Найдите рациональные корни многочлена 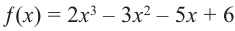
Решение: свободный член 6, старший коэффициент 2.
Для 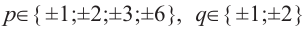
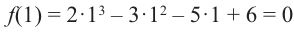
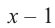
Так как, 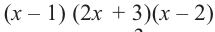
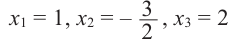
Следствие 1. Если старший коэффициент 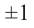
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 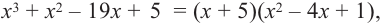
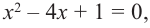
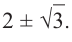
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 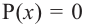
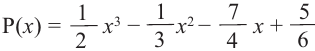
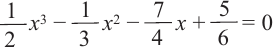
уравнение
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 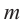
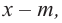
3. Для данного многочлена при помощи синтетического деления на двучлен 
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 
Проверим: 
Основная теорема алгебры
Покажем на примере, что многочлен 
Пример №19
Найдите все корни многочлена
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
Значит, 
В выражении 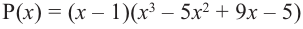
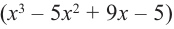
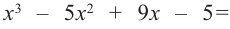
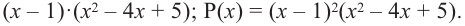
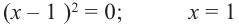
Корни:
Во всех рассмотренных нами примерах уравнение 
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 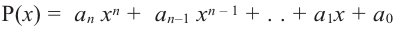
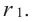
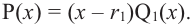
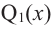
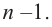
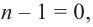
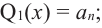
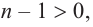
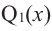
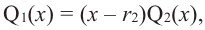
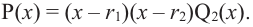
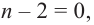
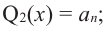
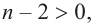
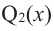
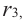
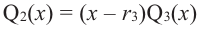
Продолжая процесс 
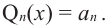
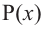
здесь числа 
Следствие. Многочлен 
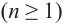
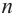
Отметим, что если комплексное число 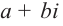
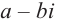
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 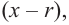
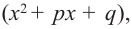
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и
Решение: так как число 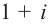
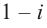
- Заказать решение задач по высшей математике
Пример №21
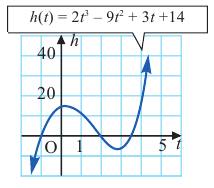
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 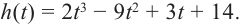
Решение: во всех случаях, кроме значений 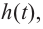
1. Проверим, является ли число 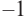
2. Число 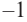
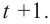
Учитывая, что 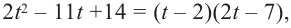
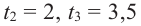
Функция-многочлен
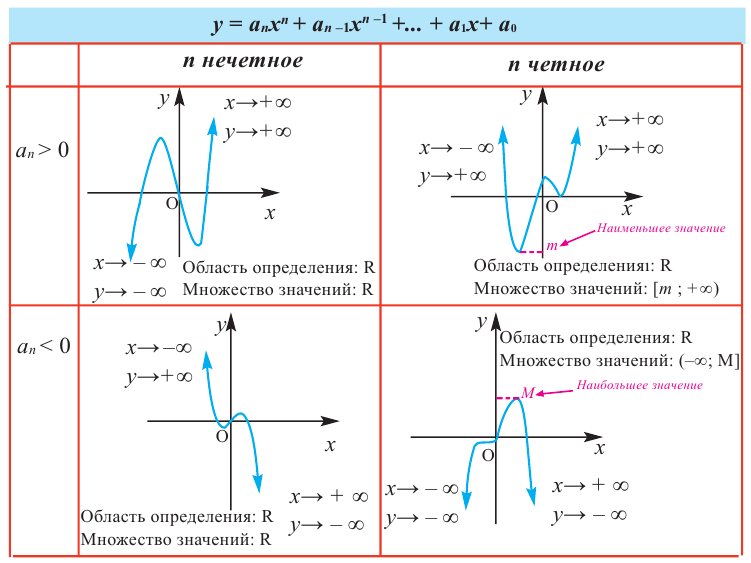
График функции-многочлен
В стандартном виде функция — многочлен записывается как 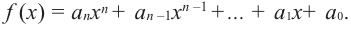
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 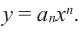
Пример №22
Определите характер поведения функции — многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 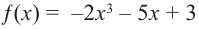
Решение: а) степень многочлена 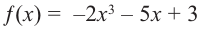
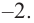
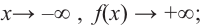
b) степень многочлена 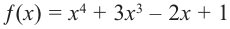
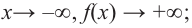
Пример №23
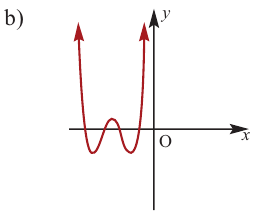
По графику определите как ведет себя функция — многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
Решение:
при
при
Многочлен нечетной степени
Решение:
при
при
Многочлен четной степени
Отметим, что если 
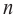
Алгоритм построения эскиза графика функции — многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
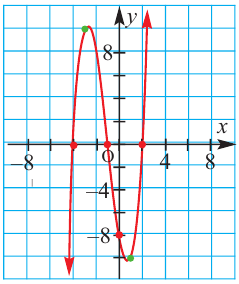
Пример №24
Постройте график функции
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа
Проверим 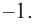
Значит, двучлен 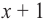
Зная, что 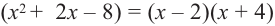
Отсюда находим нули 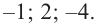
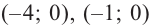
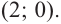
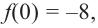
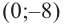
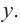
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 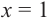
Отметим точки
3. Определим, как меняется график при уменьшении или увеличении значений 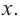
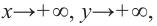
4. Соединим отмеченные точки и получим схематический график функции
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
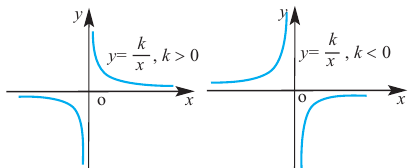
Самым простым примером рациональной функции является функция
График функции 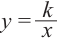
При стремлении значений 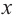
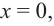
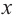
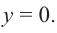
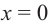
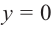
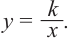
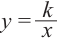
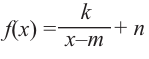
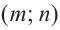
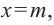
Пример №25
Постройте график функции
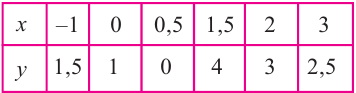
Решение: точки пересечения с осью 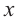
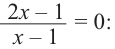
При 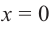
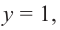
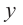
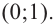
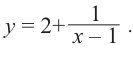
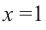
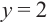
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 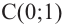
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 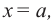
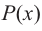
Для 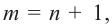
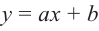
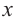
Пример №26
Найдите асимптоты и схематично изобразите график функции
Решение: Точки пересечения с осью 
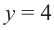
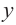
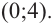
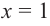
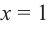
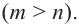
Для больших, но модулю, значений 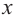
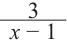
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
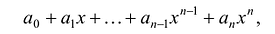
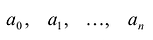
Если коэффициент 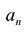
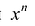
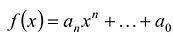
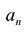
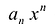
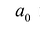
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 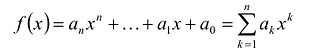
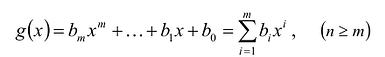
Произведением многочленов 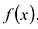
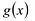
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 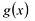
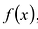
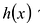
Теорема о делении с остатком
Для любых многочленов 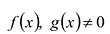
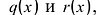
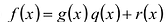
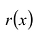
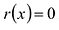
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит 
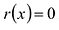
Число с называется корнем многочлена 

Теорема Безу
Число с является корнем многочлена 

Пусть с — корень многочлена 


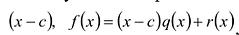
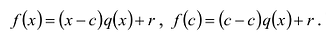

Обратно, пусть (х-с) делит 
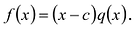
Следствие. Остаток от деления многочлена 
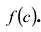
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена 
Многочлен 
Пусть 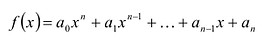
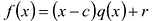
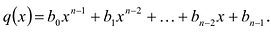
Число с-называется корнем кратности к многочлена 
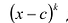

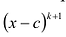

Чтобы поверить, будет ли число с корнем многочлена 

Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 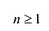
где 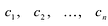

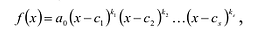
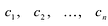

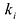
Если многочлен 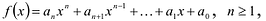
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 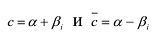


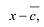
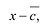

Утверждение 2. Многочлен с действительными коэффициентами степени 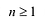
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где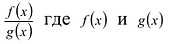
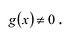

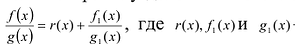
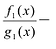
Лемма 1, Если 
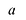
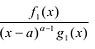
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если 
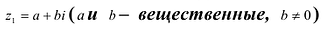
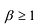
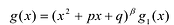
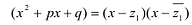
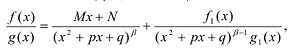
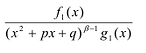
Рациональные дроби вида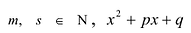
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 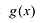
Число неизвестных 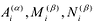
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Линейный оператор — свойства и определение
Многочленом с одной переменной называется выражение вида
`P(x) = a_n x^n + a_(n-1) x^(n-1) +a_(n-2) x^(n-2) + … + a_2 x^2 + a_1 x + a_0 (a_n != 0)`. (8)
Числа `a_0`, `a_1`, `…`, `a_n` — это коэффициенты многочлена; `a_n` называют старшим коэффициентом, `a_0` — свободным членом.
Степенью многочлена называют наибольшую степень переменной, входящую в многочлен.
Например, степень многочлена `P = x^4 — x^3 — x^2 + 2x + 1` равна `4`; степень многочлена `25 + x^5 — 3x` равна `5`; степень многочлена `17` равна `0`, т. к. переменная в это выражение не входит; наконец, выражение `3x^2 + x +5+ 2/x` многочленом не является, поэтому о его степени говорить бессмысленно. Многочлен `P(x) = 0` называют нулевым многочленом. Степень нулевого многочлена не определена.
Два многочлена называются равными, если равны все их коэффициенты. Многочлен равен нулю, если все его коэффициенты равны нулю.
Число `a` называется корнем многочлена `F(x)`, если `F(alpha) = 0`.
Приведём основные сведения о многочленах.
Для любых двух многочленов `F(x)` и `G(x)` существует единственная пара многочленов `P(x)` (частное) и `Q(x)` (остаток) такая, что `F(x) = G(x) * P(x) + Q(x)`, причём степень остатка `Q(x)` меньше степени делителя `G(x)`, или `Q(x)` есть нулевой многочлен. Покажем, как на практике находят частное и остаток от деления многочленов.
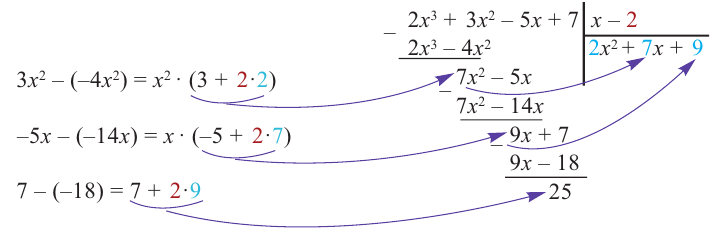
Разделите с остатком многочлен `F(x) = 18x^5 + 27x^4 -37x^3 — 14x + 20`
на многочлен `G(x) = 2x^2 + 3x -5`.
Процедура деления многочленов очень похожа на деление целых чисел. Если степень делимого не меньше степени делителя, то делаем следующее: делим старший член многочлена `F(x)` на старший член многочлена `G(x)`, получившийся результат записываем в частное. Умножаем результат на весь делитель `G(x)` и вычитаем полученное из исходного многочлена `F(x)`. После этих действий член со старшей степенью `x` сокращается. Если в результате вычитания у оставшегося многочлена степень не меньше, чем степень делителя, то можно сделать ещё один шаг деления и т. д.
Деление закончится тогда, когда степень делимого будет меньше степени делителя. В случае, когда в делимом отсутствуют некоторые степени переменных, для удобства записи лучше оставить пустые места для соответствующих членов (хотя это не обязательно).
Вернёмся к нашему примеру. Первый член частного равен `(18x^5)/(2x^2) = 9x^3`. При умножении на делитель `2x^2 +3x-5` получаем `18x^5 + 27x^4 — 45x^3`. После вычитания из исходного многочлена от него остаётся `8x^3 -14x +20`. Степень многочлена, оставшегося после вычитания, равна `3`. Это больше степени делителя, поэтому можно сделать следующий шаг деления. Делим `8x^3` на `2x^2` и получаем `4x`, умножаем `4x` на `2x^2 +3x-5`, получаем `8x^3 +12x^2 -20`; вычитаем этот многочлен из `8x^3 -14x +20` и т. д.
Частное равно `9x^3 +4x -6`; остаток равен `24x-10`.
Таким образом, `18x^5 + 27x^4 — 37x^3 -14x + 20 = (2x^2 + 3x — 5)(9x^3 + 4x — 6) + (24x — 10)`.
1) Теорема Безу. Остаток от деления многочлена `F(x)` на многочлен `(x-alpha)` равен `F(alpha)`.
2) Число `alpha` является корнем многочлена `F(x)` тогда и только тогда, когда многочлен `F(x)` делится на многочлен `(x-alpha)`.
3) Если `alpha` и `beta` — различные корни многочлена `F(x)`, то он делится на многочлен `(x- alpha)(x- beta)`.
4) Многочлен степени `n` не может иметь более `n` корней.
1) Разделим с остатком многочлен `F(x)` на многочлен `(x-alpha)`. Тогда остаток либо равен нулю, либо является многочленом нулевой степени (т. к. степень остатка меньше степени делителя, а степень делителя равна `1`). Поэтому можно записать, что
`F(x) = (x-alpha) G(x) +C` (9)
Через `G(x)` здесь обозначено частное от деления, вид которого нас не интересует.
Равенство (9) верно при всех значениях `x`. Подставим в него `x=alpha`.
Тогда `F(alpha) = (alpha — alpha)G(alpha) + C`, или `F(alpha) = C`.
Подставим `C=F(alpha)` в (9) и получим
`F(x) = (x — alpha) G (x) + F(alpha)`. (10)
Первая часть доказана.
2) Из (10) следует, что `F(x)` делится на `(x — alpha)` тогда и только тогда, когда `F(alpha) = 0`, т. е. тогда и только тогда, когда `alpha` есть корень многочлена `F(x)`.
3) `alpha` — корень `F(x) => F(x)` делится на `(x- alpha) => F(x) = (x- alpha) G(x)`. Подставим в последнее равенство (которое верно для всех значений переменной `x`) `x= beta`. Тогда `F(beta) = (beta — alpha) G(beta)`.
`F(beta) = 0` (т. к. `beta` -корень `F(x)`), поэтому `(beta — alpha)G(beta) = 0 =>G(beta) = 0` (т. к. `beta != alpha`); отсюда `G(x)` делится на `(x- beta)`, т. е. `G(x) = H(x) * (x- beta)`. Подведём итог: `F(x) = (x- alpha) G(x) = (x -alpha)(x- beta) H(x)`, т. е. `F(x)` делится на `(x- alpha)(x- beta)`.
4) Теперь становится понятным, что многочлен степени `n` не может иметь больше, чем `n` корней.
Остатки от деления многочлена `F(x)` на многочлены `(x-3)` и `(x+5)` равны `2` и `(-9)` соответственно. Найдите остаток от деления многочлена `F(x)` на многочлен `x^2 + 2x -15`.
Заметим, что `x^2 + 2x -15 = (x-3)(x+5)`.
По теореме Безу `F(3) = 2`; `F(-5) =-9`.
Поделим `F(x)` с остатком на `x^2 + 2x -15`:
`F(x) = (x^2 + 2x — 15)G(x) + r(x)`.
Степень остатка не превосходит степени делителя, поэтому остаток – это либо многочлен первой степени, либо нулевой степени, либо равен нулю. В любом случае, остаток представим в виде `r(x) = ax +b` (если `a!= 0`, то получим многочлен первой степени; если `a=0`, `b!=0`, то будет многочлен нулевой степени; если `a=b=0`, то получим нулевой многочлен). Итак,
`F(x) = (x^2 + 2x-15)G(x) + ax+b`. (11)
Подставим в равенство (11) `x=3` и `x=-5`:
`F(3) = 0 * G(3) + 3a + b`; `F(-5)=0 * G(-5) -5a+b`, откуда $$ left{begin{array}{l}3a+b=2,\ -5a+b=-9.end{array}right.$$
Решая эту систему, нахоим, что `a=(11)/8`, `b=- (17)/8`.
Остаток равен `(11)/8 x — (17)/8`.
Докажите, что
$$ sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}=4$$. (12)
Пусть $$ sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}=x$$. Возведём обе части этого равенства в куб и преобразуем:
$$ 26-15sqrt{3}+3sqrt[3]{{left(26-15sqrt{3}right)}^{2}}sqrt[3]{26+15sqrt{3}}+3sqrt[3]{26-15sqrt{3}}sqrt[3]{{left(26+15sqrt{3}right)}^{2}}+26+15sqrt{3}={x}^{3}$$;
$$ 52+3sqrt[3]{26-15sqrt{3}}sqrt[3]{26+15sqrt{3}}left(sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}right)={x}^{3}$$;
$$ 52+3sqrt[3]{{26}^{2}-{left(15sqrt{3}right)}^{2}}left(sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}right)={x}^{3}$$;
$$ 52+3left(sqrt[3]{26-15sqrt{3}}+sqrt[3]{26+15sqrt{3}}right)={x}^{3}$$;
`52+3x=x^3`;
`x^3-3x-52=0`. (13)
Число `x=4` является корнем этого уравнения. Докажем, что других корней нет (и тем самым будет доказана справедливость равенства (12)). Поскольку `x=4` является корнем, многочлен `x^3 — 3x-52` делится на `x-4` без остатка. Выполняя деление, получаем:
$$ {x}^{3}-3x-52=0iff left(x-4right)left({x}^{2}+4x+13right)=0iff left[begin{array}{l}x-4=0,\ {x}^{2}+4x+13=0.end{array}right.$$
У квадратного трёхчлена `x^2 +4x+13` отрицательный дискриминант, поэтому уравнение (13) имеет ровно один корень `x=4`.
При каких `a` и `b` многочлен `F(x)=x^4 +ax^3 — 2x^2 +19x+b` делится на многочлен `x^2 -3x+2`?
1-й способ. Выполним деление с остатком:
Приравниваем коэффициенты остатка к нулю
$$ left{begin{array}{l}7a+28=0,\ b-6a-10=0,end{array}right.iff left{begin{array}{l}a=-4,\ b=-14.end{array}right.$$
2-й способ. `x^2 -3x+2=(x-1)(x-2)`.
Многочлен делится на `(x-1)(x-2)` тогда и только тогда, когда `x=1` и `x=2` являются корнями многочлена. То есть,
$$ begin{array}{c}Fleft(1right)=1+a-2+19+b=0, \ Fleft(2right)=16+8a-8+38+b=0,end{array}iff left{begin{array}{l}18+a+b=0,\ 46+8a+b=0,end{array}right.iff left{begin{array}{l}a=-4,\ b=-14.end{array}right.phantom{rule{0ex}{0ex}}$$
`a=-4`, `b=-14`.
Определение
комплексных чисел и общее правило
арифметических действий над ними
z1
+ z2
= z2
+ z1.
z1
+ (z2
+ z3)
= (z1
+ z2)
+ z3.
(Д2.47)
Сопряженные
комплексные числа. Деление кч
Д
ва
комплексных числа z=x+iy
и z=x-iy
отличающиеся
л
ишь
знаком мнимой части, называются
сопряженными
геометрическое
изображение комплексных чисел

М
одуль
и аргумент КЧ
Алгебраическая,
тригонометрическая и показательная
формы КЧ

Ф
ормула
Муавра,извлечение корня из КЧ
Формула
Муавра
для комплексных чисел
,
заданная в тригонометрической форме
— формула
для
любого
Формула
Муавра сразу следует из формулы
Эйлера
и
правила для экспонент
,
верного, если b
— целое
число.
(Если b
— не целое, то
—
многозначная
функция
переменной a
и
—
одно из её значений.)
Открыта
французским математиком Абрахамом
де Муавром.
Аналогичная
формула применима также и при вычислении
корней n-ой
степени из ненулевого комплексного
числа:
Отметим,
что корни n-й
степени из комплексного числа всегда
существуют, и их количество равно n.
На комплексной плоскости, как видно из
формулы, все эти корни являются вершинами
правильного n-угольника,
вписанного в окружность радиуса
с
центром в точке 0.
Деление многочлена с остатком, теорема Безу
Деление
многочлена
Пусть
P(x) и Q(x) — заданные многочлены и степень
многочлена P(x) больше или равна степени
многочлена Q(x). Если оказывается, что
многочлен P(x) не делится (нацело) на
многочлен Q(x), т.е. не существует многочлена
G(x) такого, что P(x)=Q(x)G(x), то вводят операцию
деления многочлена с остатком.
Разделить
многочлен P(x) на многочлен Q(x) с остатком
— это значит найти два многочлена G(x) и
R(x) таких, что
P(x)=Q(x)G(x)+R(x),
Причем
степень многочлена R(x) меньше степени
многочлена Q(x).
Многочлен
P(x) называется делимым, Q(x) — делителем,
G(x) — частным, R(x) — остатком. При делении
многочлена P(x) на многочлен Q(x) многочлены
G(x) и R(x) находятся однозначно.
Теорема.
Для любых двух многочленов P(x) и Q(x) ╪ 0
частное и остаток от деления P(x) на Q(x)
существуют и единственны.
Т.
Безу.
Остатком при делении многочлена
f(x) из на линейный многочлен (x-c) является
константа f(c).
Док-во:
При делении
f(x) на (x-c) получим:
f(x)=q(x)(x-c)+r.
Полагая
x=c получим:
f(с)=q(с)(с-c)+r=r.
Схема
Горнера
Если
то
при делении f(x)
на g(x)
частное q(x)
имеет вид
где
Остаток
r
находится по формуле
a[0]=q[0]
a[1]=q[1]-q[0]c
a[2]=q[2]-q[1]c
…
a[n-1]=q[n-1]-q[n-2]c
a[n]=r-q[n-1]c
откуда:
q[0]=a[0]
q[1]=a[1]+q[0]c
q[2]=a[2]+q[1]c
…
q[n-1]=a[n-1]+q[n-2]c
r=a[n]+q[n-1]c.
Основная
теорема Алгебры. Разложение на множители
многочлена с компл и действ коэфф
Всякий отличный
от константы многочлен
с комплексными
коэффициентами имеет по крайней мере
один корень
в поле
комплексных чисел. или
Поле комплексных
чисел алгебраически
замкнуто.
Разложение
многочлена степени n
на множители
Многочлен
f(x) с комплексными коэффициентами
Здесь
—
различные корни многочлена кратностей
соответственно
Многочлен f(x) с
действительными коэффициентами
Здесь
—
различные действительные корни
многочлена, кратностей
соответственно
—
различные пары действительных чисел,
удовлетворяющих неравенствам
(каждый
множитель
можно
представить в виде
где
—
пара сопряженных комплексных корней
кратности
).
Признак взаимно
простых многочленов
Для того, чтобы
многочлены f(x) и g(x) из F[x] были взаимно
простыми, необходимо и достаточно,
чтобы в F[x] существовали такие u(x) и v(x),
что u(x)f(x)+v(x)g(x)=1.
Док-во:
— Необходимость:
очевидно.
— Достаточность: Пусть d(x)
— НОД многочленов f(x) и g(x). Значит каждое
из слагаемых левой части делится на
d(x). А значит и правая часть делится на
d(x). Следовательно d(x) — ненулевая
константа.
Рациональные
дроби и разложение их на простейшие
методом неопределённых коэффициентов
Рациональная
дробь — это
число, представленное в виде дроби,
например a / b, где a — числитель, b —
знаменатель. A и B могут представлять
собой целые числа, а также переменные.
Классическим
примером применения метода неопределённых
коэффициентов является разложение
правильной рациональной
дроби
в комплексной
или вещественной
области на элементарные
дроби.
Пусть
p(z)
и q(z)
— многочлены
с комплексными коэффициентами, причём
степень многочлена p(z)
меньше степени многочлена q(z),
коэффициент при старшем члене многочлена
q(z)
равен 1, zi
―
корни многочлена q(z)
с кратностями αi,
следовательно,
Функция
p
/ q
представима, и притом единственным
образом, в виде суммы элементарных
дробей
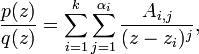
где
Ai,j
― неизвестные пока комплексные числа
(их число равно степени q).
Для их отыскания обе части равенства
приводят к общему знаменателю. После
его отбрасывания и приведения в правой
части подобных членов получается
равенство, которое сводится к системе
линейных уравнений
относительно Ai,j.
Примечание.
Нахождение неизвестных можно упростить,
если q(z)
имеет некратные корни zj.
После умножения на z
− zj
последнего равенства и подстановки z
= zj
непосредственно получаем значение
соответствующего коэффициента
.
Матрицы
и действия над ними

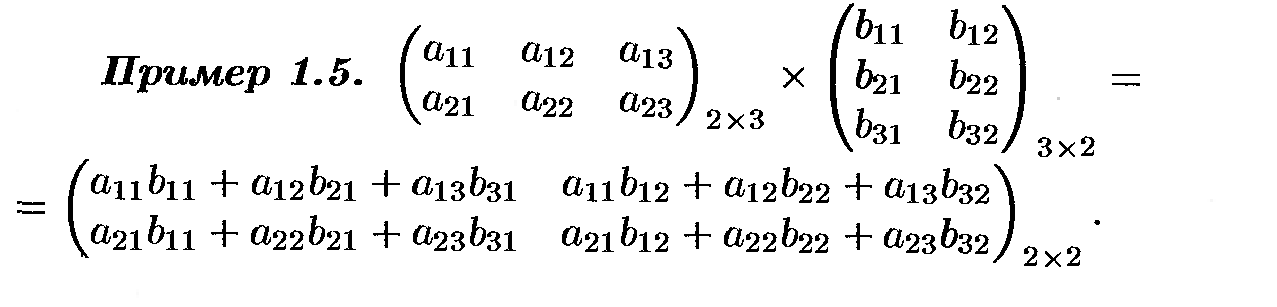

О
пределители
2, 3 и n-го
порядка
М
инором
Mij
элемента aij
(i,j=1,n) называется определитель (n-1)-го
порядка, полученный из определителя
n-го порядка, вычерчиванием i-й строки
и j-го столбца. Алгебраическое дополнение
Aij элемента Aij определяется равенством
Aij=(-1)i+j
Mij
Для
произвольного натурального числа
(теорема Лапласа, разложение по i-строке)
Пример
Для определителя III-го порядка (при
i = 1):
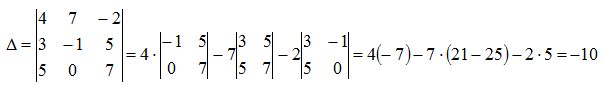
для
определителя IV-го порядка:
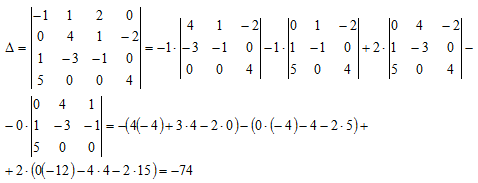
С
войства
определителей

Разложение
определителя по строке или столбцу
По
элементам i-й
строки:
По
элементам j-го
столбца:
Например,
при n = 4
разложение по первой строке
Определитель
произведения матриц
О
пределитель
матрицы
равен
нулю, если
,
и равен сумме попарных произведений
соответствующих друг другу миноров
порядка
,
если
(сумма
берется по всем наборам столбцов матрицы
и
строк матрицы
с
возрастающими номерами
).
Пусть
Т
огда
и
соответствующие миноры имеют вид
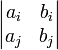
при
всех i
< j,
принимающих значения от 1 до n.
Ф
ормула
Бине — Коши в этом случае дает равенство
и
з
которого (в случае, когда все ai
и bi
являются вещественными числами) вытекает
неравенство
Коши — Буняковского:
Формула
Крамера для решения системы линейных
уравнений

Обратная
матрица и ее вычисление
Свойства
обратной матрицы и новый вывод формул
Крамера
1.
Определитель обратной матрицы обратно
пропорционален определителю начальной
матрицы
.
(4.1.1)
Д
о к а з а т е л ь с т в о :
А-1А
= E, следовательно,
,
а отсюда следует (4.1.1).
2.
Обратная матрица произведения двух
матриц равна произведению обратных
матриц сомножителей, взятых в обратном
порядке
(АВ)-1
=
В-1А-1.
(4.1.2)
Д
о к а з а т е л ь с т в о :
АВ(В-1А-1)
= А(ВВ-1)А-1
=
АЕА-1
=
АА
= Е
и
В-1А-1(АВ)
= В-1(А-1А)В
= В-1ЕВ
= В-1В
= Е.
Следовательно,
по определению (2.1) В-1А-1
— обратная матрица для АВ.
3.
Транспонированная обратная матрица
равна обратной транспонированной
матрице
(А-1)
=
(А)-1.
(4.1.3)
Д
о к а з а т е л ь с т в о :
По
определению (2.1) А-1А
= Е, тогда
(А-1А)
=
А(А-1)
=Е
=
Е.
Умножим
это равенство на (А/)-1:
(А)-1А(А-1)
=
(А)-1Е,
следовательно,
(А-1)
=
(А)-1.
Соседние файлы в предмете Алгебра и геометрия
- #
- #
- #
- #