Алгоритм Форда-Фалкерсона
Время на прочтение
3 мин
Количество просмотров 42K
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
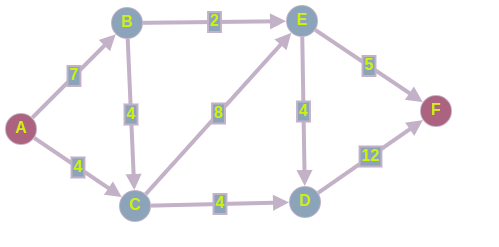
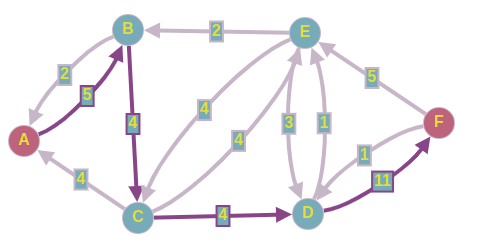
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток
.
Как работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
-
Отправлять определенное количество потока из текущей вершины в соседние.
-
Возвращать определенное количество потока из соседних вершин в текущую.
-
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
-
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
-
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
-
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
-
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
-
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
-
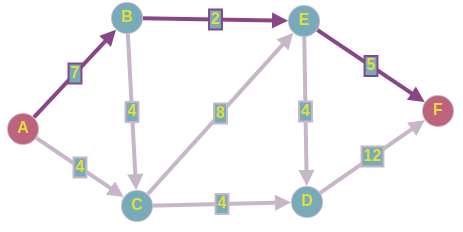
Допустим наш алгоритм нашел следующий путь из вершины
в
нашей остаточной сети, которая на момент начала, совпадает с исходным графом.
-
Сколько потока можем провести по этому пути???
— Больше2 ед.мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в
.
-
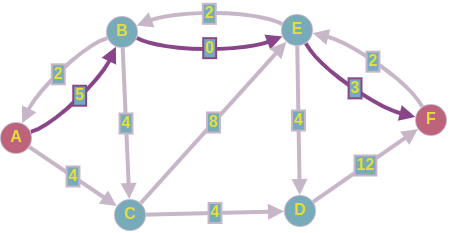
Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:
Пропускаем 3 ед. потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:
-
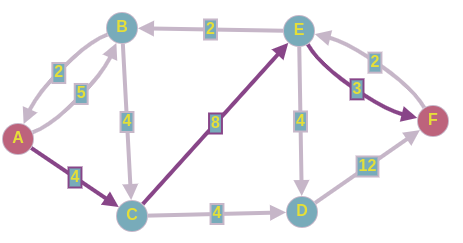
На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:
Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
-
На 4-ой итерации находим следующий путь в остаточной сети:
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Источники
-
Паша и Алгосы
-
Инструмент для работы с графами
Поток минимальной стоимости
Рассмотрим ориентированный граф $G = (V, E)$ с истоком $s$ и стоком $t$, в котором у каждого ребра $(u, v)$ задана целая стоимость $w_{uv}$ и целая положительная пропускная способность $c_{uv}$. Требуется найти максимальный поток, стоимость которого минимальна:
$$ sum_{(u, v) in E} f_{uv} to max $$
$$ sum_{(u, v) in E} f_{uv} w_{uv} to min $$
Заметим, что рёбра отрицательной стоимости по условию возможны. Мы дополнительно предполагаем, что циклов отрицательного веса нет.
Модифицируем сеть, добавив стандартным образом обратные рёбра, позволяющие «отменять» операции: для каждого ребра $(u, v)$ добавим $(v, u)$, для которого $c_{vu} = 0$ и $w_{vu} = -w_{uv}$. Напомним, что остаточной сетью называется граф из рёбер, остаточная пропускная способность которых ненулевая ($c_{uv}-f_{uv} > 0$).
Критерий оптимальности
Если в остаточной сети нет циклов отрицательного веса, то поток оптимален (и наоборот).
Доказательство:
$rightarrow$ Рассмотрим произвольный неоптимальный поток $f$ и оптимальный поток $f^$. Рассмотрим разность $f^-f$. Она является циркуляцией, а любая циркуляция может быть разложена на сумму простых циклов. Хотя бы один из этих циклов будет иметь отрицательную стоимость, так как стоимость $f^*$ меньше стоимости $f$, что противоречит предположению.
$leftarrow$ Пусть цикл существует, тогда мы можем пропустить поток по этому циклу и получить поток меньшей стоимости.
Отмена циклов
Этот критерий сразу даёт нам относительно простой алгоритм: найдем какой-нибудь максимальный поток и будем «отменять» циклы отрицательного веса в остаточной цепи, пока такие циклы существуют. Искать цикл нам придётся не более $mUC$ раз где $U$ — величина потока, $C$ — максимальная пропускная способность ребра. Этой величиной ограничен модуль минимальной стоимости ответа, а каждый отмененный цикл уменьшает ответ хотя бы на единицу.
Если искать цикл алгоритмом Форда-Беллмана, то асимптотика алгоритма составит $O(m^2nUC)$ (предполагая, что какой-нибудь максимальный поток мы уже нашли).
Дополняющие пути
Вспомним общий алгоритм поиска максимального потока, основанный на теореме Форда-Фалкерсона: найти какой-нибудь дополняющий путь, пропустить по нему поток и модифицировать сеть, снова найти дополняющий путь и так далее, пока путь из истока в сток существует. Что будет, если мы каждый раз будем искать не произвольный путь, а путь минимальной стоимости? Утверждается, что такой алгоритм найдет максимальный поток минимальной стоимости.
Утверждение. Алгоритм не создает в остаточной сети циклов отрицательного веса.
Изначально в остаточной сети нет циклов отрицательного веса. Мы нашли минимальный путь из $s$ в $t$ и модифицировали сеть, возможно добавив какие-то обратные рёбра. Могли ли из-за этих рёбер появиться циклы отрицательного веса? Пусть какое-нибудь обратное ребро $(v, u)$ находится в цикле отрицательного веса. Тогда есть путь Из $u$ в $v$ стоимости меньше, чем $w_{uv}$. Но такое не могло произойти: если бы такой путь существовал, то на этапе поиска дополняющего пути мы выбрали бы его вместо ребра $(u, v)$.
Для поиска дополняющего пути можно использовать алгоритм Форда-Беллмана. Асимптотика в данном случае составит $O(nmU)$ — искать каждый дополняющий путь мы будем не более $U$ раз.
Почему мы не использовали алгоритм Дейкстры? Проблема в рёбрах отрицательного веса. Даже если в исходном графе их нет, они могут в процессе алгоритма появиться как обратные. Покажем, как изменить веса рёбер так, чтобы они стали неотрицательными, но информация о кратчайших путях не утратилась: это можно сделать, если дать каждой вершине так называемый «потенциал», который будет учитываться при пересчете стоимостей ребер.
Потенциалы Джонсона
Потенциалом вершины $v$ будем называть расстояние $d_v$ от вершины $s$. Рассмотрим граф из всех достижимых вершин и тех же рёбер, только с изменёнными весами:
$$ w_{uv}’ = w_{uv} + d_u — d_v $$
Утверждение 1. Веса всех рёбер графа неотрицательные.
Доказательство. Пусть вес какого-то ребра $(u, v)$ отрицателен, то есть $w_{uv}’ = w_{uv} + d_u — d_v < 0$. Тогда $d_u + w_{uv} < d_v$, и нарушилось неравенство треугольника: почему мы тогда не использовали ребро $(u, v)$, когда искали кратчайший путь до $v$?
Аналогично можно показать, что рёбра на кратчайших путях из $s$ имеют нулевую стоимость. Заметим, что стоимость обратных рёбер на кратчайших путях тоже будет нулевой:
$$ w_{vu}’ = w_{vu} + d_v — d_u = -w_{uv} — d_u + d_v = -(w_{uv}) = 0 $$
Утверждение 2. Кратчайшие пути между любыми вершинами остались кратчайшими.
Доказательство. Распишем новую стоимость пути из $a$ в $z$.
$$
begin{aligned}
w_{ab}’ + ldots + w_{yz}’
&= (w_{ab} + ldots + w_{yz}) + (d_a + ldots + d_y) — (d_b + ldots + d_z)
&= (w_{ab} + ldots + w_{yz}) + d_a — d_z
end{aligned}
$$
Получаем, что стоимость всех путей из $a$ в $z$ лишь изменилась на константу.
Более того, если мы добавим или удалим некоторые рёбра из графа, потенциалы тоже никак не повлияют на кратчайшие пути.
Заметьте, что в доказательстве мы не использовали то, что $d_v$ — кратчайшие расстояния. Это вообще могут быть произвольные числа.
Утверждение 3. Когда мы проталкиваем поток вдоль кратчайшего пути, удаляя ребра и возможно добавляя обратные, веса в изменённом графе тоже остались корректными (все рёбра неотрицательного веса и все кратчайшие пути остались кратчайшими).
Доказательство. Все добавленные обратные рёбра на кратчайшем пути будут иметь нулевую стомость (утверждение 1), а добавления или удаления рёбер на кратчайшие пути не повлияли (утверждение 2).
Итоговый алгоритм
- Модифицируем сеть, добавив обратные рёбра.
- Если в исходном графе есть рёбра отрицательного веса (но нет циклов отрицательного веса), то посчитать изначальные потенциалы (расстояния) алгоритмом Форда-Беллмана. Иначе достаточно положить потенциалы изначально равными нулю.
- Пока максимальный поток не найден:
-
- Посчитать алгоритмом Дейкстры кратчайшие расстояния от $s$, используя для веса формулу с потенциалами, записать их в $d$.
-
- Протолкнуть максимально возможный поток вдоль кратчайшего пути $s leadsto t$, обновить остаточную сеть.
Реализация
Ниже приведено решение задачи о назначениях (паросочетание минимального веса). Для нахождения дополняющего пути используется алгоритм Дейкстры для плотных графов (без приоритетной очереди — каждую итерацию ищется минимум за $O(n)$).
-
cost,cap— параметры сети -
pot— потенциалы -
par— предок вершины в алгоритме Дейкстры (нужен для проталкивания потока) -
d— временный массив для алгоритма Дейкстры, куда будут записаны новые расстояния
const int maxn = 305, inf = 1e9; int n; int cost[maxn][maxn], cap[maxn][maxn]; int d[maxn], pot[maxn], par[maxn]; bool dijkstra (int s, int t) { used[maxn] = {0}; fill(d, d+n, inf); d[s] = 0; while (1) { int v = -1; for (int u = 0; u < n; u++) if (!used[u] && (v == -1 && d[u] < d[v])) v = u; if (v == -1 || d[v] == inf) break; used[v] = 1; for (int u = 0; u < n; u++) { int w = cost[v][u] + pot[v] - pot[u]; if (cap[v][u] && d[u] > d[v] + w) { d[u] = d[v] + w; par[u] = v; } } } return d[t] < inf; } int mincost_maxflow (int s, int t) { int ans = 0; while (dijkstra(s, t)) { memcpy(pot, d, sizeof(d)); int delta = inf; for (int v = t; v != s; v = par[v]) delta = min(delta, cap[par[v]][v]); for (int v = t; v != s; v = par[v]) { cap[par[v]][v] -= delta; cap[v][par[v]] += delta; ans += cost[par[v]][v]*delta; } } return ans; }
Асимптотика
В общем случае, алгоритм работает за $O(U m log n)$ или $O(U n^2)$ в случае плотных графов.
В наиболее популярных задачах рёбра обычно с единичной пропускной способностью, и $U leq n$ или $U leq m$. Например, в задаче о назначениях $U = n$, и алгоритм работает за $O(n^3)$, что совпадает с асимптотикой венгерского алгоритма.
Представим, что у нас есть диграф и две вершины — источник и сток. У каждого ребра есть вес, который называется его пропускной способностью. Нам нужно пропустить как можно больше материала через диграф от источника к стоку. Это называется потоком, а взвешенный диграф — сетью. Таким образом мы строим сетевой поток.
Например, источник — это
, а сток —
:

Первое число, выделенное красным на каждом ребре — это значение потока, а второе — пропускная способность. В этом случае поток не оптимальный, так как через сеть можно пропустить больше вещей, чем
единиц.
Количество потока на ребре не может превышать его пропускную способность. Еще общее количество потока в вершину должно быть равно общему количеству потока из этой вершины, за исключением источника и стока. В итоге поток проходит через вершины, которые не создают и не потребляют поток.
Общее объем потока, который проходит через сеть, называется величиной потока. Это количество можно найти, если посчитать:
-
Общий поток, который выходит из источника
-
Общий поток, который входит в сток
Многие реальные проблемы можно смоделировать с помощью сетей потоков. Например, источник — это место, где мы добываем сырье. Его нужно доставить на завод — сток. Края — это различные маршруты, по которым мы можем отправить сырье, а мощность — сколько материала можно доставить по этим маршрутам.
Если предположить, что транспортная сеть — это ограничивающий фактор, то нас интересует, сколько сырья мы можем доставить на фабрику.
Многие несвязанные проблемы теории графов можно преобразовать в проблемы сетевых потоков.
Алгоритм Форда-Фалкерсона
Подготовительный
этап.
Выбираем произвольный
поток. В качестве начального потока
можно взять нулевой поток:
для любой дуги
.
Помечаем
источник s:
(эта метка означает, что мы пытаемся
пропустить через сеть бесконечный по
величине поток). Теперь источник
помечен, но не просмотрен. Остальные
вершины не помечены.
Этап
расстановки пометок.
Выбираем
произвольную помеченную и непросмотренную
вершину i
(например, вершину, имеющую минимальный
номер) и пытаемся пометить все смежные
с ней непомеченные вершины j:
все
те вершины j,
для которых
,
получают метку
,
где
;
такие узлыj
теперь помечены и непросмотрены;
все
те вершины j,
для которых
,
получают метку
,
где
;
такие узлыj
теперь помечены и непросмотрены.
После
этой процедуры вершина i
считается
помеченной и просмотренной и больше не
рассматривается на этом шаге даже в
случае, если не все смежные с ней вершины
удалось пометить.
Далее
просматриваем следующую вершину, и так
до тех пор, пока не пометим сток t
или же пока нельзя будет больше пометить
ни одной вершины, при этом сток останется
не помеченным. Если сток окажется не
помеченным, то процесс нахождения
максимального потока в сети можно
считать законченным, а если сток помечен,
то переходим к следующему этапу.
Если
максимальный поток найден, то все
вершины, которые удалось пометить на
этом этапе и вершина s
образуют множество X
и определяют минимальный разрез
.
величины.
Отметим, что все дуги
разреза
такие,что
,
являются насыщенными, а по остальным
дугам разреза «течет» нулевой поток.
Этап
изменения потока.
Используя
первую часть метки вершины, определяем
путь, по которому мы пришли из вершины
s
в вершину t.
Выделение этого пути начинаем с вершины
t:
если вершина t
имеет метку
,
то вершинаt
помечена из вершины i
и т.д. В результате мы получаем
последовательность смежных вершин:
.
По всем дугам
этого пути , начальная вершина которых
имеет пометку «+», увеличиваем поток
на величину
,
а по всем остальным дугам
этого пути , начальная вершина их имеет
пометку «-», уменьшаем поток на эту же
величину
«направление» дуги на этом пути совпадает
с направлением пути. В результате −
поток по сети увеличится на величину
.
После
изменения потока все метки вершин, кроме
метки вершины s
, удаляются и возвращаемся на этап
расстановки пометок.
Конец работы
алгоритма.
3.Пример решения задачи о максимальном потоке и минимальном разрезе
Рассмотрим
конкретную задачу о нахождении
максимального потока в сети.
Дана
сеть G(V,E)
(рис.1) с источником s
и стоком t.
Пропускные способности дуг указаны.
Найти максимальный поток из s
в t.
Рис.1
Решение.
Подготовительный
этап.
М(s)=(s,
+∞); все дуговые потоки нулевые −
для любой дуги
.
Вершина
s
помечена и не просмотрена, остальные
вершины не помечены.
Этап расстановки
пометок
Рассматриваем
вершину s:
М(1)=(,10);
М(2)=(,8)
Вершина
s
помечена и просмотрена, вершины 1, 2
помечены и непросмотрены.
Рассматриваем
вершину 1:
М(3)=(1,
5)
Вершина
1 помечена и просмотрена.
Рассматриваем
вершину 2:
М(4)=(2,

Вершина
2 помечена и просмотрена.
Рассматриваем
вершину 3:
М(t)=(3,
5)
Помечена
вершина t,
переходим
на следующий этап.
Этап изменения
потока
=5
Путь,
по которому мы пришли из вершины s
в вершину t:
(,1
,3
,
t)
Величина
потока r
= 5.
Рис.2
В
прямоугольниках (рис.2) указаны дуговые
потоки после этого этапа, все остальные
дуговые потоки равны нулю.
Этап расстановки
пометок
Рассматриваем
вершину s:
М(1)=(,5);
М(2)=(,8)
Вершина
s
помечена и просмотрена, вершины 1, 2
помечены и непросмотрены.
Рассматриваем
вершину 1:
Вершину 3 из вершины
1 пометить нельзя.
Вершина
1 помечена и просмотрена.
Рассматриваем
вершину 2:
М(4)=(2,

Вершина
2 помечена и просмотрена.
Рассматриваем
вершину 4:
М(t)=(4,

Вершина
4 помечена и просмотрена. Пометили
вершину
t.
Этап изменения
потока
=8
Путь,
по которому мы пришли из вершины s
в вершину t:
(,2
,4
,t)
Величина
потока r
= r+8=13.
Рис.3
Дуговые
потоки после этого этапа указаны на
рис.3, все остальные дуговые потоки равны
нулю.
Этап расстановки
пометок
Рассматриваем
вершину s:
М(1)=(,5)
Вершину
2 из вершины s
пометить нельзя.
Вершина
s
помечена и просмотрена, вершина 1 помечена
и непросмотрена.
Рассматриваем
вершину 1.
М(2)=(,5)
Вершины
3 и 4 из вершины 1 пометить нельзя.
Вершина
1 помечена и просмотрена, вершина 2
помечена и непросмотрена.
Рассматриваем
вершину 2.
М(4)=(2,
2)
Вершина
2 помечена и просмотрена, вершина 4
помечена и непросмотрена.
Рассматриваем
вершину 4.
М(t)=(4,
2)
Вершину 3 из вершины
1 пометить нельзя.
Вершина
4 помечена и просмотрена. Пометили
вершину t.
Этап изменения
потока
=2
Путь,
по которому мы пришли из вершины s
в вершину t:
(,
1,
2,4
,t)
Величина
потока r
= r+2=15.
Рис.4
Дуговые
потоки после этого этапа указаны на
рис.4, все остальные дуговые потоки равны
нулю.
Этап расстановки
пометок
Рассматриваем
вершину s:
М(1)=(,3)
Вершину
2 из вершины s
пометить нельзя.
Вершина
s
помечена и просмотрена, вершина 1 помечена
и непросмотрена.
Рассматриваем
вершину 1.
М(2)=(,
3)
Вершины 3 и 4 из
вершины 1 пометить нельзя.
Вершина
1 помечена и просмотрена, вершина 2
помечена и непросмотрена.
Рассматриваем
вершину 2.
Из вершины 2 других
вершин пометить не удается.
На
этом этапе других вершин пометить не
удалось, следовательно максимальный
поток найден r=15,
а минимальный разрез имеет следующий
вид:
=
Задача
о кратчайшем пути.
Пусть
задана
сеть
G
=
с множеством вершинN,
где
,
и множеством дугU,
т.е. задан ориентированный
граф
с n + 1 вершиной,
в
котором
выделены
две
вершины
–
вход
(нулевая
вершина)
и
выход
(вершина
с
номером
n). Для
каждой
дуги
(i; j) задано
число
,называемое
длиной
дуги.
Длиной
пути
называется
сумма
длин
дуг
этого пути (если
длины
дуг
не
заданы,
то
длина
пути
определяется
как
число
дуг
пути, т.е.
).Задача
о кратчайшем пути
состоит в
поиске
минимального
(кратчайшего)
по длине пути
из вершины с номером 0 до вершины с
номером n.
В
дальнейшем
будем
предполагать:1)
сеть не имеет контуров; 2) из вершины с
номером 0 можно попасть (по некоторому
пути) в
любую
другую вершину
сети,
а из любой
вершины
сети можно
попасть
(по некоторому пути) в вершину с номером
n;
3) нулевая вершина не имеет входящих
дуг, а вершина n
не имеет выходящих дуг.
Сеть G
не имеет контуров, поэтому всегда
можно
пронумеровать
вершины
таким
образом,
что
для
любой
дуги
(i, j) имеет
место
соотношение: i<j.
Такая
нумерация
вершин сети называется
правильной.
Если сеть
G
имеет
правильную
нумерацию
(вершин), то кратчайший путь можно найти
алгоритмом
1. В процессе работы этого алгоритма
каждая вершина получает метку
− вершина i
получает метку M(i)
=(j,
), где первая часть метки указывает номер
вершины, из которой помечена вершинаi,
а величина
указывает длину кратчайшего пути из
нулевой вершины в данную вершину.
Алгоритм
1.
Шаг
0: помечаем
нулевую
вершину
− M(0)
= (0,),
где= 0.
Шаг
k, где
:
помечаем
вершину
с номером k меткой M(k)
=(j,
),
где(т.е.
минимум в соотношениидостигается на вершинеj
).
Длина
кратчайшего
пути
равна
.Используя
первую часть метки вершины, двигаемся
в обратном направлении от вершины с
номером n
до вершины с номером 0 и тем самым
определяем путь, по которому мы пришли
из вершины 0 в вершину n.
В результате мы получаем последовательность
вершин:
.
(Такой способ определения пути называетсяметодом
обратного хода.)
Это и есть кратчайший путь.
Рис. 1
На
рисунке
1 приведен
пример
применения
алгоритма
1 для
определения
кратчайшего
пути:
числа
у
дуг
равны
длинам
дуг,
метки вершин
помещены
в
круглые
скобки,
кратчайший
путь
выделен
жирными линиями.
Правильная нумерация
вершин произвольной сети, не имеющей
контуров, определяется алгоритмом 2. В
процессе работы этого алгоритма каждая
вершина получает метку − её номер при
правильной нумерации вершин. Перед
началом работы алгоритма все вершины
не помечены.
Алгоритм 2.
1.Полагаем, что i
= 0. Находим в сети G
вершину, не имеющую входящих дуг, и
присваиваем ей метку i.
2. Если i
= n,
то правильная нумерация вершин найдена,
заменяем исходную нумерацию вершин
правильной − конец работы алгоритма.
В противном случае
полагаем i
= i
+ 1.
3. Находим в сети
G
любую вершину, которая не имеет входящих
дуг, выходящих из помеченных вершин, и
присваиваем ей метку i.
Возвращаемся на шаг 2.
Рис. 2.
На
рисунке
2 приведен
пример
применения
алгоритма
2 для
отыскания правильной нумерации вершин
сети: метки вершин
− номера правильной нумерации помещены
в
круглые
скобки.
Следующий
алгоритм
дает
возможность
определить
кратчайший
путь
в
общем
случае
− при произвольной нумерации вершин.
В процессе работы этого алгоритма каждая
вершина получает метку
− вершина i
получает метку M(i)
=(j,
), где первая часть метки указывает номер
вершины, из которой помечена вершинаi,
а величина
указывает длину некоторого пути из
нулевой вершины в данную вершину. После
завершения работы алгоритма величинабудет равна длине кратчайшего пути из
нулевой вершины в данную вершину.
Алгоритм
3 (алгоритм
Дейкстры).
Шаг
0. Полагаем, что множество вершин Q − это
пустое множество. Помечаем
нулевую
вершину:
M(0)
= (0,),
где= 0, т.е.M(0)
= (0,0). Заносим нулевую вершину в множество
Q. Все остальные вершины получают метку
− M(i)
=(0,
),
т.е.=
(это означает, что вершинаi
помечена из вершины 0 и, предположительно,
находится от нее на бесконечном
расстоянии).
Шаг
1. Для каждой вершины kQ
вычисляем величину

берется
по
всем
вершинам
i таким, что iQ
и в сети имеется дуга (i,k),
и этот
минимум достигается на вершине j).
Среди всех
таких вершин k
выбираем ту, которая имеет минимальную
величину
,
помечаем ее −M(k)
=(j,
)
и заносим в множествоQ.
Подобную
процедуру
повторяем
до
тех
пор,
пока
не
будет
помечена
вершина
n.
Длина
кратчайшего
пути
равна
.
Используя
первую часть метки вершины, находим сам
кратчайший путь методом обратного хода.
Конец работы
алгоритма.
Рис.3.
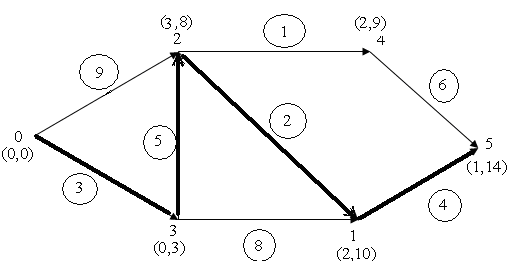
Применим алгоритм
Дейкстры к графу на рис. 3, числа
в кружочках равны
длинам
дуг.
Шаг
0.
M(0) =
(0,0),
M(i) =(0,
)
для
i = 1,2,…,n
Q = {0}
Шаг
1.
;
;
M(3) =(0,
3)
Q = {0, 3}
;
;
M(2) =(3,
8);
Q = {0, 3, 2}
;
;
Q = {0, 3, 2, 4}
;
;
Q = {0, 3, 2, 4, 1}
;
Q = {0, 3, 2, 4, 1, 5}
Рис.4
На
рисунке
4 приведен
пример
применения
алгоритма
1 для
определения
кратчайшего
пути:
числа
у
дуг
равны
длинам
дуг,
метки вершин
помещены
в
круглые
скобки,
кратчайший
путь
выделен
жирными линиями.
Содержание
- 1 Задача о потоке минимальной стоимости
- 1.1 Свойства сети
- 2 Алгоритмы решения
- 2.1 Метод устранения отрицательных циклов в остаточной сети
- 2.1.1 Алгоритм
- 2.1.2 Асимптотика
- 2.2 Метод дополнения потока вдоль путей минимальной стоимости
- 2.3 Использование потенциалов Джонсона
- 2.1 Метод устранения отрицательных циклов в остаточной сети
- 3 См. также
- 4 Источники информации
Задача о потоке минимальной стоимости
| Определение: |
| Пусть дана сеть . — источник и сток. Ребра имееют пропускную способность поток и цену за единицу потока . Тогда общая стоимость потока из в :
|
Свойства сети
- Поток не может превысить пропускную способность.
- Поток из в должен быть противоположным потоку из в .
- Сохранение потока. Для каждой вершины, сумма входящего и исходящего потоков равно .
| Задача: |
| Дана сеть . — источник и сток. Ребра имееют пропускную способность поток — и цену за единицу потока . Требуется найти максимальный поток, суммарная стоимость которого минимальна. |
Алгоритмы решения
Метод устранения отрицательных циклов в остаточной сети
Воспользуемся леммой об эквивалентности свойства потока быть минимальной стоимости и отсутствии отрицательных циклов в остаточной сети. Получим следующий алгоритм:
Алгоритм
- Начало.
- Шаг 1. Определим для каждого прямого ребра обратное ребро . Определим его характеристики: , , .
- Шаг 2. Для каждого ребра зададим поток равный .
- Шаг 3. Найдем произвольный максимальный поток(любым алгоритмом нахождения максимального потока), построим для него остаточную сеть, где каждому ребру будет соответствовать величина .
- Шаг 4. При помощи алгоритма Форда-Беллмана найдем отрицательный цикл в построенной сети (отрицательный цикл ищется по стоимости ребра, т.е. ребра имеют вес ). Если отрицательный цикл не нашелся — перейдем к шагу 6.
- Шаг 5. Избавимся от отрицательного цикла, для этого пустим по нему максимально возможный поток. Величина потока равна минимальной остаточной пропускной способности в цикле. Перейдем к шагу 4.
- Шаг 6. Отрицательных циклов в остаточной сети нет, значит, максимальный поток минимальной стоимости найден.
- Конец.
Асимптотика
Алгоритм Форда-Беллмана работает за , улучшение цикла за . Если обозначить максимальную стоимость потока как , а максимальную пропускную способность как , то алгоритм совершит итераций поиска цикла, если каждое улучшение цикла будет улучшать его на 1. В итоге имеем , где — асимптотика поиска максимального потока.
Метод дополнения потока вдоль путей минимальной стоимости
Использование потенциалов Джонсона
См. также
- Сведение задачи о назначениях к задаче о потоке минимальной стоимости
- Венгерский алгоритм решения задачи о назначениях
Источники информации
- Википедия — Поток минимальной стоимости
- Визуализатор алгоритма нахождения максимального потока минимальной стоимости
- Хабрахабр — Максимальный поток минимальной стоимости
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн Клиффорд Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом «Вильямс», 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)