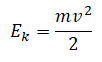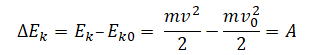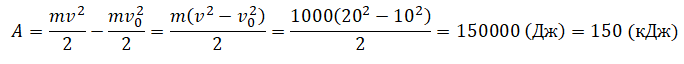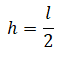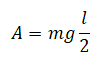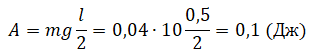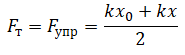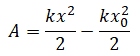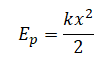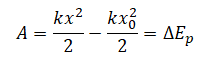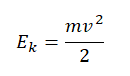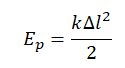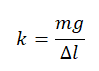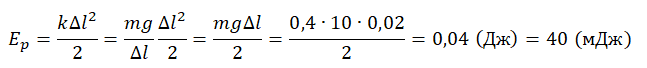В
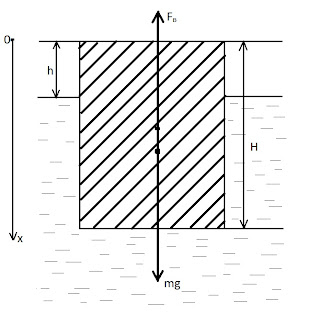
льдине, плавающей в океане, просверлили вертикальный колодец глубиной 10 м.
Какую минимальную работу необходимо затратить для поднятия из этого колодца
ведра с водой массой 10 кг, если плотность льда на 10% меньше воды?
Решение.
Систему
отсчета свяжем с поверхностью Земли и будем считать ее инерциальной. В качестве
физических систем будем рассматривать «льдину» и «ведро с водой –
гравитационное поле Земли».
Обе физические системы являются незамкнутыми, кроме
того, первая из них находится из них относительно выбранной системы отсчета в
состоянии равновесия.
Первую
физическую систему опишем условиями равновесия материальной точки в
инерциальной системе отсчета, вторую – теоремой об изменении механической
энергии.
На
льдину действуют: сила тяжести mg и выталкивающая сила F2 . Поскольку льдина
находится в состоянии равновесия, то имеем.
В
этой записи ρ0 и ρ – плотности воды и льда соответственно. Отсюда
можно найти глубину колодца до поверхности воды в нем.
Минимальная
работа, выполняемая при поднятии ведра с водой, равна изменению его
потенциальной энергии в гравитационном поле Земли.
Нулевой
уровень потенциальной энергии выберем на уровне поверхности воды в колодце,
тогда начальная энергия E1 = 0. Конечная энергия E2 = mgh. Работа, выполненная при поднятии ведра с водой будет равна A.
Численно:
A
= 98 кДж.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Условие задачи:
Какую минимальную работу необходимо совершить, чтобы лежащий на столе груз массой 1 кг поднять на высоту 1 м при помощи привязанного к нему невесомого резинового жгута? В начальном состоянии жгут не растянут, его жесткость 10 Н/м.
Задача №2.8.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=1) кг, (h=1) м, (k=10) Н/м, (A-?)
Решение задачи:
Для начала груз нужно оторвать от стола. Так как груз поднимают резиновым жгутом, то перед тем как груз оторвется от стола, жгут растянется на некоторую величину (x). Как эту деформацию определить? Достаточно записать первый закон Ньютона для покоящегося груза в проекции на ось (y):
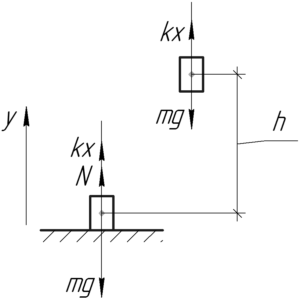
[N + kx – mg = 0]
Здесь (kx) – сила упругости резинового жгута, определяемое по закону Гука:
[{F_{у}} = kx]
Когда груз оторвется от стола, то сила реакции опоры (N) станет равной нулю. Тогда:
[N = 0 Rightarrow kx = mg]
[x = frac{{mg}}{k}]
После отрыва от стола груз поднимают равномерно с такой маленькой скоростью, что ею можно пренебречь, дабы соблюсти условие минимальности работы и не изменить величину деформации жгута (если груз поднимать равноускоренно, то деформация увеличится).
Далее воспользуемся законом сохранения энергии. Согласно ему работа внешней силы есть изменение полной механической энергии системы. В данном случае изменилась потенциальная энергия жгута и груза.
[A = Delta E]
В начале потенциальная энергия обоих тел равна нулю. Когда груз будет поднят на заданную высоту (h), то его потенциальная энергия будет равна ({E_{1}} = mgh), при этом жгут будет растянут на величину (x), а его потенциальная энергия будет равна ({E_{2}} = frac{{k{x^2}}}{2}).
[A = {E_1} + {E_2}]
[A = mgh + frac{{k{x^2}}}{2}]
Так как мы определили, что (x = frac{{mg}}{k}), то:
[A = mgh + frac{k}{2}{left( {frac{{mg}}{k}} right)^2} = mgh + frac{{{m^2}{g^2}}}{{2k}}]
[A = mgleft( {h + frac{{mg}}{{2k}}} right)]
Так как все численные значения величин даны в системе СИ, то можем сразу посчитать ответ:
[A = 1 cdot 10left( {1 + frac{{1 cdot 10}}{{2 cdot 10}}} right) = 15; Дж]
Ответ: 15 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.23 Мяч бросили под углом к горизонту со скоростью 20 м/с. Найти скорость мяча
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.26 Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,984 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Данные задачи: m (масса перемещаемого тела) = 10 кг; тело перемещалось по горизонтальной плоскости; S (требуемое расстояние) = 50 м; μ (коэффициент трения между телом и горизонтальной плоскостью) = 0,5.
Справочные величины: g (ускорение свободного падения) ≈ 10 м/с2.
Минимальную работу силы при перемещении тела можно рассчитать по формуле: A = F * S = Fтр. * S = μ * N * S = μ * m * g * S.
Вычисление: A = 0,5 * 10 * 10 * 50 = 2500 Дж (2,5 кДж).
Ответ: Минимальная работа будет равна 2,5 кДж.
Совершение работы телом не проходит бесследно. Рассмотрим, например, часы с пружинным заводом. При заводе часов состояние системы (часового механизма) меняется так, что она приобретает способность совершать работу в течение длительного времени. Пружина поддерживает движение всех колес, стрелок и маятника, испытывающих сопротивление движению, вызванное трением. По мере хода часов способность пружины совершать работу постепенно утрачивается. Состояние пружины меняется.
Если тело или система тел могут совершить работу, говорят, что они обладает механической энергией.
Определение
Механическая энергия — скалярная физическая величина, являющаяся единой мерой всех форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
Механическая энергия обозначается буквой E. Единица изменения энергии — Джоуль (Дж).
Виды механической энергии
В механике состояние системы определяется положением тел и их скоростями. Поэтому в ней выделяют два вида энергии: потенциальную и кинетическую.
Определение кинетической энергии
Кинетическая энергия — это энергия, которой обладает движущееся тело. Она обозначается как Ek. Кинетическая энергия тела зависит от его массы и скорости. Численно она равна половине произведения массы тела на квадрат его скорости:
Определение потенциальной энергии
Потенциальная энергия — это энергия взаимодействующих тел. Она обозначается как Ep.
Потенциальная энергия в поле тяготения Земли численно равна произведению массы тела на его высоту (расстояние от поверхности планеты) и на ускорение свободного падения:
Ep=mgh
Потенциальная энергия упруго деформированного тела определяется формулой:
Ep=kx22
k — жесткость пружины, x — ее удлинение.
Пример №1. Мальчик подбросил футбольный мяч массой 0,4 кг на высоту 3 м. Определить его потенциальную и кинетическую энергию в верхней точке.
Потенциальная энергия мяча в поле тяготения Земли равна:
Ep = mgh = 0,4∙10∙3 = 12 (Дж)
В верхней точке полета скорость мяча равна нулю. Следовательно, кинетическая энергия мяча в этой точке тоже будет равна нулю:
Ek = 0 (Дж).
Теорема о кинетической энергии
Теорема о кинетической энергии
Изменение кинетической энергии тела равно работе равнодействующей всех сил, действующих на тело:
Эта теорема справедлива независимо от того, какие силы действуют на тело: сила упругости, сила трения или сила тяжести.
Пример №2. Скорость движущегося автомобиля массой 1 т изменилась с 10 м/с до 20 м/с. Чему равна работа равнодействующей силы?
Сначала переведем единицы измерения в СИ: 1 т = 1000 кг. Работа равна изменения кинетической энергии, следовательно:
Работа и потенциальная энергия тела, поднятого над Землей
Величина потенциальной энергии зависит от выбора нулевого уровня энергии. В поле тяготения Земли нулевым уровнем энергии обладает тело, находящееся на поверхности планеты.
Работа силы тяжести
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:
A = – ∆Ep = –(mgh – mgh0) = mg(h0 – h)
Если тело поднимается, сила тяжести совершает отрицательную работу. Если тело падает, сила тяжести совершает положительную работу.
Пример №3. Шарик массой 100 г скатился с горки длиной 2 м, составляющей с горизонталью угол 30о. Определить работу, совершенную силой тяжести.
Сначала переведем единицы измерения в СИ: 100 г = 0,1 кг. Под действием силы тяжести положение тела относительно Земли изменилось на величину, равную высоте горки. Высоту горки мы можем найти, умножим ее длину на синус угла наклона. Начальная высота равна высоте горки, конечная — нулю. Отсюда:
A = mg(h0 – h) = 0,1∙10(2∙sin30o – 0) =2∙0,5 = 1 (Дж)
Потенциальная энергия протяженного тела
Работа силы тяжести
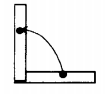
Потенциальная энергия протяженного тела выражается через его центр масс. К примеру, чтобы поднять лом длиной l и массой m, нужно совершить работу равную:
A = mgh
где h — высота центра массы лома над поверхностью Земли. Так как лом однородный по всей длине, его центр масс будет находиться посередине между его концами, или:
Отсюда работа, которую необходимо совершить, чтобы поднять этот лом, будет равна:
Пример №4. Лежавшую на столе линейку длиной 0,5 м ученик поднял за один конец так, что она оказалась в вертикальном положении. Какую минимальную работу совершил ученик, если масса линейки 40 г?
Переведем единицы измерения в СИ: 40 г = 0,04 кг. Минимальная работа, необходимая для поднятия линейки за один конец, равна:
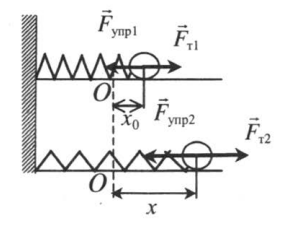
Работа и изменение потенциальной энергии упруго деформированного тела
Вспомним, что работа определяется формулой:
A = Fs cosα
Когда мы сжимаем пружину, шарик перемещается в ту же сторону, в которую направлена сила тяги. Если мы растягиваем ее, шарик перемещается так же в сторону направления силы тяги. Поэтому вектор силы упругости и вектор перемещения сонаправлены, следовательно, угол между ними равен нулю, а его косинус — единице:
Модуль силы тяги равен по модулю силе упругости, поэтому:
Перемещение определяется формулой:
s = x – x0
Следовательно, работа силы тяги по сжатию или растяжению пружины равна:
Но известно, что потенциальная энергия упруго деформированного тела равна:
Следовательно, работа силы, под действием которой растягивается или сжимается пружина, равна изменению ее потенциальной энергии:
Задание EF18117
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Какой из представленных вариантов описания движения соответствует данному графику?
Ответ:
а) Тело брошено под углом к горизонту с поверхности Земли и упало в кузов проезжающего мимо грузовика.
б) Тело брошено под углом к горизонту с поверхности Земли и упало на Землю.
в) Тело брошено под углом к горизонту с поверхности Земли и упало на балкон.
г) Тело брошено вертикально вверх с балкона и упало на Землю.
Алгоритм решения
1.Описать изменение кинетической энергии в течение всего времени движения тела.
2.Установить характер движения тела в течение этого времени.
3.Проанализировать все ситуации и выбрать ту, которая не противоречит установленному характеру движения тела.
Решение
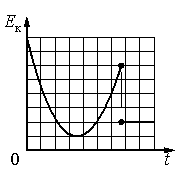
Согласно графику, кинетическая энергия тела сначала уменьшалась, а затем увеличилась. Затем она резко уменьшилась до некоторого значения и осталась постоянной.
Кинетическая энергия тела определяется формулой:
Кинетическая энергия зависит прямо пропорциональной от квадрата скорости. Следовательно, когда уменьшается кинетическая энергия, скорость тоже уменьшается. Когда она возрастает — скорость тоже возрастает. Когда она постоянная — скорость тоже постоянна и не равна нулю.
Если тело брошено под углом к горизонту, скорость сначала будет уменьшаться, так как ускорение свободного падения направлено вниз. Если тело бросить вертикально вверх, скорость тоже сначала будет уменьшаться. Но в этом случае при достижении верхней точки траектории на момент скорость тела будет равна нулю. Следовательно, график зависимости кинетической энергии от времени в этот момент тоже должен быть равен нулю. Но это не так. Поэтому последний вариант ответа не подходит.
Если бы тело упало на неподвижный объект, его скорость относительно Земли стала бы равной нулю. Но так как его кинетическая энергия не равна нулю и является постоянной, тело начало двигаться с постоянной скоростью. Это возможно только в случае, если тело упало на объект, движущийся с постоянной скоростью. Поэтому из всех вариантов ответа подходит только первый, когда тело падает в проезжающий мимо грузовик.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18192
К бруску массой 0,4 кг, лежащему на горизонтальной поверхности стола, прикреплена пружина. Свободный конец пружины тянут медленно в вертикальном направлении (см. рисунок). Определите величину потенциальной энергии, запасённой в пружине к моменту отрыва бруска от поверхности стола, если пружина при этом растягивается на 2 см. Массой пружины пренебречь.
Ответ:
а) 40 мДж
б) 20 мДж
в) 80 мДж
г) 200 мДж
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, указать силы, действующие на пружину, выбрать систему отсчета.
3.Записать формулу для вычисления потенциальной энергии в пружине.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса бруска: m = 4 кг.
• Удлинение пружины: ∆l = 2 см.
Переведем сантиметры в метры:
2 см = 0,02 м
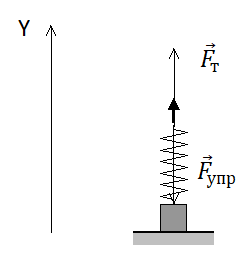
Выполним рисунок. Для описания ситуации нам понадобится только одна ось: Oy.
Потенциальная энергия деформированной пружины определяется формулой:
Так как брусок поднимают за прикрепленную к нему пружину медленно, можно считать, что это движение равномерное (и прямолинейное). Поэтому, согласно второму закону Ньютона:
Fт = Fупр
Чтобы оторвать брусок от поверхности стола, модуль силы тяги должен быть равен модулю силы тяжести. Поэтому:
Fт = Fтяж =Fупр
Или:
mg = k∆l
Теперь можем выразить жесткость пружины:
Подставим жесткость пружины в формулу потенциальной энергии и сделаем вычисления:
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18553
Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t2(все величины выражены в СИ).
Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные и перевести их единицы измерения величин в СИ.
2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.
3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.
4.Определить перемещение тела и его кинетическую энергию.
5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.
Решение
Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.
Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:
x(t)=x0+v0t+at22
Теперь мы можем выделить кинематические характеристики движения тела:
• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).
Перемещение тела определяется формулой:
s=v0t+at22
Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:
x(t)=v0t+at22=5t−3t2
Кинетическая энергия тела определяется формулой:
Ek=mv22
Скорость при прямолинейном равноускоренном движении равна:
v=v0+at=5−6t
Поэтому кинетическая энергия тела равна:
Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2
Следовательно, правильная последовательность цифр в ответе будет: 34.
Ответ: 34
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.6k