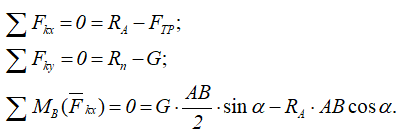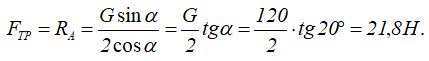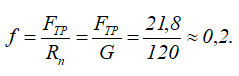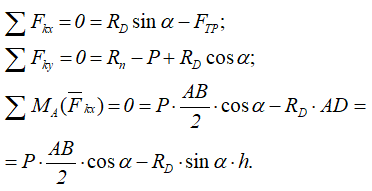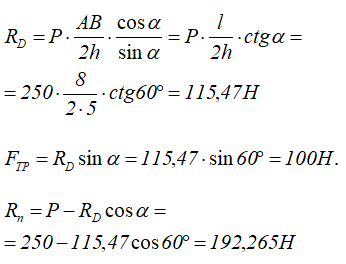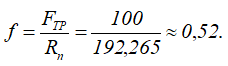Коэффициент трения скольжения

4
Средняя оценка: 4
Всего получено оценок: 100.
4
Средняя оценка: 4
Всего получено оценок: 100.
Физическая величина, характеризующая трущиеся поверхности, называется коэффициентом трения скольжения. Величина обозначается буквой μ. Коэффициент трения определяют опытным путём.
Сила трения скольжения
На покоящиеся и движущиеся тела всегда действуют силы трения. Они возникают при соприкосновении твердых тел, твердых тел и жидкостей или газов и подчиняются законам Ньютона. Направление сил трения противоположно движению тела и силам, стремящимся изменить его положение.
В случае, когда тело движется относительно другого, говоря о трении скольжения. Она зависит от:
- Силы нормальной реакции опоры $vec N$,
- От скорости движения (но в вычислениях этой зависимостью пренебрегают),
- От безразмерного коэффициента трения скольжения $mu$, который характеризует свойства и состояние поверхностей соприкосновения.
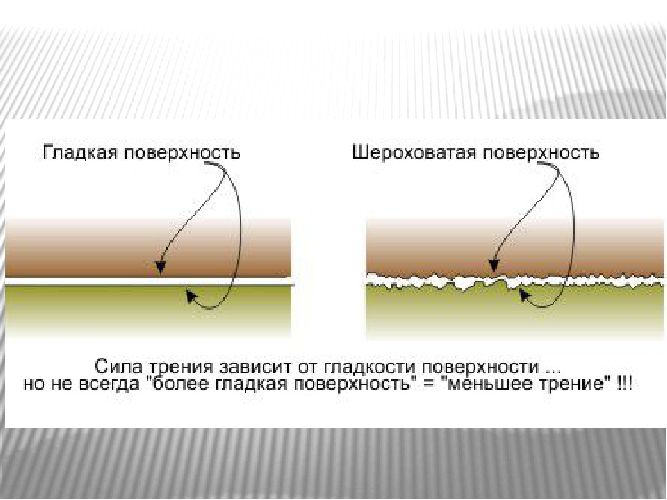
Коэффициент зависит от свойств материала. Чем больше шероховатость поверхности, тем больше значение коэффициента и, соответственно, больше сила трения. Коэффициент трения смазанных поверхностей будет меньше, чем у несмазанных для одной и той же пары материалов. Также коэффициент трения зависит от скорости. Однако эта зависимость минимальна и ей пренебрегают, если не требуется точность измерения. Поэтому коэффициент трения считается постоянным.
Расчет коэффициента трения скольжения
С достаточно большой точностью силу трения скольжения рассчитывают как предельную силу трения покоя по формуле:
$F_{тр} = mu cdot N$.
Тогда формула коэффициента трения скольжения:
$mu ={{F_{тр}} over {N}}$
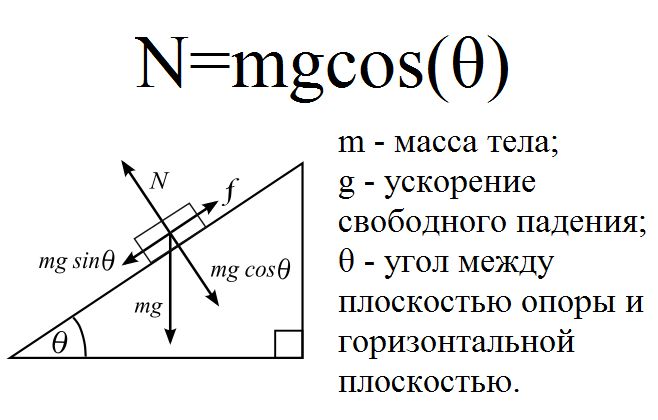
Значение N рассчитывается как произведение массы тела на ускорение свободного падения и на косинус угла к поверхности приложения:
$N = m cdot g cdot cos alpha$
Для большинства пар материалов коэффициент рассчитан опытным путём. Значения находятся в пределах 0,1…0,5. Некоторые значения представлены в таблице.
|
Трущиеся материалы |
Коэффициенты трения |
|
|
Покоя |
При движении |
|
|
Алюминий по алюминию |
0,94 |
|
|
Бронза по бронзе |
0,20 |
|
|
Бронза по чугуну |
0,21 |
|
|
Дерево по дереву |
0,65 |
0,33 |
|
Дерево по камню |
0,46-0,60 |
|
|
Дуб по дубу (вдоль волокон) |
0,62 |
0,48 |
|
Дуб по дубу (перпендикулярно волокнам) |
0,54 |
0,34 |
|
Железо по бронзе |
0,19 |
0,18 |
|
Железо по железу |
0,15 |
0,14 |
|
Железо по чугуну |
0,19 |
0,18 |
|
Каучук по дереву |
0,80 |
0,55 |
|
Каучук по металлу |
0,80 |
0,55 |
|
Кирпич по кирпичу (гладко отшлифованные) |
0,5-0,7 |
|
|
Лёд по льду |
0,028 |
|
|
Медь по чугуну |
0,27 |
|
|
Металл по дереву |
0,60 |
0,40 |
|
Металл по камню |
0,42-0,50 |
|
|
Металл по металлу |
0,18-0,20 |
|
|
Олово по свинцу |
2,25 |
|
|
Полозья деревянные по льду |
0,035 |
|
|
Обитые железом полозья по льду |
0,02 |
|
|
Резина (шина) по твёрдому грунту |
0,40-0,60 |
|
|
Резина (шина) по чугуну |
0,83 |
0,8 |
|
Сталь (коньки) по льду |
0,02-0,03 |
0,015 |
|
Сталь по железу |
0,19 |
|
|
Сталь по стали |
0,15-0,25 |
0,09 при 3 м/с, 0,03 при 27 м/с |
|
Чугун по дубу |
0,65 |
0,30-0,50 |
|
Чугун по стали |
0,33 |
0,13 |
|
Чугун по чугуну |
0,15 |
Коэффициент трения – переменная величина. Поэтому значение коэффициента трения скольжения, приведённые в таблице, являются истинными только при соблюдении определённых условий, в которых были получены.
Что мы узнали?
Коэффициент трения скольжения – физическая величина, характеризующая трущиеся поверхности. Как найти: $mu = {{F_{тр}} over {N}}$. На практике коэффициент рассчитывается исходя из свойств материала эмпирическим путём.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 100.
А какая ваша оценка?

Примеры решения задач по определению коэффициента трения скольжения f между шероховатой горизонтальной поверхностью (полом) и балкой (лестницей), при котором они, опираясь верхним концом о гладкую стену или выступ, будут находиться в состоянии статического равновесия или начнут скользить.
Определение коэффициента трения для равновесия
Задача
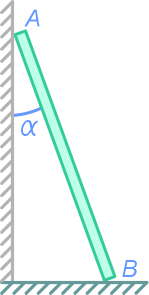
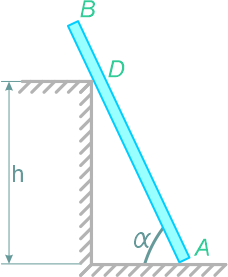
Определить, при каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену.
Вес лестницы G=120 Н, угол между лестницей и стеной α=20°
Другие примеры решений >
Помощь с решением задач >
Решение
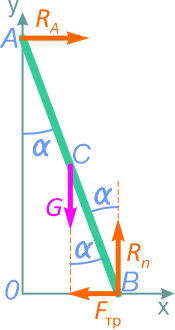
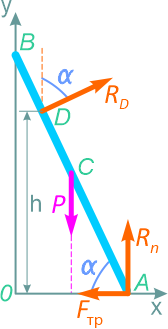
На лестницу действует только одна нагрузка – ее собственный вес, приложенный в точке C посередине длины лестницы AB. Вес лестницы уравновешен реакцией RA гладкой стены и реакцией шероховатого пола, которую заменим двумя составляющими: Rn – нормальной составляющей и FТР – силой трения.
В данном случае, реакция RA будет направлена по нормали к соприкасаемой поверхности.
Составим три уравнения равновесия:
Откуда получаем
Отсюда минимальный коэффициент трения, обеспечивающий равновесие лестницы определяем по формуле
Таким образом, лестница будет находиться в равновесии при f ≥ 0,2.
Расчет коэффициента трения скольжения балки
Задача
Однородная балка весом P и длиной l опирается на шероховатую поверхность и выступ высотой h.
Коэффициент трения балки о пол равен f, угол наклона балки к полу равен α.
Дано: P=250Н, l=8м, h=5м, α=60°.
Требуется найти коэффициент трения f, при котором балка начнет скользить.
Решение
Здесь, реакция RD будет направлена по нормали к соприкасаемой поверхности.
Аналогично предыдущей задаче записываем три уравнения равновесия системы:
Две суммы проекций всех сил на оси x и y, и суммы моментов относительно нижней точки балки.
Из полученных уравнений выражаем и определяем значения составляющих реакций связей
Искомый коэффициент трения f определим из отношения силы трения скольжения к нормальной реакции в точке.
Ответ: для того чтобы балка начала скользить, коэффициент трения скольжения не должен превышать значение f < 0,52
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Минимальное значение — коэффициент — трение
Cтраница 1
Минимальное значение коэффициента трения ( рис. 9) в зоне, где отсутствует взаимное влияние микро-контактов на процессы деформирования материала, объясняется переходом от упругих деформаций на площадках фактического касания в пластические. Минимальный коэффициент трения определяется в зависимости от физико-химического состояния поверхности по формуле ( 91) гл. Контурное давление, соответствующее данному минимальному коэффициенту трения, рассчитывается по формуле ( 89) гл.
[1]
Минимальное значение коэффициента трения при концентрации С0 зависит от длины и линейного строения неполярного углеводородного остатка в молекулах ПАВ и масел. Увеличение трения при дальнейшем увеличении содержания ПАВ и масел на волокне зависит только от вязкости.
[3]
Определить минимальное значение коэффициента трения, при котором это возможно.
[4]
Если минимальные значения коэффициента трения соответствуют восходящей ветви кривой И / 2 ( Ку) — а это области Ку с высокими скоростями изнашивания, то конструкцию следует изменить в направлении сближения значений ( или областей) удельных нагрузок, оптимальных как с точки зрения трения, так и износа. Последнее возможно достигнуть перемещением области У. Перемещение или расширение области оптимальных значений Ку ОПТ Л достигается использованием свойств эластичного материала и особенностей конструкции резинометал-лической пяты.
[5]
Величина минимального значения коэффициента трения при данной конструкции подшипника и данной вязкости практически одинакова для всякого удельного давления.
[6]
Это и есть минимальное значение коэффициента трения, при котором равновесие возможно.
[7]
Каким должно быть минимальное значение коэффициента трения скольжения, чтобы шар катился, а не скользил.
[8]
Наилучшая ориентация пленки и минимальные значения коэффициента трения наблюдаются при трении графита по металлам ( карбидообра-зующим и растворяющим углерод), адгезия к которым максимальна.
[9]
Одновременно можно констатировать, что минимальные значения коэффициентов трения fmin достигаются при тем больших скоростях, чем выше удельные давления.
[10]
Формула ( 2) дает минимальное значение коэффициента трения г, при котором возможно равновесие у наклонной стенки с углом р в отсутствие трения о пол. При этом лестница как бы цепляется за шероховатую стенку, хотя другим концом она, конечно, давит на гладкий пол.
[11]
Формула ( 2) дает минимальное значение коэффициента трения ( А, при котором возможно равновесие у наклонной стенки с углом р в отсутствие трения о пол. При этом лестница как бы цепляется за шероховатую стенку, хотя другим концом она, конечно, давит на гладкий пол.
[12]
Если в спроектированной и исследованной пяте минимальные значения коэффициента трения соответствуют высоким удельным нагрузкам, задача совмещения оптимальных значений Ку опт ц и У. В этом случае следует повысить эластичность резиновой обкладки подпятника, что легко достигается, например, увеличением выступания резины над остовом подпятника. Однако возможности в этом направлении не безграничны. Нужно иметь в виду, что при увеличении эластичности пяты могут увеличиться потери на трение и износ резины.
[13]
Идеальный режим трения характеризуется полным отсутствием износа и минимальными значениями коэффициентов трения.
[15]
Страницы:
1
2
3

{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу
mu = dfrac{F_{тр}}{mg}
Fтр — сила трения
m — масса тела
g — ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона
mu = tg(alpha)
α — угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Трение — это сила, которая противодействует движению. Физики различают статическое трение, которое действует, чтобы удерживать тело в покое, и кинетическое трение, которое замедляет его движение, когда оно начинает двигаться. Сила, создаваемая статическим трением ( F s ), пропорциональна перпендикулярной силе, прикладываемой телом к поверхности, по которой оно движется, что называется нормальной силой ( F N ). Коэффициент пропорциональности называется коэффициентом статической дроби, который обычно обозначается греческой буквой mu с индексом s ( µ s ). Математическое соотношение:
Этот коэффициент зависит от характеристик двух поверхностей, которые находятся в контакте друг с другом. Он был сведен в таблицу для ряда различных материалов. Если вы не можете найти µ s для материалов, которые вы используете, вы можете определить это с помощью простого эксперимента.
TL; DR (слишком долго; не читал)
TL; DR (слишком долго; не читал)
Чтобы найти минимальный коэффициент статического трения между двумя материалами, постройте наклонную плоскость из одного из материалов и поместите на нее корпус, изготовленный из другого материала. Увеличивайте угол наклона, пока тело не начнет скользить. Тангенс угла является коэффициентом трения.
Используйте наклонную плоскость
Простой способ определить µ s — поместить рассматриваемый объект на наклонную плоскость, изготовленную из того же материала, что и поверхность, которую вы изучаете. Постепенно увеличивайте угол наклона, пока объект не начнет скользить. Запишите этот угол. Вы можете сразу найти µ s, потому что он равен тангенсу угла. Вот почему:
Когда вы поднимаете наклон, сила тяжести, действующая на тело массы m, имеет горизонтальную и вертикальную составляющие. Применяя закон Ньютона к каждому из них непосредственно перед тем, как тело начинает двигаться, вы обнаружите, что горизонтальный компонент (который действует в направлении x ) равен F x = ma x . То же самое верно в направлении y : F y = ma y .
Ускорение в направлении x , ma x , равно силе тяжести, которая равна массе, умноженной на ускорение за счет силы тяжести ( g ), умноженной на синус угла ( ø ), образованного в точке опоры наклона. Поскольку тело не движется, это равно противодействующей силе статического трения, и вы можете написать:
(1) мг × грех ( ø ) = F s
Компонент силы y , направления y , равен косинусу угла, умноженного на массу, умноженную на ускорение силы тяжести, и это должно равняться нормальной силе, поскольку тело не движется,
(2) F N = мг × cos ( ø )
Помните, что F s = µ s F N. Заменить на F s в уравнении (1):
и использовать равенство уравнению (2) для замены F N :
mg × sin ( ø ) = µ s × mg × cos ( ø )
Термин « мг » отменяется с обеих сторон:
µ s = sin ( ø ) / cos ( ø ) = tan ( ø )