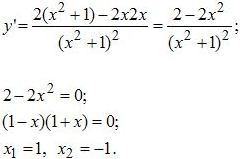Как найти минимальное значение функции через производную - Avtoru.top

Определение

Наибольшим или наименьшим значением функции в определенной области называют наибольшее или наименьшее значение, которое достигает эта функция на указанной области.

Чтобы найти наибольшее или наименьшее значение функции в данной области, нужно решить задачу на экстремум, то есть найти производную заданной функции, приравнять её к нулю и найти точки, в которых производная функции обращается в нуль. Потом из этих точек нужно выбрать только те, которые входят в нашу заданную область. Затем нужно вычислить значение функций в этих точках. Кроме этого, нужно найти значение функции в граничных точках заданной области (если это отрезок) и сравнить их со значениями в точках экстремума. Потом можно сделать вывод о наименьшем или наибольшем значении функции в данной области.

Пример 1

Определить наименьшее и наибольшее значения функции y=x3−6×2+9y=x^3-6x^2+9 на отрезке [−1;2][-1;2].

Решение

Сначала вычисляем производную исходной функции:

y′=3×2−12xy’=3x^2-12x

Затем приравниваем ее к нулевому значению и решаем уравнение:

3×2−12x=03x^2-12x=0

x(3x−12)=0x(3x-12)=0

x1=0x_1=0

x2=4x_2=4

Затем — непосредственный поиск максимального и минимального значений функции на заданном отрезке. Важно отметить, что точка x=4x=4 не входит в заданный отрезок, поэтому значение функции в этой точке вычислять не требуется.

Находим значение функции в точке x1x_1:

f(0)=9f(0)=9

Кроме этого, нужно найти значение функции в граничных точках нашего отрезка, то есть в точках x=−1x=-1 и x=2x=2:

f(−1)=−1−6+9=2f(-1)=-1-6+9=2

f(2)=8−24+9=−7f(2)=8-24+9=-7

Получаем, что на заданном отрезке, наименьшее значение функции, которое равно −7-7, достигается в точке x=2x=2 , а наибольшее значение, равное 99, достигается в точке x=0x=0.

Пример 2

Найти наибольшее и наименьшее значение функции-параболы y=3x2y=3x^2 на всей области её определения.

Решение

Функция y=3x2y=3x^2 определена на всем интервале от минус бесконечности к плюс бесконечности. Найдем производную этой функции:

y′=6xy’=6x

Приравниваем производную к нулю:

6x=06x=0

x=0x=0

Точка x=0x=0 — единственный экстремум этой функции. В этой точке функция равна f(0)=0f(0)=0. Остается решить максимум это или минимум.

Так как график нашей функции это парабола, ветви которой направлены вверх (поскольку 3>03>0), то точка x=0x=0 — точка минимума этой функции. Следовательно, функция y=3x2y=3x^2 достигает своего минимального значения в точке x=0x=0 равного 00. Максимального значения эта функция не имеет. Оно только приближается к сколь угодно большому числу когда значение аргумента стремится к плюс или минус бесконечности.

Тест по теме “Наибольшие и наименьшие значения функции”

Не можешь разобраться в этой теме?

Обратись за помощью к экспертам

Гарантированные бесплатные доработки

Быстрое выполнение от 2 часов

Проверка работы на плагиат

Источник

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим производную функции

3. Приравниваем производную к нулю

4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции $f^{prime}(x)>0$ , то функция y=f(x) возрастает на этом промежутке.

Если на промежутке I производная функции $f^{prime}(x)<0$ , то функция y=f(x) убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: f(0) , а наименьшее — в левом: f(-1) .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума f(0) , а наименьшее — в одном из концов отрезка, то есть надо найти значения f(-1) и f(1) и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть f(0) и f(2) .

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть f(4/3) и f(-1) .

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции — множество действительных чисел.

2. $f^{prime}(x)=3x^2-4x$

3. , если x_1=0 или x_2=4/3

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике

1. Задание B15 (№ 26695)

Найдите наибольшее значение функции на отрезке .

1. Функция определена при всех действительных значениях х

2. $y^{prime}= 15-3cosx$

cosx=5 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

y(0)=5

Ответ: 5.

2. Задание B15 (№ 26702)

Найдите наибольшее значение функции на отрезке [].

1. ОДЗ функции

2. $y^{prime}=3/{cos^2{x}}-3$

Производная равна нулю при , однако, в этих точках она не меняет знак:

$0<cos^2{x}<=1$ , следовательно, $3/{cos^2{x}}>=3$ , значит, $3/{cos^2{x}}-3>=0$ , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция возрастает и принимает наибольшее значение в правом конце промежутка, при x=0 .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

$y^{prime}=3/{cos^2{x}}-3={3-3cos^2{x}}/{cos^2{x}}={3sin^2{x}}/{cos^2{x}}=3tg^2{x}>=0$

у(0)=5

Ответ: 5.

3. Задание B15 (№ 26708)

Найдите наименьшее значение функции на отрезке [].

1. ОДЗ функции :

2. $y^{prime}=2/{cos^2{x}}-4$

3. $2/{cos^2{x}}-4=0$

$cos^2{x}=1/2$ ,

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку принадлежат два числа: -{pi}/4 и {pi}/4

Расставим знаки. Для этого определим знак производной в точке х=0: $y^{prime}(0)=2/{cos^2(0)}-4=-2<0$ . При переходе через точки -{pi}/4 и {pi}/4 производная меняет знак.

Изобразим смену знаков производной функции на координатной прямой:

Очевидно, что точка является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а таковым на является, следовательно подставим в уравнение функции

Ответ: -1

Вероятно, Ваш браузер не поддерживается. Попробуйте скачать

Firefox

И.В. Фельдман, репетитор по математике.

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Простой алгоритм нахождения экстремумов. Учимся находить с bugaga.net.ru.

Находим производную функции
Приравниваем эту производную к нулю
Находим значения переменной получившегося выражения (значения переменной, при которых производная преобразуется в ноль)
Разбиваем этими значениями координатную прямую на промежутки (при этом не нужно забывать о точках разрыва, которые также надо наносить на прямую), все эти точки называются точками «подозрительными» на экстремум
Вычисляем, на каких из этих промежутков производная будет положительной, а на каких – отрицательной. Для этого нужно подставить значение из промежутка в производную.

Из точек, подозрительных на экстремум, надо найти именно экстремумы. Для этого смотрим на наши промежутки на координатной прямой. Если при прохождении через какую-то точку знак производной меняется с плюса на минус, то эта точка будет максимумом, а если с минуса на плюс, то минимумом.

Чтобы найти наибольшее и наименьшее значение функции, нужно вычислить значение функции на концах отрезка и в точках экстремума. Затем выбрать наибольшее и наименьшее значение.

https://bugaga.net.ru/ege/math/ekstremum.html bugaga.net.ru

Рассмотрим пример

Находим производную и приравниваем её к нулю:

Полученные значения переменных наносим на
координатную прямую и высчитываем знак производной на каждом из промежутков. Ну
например, для первого возьмём -2,
тогда производная будет равна -0,24,
для второго возьмём 0, тогда
производная будет 2 , а для третьего возьмём 2, тогда производная будет -0,24. Проставляем соответствующие знаки.

Видим, что при прохождении через точку -1 производная меняет знак с минуса на плюс, то есть это будет точка минимума, а при прохождении через 1 – с плюса на минус, соответственно это точка максимума.

Смотрите также:

Решение ЕГЭ по математике (часть B)
Как найти экстремум (точки максимума и минимума) функции
Формулы логарифмов
Таблица со значениями синусов, косинусов
Таблица производных

Еще больше материалов для подготовки к ЕГЭ

Источник

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Тест по теме “Наибольшие и наименьшие значения функции”

Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Не пропустите также:

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.