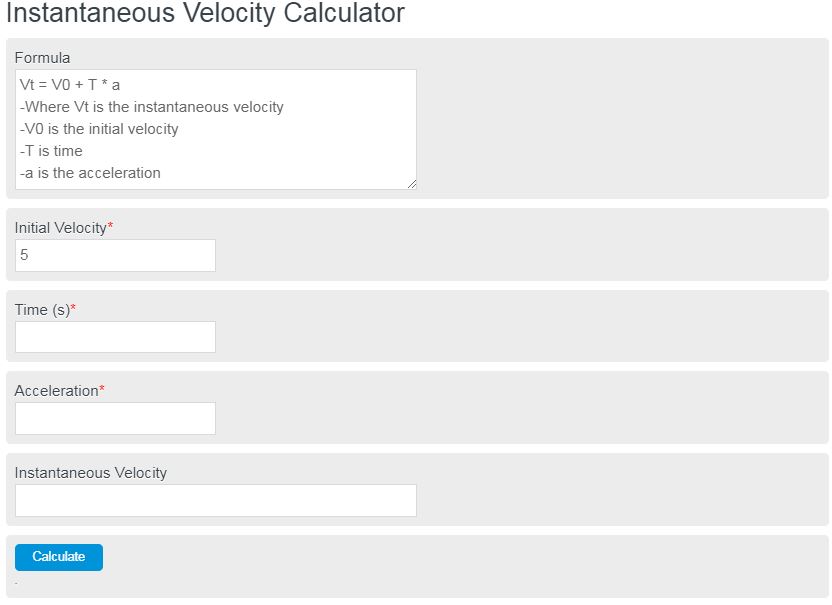
Calculate the instantaneous velocity of an object using this instantaneous velocity calculator. Enter the initial velocity, acceleration, and time past to calculate the velocity at a given time. This calculator can evaluate the initial velocity, time, or acceleration, given the other variables are known.
- All Velocity Calculators
- Acceleration Calculator
- Velocity Calculator
- Angular Acceleration Calculator
- Angular Velocity Calculator
- Final Velocity Calculator
The following formula can be used to calculated the velocity of an object at any given point in time assuming initial time = 0.
- Where Vt is the instantaneous velocity
- V0 is the initial velocity
- T is time
- and a is acceleration
To calculate instantaneous velocity, multiply the acceleration by time, then add the result to the initial velocity.
Instantaneous Velocity Definition
Instantaneous velocity is a term in physics used to describe the velocity, also known as the change in distance over time, at a specific point in time. An object undergoing acceleration will have different instantaneous velocities at different points in time. This is because acceleration is the rate of change of velocity, so that says that velocity is in fact changing.
Instantaneous velocity can be found through two different methods. The first being through calculations and formulas. One of those formulas is presented above. Another formula that you can use is to take the derivative of acceleration with respect to time, at the specific time you wish to calculate the velocity.
The other method to calculate instantaneous velocity is through measurement using things like a speedometer. This is often done for things like measuring the speed of a car or
How to calculate instantaneous Velocity
The following example is a step-by-step guide on how to calculate the instantaneous velocity of an object. For this example, we will assume an object has an initial velocity and some constant acceleration.
- First, we must measure the initial velocity. We will say for this example that this is a car moving along the street. At a time of t=0 seconds, we find the car to be moving at 30 m/s.
- Next, we must determine the acceleration of the car. To simplify the problem, we will assume that we know the acceleration, as calculating it from the force of the engine and other factors would be a problem on its own. We find the acceleration is 5 m/s^2.
- Now, the total time that has passed needs to be determined. For this example, 10 seconds have passed.
- Finally, enter the information into the formula above. V= 30m/s + 10s * 5 m/s^2 = 80m/s.
- Analyze the results and apply them to future problems.
FAQ
What is an instantaneous velocity?
Instantaneous velocity is a term in physics used to describe the velocity, also known as the change in distance over time, at a specific point in time. An object undergoing acceleration will have different instantaneous velocities at different points in time. This is because acceleration is the rate of change of velocity, so that says that velocity is in fact changing.

Скорость, время и ускорение
Расчеты
Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:
V = V0 + а*t
V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.
Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
Если V0 = 0, то V = а*t.
Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.
t = (V — V0) / а
Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:
а = (V — V0) / t
При торможении:
а = (V0 — V) / t
Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).
Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δv, полученный результат делим на разницу между временем Δt.(начальным и конечным) :
а = Δv / Δt
Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.
Расчет скорости, времени и ускорения
Содержание материала
- Советы
- Видео
- Что такое мгновенная скорость на реальных примерах
- Как найти мгновенную скорость из средней скорости
- Мгновенная скорость при криволинейном движении
- Ускорение. Касательное ускорение. Центростремительное ускорение
- Об особенностях понятия мгновенной скорости
- Что мы узнали?
Советы
- Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить производную функции перемещения. Затем возьмите еще раз производную от полученной производной. Это даст вам уравнение для нахождения ускорения в данный момент времени — все, что вам нужно сделать, это подставить значение для времени.
- Уравнение, описывающее зависимость у (перемещение) от x (время), может быть очень простым, например: у = 6x + 3. В этом случае наклон является постоянным и не надо брать производную, чтобы его найти. Согласно теории линейных графиков, их наклон равен коэффициенту при переменной x, то есть в нашем примере =6.
- Перемещение подобно расстоянию, но оно имеет определенное направление, что делает его векторной величиной. Перемещение может быть отрицательным, в то время как расстояние будет только положительным.
Видео
Что такое мгновенная скорость на реальных примерах
Реальные примеры мгновенной скорости
Если мы рассмотрим пример мяча для сквоша, мяч возвращается в исходную точку; в это время полное смещение и средняя скорость будут равны нулю. В таких случаях движение рассчитывается по формуле мгновенная скорость.
Как найти мгновенную скорость из средней скорости
Для того, чтобы найти мгновенная скорость в точке, мы должны сначала найти среднюю скорость в этой точке.
Вы можете найти мгновенную скорость при t = a с помощью вычисление средней скорости графика зависимости положения от времени путем взятия меньшего и большего приращения точки, в которой вы хотите определить Vinst.
Мгновенная скорость при криволинейном движении
Положение материальной точки на траектории зададим радиус-вектором $overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:
скорость — это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.
Единицы измерения ускорения:

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Об особенностях понятия мгновенной скорости
Для того чтобы вычислить мгновенную скорость на практике, следует понимать, что она представляет собой функцию времени. Следует определить на какое расстояние переместился объект в течение крайне малого промежутка времени, который называют моментом времени. Насколько же мал этот допустимый интервал? Если рассматривать совершенные приборы, например радиолокационные станции, то даже самые точные из них позволяют отслеживать скорость за время, которое примерно составляет около 10-6 с. Согласитесь, что несмотря на ничтожную малость этого значения, оно ни в коей мере не является моментом времени, а представляет собой временной промежуток. По этой причине отношение физиков к понятию скорости в определенный момент времени неоднозначное, и оно считается не наделенным конкретным физическим смыслом. Хотя на практике термин «мгновенная скорость» широко используется при управлении навигацией в авиации и космонавтике.
Подобным образом можно рассуждать и о мгновенном ускорении, которое представляет собой зависимость, а точнее производную от скорости и имеет с ней одно направление.
Что касается мгновенной скорости физического тела, находящегося в состоянии покоя относительно выбранной системы отсчета, то она будет равняться нулю.
Что мы узнали?
Мгновенная скорость – это скорость прохождения данного малого участка пути за малый промежуток времени. В идеале мгновенная скорость определяется на текущем бесконечно малом промежутке времени, за который совершается бесконечно малое перемещение.
Теги
Мгновенная скорость, теория и онлайн калькуляторы
Мгновенная скорость
Мгновенная скорость при прямолинейном движении материальной точки
При рассмотрении неравномерного движения часто интересует не средняя скорость движения тела, а скорость в определенный момент времени, или мгновенная скорость. Так, если тело стукнулось о препятствие, то сила воздействия тела на препятствие в момент удара, определено скоростью в момент соударения, а не средней скоростью движения тела. Форма траектории перемещения снаряда и его дальность полета зависит от скорости в момент запуска, а не от средней скорости.
Средняя скорость ($leftlangle vrightrangle $) движения материальной точки по оси X равна:
[leftlangle vrightrangle =frac{Delta x}{Delta t}left(1right),]
$Delta t$ — промежуток времени движения тела.
Определение
Мгновенную скорость определим как предел к которому стремится средняя скорость за бесконечно малый промежуток времени:
[v={mathop{lim }_{Delta tto 0} leftlangle vrightrangle }={mathop{lim }_{Delta tto 0} frac{Delta x}{Delta t}left(2right). }]
Такой предел в математике называют производной:
[v=frac{dx}{dt}=dot{x}left(3right).]
Выражение (3) обозначает, что мгновенная скорость (скорость в определенный момент времени) — производная от координаты. При прямолинейном движении материальной точки Мгновенную скорость можно определить как производную от пути ($s$) по времени:
[v=frac{ds}{dt}=dot{s}left(4right).]
Мгновенная скорость равномерного движения материальной точки
Средняя скорость равномерно движущейся точки величина постоянная, значит, мгновенная скорость равномерно перемещающейся точки является неизменной величиной.
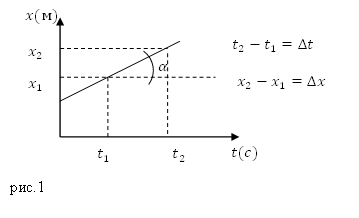
Скорость равномерного движения численно равна тангенсу угла наклона прямой к оси времени (рис.1):
[v=k tg alpha left(4right),]
где $k$ — безразмерный коэффициент, определяющий отношение масштаба единиц перемещения (ось ординат) и единиц времени (ось абсцисс).
При графическом изображении переменного движения материальной точки мгновенная скорость численно равна тангенсу угла наклона касательной к графику и осью абсцисс.
Мгновенная скорость при криволинейном движении
Положение материальной точки на траектории зададим радиус-вектором $overline{r}(t)$, который проведем в точку наблюдения из какой-либо неподвижной точки, которую примем за начало координат. Тогда мгновенной скоростью материальной точки будет векторная величина, равная:
[overline{v}=frac{doverline{r}}{dt}=dot{overline{r}}left(5right).]
скорость — это вектор, направленный по касательной к траектории движения материальной точки в месте нахождения частицы.
Примеры задач с решением
Пример 1
Задание. Две материальные точки движутся согласно уравнениям:
[left{ begin{array}{c}
x_1=-3t+4t^2-t^3(м) \
x_2=t-2t^2-t^3(м) end{array}
right.left(1.1right),]
в какой момент времени скорости этих точек будут равны?
Решение. В задаче речь идет о нахождении времени, когда будут равны мгновенные скорости материальных точек. Величину мгновенной скорости будем находить как:
[v=frac{dx}{dt}left(1.2right).]
Тогда подставляя по очереди уравнения из системы (1.1) получим:
[left{ begin{array}{c}
v_1=frac{dx_1}{dt}=-3+8t-3t^2 \
v_2=frac{dx_2}{dt}=1-4t-3t^2 end{array}
right.left(1.3right).]
Приравняем правые части уравнений в системе (1.3), найдем момент времени в который скорости равны ($v_1=v_2$):
[-3+8t-3t^2=1-4t-3t^2to 8t+4t=1+3to 12t=4to t=frac{1}{3}left(cright).]
Ответ. $t=frac{1}{3}$ с
Пример 2
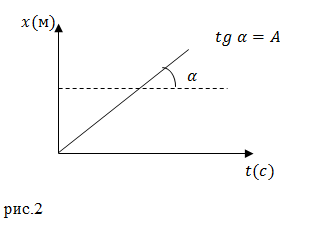
Задание. Материальная точка движется на плоскости XOY. Закон изменения координаты $x$ задан графиком рис.2 . Координата $y $задана аналитическим выражением: $y=At(1+Bt)$, где $A$ и $B$ постоянные величины. Запишите выражение, связывающее мгновенную скорость и время ($v(t)$).
Решение. Из рис. 2 мы можем записать уравнение, которое определяет изменение координаты $x$ от времени:
[xleft(tright)=At left(2.1right).]
Получили, что движение материальной точки в плоскости XOY описывают при помощи системы уравнений:
[left{ begin{array}{c}
xleft(tright)=At;; \
y=Atleft(1+Btright) end{array}
left(2.2right).right.]
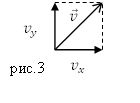
Найдем составляющие скорости движения материальной точки:
[v_x=frac{dx}{dt}=frac{d}{dt}left(Atright)=A;;]
[v_y=frac{dy}{dt}=frac{d}{dt}left(Atleft(1+Btright)right)=A+2ABt.]
Модуль скорости найдем как:
[v=sqrt{v^2_x+v^2_y}=sqrt{A^2+{(A+2ABt)}^2}=sqrt{A^2+A^2+2A^2Bt+4A^2B^2t^2}=]
[=Asqrt{2+2Bt+4B^2t^2.}]
Ответ. $v=Asqrt{2+2Bt+4B^2t^2}$
Читать дальше: механические волны.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Онлайн калькулятор равноускоренного движения помогает решить задачи на движение с равномерным ускорением (раздел кинематики).
При решении задач используется 5 параметров: начальная скорость (Vн), конечная скорость (Vк), ускорение (a),основное время движения (t) и перемещение (S). Чтобы найти все величины, нужно задать 3 параметра из 5.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Все формулы для равноускоренного движения с примерами в статье «Равноускоренное движение: определение и формулы«.