17 авг. 2022 г.
читать 2 мин
В этом руководстве объясняется, как рассчитать межквартильный диапазон набора данных в Excel.
Что такое межквартильный диапазон?
Межквартильный диапазон , часто обозначаемый IQR, — это способ измерения разброса средних 50% набора данных. Он рассчитывается как разница между первым квартилем* (Q1) и третьим квартилем (Q3) набора данных.
*Квартили — это просто значения, которые делят набор данных на четыре равные части.
Например, предположим, что у нас есть следующий набор данных:
[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]
Третий квартиль оказывается равным 91 , а первый квартиль равен 75,5.Таким образом, межквартильный размах (IQR) для этого набора данных составляет 91 – 75,5 = 15.Это говорит нам о том, насколько распределены средние 50% значений в этом наборе данных.
Как рассчитать межквартильный диапазон в Excel
В Microsoft Excel нет встроенной функции для расчета IQR набора данных, но мы можем легко найти ее с помощью функции КВАРТИЛЬ() , которая принимает следующие аргументы:
КВАРТИЛЬ(массив, кварта)
- массив: массив данных, которые вас интересуют.
- квартиль : квартиль, который вы хотите рассчитать.
Пример: поиск IQR в Excel
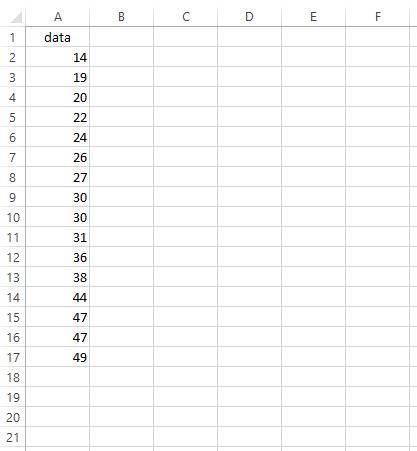
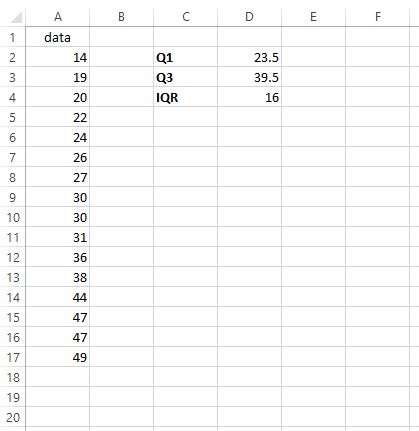
Предположим, мы хотим найти IQR для следующего набора данных:
Чтобы найти IQR, мы можем выполнить следующие шаги:
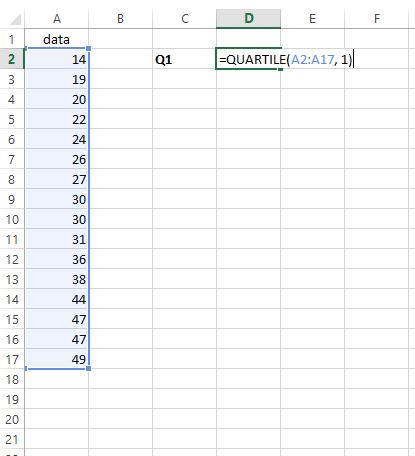
Шаг 1: Найдите Q1 .
Чтобы найти первый квартиль, мы просто вводим =КВАРТИЛЬ(A2:A17, 1) в любую выбранную ячейку:
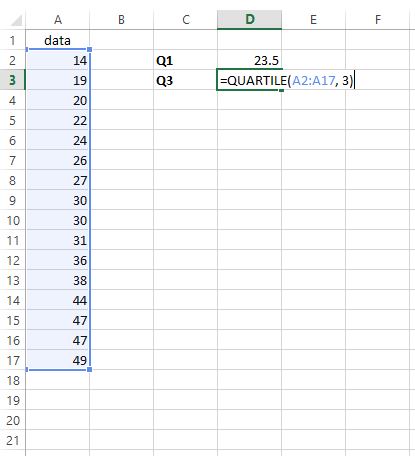
Шаг 2: Найдите Q3 .
Чтобы найти третий квартиль, мы вводим =КВАРТИЛЬ(A2:A17, 3) в любую выбранную ячейку:
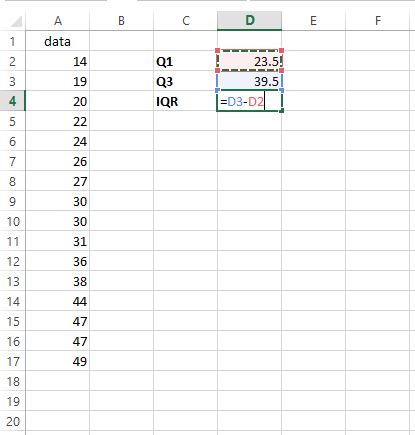
Шаг 3: Найдите IQR .
Чтобы найти межквартильный размах (IQR), мы просто вычитаем Q1 из Q3:
IQR оказывается равным 39,5 – 23,5 = 16.Это говорит нам о том, насколько распределены средние 50% значений в этом конкретном наборе данных.
Более короткий подход
Обратите внимание, что мы могли бы также найти межквартильный диапазон набора данных в предыдущем примере, используя одну формулу:
=КВАРТИЛЬ(A2:A17, 3) – КВАРТИЛЬ(A2:A17, 1)
Это также приведет к значению 16 .
Вывод
Межквартильный диапазон представляет собой только один из способов измерения «разброса» набора данных. Другими способами измерения разброса являются диапазон, стандартное отклонение и дисперсия .
Преимущество использования IQR для измерения спреда заключается в том, что он устойчив к выбросам.Поскольку он сообщает нам только разброс средних 50% набора данных, на него не влияют необычно маленькие или необычно большие выбросы.
Это делает его более предпочтительным способом измерения дисперсии по сравнению с таким показателем, как диапазон, который просто сообщает нам разницу между наибольшим и наименьшим значениями в наборе данных.
Связанный: Как рассчитать средний диапазон в Excel
В Excel функция КВАРТИЛЬ используется для разделения данных на равные доли. Также еще часто используют эту функцию для поиска отстающих показателей, то есть существенно отличающихся от остальных значений в исходных данных.
Пример расчета межквартильного диапазона для статистического анализа в Excel
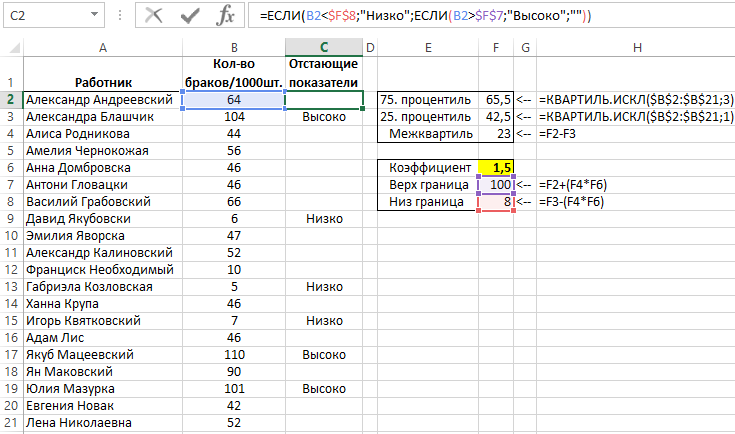
Ниже на рисунке представлен другой список работников с показателями производственных браков на 1000 шт. выпущенной продукции. Допустим нам необходимо узнать, какие работники делают большое и малое количество браков, существенно выходящее за пределы допустимой нормы (отстающие и превышающие ее — так называемые выборсы от медианы), чтобы потом проанализировать их. С целью поиска аномальных отклонений от показателей нормы в данном примере будет использован метод расширенного межквартильного диапазона. Межквартильный диапазон – это просто данные лежащие в среднем диапазоне, который охватывает 50% всего объема данных (находящийся между 75% и 25%). Определение «расширенный» значит, что средний диапазон данных может быть расширен с учетом определенного коэффициента, определяющего его границы. Все значения, лежащие вне границ, воспринимаются как показатели выборсы:
Для определения значения в среднем диапазоне между 75% и 25% следует воспользоваться функцией КВАРТИЛЬ.ИСКЛ вместе с указанными аргументами 3 и 1 – соответственно. Межквартильным диапазоном является разницей между этими значениями.
В случае нерасширенного межквартильного диапазона с целью определения его нижней границы достаточно всего лишь вычитать значение диапазона от 25%. А для верхней границы, нужно добавить его до 75%. Результатом применения данного метода могло бы получиться слишком большое число для найденных показателей выбросов. Умножая межквартильный диапазон на расширяющий коэффициент (в данном примере равен 1,5) расширяются границы. Таким образом, можно выбрать только особенно экстремальные значения.
Схема вычисления межквартильного диапазона в Excel
Ниже на рисунке представленные те же данные, что и в предыдущем примере, отсортированы по столбцу с показателями количества браков на 1000 шт. готовой продукции. Также для наглядности линиями наложены границы расширенного диапазона четверти и верхние с нижними границами остальных диапазонов четверти:
Чтобы определить верхнюю границу диапазона четверти, необходимо умножить расширяющий коэффициент на диапазон четверти и добавить его результат к 75%.
Чтобы определить нижнюю границу необходимо от 25% вычитать результат, полученный после умножения диапазона на коэффициент.
Может оказаться так, что расширяющий коэффициент равен 1,5 привел к исключению значения, которое казались отстающими или были выбраны значения, которые казались нормальными. В этом нет ничего особенного. Просто увеличьте или уменьшите расширяющий коэффициент, если его текущее значение не согласуются с Вашими исходными данными.
После определения границ используйте формулу со вложенными функциями ЕСЛИ с целью проверки: является ли данное значение большим чем верхнее или ниже от нижнего граничного значения. В случае значительных отклонений показателей (выбросов) от нормы формула со вложенными функциями ЕСЛИ возвращает слово «Выше» или «Ниже», а в случае значения лежащего внутри границ формула возвращает пустую строку («»).
Для вычисления квартилей в MS EXCEL существует специальная функция
КВАРТИЛЬ()
. В этой статье дадим определение квартилей и научимся их вычислять для выборки и для непрерывного распределения. Также вычислим интерквартильный интервал.
Квартили
(Quartiles) — значения, которые делят
выборку
(набор значений) на четыре части, содержащие приблизительно равное количество наблюдений (по 25%).
Поясним определение
квартиля
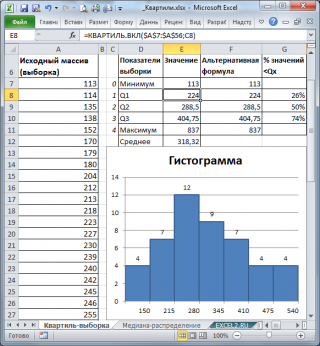
на примере. Пусть имеется
выборка
, состоящая из 50 значений в ячейках
А7:А56
(см.
файл примера
, лист Квартиль-выборка). Для наглядности
отсортируем значения по возрастанию
и построим
гистограмму
.
Чтобы разделить
выборку
на 4 части достаточно 3-х
квартилей
.
Первый
квартиль
(или
нижний квартиль
, Q1) делит
выборку
, на 2 части: примерно 25% значений в
выборке
меньше Q1, остальные 75% — больше. Для вычисления
1-го квартиля
используйте формулу
=КВАРТИЛЬ.ВКЛ(A7:A56;1)
. Для нашей выборки формула вернет значение 224. Значения 224 нет в
выборке
, формула произвела интерполяцию на основе 2-х соседних значений 223 и 227.
Примечание
: Функция
КВАРТИЛЬ.ВКЛ()
появилась в MS EXCEL 2010. В более ранних версиях использовалась аналогичная ей функция
КВАРТИЛЬ()
.
Чтобы убедиться, что примерно 25% значений меньше, чем 224, используем формулу
=СЧЁТЕСЛИ(A7:A56;»<«&224)/СЧЁТ(A7:A56)
. В результате получим, что 26% меньше, чем 1-й
квартиль
.
Чем в
выборке
больше значений и меньше
повторов
, тем точнее деление
выборки квартилями
на четверти.
Примечание
: Первый квартиль — это то же самое, что и 25-я
процентиль
. Подробнее см.
статью про процентили
.
Второй
квартиль
(или
медиана
, Q2) также делит
выборку
, на 2 равные части: половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для вычисления 2-го
квартиля
используйте формулу
=КВАРТИЛЬ.ВКЛ(A7:A56;2)
или
=МЕДИАНА(A7:A56)
Третий
квартиль
(или верхний
квартиль
, Q3) делит
выборку
, на 2 части: примерно 75% значений в
выборке
меньше Q3, остальные 25% — больше. Для вычисления 3-го
квартиля
используйте формулу
=КВАРТИЛЬ.ВКЛ(A7:A56;3)
или
=ПРОЦЕНТИЛЬ.ВКЛ(A7:A56;0,75)
Примечание
: Третий
квартиль
— это то же самое, что и 75-я
процентиль
.
Второй аргумент функции
КВАРТИЛЬ.ВКЛ()
может также принимать значения 0 и 4. В первом случае функция вернет
минимальное значение
, во втором –
максимальное
.
Интерквартильный размах
Интерквартильным размахом
или
интерквартильным интервалом
(InterQuartile range, IQR) называется разность между третьим и первым
квартилями
(Q3 — Q1).
Интерквартильный размах
является характеристикой разброса значений в
выборке
.
Примечание
: Характеристикой разброса значений в
выборке
является также
дисперсия и стандартное отклонение
.
Интерквартильный размах
, а также
квартили
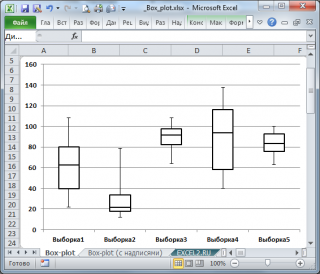
используются при построении
Блочной диаграммы
, которая полезна для оценки разброса значений (variation) в небольших
выборках
или для сравнения нескольких
выборок
имеющих сходные распределения.
Подробнее о построении
Блочной диаграммы
см. статью
Блочная диаграмма в MS EXCEL
.
Квартили непрерывного распределения
Если
функция распределения
F
(х)
случайной величины
х
непрерывна, то 1-й
квартиль
является решением уравнения
F(х)
=0,25, второй —
F(х)
=0,5, а третий
F(х)
=0,75.
Примечание
: Подробнее о
Функции распределения
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Если известна
функция плотности вероятности
p
(х)
, то 1-й
квартиль
можно найти из уравнения:
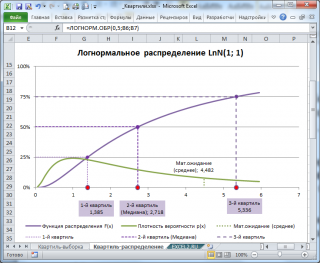
Например, решив аналитическим способом это уравнение для
Логнормального распределения
lnN(μ; σ
2
), получим, что
медиана
(2-й
квартиль
) вычисляется по формуле e
μ
или в MS EXCEL =EXP(μ). При μ=1,
медиана
равна 2,718.
Обратите внимание на точку
Функции распределения
, для которой
F(х)=0,5
(см. картинку выше или
файл примера
, лист Квартиль-распределение)
.
Абсцисса этой точки равна 2,718. Это и есть значение 2-го
квартиля
(
медианы
), что естественно совпадает с ранее вычисленным значением по формуле e
μ
.
Примечание
: Напомним, что интеграл от
функции плотности вероятности
по всей области задания случайной величины равен единице:
Поэтому, линии
квартилей
(
х=квартиль
) делят площадь под графиком
функции плотности вероятности
на 4 равные части.
Квартили в MS EXCEL
Чтобы вычислить в MS EXCEL
квартили
заданного распределения необходимо использовать соответствующую
обратную функцию распределения
.
При вычислении
квартилей
в MS EXCEL используются
обратные функции распределения
:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР()
,
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Например, в MS EXCEL 1-й
квартиль
для
логнормального распределения
LnN(1;1) можно вычислить по формуле
=ЛОГНОРМ.ОБР(0,25;1;1)
, а 3-й
квартиль
для
стандартного нормального распределения
по формуле
=НОРМ.СТ.ОБР(0,75)
.
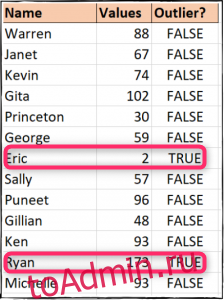
Быстрый пример
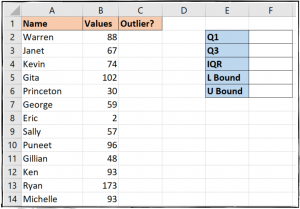
На изображении ниже выбросы довольно легко обнаружить — значение два присвоено Эрику, а значение 173 — Райану. В таком наборе данных достаточно легко обнаружить и обработать эти выбросы вручную.
В большем наборе данных этого не будет. Возможность идентифицировать выбросы и удалять их из статистических расчетов важна — и это то, что мы рассмотрим, как это сделать в этой статье.
Как найти выбросы в ваших данных
Чтобы найти выбросы в наборе данных, мы используем следующие шаги:
Вычислите 1-й и 3-й квартили (мы немного поговорим о том, что это такое).
Оцените межквартильный размах (мы также объясним это немного ниже).
Верните верхнюю и нижнюю границы нашего диапазона данных.
Используйте эти границы для определения отдаленных точек данных.
Диапазон ячеек справа от набора данных, показанного на изображении ниже, будет использоваться для хранения этих значений.
Давайте начнем.
Шаг 1. Рассчитайте квартили
Если вы разделите данные на кварталы, каждый из этих наборов называется квартилем. Самые низкие 25% чисел в диапазоне составляют 1-й квартиль, следующие 25% — 2-й квартиль и т. Д. Мы делаем этот шаг в первую очередь, потому что наиболее широко используемое определение выброса — это точка данных, которая более чем на 1,5 интерквартильных диапазонов (IQR) ниже 1-го квартиля и на 1,5 межквартильных диапазонов выше 3-го квартиля. Чтобы определить эти значения, мы сначала должны выяснить, каковы квартили.
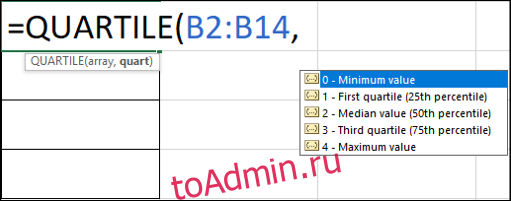
Excel предоставляет функцию КВАРТИЛЬ для расчета квартилей. Для этого требуются две части информации: массив и кварта.
=QUARTILE(array, quart)
Массив — это диапазон значений, которые вы оцениваете. Кварта — это число, которое представляет квартиль, который вы хотите вернуть (например, 1 для 1-го квартиля, 2 для 2-го квартиля и т. Д.).
Примечание. В Excel 2010 Microsoft выпустила функции QUARTILE.INC и QUARTILE.EXC как усовершенствования функции QUARTILE. QUARTILE более обратно совместима при работе с несколькими версиями Excel.
Вернемся к нашему примеру таблицы.
Для вычисления 1-го квартиля мы можем использовать следующую формулу в ячейке F2.
=QUARTILE(B2:B14,1)
Когда вы вводите формулу, Excel предоставляет список параметров для аргумента кварты.
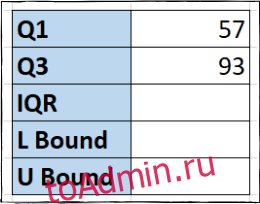
Чтобы вычислить 3-й квартиль, мы можем ввести формулу, аналогичную предыдущей, в ячейку F3, но используя тройку вместо единицы.
=QUARTILE(B2:B14,3)
Теперь у нас есть точки данных квартилей, отображаемые в ячейках.
Шаг второй: оцените межквартильный размах
Межквартильный диапазон (или IQR) — это средние 50% значений в ваших данных. Он рассчитывается как разница между значением 1-го квартиля и значением 3-го квартиля.
Мы собираемся использовать простую формулу в ячейке F4, которая вычитает 1-й квартиль из 3-го квартиля:
=F3-F2
Теперь мы можем видеть наш межквартильный размах.
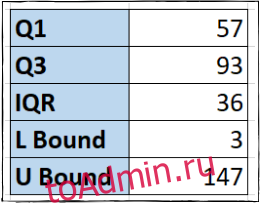
Шаг третий: верните нижнюю и верхнюю границы
Нижняя и верхняя границы — это наименьшее и наибольшее значение диапазона данных, который мы хотим использовать. Любые значения, меньшие или большие, чем эти связанные значения, являются выбросами.
Мы рассчитаем нижний предел в ячейке F5, умножив значение IQR на 1,5, а затем вычтя его из точки данных Q1:
=F2-(1.5*F4)
Примечание. Скобки в этой формуле не нужны, потому что часть умножения будет вычисляться перед частью вычитания, но они облегчают чтение формулы.
Чтобы вычислить верхнюю границу в ячейке F6, мы снова умножим IQR на 1,5, но на этот раз добавим его к точке данных Q3:
=F3+(1.5*F4)
Шаг четвертый: выявление выбросов
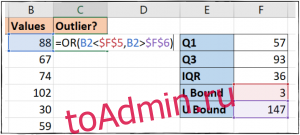
Теперь, когда мы настроили все наши базовые данные, пришло время определить наши отдаленные точки данных — те, которые ниже значения нижней границы или выше значения верхней границы.
Мы будем использовать Функция ИЛИ для выполнения этого логического теста и отображения значений, соответствующих этим критериям, введите следующую формулу в ячейку C2:
=OR(B2$F$6)
Затем мы скопируем это значение в наши ячейки C3-C14. Значение ИСТИНА указывает на выброс, и, как видите, в наших данных их два.
Игнорирование выбросов при вычислении среднего среднего
Использование функции КВАРТИЛЬ позволяет нам рассчитать IQR и работать с наиболее широко используемым определением выброса. Однако при вычислении среднего среднего для диапазона значений и игнорировании выбросов существует более быстрая и простая функция. Этот метод не будет определять выбросы, как раньше, но он позволит нам быть гибкими в выборе того, что мы можем считать своей частью выбросов.
Нужная нам функция называется TRIMMEAN, синтаксис для нее вы можете увидеть ниже:
=TRIMMEAN(array, percent)
Массив — это диапазон значений, которые вы хотите усреднить. Процент — это процент точек данных, которые необходимо исключить из верхней и нижней части набора данных (вы можете ввести его как процентное или десятичное значение).
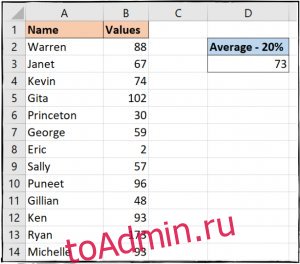
В нашем примере мы ввели приведенную ниже формулу в ячейку D3, чтобы вычислить среднее значение и исключить 20% выбросов.
=TRIMMEAN(B2:B14, 20%)
Здесь у вас есть две разные функции для обработки выбросов. Независимо от того, хотите ли вы идентифицировать их для каких-либо потребностей в отчетности или исключить их из вычислений, таких как средние значения, в Excel есть функция, соответствующая вашим потребностям.
Содержание:
- Что такое выбросы и почему их важно найти?
- Найдите выбросы путем сортировки данных
- Поиск выбросов с помощью квартильных функций
- Поиск выбросов с помощью функций НАИБОЛЬШИЙ / МАЛЕНЬКИЙ
- Как правильно обращаться с выбросами
- Удалить выбросы
- Нормализовать выбросы (отрегулировать значение)
При работе с данными в Excel у вас часто возникают проблемы с обработкой выбросов в наборе данных.
Выбросы довольно часто встречаются во всех видах данных, и важно идентифицировать и обрабатывать эти выбросы, чтобы убедиться, что ваш анализ правильный и значимый.
В этом уроке я покажу вам как найти выбросы в Excel, а также некоторые методы, которые я использовал в своей работе для обработки этих выбросов.
Что такое выбросы и почему их важно найти?
Выброс — это точка данных, которая выходит за рамки других точек данных в наборе данных. Если у вас есть выброс в данных, это может исказить ваши данные, что может привести к неверным выводам.
Приведу простой пример.
Допустим, 30 человек едут на автобусе из пункта назначения A в пункт назначения B. Все люди относятся к одной весовой группе и группе доходов. Для целей этого руководства давайте предположим, что средний вес составляет 220 фунтов, а средний годовой доход — 70 000 долларов.
Сейчас где-то посередине нашего маршрута автобус останавливается, и в него садится Билл Гейтс.
Как вы думаете, как это повлияет на средний вес и средний доход людей в автобусе?
Хотя средний вес вряд ли сильно изменится, средний доход пассажиров автобуса резко вырастет.
Это связано с тем, что доход Билла Гейтса является исключением в нашей группе, и это дает нам неправильную интерпретацию данных. Средний доход каждого пассажира автобуса составит несколько миллиардов долларов, что намного превышает реальную стоимость.
При работе с фактическими наборами данных в Excel вы можете иметь выбросы в любом направлении (например, положительный выброс или отрицательный выброс).
И чтобы убедиться, что ваш анализ верен, вам нужно каким-то образом идентифицировать эти выбросы, а затем решить, как лучше всего их лечить.
Теперь давайте рассмотрим несколько способов найти выбросы в Excel.
Найдите выбросы путем сортировки данных
С небольшими наборами данных быстрый способ определить выбросы — просто отсортировать данные и вручную просмотреть некоторые значения в верхней части отсортированных данных.
А так как выбросы могут быть в обоих направлениях, убедитесь, что вы сначала отсортировали данные в порядке возрастания, а затем в порядке убывания, а затем перебрали самые верхние значения.
Позвольте мне показать вам пример.
Ниже у меня есть набор данных, в котором у меня есть продолжительность звонков (в секундах) для 15 звонков в службу поддержки.
Ниже приведены шаги по сортировке этих данных, чтобы мы могли идентифицировать выбросы в наборе данных:
- Выберите заголовок столбца, который вы хотите отсортировать (в этом примере ячейка B1).
- Перейдите на вкладку «Главная«
- В группе «Редактирование» щелкните значок «Сортировка и фильтр».
- Щелкните Custom Sort (Пользовательская сортировка).
- В диалоговом окне «Сортировка» выберите «Продолжительность» в раскрывающемся списке «Сортировка по» и «От наибольшего к наименьшему» в раскрывающемся списке «Порядок».
- Нажмите ОК
Вышеупомянутые шаги сортируют столбец продолжительности звонка с наивысшими значениями вверху. Теперь вы можете вручную просмотреть данные и посмотреть, есть ли выбросы.
В нашем примере я вижу, что первые два значения намного выше остальных значений (а два нижних намного ниже).
Примечание. Этот метод работает с небольшими наборами данных, где вы можете вручную сканировать данные. Это не научный метод, но он хорошо работает
Поиск выбросов с помощью квартильных функций
Теперь давайте поговорим о более научном решении, которое поможет вам определить, есть ли какие-то выбросы.
В статистике квартиль составляет четверть набора данных. Например, если у вас есть 12 точек данных, то первый квартиль будет тремя нижними точками данных, второй квартиль будет следующими тремя точками данных и так далее.
Ниже приведен набор данных, по которому я хочу найти выбросы. Для этого мне нужно будет вычислить 1-й и 3-й квартили, а затем с его помощью вычислить верхний и нижний предел.
Ниже приведена формула для вычисления первого квартиля в ячейке E2:
= QUARTILE.INC ($ B $ 2: $ B $ 15,1)
и вот тот, который вычисляет третий квартиль в ячейке E3:
= QUARTILE.INC ($ B $ 2: $ B $ 15,3)
Теперь я могу использовать два вышеупомянутых вычисления, чтобы получить межквартильный размах (который составляет 50% наших данных в пределах 1-го и 3-го квартилей).
= F3-F2
Теперь мы будем использовать межквартильный диапазон, чтобы найти нижний и верхний предел, который будет содержать большую часть наших данных.
Все, что выходит за эти нижние и верхние пределы, будет считаться выбросом.
Ниже приведена формула для расчета нижнего предела:
= Квартиль1 - 1,5 * (Межквартильный диапазон)
который в нашем примере становится:
= F2-1,5 * F4
И формула для расчета верхнего предела:
= Квартиль3 + 1,5 * (Межквартильный диапазон)
который в нашем примере становится:
= F3 + 1,5 * F4
Теперь, когда у нас есть верхний и нижний предел в нашем наборе данных, мы можем вернуться к исходным данным и быстро определить те значения, которые не лежат в этом диапазоне.
Быстрый способ сделать это — проверить каждое значение и вернуть ИСТИНА или ЛОЖЬ в новом столбце.
Я использовал приведенную ниже формулу ИЛИ, чтобы получить ИСТИНА для тех значений, которые являются выбросами.
= ИЛИ (B2 $ F $ 6)
Теперь вы можете фильтровать столбец Outlier и отображать только те записи, для которых значение TRUE.
Кроме того, вы также можете использовать условное форматирование, чтобы выделить все ячейки, в которых значение TRUE.
Примечание: Хотя это более распространенный метод поиска выбросов в статистике. Я считаю, что этот метод немного непригоден для использования в реальных сценариях. В приведенном выше примере нижний предел, рассчитанный по формуле, равен -103, в то время как набор данных, который у нас есть, может быть только положительным. Таким образом, этот метод может помочь нам найти выбросы в одном направлении (высокие значения), он бесполезен при выявлении выбросов в другом направлении.
Поиск выбросов с помощью функций НАИБОЛЬШИЙ / МАЛЕНЬКИЙ
Если вы работаете с большим количеством данных (значения в нескольких столбцах), вы можете извлечь 5 или 7 наибольших и наименьших значений и посмотреть, есть ли в них выбросы.
Если есть какие-либо выбросы, вы сможете их идентифицировать, не просматривая все данные в обоих направлениях.
Предположим, у нас есть приведенный ниже набор данных, и мы хотим знать, есть ли какие-либо выбросы.
Ниже приведена формула, которая даст вам наибольшее значение в наборе данных:
= БОЛЬШОЙ ($ B $ 2: $ B $ 16,1)
Точно так же второе по величине значение будет равно
= БОЛЬШОЙ ($ B $ 2: $ B $ 16,1)
Если вы не используете Microsoft 365, в которой есть динамические массивы, вы можете использовать приведенную ниже формулу, и она даст вам пять наибольших значений из набора данных с помощью одной формулы:
= БОЛЬШОЙ ($ B $ 2: $ B $ 16; СТРОКА ($ 1: 5))
Точно так же, если вам нужны 5 наименьших значений, используйте следующую формулу:
= МАЛЕНЬКИЙ ($ B $ 2: $ B $ 16; СТРОКА ($ 1: 5))
или следующее, если у вас нет динамических массивов:
= МАЛЕНЬКИЙ ($ B $ 2: $ B $ 16,1)
Когда у вас есть эти значения, очень легко обнаружить любые выбросы в наборе данных.
Хотя я решил извлечь 5 наибольших и наименьших значений, вы можете выбрать 7 или 10 в зависимости от размера вашего набора данных.
Я не уверен, является ли это приемлемым методом для поиска выбросов в Excel или нет, но это метод, который я использовал, когда мне приходилось работать с большим количеством финансовых данных на моей работе несколько лет назад. По сравнению со всеми другими методами, описанными в этом руководстве, я считаю этот наиболее эффективным.
Как правильно обращаться с выбросами
До сих пор мы видели методы, которые помогут нам найти выбросы в нашем наборе данных. Но что делать, если вы знаете, что есть выбросы.
Вот несколько методов, которые вы можете использовать для обработки выбросов, чтобы ваш анализ данных был правильным.
Удалить выбросы
Самый простой способ удалить выбросы из набора данных — просто удалить их. Таким образом, это не исказит ваш анализ.
Это более жизнеспособное решение, когда у вас большие наборы данных и удаление пары выбросов не повлияет на общий анализ. И, конечно же, перед удалением данных обязательно создайте копию и выясните, что вызывает эти выбросы.
Нормализовать выбросы (отрегулировать значение)
Нормализация выбросов — это то, что я делал, когда работал полный рабочий день. Для всех значений выбросов я бы просто изменил их на значение, немного превышающее максимальное значение в наборе данных.
Это гарантирует, что я не удаляю данные, но в то же время не позволяю им искажать мои данные.
Чтобы дать вам реальный пример, если вы анализируете маржу чистой прибыли компаний, где большинство компаний находится в пределах от -10% до 30%, а есть несколько значений, превышающих 100%, я просто изменит эти выбросы на 30% или 35%.
Итак, вот некоторые из методов, которые вы можете использовать в Excel, чтобы найти выбросы.
После того, как вы определили выбросы, вы можете углубиться в данные и посмотреть, что их вызывает, и в то же время выбрать один из методов обработки этих выбросов (который может удалить их или нормализовать, изменив значение)
Надеюсь, вы нашли этот урок полезным.