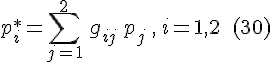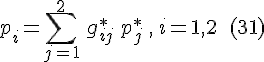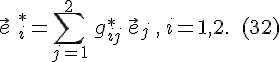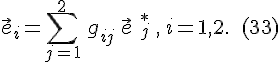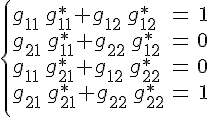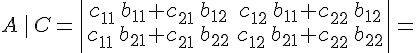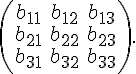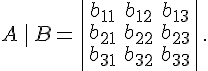Как найти метрические коэффициенты базиса

Выражение скалярного произведения через координаты векторов

Разумеется, что величина скалярного произведения любых векторов и не зависит от базиса. Однако формулы, выражающие скалярное произведение через координаты множителей, зависят от базиса, относительно которого определены координаты. Рассмотрим сначала случай стандартного базиса в пространстве, а затем — произвольного.

Скалярное произведение векторов в ортонормированном базисе

Теорема 1.6 (формула вычисления скалярного произведения в ортонормированном базисе). В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов:

— если векторы и относительно ортонормированного базиса на плоскости имеют координаты и соответственно, то скалярное произведение этих векторов вычисляется по формуле

— если векторы и относительно ортонормированного базиса в пространстве имеют координаты и соответственно, то скалярное произведение этих векторов вычисляется по формуле

Докажем формулу (1.10). Пусть в пространстве задан ортонормированный (стандартный) базис . Скалярные произведения базисных векторов находятся по определению:

Используя линейность скалярного произведения по любому множителю, для векторов и получаем:

Учитывая (1.11), из девяти слагаемых только три отличны от нуля, поэтому

что и требовалось доказать.

Замечания 1.10

1. Для доказательства формулы (1.9) можно использовать следующее соображение. Множество векторов на плоскости со стандартным базисом можно рассматривать как множество таких векторов в пространстве с базисом , у которых аппликата равна нулю. Поэтому формулу вычисления скалярного произведения векторов и можно получить из (1.10), полагая .

2. Скалярное произведение можно записать в матричном виде: если и координатные столбцы векторов и в стандартном базисе, то их скалярное произведение находится формуле:

Для векторов на плоскости соответственно получаем

3. Координаты вектора в ортонормированием базисе равны его скалярным произведениям на соответствующие базисные векторы:

В самом деле, подставляя в (1.10) координаты базисного вектора , приходим к первому равенству (остальные равенства получаются аналогично).

4. Формулы (1.9) и (1.10) совместно с геометрическими свойствами скалярного произведения имеют многочисленные приложения.

Пример 1.15. Даны векторы . Найти скалярные произведения

Решение. По формуле (1.10) вычисляем

Сравнивая вектор со скалярными произведениями обнаруживаем, что при умножении вектора на базисный вектор получается соответствующая координата данного вектора. Этот результат иллюстрирует пункт 3 замечаний 1.10.

Для нахождения скалярного произведения можно использовать матричную запись (см. пункт 2 замечаний 1.10). Например, векторам соответствуют координатные столбцы

Поэтому

что совпадает с полученными ранее результатами.

Пример 1.16. Прямоугольный параллелепипед построен на векторах (см. рис. 1.38). Точка — центр грани , точка делит ребро в отношении . Требуется найти:

а) величину угла между векторами и ;

б) длину ортогональной проекции вектора на прямую .

Решение. Находим координаты векторов в стандартном базисе :

(см. решение примера 1.12)

По формуле (1.10) находим скалярные произведения:

а также длины векторов (см. геометрическое свойство 1 скалярного произведения):

Длина была найдена в примере 1.12.

Теперь по геометрическому свойству 2 находим косинус искомого угла

т.е.

Алгебраическое значение длины ортогональной проекции находим по геометрическомусвойству 3:

Скалярное произведение векторов в произвольном базисе

Пусть — произвольный базис в пространстве. Найдем скалярное произведение векторов и :

Запишем полученную формулу в матричном виде. Для этого из чисел , называемых метрическими коэффициентами базиса, составим матрицу Грама системы векторов :

Координаты каждого из векторов и представим в виде столбцов

и соответственно.

Тогда для скалярного произведения получим

или, короче,

Теорема 1.7 (формула вычисления скалярного произведения в произвольном базисе). В произвольном базисе скалярное произведение векторов и вычисляется по формуле (1.13), где — координатные столбцы векторов и соответственно, a —матрица Грама (1.12) базиса .

Замечания 1.11.

1. Для ортонормированного базиса матрица Грама имеет вид

т.е. является единичной. В этом случае по формуле (1.13) получаем

что совпадает с (1.10).

2. Для произвольного базиса на плоскости скалярное произведение векторов и находится по формуле:

где — координатные столбцы векторов и соответственно, a — матрица Грама базиса .

В частности, для ортонормированного базиса матрица Грама является единичной: , поэтому скалярное произведение векторов и находится по формуле , что совпадает с (1.9). Заметим, что эта формула также следует из полученной в пункте 1 при .

Пример 1.17. Найти матрицы Грама для следующих базисов:

а) два единичных вектора , служащие сторонами правильного треугольника (рис.1.39,а);

б) три единичных вектора , служащие ребрами правильного тетраэдра (рис. 1.39,6).

Найти длины векторов, имеющих в данных базисах следующие разложения: .

Решение. а) Учитывая, что длины базисных векторов равны единице, а угол между ними равен , получаем

Записываем матрицу Грама

Найдем теперь длину вектора . Составляем координатный столбец этого вектора .

Учитывая формулу (1.13), находим скалярный квадрат: . Следовательно, .

б) Учитывая, что длины базисных векторов равны единице, а угол между любыми двумя из них равен , получаем

Записываем матрицу Грама: . Найдем теперь длину вектора . Составляем координатный столбец этого вектора . Учитывая формулу (1.13), находим скалярный квадрат:

Следовательно,

Скалярное произведение векторов во взаимных базисах

Пусть на плоскости задан базис . Базис называется взаимным по отношению к базису , если

Пусть в пространстве задан базис . Базис называется взаимным по отношению к базису , если

Взаимные базисы обладают следующими основными свойствами.

1. Свойство взаимности базисов симметричное: если второй базис взаимен по отношению к первому, то первый взаимен ко второму.

2. Для каждого базиса (на плоскости или в пространстве) существует единственный взаимный базис.

3. Пусть векторы и заданы своими координатами относительно взаимных базисов:

Тогда их скалярное произведение вычисляется по формуле: , т.е. равно сумме произведений одноименных координат векторов, как и в случае ортонормированного базиса.

4. Если и взаимные базисы, то координаты любого вектора относительно базиса находятся по формулам

Докажем свойство 2. Пусть на плоскости задан базис (рис.1.40,а). Вектор взаимного базиса перпендикулярен вектору , так как (см. второе геометрическое свойство скалярного произведения). Из двух возможных направлений для вектора выбираем то, которое образует острый угол с вектором , так как . Следовательно, направление вектора определено однозначно. Осталось выбрать его длину, используя (1.7): , так как .

Таким образом, направление и длина первого вектора взаимного базиса определяются однозначно. То же можно сказать и в отношении выбора вектора . Доказательство существования и единственности взаимного базиса в пространстве (рис. 1.40,6) проводится аналогично.

Заметим, что для стандартного базиса на плоскости (или базиса в пространстве) взаимный базис совпадает с самим базисом (соответственно )

Докажем свойство 3. Находим скалярное произведение, используя свойства коммутативности и линейности, а также определение взаимных базисов:

что и требовалось доказать.

Свойство 4 следует из формулы, приведенной в пункте З. В самом деле, . Аналогично доказываются остальные формулы в п.4.

Пример 1.18. а) Найти базис, взаимный базису, заданному в примере 1.17,а (рис.1.39,а).

б) Внутри угла величиной взята точка , удаленная от сторон и на расстояния 11 и 2 соответственно. Найти длину отрезка (рис.1.41,б).

Решение. а) Так как базисный вектор единичный, то, учитывая геометрический смысл скалярного произведения (см. разд. 1.4.1), вектор можно построить следующим образом. Через начало вектора (точку ) и конец вектора (точку ) проводим прямые, перпендикулярные векторам и соответственно (штриховые линии на рис. 1.41,а). Точка пересечения этих прямых — конец вектора (его начало совпадает с точкой ). Аналогично строится вектор (построение изображено штрих- пунктирными линиями на рис. 1.41,а). Тогда по построению справедливо , а также . Следовательно, учитывая геометрическое свойство 2 и формулу (1.8): , т.е. выполняются условия взаимности базисов. Найдем длины векторов взаимного базиса. Поскольку угол между векторами и равен (напомним, что ), то из прямоугольного треугольника с катетом . Длина вектора такая же.

б) Зададим на плоскости базис из единичных векторов , который совпадает с базисом, рассмотренным в пункте «а». По условию задачи известны длины ортогональных проекций вектора на оси, определяемые векторами взаимного базиса: . По третьему геометрическому свойству скалярного произведения с учетом свойства 4 взаимных базисов, получаем

где — координаты вектора в базисе . Так как (см. пункт «а»), то . Длину вектора вычисляем по формуле, следующей из пункта 2 замечаний 1.10 при , используя матрицу Грама для базиса , найденную в примере 1.17 пункт «а»:

Следовательно, .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Пусть
на плоскости введен произвольный
аффинный базис .
Введем следующие обозначения для
скалярных квадратов базисных векторов
и самого скалярного произведения данных
векторов:

Из
свойств скалярного произведения следует,
что .
Совокупность чисел  будем
называть метрическими коэффициентами
базиса .

Наряду
с базисом  рассмотрим
еще базис .

Определение
20.1. Базисы  и  называются
взаимными, если

В
случае двумерного векторного
подпространства (множества векторов
параллельных некоторой плоскости)
взаимные базисы допускают простую
геометрическую интерпретацию. Другими
словами, можно указать способ построения
взаимного базиса к заданному. Действительно,
пусть  —
данный базис. Тогда вектор  перпендикулярен
вектору  и
образует острый угол с вектором  ,
и, аналогично,  перпендикулярен
вектору  и
образует острый угол с вектором .
Длины векторов  определятся
условием .

Точно
так же определим метрические
коэффициенты  базиса .

Рассмотрим
произвольный вектор  плоскости
и разложим его по векторам  и .
Получим

Определение
20.2. Коэффициенты  называются
контравариантными координатами , а  —
ковариантными координатами вектора  в
базисе .

Рассмотрим
теперь два вектора  и  ,
разложим их по векторам ,
а также по векторам :

Используя
данные представления векторов  и ,
вычислим их скалярное произведение
четырьмя способами:

Мы
видим, что удобнее всего находить
скалярное произведение двух векторов,
если один вектор задан ковариантными,
а другой контравариантными координатами.
Установим связь контравариантных
координат  с
ковариантными координатами  одного
и того же вектора .
Из соотношения  находим

или

или
короче

Аналогично
находим

Установим
связь между взаимными базисами. Для
этого разложим базисные векторы  по
векторам :

Умножая
скалярно обе части первого из этих
соотношений на  и ,
получим

и
аналогично из второго соотношения

Мы
приходим к формулам:

Подобным
образом выводится соотношение

Найдем
теперь формулы для вычисления метрических
коэффициентов взаимного базиса, по
известным метрическим коэффициентам
исходного базиса. Для этого распишем
формулы  подробно.
Получаем:

Умножая
скалярно обе части каждого из этих
соотношений на  и ,
получим

Используя
ранее введенные обозначения и определение
взаимных базисов, приходим к следующей
системе линейных уравнений относительно
неизвестных 

Решая
эту систему приходим к следующим
выражениям для метрических коэффициентов
взаимного базиса с учетом, что  и 

где  .

21 Ориентация плоскости и пространства.

Для
простоты вычислений рассмотрим подробно
как определяется ориентация плоскости.
Пусть  —
множество всех векторов, параллельных
плоскости, т.е. двумерное подпространство
пространства .
Как известно, любые два неколлинеарных
вектора из ,
взятые в определенном порядке, образуют
базис .
Поэтому в  существует
бесконечное множество базисов. Рассмотрим
два из них:  и .
Разложим векторы базиса  по
векторам базиса :

Из
координат векторов  и  можно
составить матрицу второго порядка:

Координаты
вектора  образуют
первый столбец этой матрицы, а координаты
вектора  —
второй столбец. Эту матрицу назовем
матрицей перехода от базиса  к
базису .

Определение
21.1. Число  называется
определителем матрицы перехода от
базиса  к
базису  и
обозначается так:

Так
как векторы  и  линейно
независимы, то из следствия о координатах
коллинеарных векторов получаем, что .
Рассмотрим некоторые свойства
определителей матрицы перехода от
одного базиса к другому.

1. Для
любого базиса  имеем .

В
самом деле,  поэтому

2. Для
любых трех базисов  справедливо
равенство

Пусть .
Подставив в правые части этих формул
вместо  и  их
разложения по формулам ,
будем иметь:

Отсюда
получаем определитель матрицы перехода
от базиса  к
базису :

поскольку
определитель матрицы перехода от
базиса  к
базису  имеет
вид:

3. Для
любых базисов  справедливо
равенство

Действительно,
если в равенстве  положить  и
воспользоваться свойством 1., то получим
требуемое.

Обозначим
через  множество
всех базисов подпространства .
Будем говорить, что базисы  находятся
в отношении  (
одинаково ориентированы), если ,
записываем так .
Докажем, что отношение  является
отношением эквивалентности на
множестве  всех
базисов
подпространства .
Для этого необходимо проверить, что
отношение  удовлетворяет
свойствам рефлексивности, симметричности
и транзитивности.

1.рефлексивность. Для
произвольного базиса  по
свойству 1 имеем:

2.симметричность. Пусть .
Но из свойства 3 следует, что 

3. транзитивность. Непосредственно
следует из свойства 2.

Докажем,
что фактор-множество  состоит
лишь из двух элементов. Для этого
рассмотрим базисы  и
$bar A={vec a_2;vec a_1}$ . Так как  то
классы эквивалентности  и  различны.
Легко убедиться, что любой базис  принадлежит
либо классу ,
либо классу .
В самом деле, по свойству 2
.
Но ,
поэтому ,
отсюда либо ,
либо .

Каждый
из элементов фактор-множества  называется
ориентацией векторного подпространства .
Выделим одну из этих ориентаций, назовем
ее положительной ( а другую — отрицательной).
Векторное подпространство, в котором
выбрана положительная ориентация,
называется ориентированным. Базисы
положительной ориентации называют
правыми базисами, а базисы отрицательной
ориентации — левыми.

Аналогичным
образом определяется ориентация
векторного пространства .
А именно,как известно, любые три
некомпланарных вектора из ,
взятые в определенном порядке, образуют
базис .
Поэтому
в  существует
бесконечное множество базисов. Рассмотрим
два из них:  и .
Разложим векторы базиса  по
векторам базиса :

Из
координат векторов  и  можно
составить матрицу третьего порядка:

Координаты
вектора  образуют
первый столбец этой матрицы, координаты
вектора  —
второй столбец, а координаты вектора  —
третий столбец. Эту матрицу назовем
матрицей перехода от базиса  к
базису .
Определение
21.2. Число 

называется
определителем матрицы перехода от
базиса  к
базису  и
обозначается так:

Так
как векторы  и  линейно
независимы, то можно показать, что .

Точно
так же проверяются свойства определителей
матриц перехода и доказывается, что
существуют всего две различные ориентации
векторного пространства .
В дальнейшем будем считать, что векторное
пространство ориентировано и положительную
ориентацию определяет правая тройка
векторов.

Определение
21.3. Тройка
некомпланарных векторов, взятых в данном
порядке, называется правой (левой), если
кратчайший поворот от первого вектора
ко второму виден из конца третьего
совершающимся против (по) часовой
стрелке, при условии, что векторы
приведены к общему началу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  30.03.201527.55 Mб32Административное право России Конин Н.М..pdf

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Действительно, в декартовойпрямоугольной системе координат все три координаты х1 = х,х2 = у, х3 = z имеют размерность длины, поэтому метриче­ские коэффициенты (1.30) являются безразмерными величина­ми. В цилиндрической системе координат только две коорди­наты х1 = г и х3 = z имеют размерность длины, тогда какугловая координата х2 = в измеряется в радианах. Согласноэтому метрический коэффициент #22 =является размернойвеличиной с размерностью квадрата длины, в то время какдва других коэффициента являются безразмерными величи­нами (см. (1.31)).Взаимный базис системы координат.

Метриче­ские коэффициенты взаимного базиса. Взаимный (поотношению к основному) базис системы координат в даннойточке пространства есть совокупность трех векторов(или г1, г2, г3), которые взаимосвязаны с векторами основ­ного базиса соотношением(1.32)Согласно определению (1.32), скалярное произведение векто­ров основного (гг) и взаимного (г3) базисов обусловлено значе­нием символа Кронекера : скалярное произведение базисныхвекторов с одинаковыми индексами равно единице; результа­том перемножения базисных векторов с разными индексамиявляется нуль.

Определение (1.32) позволяет по известнымвекторам основного базиса построить совокупность трех век­торов взаимного базиса. Например, для первого из вектороввзаимного базисаг1 • 7*1 = 1,52г1 • Г2 = 0,Г1 • 7*3 = 0.(1.33)Как следует из этих соотношений, первый вектор взаимногобазиса г1 должен быть ортогонален обоим векторам основногобазиса 7*2 и г3- Следовательно, вектор т*1 = т(т*2 X ^з) Дол­жен быть коллинеарен векторному произведению Г2 X т*з, гдезначение скалярного множителя т определяется из первого со­отношения (1.33): 7*1 • m (т*2 X т*з) = 1.

Значение т обратно поотношению к смешанному произведению векторов основногобазиса 7*1 • (т*2 X т*з), которое равно объему параллелепипеда,построенного на векторах основного базиса. Для ортогональ­ных систем координат смешанное произведение определяетсяпроизведением модулей базисных векторов т*г. С учетом опре­деления метрических коэффициентов основного базиса (1.25)получим7*1 • (г2 X 7*3) = |т*1| • |Г2| • |^з| == х/(п Т1)-(Г2 • 7-2)-(т-з тз) =где д =— детерминант метрической матрицы(1.28) для ортогональной системы координат. Таким образом,скалярный множитель т = 1/у/д, что позволяет найти первыйвектор взаимного базиса: г1 = (7*2 х//д.

Аналогичноопределяются второй и третий векторы взаимного базиса г2И 7*3.Уточним геометрическоепредставление взаимного ба­зиса.В общем случае не­ортогональной криволинейнойсистемы координат (рис. 1.37)векторы основного базиса7*1, г2, г3 не являются ортого­нальными, а векторы взаим­ного базиса 7’1,т*2,7*3 не со­впадают с одноименнымиРис. 1.3753(имеющими одинаковые индексы, например, rj и г1) векто­рами основного базиса ни по направлению, ни по модулю.В случае ортогональной криволинейной системы координатвекторы основного базиса взаимно перпендикулярны, одно­именные векторы основного и взаимного базисов совпадаютпо направлению, но могут не совпадать по модулю (рис.

1.38).Наконец, в декартовойпрямоугольной системе ко­ординат векторы взаимно­го базиса, построенные всоответствии с определе­нием (1.32), совпадают помодулю и направлению сединичнымивекторамиосновного базиса: г1 =•о— Г1 —г ~ г2 = Зчг3 = гз = к.Метрические коэффициенты взаимного базиса системыкоординат вводятся с использованием векторов взаимного ба­зиса как величины, определяемые скалярным произведениемсоответствующих базисных векторов, т.е.gij = ri.rj(! .34)Совокупность девяти метрических коэффициентов д1] образу­ет метрическую матрицу взаимного базиса (И) , котораятак же, как и метрическая матрица основного базиса, являетсясимметричной:У<712U1399229239“923<733 J>Для ортогональной системы координат метрическая матрицаявляется диагональной:54Между метрическими коэффициентами основного и вза­имного базисов существует взаимосвязь, которую приведембез вывода: дгг =Таким образом, в декартовой пря­моугольной системе координат (<7ii = <722 = <733 = 1) метриче­ские коэффициенты взаимного базиса системы координат име­ют следующие значения:Я11 = 022 = S’33 = 1,д’3 =0,i/j.(1.35)В цилиндрической системе координат (<7ц = <733 = 1, <722 = т*2)метрические коэффициенты взаимного базиса отличаются откоэффициентов основного базиса:?1 = 1,g22 = l/r2,д33 = 1,gij = 0,(1.36)В заключение отметим, что существует еще один типметрических коэффициентов — метрические коэффициентысмешанного типа, которые определяются как скалярные про­изведения двух базисных векторов, один из которых принад­лежит к основному базису, а второй — к взаимному:приприi = 3.i ± 3-(1-37)Согласно определению взаимного базиса (1.32), значенияметрических коэффициентов д? обусловливаются значениямисимволов Кронекера 6?.

Совокупность девяти метрических ко­эффициентов смешанного типа образует метрическую матри­цу ( () , которая является диагональной единичной матри­цей:Таким образом, система координат в данной точке про­странства характеризуется тройкой векторов rj, Г2> г3, соста­вляющих основной базис, тройкой векторов г1, г2, г3, соста­вляющих взаимный базис, а также тремя метрическими ма­трицами, компонентами которых55являются метрические коэффициенты основного и взаимногобазисов, а также метрические коэффициенты смешанного ти­па.1.3.2.

Преобразования координати базисных векторовПри анализе характера математических объектов мате­матического аппарата механики сплошных сред было отме­чено, что основное требование, предъявляемое к указаннымобъектам, — их инвариантность относительно преобразова­ния системы координат. Такие математические объекты на­зываются тензорами. Простейшими тензорами являются ска­лярные величины, так как их значения не зависят от того,в какой системе координат (декартовой прямоугольной, ци­линдрической, сферической или какой-то другой) рассматри­вается движение сплошной среды.

Покажем, что векторныевеличины также инвариантны относительно преобразованиясистемы координат, т.е. не изменяются при переходе от однойсистемы координат к другой (при неизменности точки отсче­та).Для описания движения сплошной среды введем некото­рую систему координат х1 (ж1, х2, ж3), например декартовупрямоугольную систему координат (ж1 = х, х2 = у, ж3 = z).Выберем произвольную точку М пространства, положение ко­торой относительно точки 0 начала координат характеризует­ся радиус-вектором г, и сколь угодно близкую к точке М точкуЛ/1, положение которой относительно исходной точки харак­теризуется вектором dr (рис.

1.39). Для описания движениясплошной среды может быть выбрана и любая другая системакоординат у3 (т/1, у2, у3), например цилиндрическая системакоординат (у1 = г, у2 = в, у3 = z). Будем в дальнейшем длякраткости систему координат хг называть старой, а системукоординат у3 — новой. Предположим, что между координа­тами точек пространства в старой и новой системах коорди­нат существует взаимосвязь: хг = хг(у3), у3 = у3(хг>), т.е. ка­ждая из трех координат х1, х2, х3 зависит от трех координат56у1, У2, У* и наоборот.

Например, координаты точек простран­ства в декартовой прямоугольной и цилиндрической системахкоординат связаны известными соотношениями: х = rcos0,у — rsinfl, z — z.В системе координат х1 вектор dr может быть предста­влен в виде разложения по векторам основного базиса Т{ вточке М как сумма произведений векторов основного базисаи дифференциалов координат:дтdr — ——г dx1 — Т{ dxдх11’где дифференциалы координат dx1 являются компонентамивектора dr в разложении по векторам основного базиса (см.(1.22) и (1.23)).

При переходе от старой системы координатхг к новой системе координат у3 будут изменяться значениякомпонент вектора dr от dxz к dy а также будет изменять­ся и совокупность трех векторов, образующих.основной базиссистемы координат в данной точке пространства. В соответ­ствии с определением (1.20) векторы основного базиса будутизменяться от тг = дг/дх1 (векторы основного базиса в систе­ме координат хг) к (ту/ = дг/ду3 (векторы основного базиса всистеме координат у3).

Несмотря на изменение компонент век­тора dr и базисных векторов при переходе от одной системыкоординат к другой, сумма произведений компонент вектора57и соответствующих векторов основного базиса остается неиз­менной, т.е. вектор dr (как математический объект) являетсяинвариантным относительно преобразования системы коорди­нат:dr = гг dxl — (rj)f dy3.(1.38)Преобразование координат проводится по закону, но­сящему название контрвариантного закона преобразования.Согласно предположению относительно взаимосвязи междукоординатами старой и новой систем координат, каждая изтрех координат у1, у2, у$ зависит от трех координат ж1, ж2,х3:Компоненты вектора dr в новой системе координат у3 илидифференциалы ее координат определяются в соответствии справилами дифференцирования функции нескольких перемен­ных и соглашением о суммировании:Эти выражения могут быть записаны в общем видеСледовательно, чтобы перейти от компонент dxk вектора drв системе координат хг к компонентам dy3 этого же векторав системе,координат у3, необходимо знать частные производ­ные ду3/дхк новых координат по старым.

Среди алгебраических операций, приведённых в предыдущем параграфе, отсутствует широко используемая в векторном анализе операция скалярного произведения векторов. Напомним, что скалярное произведение векторов и , принадлежащих некоторому , определяется как операция, обладающая следующими свойствами:

А) инвариантности, то есть — скаляр;

Б) симметричности, то есть ;

В) билинейности, то есть и ;

Г) если для , то ; если для , то .

Часто требуют также, чтобы для любых скалярное произведение было положительным. От этого требования, сильно ограничивающего общность рассмотрения, мы откажемся.

Приведенные свойства скалярного произведения буквально повторяют свойства операции свёртывания (40) с той существенной разницей, что операция скалярного произведения определяется для двух элементов одного и того же , тогда как операция свёртывания задаётся для элементов, принадлежащих сопряжённым друг другу пространствам и . Естественно определить скалярное произведение с помощью свёртывания. Это можно сделать, если сопоставить каждому элементу некоторый элемент , то есть отобразить . Отображение должно быть, очевидно, линейным, чтобы не нарушалось свойство билинейности скалярного произведения.

Пусть задано невырожденное линейное отображение (преобразование) , то есть каждому поставлен в соответствие некоторый элемент . Тогда между компонентами и в каждом взаимном базисе имеет место связь:

, (1)

Где , поскольку отображение невырожденное.

Определим теперь скалярное произведение как свёрток одного из векторов ( или ) с соответствующим вектором ( или ) сопряжённого пространства, а именно:

. (2)

Записывая (2) в некотором взаимном базисе и используя (1), получим:

. (3)

Требование симметрии скалярного произведения

Приводит к условию

, (4)

То есть к симметрии .

Соотношение (3) определяет скалярное произведение векторов из . Для того, чтобы определить скалярное произведение векторов сопряжённого пространства , можно повторить (с необходимыми изменениями) соответствующие рассуждения.

Пусть задаёт обратное преобразование, то есть . Записывая это утверждение в некотором взаимном базисе, получим:

. (5)

Поскольку в результате последовательного выполнения отображений желательно, начиная с некоторого элемента , снова придти к этому же элементу (то есть ), то тензоры и должны быть взаимно обратными, то есть:

. (6)

Очевидно, что является симметричным контравариантным тензором валентности 2. Из-за связи (6) достаточно ввести один из тензоров или ; обычно задаётся ковариантный тензор .

Тензоры и называются Фундаментальными метрическими тензорами пространства (часто, не совсем правильно, их называют также Метрикой). Пространство, в котором введён метрический тензор, называется Метрическим.

Уравнения (1) и (5) устанавливают взаимно однозначное соответствие между контравариантными и ковариантными векторами. Соответствующие векторы мы будем обозначать одной и той же коренной буквой. Тем самым вводится ещё одна алгебраическая операция над тензорами – Операция поднятия и опускания индексов. Эту операцию мы будем применять не только к векторам, но и к тензорам произвольной валентности, придерживаясь того же принципа в обозначениях: тензоры, получаемые друг из друга путём свёртывания с метрическими тензорами, обозначаются одной и той же коренной буквой. Например:

, .

Метрический тензор определяется для определения Нормы вектора с помощью соотношения

. (7)

Следует иметь ввиду, что символ в этом соотношении не означает, что , так как квадратичная форма (7) вовсе не обязательно положительно определена. Использование этого символа и для неопределённых форм является данью традиции, сложившейся при использовании положительно определённых метрических тензоров.

Если квадратичная форма (7) положительно (отрицательно) определена, то пространство называется Евклидовым. Пространство с неопределённой квадратичной формой (7) называется Псевдоевклидовым. Важнейшим примеров псевдоевклидова пространства является 4-мерное пространство-время специальной теории относительности или пространство Минковского.

Соотношение (3) определяет скалярное произведение с помощью метрического тензора. Наоборот, если скалярное произведение векторов определено независимо, то с его помощью можно определить . Пусть известен способ определения скалярного произведения векторов (например, с помощью измерения длин и углов в модели полярных векторов). Рассмотрим скалярное произведение базисных векторов и . Записывая для него выражение типа (3), имеем:

, (9)

Где — -я компонента базисного вектора в этом же базисе. Вспомним, что любая компонента есть свёрток вектора с соответствующим вектором взаимного базиса. Тогда

.

Но поскольку базис по условию взаимен, то . Подставляя этот результат в (9), получаем:

, (10)

То есть компоненты ковариантного метрического тензора представляют собой скалярные произведения соответствующих базисных векторов.

Надлежащим выбором базиса в метрический тензор всегда может быть приведён к диагональному виду. Это значит, что скалярные произведения при . Если скалярное произведения двух векторов равно нулю, то обычно говорят, что эти векторы ортогональны. При этом пользуются следующим определением угла между векторами:

. (11)

(В случае неопределённой метрики этим соотношением этим соотношением следует пользоваться с осторожностью, так как может оказаться, что или , хотя ; соответствующие примеры рассмотрим ниже).

Базис, в котором при называется ортогональным; если, кроме того,

, (12)

То соответствующий базис называется ортонормированным.

Очевидно, что в евклидовом пространстве в ортонормированном базисе представляется единичной матрицей, то есть:

. (13)

Отсюда следует, что ортогональные компоненты (то есть отнесённые к ортонормированному базису) соответствующих друг другу ко- и контравариантных векторов совпадают между собой. Из-за того, что такие базисы наиболее часто используются на практике, нередко не подозревают о существовании двух различных типов векторов.

Рассмотрим подробнее пространство Минковского. В ортонормированном базисе метрический тензор имеет форму:

, (14)

(часто выбирают метрический тензор с противоположным знаком). Для вектора согласно (10), имеем . Векторы для которых , называют Временноподобными. Для каждого из базисных векторов () имеем: . Такие векторы называются Пространственноподобными. Векторы, для которых (при ), называются Изотропными (также нулевыми или светоподобными). Легко проверить, что к числу последних относится вектор . Если считать, что векторы и ортогональны в том случае, когда их скалярное произведение обращается в 0, то ясно, что каждый изотропный вектор ортогонален самому себе. Для изотропных векторов формула (11) неприменима.

По отношению к произвольным преобразованиям базиса вид (12) метрического тензора, разумеется, инвариантен. Преобразования, сохраняющие вид (12) метрического тензора, образуют подгруппу общей линейной однородной группы преобразований базиса и называются Ортогональными. Ортогональные непрерывные преобразования базиса в евклидовом пространстве представляют собой -мерные вращения. Ортогональные преобразования в пространстве Минковского называются преобразованиями Лоренца.

Онлайн калькулятор. Разложение вектора по базису.

Этот онлайн калькулятор позволит вам очень просто разложить вектор по базисным векторам.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач и закрепить пройденый материал.

Калькулятор для разложения вектора по базисным векторам

Выберите размерность пространства

Количество координат в векторе:

Введите значение базисных векторов:

Введите значение вектора, который необходимо разложить по базису:

Инструкция использования калькулятора для разложение вектора по базисным векторам

• Для того чтобы разложить вектор по базисным векторам онлайн:
• выберите необходимую вам размерность пространства (количество координат в векторе);
• введите значения базисных векторов;
• введите значения вектора который нужно разложить по базису;
• Нажмите кнопку «Разложить вектор по базису» и вы получите детальное решение задачи.

Ввод данных в калькулятор для разложение вектора по базисным векторам

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора разложение вектора по базисным векторам

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Теория. Разложение вектора по базису

Чтобы разложить, вектор b по базисным векторам a₁ , . a_n , необходимо найти коэффициенты x ₁, . x_n , при которых линейная комбинация векторов a₁ , . a_n равна вектору b .

Коэффициенты x ₁, . x_n будут координатами вектора b в базисе a₁ , . a_n .

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1

1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 — x 1 ) · e ( 1 ) + ( x

2 — x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 — x 2 ) , . . . , ( x

n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 — 1 1 3 2 — 5 2 1 — 3

1 — 1 1 0 5 — 8 0 3 — 5

1 — 1 1 0 5 — 8 0 0 — 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x

1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x

1 ∆ = — 1 — 1 = 1 ∆ x

2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x

2 ∆ = — 1 — 1 = 1 ∆ x

3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

Матрицу Х ищем по формуле:

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.