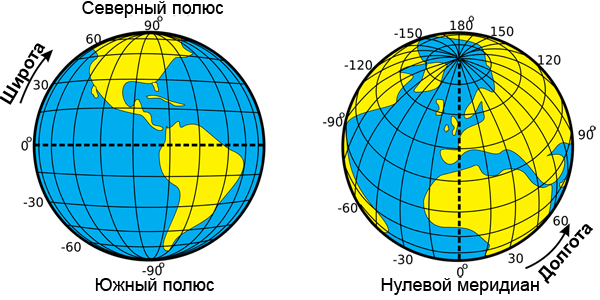
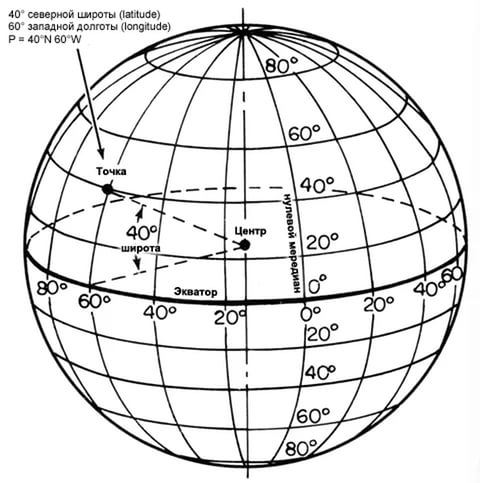
Географические координаты — это широта и долгота, которые определяют положение любой точки на Земле.
Координаты большинства пунктов на Земле имеют одновременно и широту, и долготу. Исключения — Северный и Южный полюсы. Географические полюса не имеют долготы, так как на полюсах сходятся все меридианы.
Географические координаты Северного полюса — (90°) с. ш., Южного полюса — (90°) ю. ш.
Определение географической широты
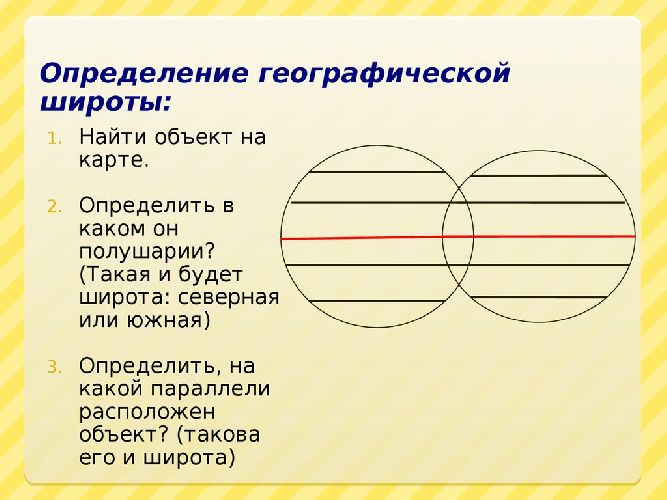
Чтобы определить географическую широту объекта, нужно определить полушарие и параллель, на которой он находится.
Пример:
«Северная столица» нашей страны город Санкт-Петербург находится севернее экватора на параллели (60°). Это значит, что его географическая широта равна (60°) с. ш. (северной широты).
На карте или глобусе невозможно показать все параллели. Для того чтобы более точно определить координаты нужного объекта, необходимо к широте ближайшей параллели со стороны экватора прибавить число градусов от этой параллели до нужного объекта.
Пример:
по карте мы видим, что Москва находится севернее экватора между параллелями (50°) и (60°). Число градусов между параллелью (50°) и столицей равно (6°). Значит географическая широта Москвы — (50° +) (6° =) (56°) с. ш. (северной широты).
Порядок определения географической широты:
-
найти географический объект на карте.
-
Определить полушарие, в котором расположен объект (Северное или Южное).
-
Определить (2) ближайшие параллели, между которыми расположен объект.
-
Определить шаг измерения: из большего значения параллели вычесть наименьшее.
-
Делим расстояние между обозначенными параллелями на столько частей, сколько получилось в предыдущем вычислении.
-
Определить параллель, на которой расположен объект.
Определение географической долготы
Чтобы определить географическую долготу объекта, нужно определить полушарие и меридиан, на котором он находится.
Если объект располагается между двумя меридианами, то порядок нахождения тот же, что и при определении широты, только находим меридианы и начинаем отсчёт от ближайшего к нулевому меридиану.
Пример:
Москва находится к востоку от меридиана (30°) на (8°). (30° +) (8° =) (38°) в. д.
Порядок определения географической долготы:
-
найти географический объект на карте.
-
Определить полушарие, в котором расположен объект (Западное или Восточное).
-
Определить (2) ближайших меридиана, между которыми расположен объект.
-
Определить шаг измерения: из большего значения меридиана вычесть наименьшее.
-
Делим расстояние между обозначенными меридианами на столько частей, сколько получилось в предыдущем вычислении.
-
Определить меридиан, на котором расположен объект.
Каждая точка поверхности планеты имеет определенное положение, которому соответствует собственная координата по широте и долготе. Она находится на пересечении сферических дуг меридиана, отвечающего за долготу, с параллелью, что соответствует широте. Обозначается парой угловых величин, выраженных в градусах, минутах, секундах, что имеет определение системы координат.
Широта и долгота — это географический аспект плоскости или сферы, перенесенный на топографические изображения. Для более точного нахождения какого-либо пункта берется во внимание также его высота над уровнем моря, что позволяет найти его в трехмерном пространстве.
Широта и долгота
Необходимость найти точку по координатам широты и долготы возникает по долгу службы и по роду занятий у спасателей, геологов, военных, моряков, археологов, летчиков и водителей, но может понадобиться и туристам, путешественникам, искателям, исследователям.
Что такое широта и как ее найти
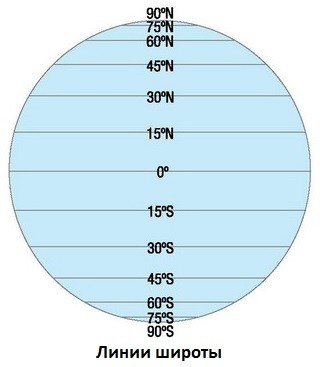
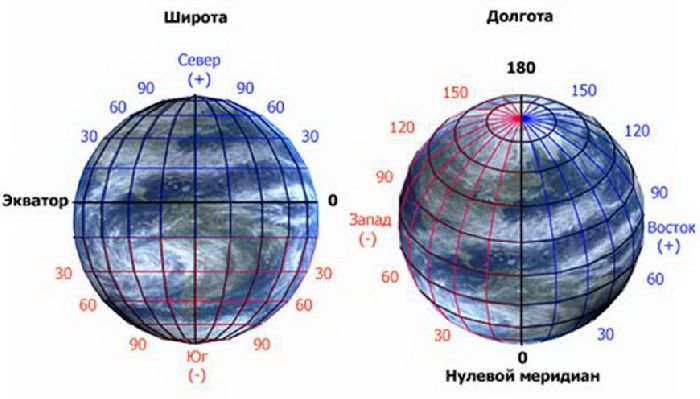
Широтой называют расстояние от объекта до линии экватора. Измеряется в угловых единицах (таких как градус, град, минута, секунда и т.д.). Широта на карте либо глобусе обозначается горизонтальными параллелями — линиями, описывающими окружность параллельно экватору и сходящимися в виде ряда сужающихся колец к полюсам.
Линии широты
Поэтому различают широту северную — это вся часть земной поверхности севернее экватора, а также южную — это вся часть поверхности планеты южнее экватора. Экватор — нулевая, самая длинная параллель.
- Параллели от линии экватора к северному полюсу принято считать положительной величиной от 0° до 90°, где 0° — это собственно сам экватор, а 90° — это вершина северного полюса. Они считаются как северная широта (с.ш.).
- Параллели, исходящие от экватора в сторону южного полюса, обозначены отрицательной величиной от 0° до -90°, где -90° — это место южного полюса. Они считаются как южная широта (ю.ш.).
- На глобусе параллели изображаются опоясывающими шар окружностями, которые уменьшаются с их приближением к полюсам.
- Все пункты на одной параллели будут обозначаться единой широтой, но различной долготой.
На картах, исходя из их масштаба, параллели имеют форму горизонтальных, изогнутых дугой, полос — чем меньше масштаб, тем прямее изображена полоса параллели, а чем крупнее — тем она более изогнута.
Запомните! Чем ближе к экватору располагается заданная местность, тем меньшей будет ее широта.
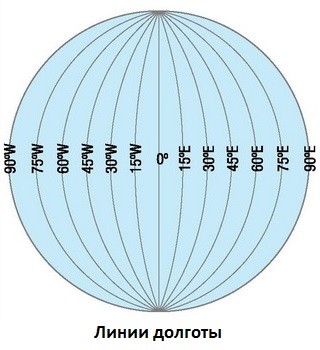
Что такое долгота и как ее найти
Долгота — это величина, на которую удалено положение заданной местности относительно Гринвича, то есть нулевого меридиана.
Линии долготы
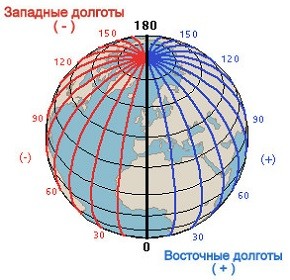
Долготе аналогично присуще измерение в угловых единицах, только с 0° до 180° и с приставкой — восточная либо западная.
- Нулевой меридиан Гринвича вертикально опоясывает шар Земли, проходя через оба полюса, разделяя его на западное и восточное полушария.
- Каждая из частей, находящихся к западу от Гринвича (в западном полушарии) , будет носить обозначение западной долготы (з.п.).
- Каждая из частей, удаленная от Гринвича на восток и расположенная в восточном полушарии, будет носить обозначение восточной долготы (в.п.).
- Нахождение каждой точки по одному меридиану имеют единую долготу, но различную широту.
- Меридианы нанесены на карты в виде вертикальных полос, изогнутых в форме дуги. Чем мельче масштаб карты, тем прямее будет полоса меридиана.
Запомните! Чем далее от Гринвича удаляется искомый пункт, тем большей будет его долгота, чем ближе — тем меньшей будет его долгота.
Как найти координаты заданной точки по карте
Зачастую приходится узнавать координаты пункта, который расположен на карте в квадрате между двумя ближайшими параллелями и меридианами. Приблизительные данные можно получить на глазок, оценив последовательно шаг в градусах между нанесенными на карту линиями в интересующем районе, а затем сопоставив удаленность от них искомой местности. Для точных вычислений понадобятся карандаш с линейкой, или же циркуль.
- За исходные данные берем обозначения ближайших к нашей точке параллели с меридианом.
- Далее смотрим шаг между их полосами в градусах.
- Потом смотрим величину их шага по карте в см.
- Измеряем линейкой в см расстояние от заданной точки до ближайшей параллели, а также расстояние между этой линией и соседней, переводим в градусы и берем во внимание разницу — вычитая от большей, либо прибавляя к меньшей.
- Таким образом получаем широту.
Пример! Расстояние между параллелями 40° и 50°, среди которых находится наша местность, составляет 2 см либо 20 мм, а шаг между ними — 10°. Соответственно, 1° равен 2 мм. Наша точка удалена от сороковой параллели на 0,5 см либо 5 мм. Находим градусы до нашей местности 5/2 = 2,5°, которые нужно прибавить к значению ближайшей параллели: 40° + 2,5° = 42,5° — это наша северная широта заданной точки. В южном полушарии вычисления аналогичны, но результат имеет отрицательный знак.
Аналогично находим долготу — если ближайший меридиан находится дальше от Гринвича, а заданный пункт ближе — то разницу вычитаем, если меридиан к Гринвичу ближе, а пункт дальше — то прибавляем.
Если под рукой нашелся только циркуль, то его его кончиками фиксируется каждый из отрезков, а распор переносится на масштаб.
Похожим образом производятся вычисления координат на поверхности глобуса.
Лучшие сервисы для поиска места по координатам
Проще всего узнать своё местоположение можно, зайдя в ПК-версию сервиса, работающего непосредственно с Google Maps. Многие утилиты упрощают процесс ввода широты и долготы в браузере. Рассмотрим лучшие из них.
Map & Directions
На официальном сайте Maps & Directions можно найти точные GPS-координаты любого пункта, или же выбрать нужное место и посмотреть его ширину и долготу. Пользоваться сервисом очень легко, в него включена опция увеличения масштаба на карте и возможность поделиться своим местоположением.
Кроме того, Maps & Directions позволяет бесплатно определить координаты своего положения на карте, нажав всего на одну кнопку. Щелкните на «Найти мои координаты», и сервис тут же поставит маркер и определит широту, долготу до многих тысячных, а также высоту.
На этом же сайте можно измерить расстояние между населенными пунктами или площадь любой заданной территории, нарисовать маршрут или рассчитать время передвижения. Сервис пригодится как путешественникам, так и просто любопытным пользователям.
Mapcoordinates.net
Полезная утилита Mapcoordinates.net позволяет узнать координату точки в любом регионе мира. Сервис также интегрирован с Google Картами, но обладает упрощенным интерфейсом, благодаря которому его сможет использовать даже неподготовленный пользователь.
В адресной строке утилиты, где написано «Искать», введите адрес места, широту и долготу которого Вы хотите получить. Карта с координатами появится вместе с маркером на нужном месте. Над маркером будет отображена широта, долгота, а также высота выбранной точки.
К сожалению, Mapcoordinates.net не подходит для того, чтобы искать пункты, зная их координаты. Однако для обратной процедуры это очень удобная утилита. Сервис поддерживает множество языков, в том числе и русский.
Поиск по координатам на карте через браузер с помощью сервиса Google Maps
Если по каким-либо причинам Вы предпочитаете работать не с упрощенными сервисами, а непосредственно с Google Maps, то эта инструкция будет полезной для Вас. Процесс поиска по координатам через Google Карты чуть более сложен, чем в описанных ранее способах, но им можно овладеть быстро и без особого труда.
Чтобы узнать точные координаты места, придерживайтесь следующей простой инструкции:
-
Откройте сервис на ПК. Важно, что должен быть включен полный, а не облегченный (отмечается специальным значком молнии) режим, иначе получить информацию не получится;
-
Щелкните на участок карты, где расположен нужный Вам пункт или точка, правой кнопкой мыши;
-
Отметьте в появившемся меню вариант «Что здесь?»;
-
Посмотрите на вкладку, которая отобразится внизу экрана. На ней будут отображены широта, долгота и высота.
Чтобы определить место по известным географическим координатам, потребуется другой порядок действий:
-
-
Откройте Google Карты в полном режиме на компьютере;
-
В строке поиска в верхней части экрана Вы можете ввести координаты. Сделать это допускается в следующих форматах: градусы, минуты и секунды; градусы и десятичные минуты; десятичные градусы;
-
-
Нажмите клавишу «Enter», и на карте на требуемом месте появится специальный маркер.
Важнее всего при использовании сервиса Google Maps правильно указывать географические координаты. Карты распознают только несколько форматов данных, поэтому обязательно учитывайте следующие правила ввода:
-
При вводе градусов используйте специальный символ, обозначающий его «°», а не «d»;
-
В качестве разделителя между целой и дробной частями необходимо использовать точку, а не запятую, иначе строка поиска не сможет выдать место;
-
Сначала указывается широта, затем — долгота. Первый параметр необходимо записывать в диапазоне от -90 до 90, второй — от -180 до 180.
Найти специальный символ на клавиатуре ПК затруднительно, да и чтобы придерживаться необходимого списка правил, нужно прикладывать достаточно много усилий. Гораздо проще пользоваться специальными утилитами — лучшие из них мы привели в разделе выше.
Нахождение места по широте и долготе на ОС Андроид
Нередко требуется найти место по координатам вдали от ноутбука или персонального компьютера. Выручит мобильное приложение Google Maps, работающее на платформе Андроид. Обычно оно используется для того, чтобы проложить маршрут или узнать график движения транспортных средств, однако программа подойдет и для нахождения местоположения пункта или точки.
Скачать приложение на на Андроид можно на официальной странице в Google Play. Оно доступно как на русском, так и на английском языках. После установки программы придерживайтесь следующей инструкции:
-
Откройте Google Maps на устройстве и дождитесь появления карты;
-
Найдите интересующее Вас место. Нажмите на него и держите до тех пор, пока не отобразится специальный маркер;
-
Вверху экрана появится вкладка с окном поиска и полными координатами места;
-
Если Вам нужно найти место по координатам, а не наоборот, то способ на мобильном устройстве ничем не отличается от своего аналога на ПК.
Мобильная версия сервиса, как и работающая на ПК, позволит детально изучить нужное место, узнать его точные координаты, или наоборот, распознать адрес по известным данным. Это — удобный способ как для дома, так и для дороги.
Post Views: 592
Как найти место по координатам?

4.3
Средняя оценка: 4.3
Всего получено оценок: 211.
4.3
Средняя оценка: 4.3
Всего получено оценок: 211.
Как найти место на карте по координатам? Этот вопрос интересует школьников и кажется им трудным. Если знать, что означает градусная сеть, что такое координаты, можно научиться этому действию.
Что такое градусная сеть?
Градусная или координатная сеть представляет собой линии на карте, либо параллельные экватору, либо соединяющие полюсы.
Линии, параллельные экватору, в географии называют параллелями, их величина различна. Самая длинная параллель находится на равном расстоянии от полюсов, это экватор. От него начинается отсчет в сторону полюсов – от 0 до 90°. На картах изображаются не все параллели, чаще всего каждая десятая или тридцатая.
Линии, соединяющие полюсы, называют меридианами, их длина одинакова. На международных конгрессах за начальный меридиан договорились считать тот, что проходит через Гринвичскую обсерваторию вблизи Лондона. Отсчет ведется от 0 до 180°.
До конца XIX века страны пользовались собственным нулевым меридианом; в России он проходил через Пулковскую обсерваторию под Санкт-Петербургом.
Что такое географические координаты?
Географические координаты показывают расстояние объекта от экватора и Гринвичского меридиана, выраженные в градусах, определяемые отдельно в Северном и Южном полушариях, а также их восточной и западной части.
По параллелям находят широту, северную и южную (сокращенно с.ш. и ю.ш.). По меридианам определяют долготу, западную и восточную (сокращенно з.д. и в.д.).
Как найти место по координатам?
Зная координаты, нужно искать на карте соответствующие параллель и меридиан. Например, требуется найти город с координатами 56°с.ш., 38°в.д. Этот населенный пункт расположен в Северном полушарии, в его восточной части. Для определения широты находим 50-ю и 60-ю параллели, делим отрезок между ними на 10 частей и отсчитываем 56-ю параллель.
Для нахождения долготы ищем 30-й и 40-й меридиан, делим отрезок на 10 частей, отсчитываем 38-й меридиан.
Смотрим, где найденные линии пересекаются на карте и читаем название города. В нашем случае это Москва.
На картах следует читать указания, подписанные с двух сторон от нулевого меридиана (к западу или востоку от Гринвича); нужно помнить, что к северу от экватора считается северная широта, к югу от него южная.
На некоторых картах отрезки между параллелями и меридианами разбиты на градусы. Такие «линейки» для параллелей расположены на рамках карт, для меридианов на линии экватора.
Что мы узнали?
Мы узнали, для чего нужна градусная (координатная) сеть, что такое широта и долгота и как они записываются. Мы познакомились с порядком определения нужных параллелей и меридианов, узнали, где можно найти подсказку на карте. Мы выяснили, как найти место по координатам на любой карте.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Вадим Гаврин
5/5
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 211.
А какая ваша оценка?
Найти медиану треугольника по координатам вершин
Как найти медиану если даны координаты вершин треугольника?
Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.
Рассмотрим нахождение медианы на конкретном примере.

A(-11;12), B(3;8), C(-1;6),
AF — медиана.
Найти: AF
Решение:
1) Так как AF — медиана треугольника ABC, то F — середина BC.
По формулам координат середины отрезка:
Итак, F(1;7).
2) По формуле расстояния между точками
Ответ: 13.
Помогите доказать методом координат. Самостоятельная работа 4. Вариант 7. № 1 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс
Помогите доказать методом координат. Самостоятельная работа 4. Вариант 7. № 1 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс
Интересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Докажите методом координат, что медианы треугольника
пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин треугольника.
ответы
Пусть А(0; 0), В(b; h), С(а; 0). Пусть BE медиана и
Рассмотрим медиану АF и точку М1 на ней такую, что
=> М и М1 совпадают. Аналогично и с медианой CG. Ч.т.д.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19.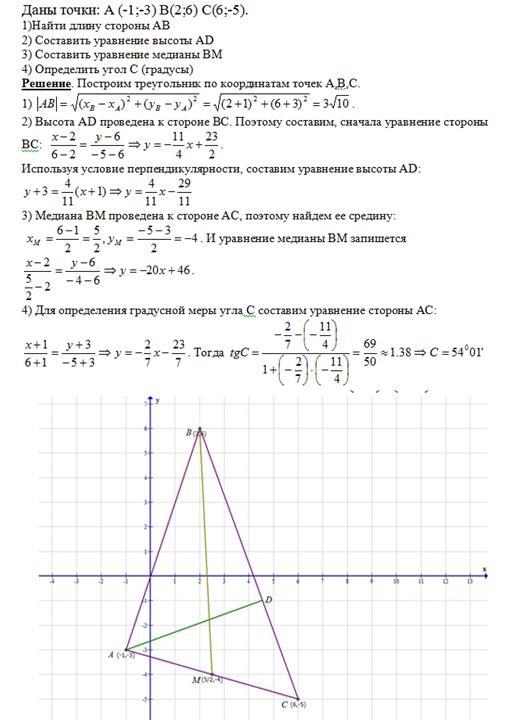
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Дадут ли аттестат после второй пересдачи.?
Мне сказала подруга,что аттестат не дадут после второй пересдачи,дадут только справку и всё,так ли это?
9 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
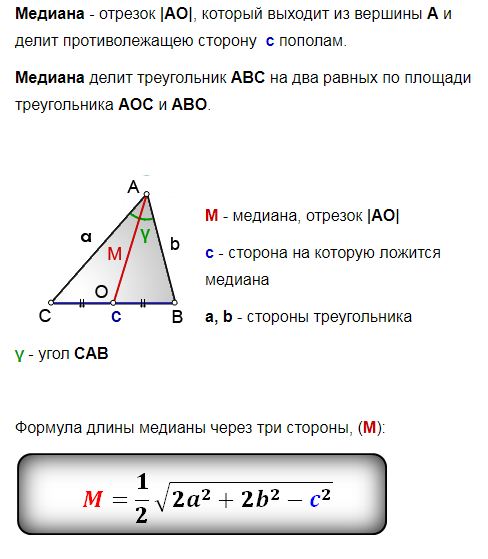
Как найти медиану треугольника зная его стороны.
Медиана и высота треугольника – это одна из самых увлекательных и интересных тем геометрии. Термин «Медиана» означает прямую или отрезок, который соединяет вершину треугольника с его противоположной стороной. Другими словами, медиана – это линия, которая проходит из середины одной стороны треугольника в противоположную вершину этого же треугольника. Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.
Свойства медианы треугольника
- Все медианы треугольника пересекаются в одной точке и разделяются этой точкой в соотношении 2:1, считая от вершины. Таким образом, если нарисовать в треугольнике все три медианы, то точка их пересечения будет делить их на две части. Часть, которая располагается ближе в вершине, будет составлять 2/3 всей линии, а часть, которая располагается ближе к стороне треугольника – 1/3 линии. Пересекаются медианы в одной точке.
- Три медианы, проведенные в одном треугольнике, делят этот треугольник на 6 маленьких треугольников, чья площадь будет равна.
- Чем больше сторона треугольника, от которой исходит медиана, тем меньше эта медиана. И наоборот, самая короткая сторона имеет самую длинную медиану.
- Медиана в прямоугольном треугольнике имеет ряд собственных характеристик. Например, если вокруг такого треугольника описать окружность, которая будет проходить через все вершины, то медиана прямого угла, проведенная к гипотенузе, станет радиусом описанной окружности (то есть ее длина будет составлять расстояние от любой точки окружности до ее центра).
Уравнение длины медианы треугольника
Формула медианы исходит из теоремы Стюарта и гласит, что медиана – это квадратный корень из отношения квадратов суммы сторон треугольника, которые образуют вершину, за вычетом квадрата стороны, к которой проведена медиана к четырем. Другими словами, чтобы узнать длину медианы нужно возвести в квадрат показатели длины каждой стороны треугольника, а затем записать это в виде дроби, в числителе которой будет сумма квадратов сторон, которые образуют угол, откуда исходит медиана, минус квадрат третьей стороны.
Точка пересечения медиан треугольника
Как мы писали выше, всем медианы одного треугольника пересекаются в одной точке. Эту точку называют центром треугольника. Он делит каждую медиану на две части, длина которым соотносится как 2:1. При этом центр треугольника является и центром описанной вокруг него окружности. А другие геометрические фигуры имеют собственные центры.
Координаты точки пересечения медиан треугольника
Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x 1 ;y 1), B(x 2 ;y 2), C(x 3 ;y 3),
и вычисляем координаты центра треугольника по формуле: x 0 = (x 1 + x 2 + x 3)/3; y 0 = (y 1 + y 2 + y 3)/3.
Площадь треугольника через медиану
Все медианы одного треугольника делят этот треугольник на 6 равных треугольников, а центр треугольника делит каждую медиану в соотношении 2:1.
Медианой именуется отрезок, проведенный из вершины треугольника на середину противоположной стороны, то есть делит ее точкой пересечения пополам. Точка, в которой медиана пересекает противоположную вершине, из которой она выходит, сторону, именуется основанием. Через одну точку, называемую точкой пересечения, проходит каждая медиана треугольника. Формула длины ее может выражаться несколькими способами.
Формулы для выражения длины медианы
- Зачастую в задачах по геометрии ученикам приходится иметь дело с таким отрезком, как медиана треугольника. Формула ее длины выражается через стороны:
где a, b и c — стороны. Причем с является стороной, на которую медиана опускается. Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов.
- Если при расчете известны две стороны треугольника и определенный угол α, находящийся между ними, то длина медианы треугольника, опущенной к третьей стороне, будет выражаться так.
Основные свойства
- Все медианы имеют одну общую точку пересечения O и ею же делятся в отношении два к одному, если вести отсчет от вершины. Такая точка носит название центра тяжести треугольника.
- Медиана разделяет треугольник на два других, площади которых равны. Такие треугольники называются равновеликими.
- Если провести все медианы, то треугольник будет разделен на 6 равновеликих фигур, которые также будут треугольниками.
- Если в треугольнике все три стороны равны, то в нем каждая из медиан будет также высотой и биссектрисой, то есть перпендикулярна той стороне, к которой она проведена, и делит надвое угол, из которого она выходит.
- В равнобедренном треугольнике медиана, опущенная из вершины, которая находится напротив стороны, не равной никакой другой, будет также высотой и биссектрисой.
Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности. - Если треугольник является основанием правильной пирамиды, то высота, опущенная на данное основание, проецируется в точку пересечения всех медиан.
- В прямоугольном треугольнике медиана, проведенная к наибольшей стороне, равняется половине ее длины.
- Пусть O — точка пересечения медиан треугольника. Формула, приведенная ниже, будет верная для любой точки M.
- Еще одним свойством обладает медиана треугольника. Формула квадрата ее длины через квадраты сторон представлена ниже.
Свойства сторон, к которым проведена медиана
- Если соединить любые две точки пересечения медиан со сторонами, на которые они опущены, то полученный отрезок будет являться средней линией треугольника и составлять одну вторую от стороны треугольника, с которой она не имеет общих точек.
- Основания высот и медиан в треугольнике, а также середины отрезков, соединяющих вершины треугольника с точкой пересечения высот, лежат на одной окружности.
В заключение логично сказать, что одним из самых важных отрезков является именно медиана треугольника. Формула ее может использоваться при нахождении длин других его сторон.
Медиана треугольника
— это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).
3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Длина медианы проведенной к стороне:
(док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )
Т1.
Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника.
СС 1 , АА 1 , ВВ
1 — медианы
∆ABC
. Доказать: и
Д-во: Пусть М — точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 — середину отрезка AM и С 2 — середину отрезка СМ. Тогда A 2 C 2 — средняя линия треугольника АМС.
Значит,А 2 С 2
|| АС
и A 2 C 2 = 0,5*АС. С 1
А 1
— средняя линия треугольника ABC. Значит, А 1
С 1
|| АС и А 1
С 1
= 0,5*АС.
Четырехугольник А 2 С 1 А 1 С 2
— параллелограмм, так как его противоположные стороны А
1
С 1
и А 2 С 2
равны и параллельны. Следовательно, А 2 М =
МА 1
и С 2 М =
МC 1 .
Это означает, что точки А 2
и M
делят медиану АА 2
на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1
. Итак, точка М пересечения двух медиан АА 2
и CC 2
треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника.
На медиане АА 1 такой точкой является точка М, следовательно, точка М
и есть точка пересечения медиан АА 1 иBB 1.
Таким образом, n
T2.
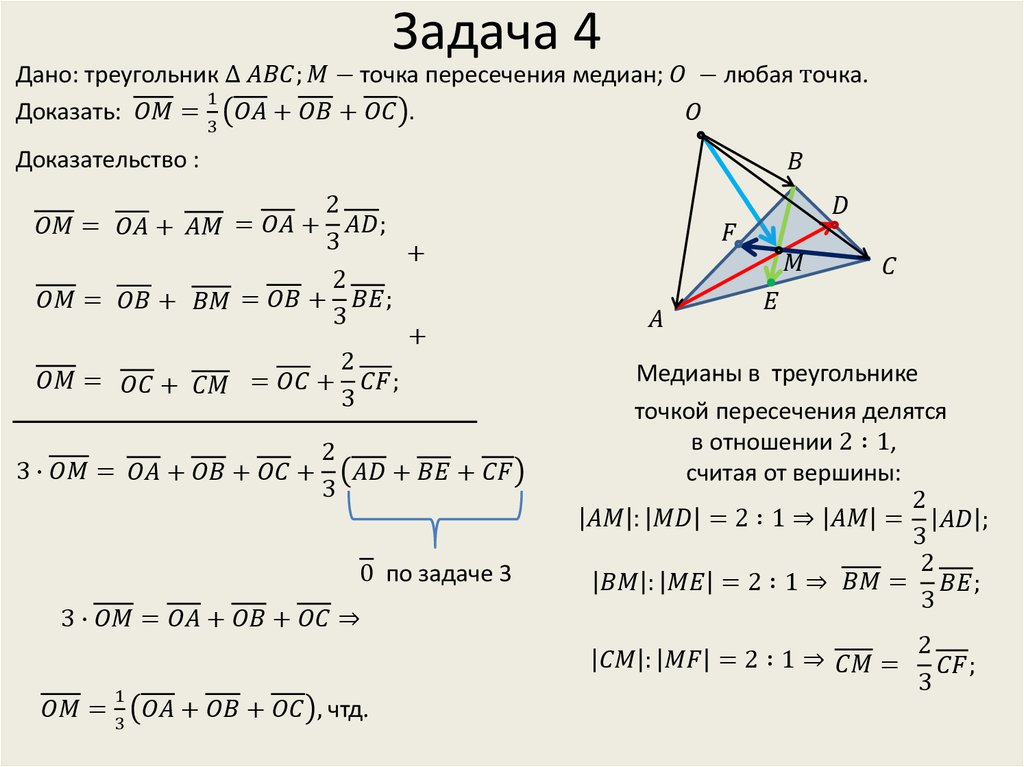
Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.
Доказать:S AMB
=S BMC
=S AMC .
Доказательство.
В,
у них общая. т.к. равны их основания и высота, проведенная из вершины М,
у них общая. Тогда
Аналогичным образом доказывается, чтоS AMB = S AMC .
Таким образом,S AMB = S AMC = S CMB .
n
Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис
Биссектриса угла
— луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.
Свойства
1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).
Вычисление длины биссектрисы
l c — длина биссектрисы, проведённой к стороне c,
a,b,c — стороны треугольника против вершин A,B,C соответственно,
p — полупериметр треугольника,
a l ,b l — длины отрезков, на которые биссектриса l c делит сторону c,
α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,
h c — высота треугольника, опущенная на сторону c.
Метод площадей.
Характеристика метода.
Из названия следует, что главным объектом данного метода является площадь.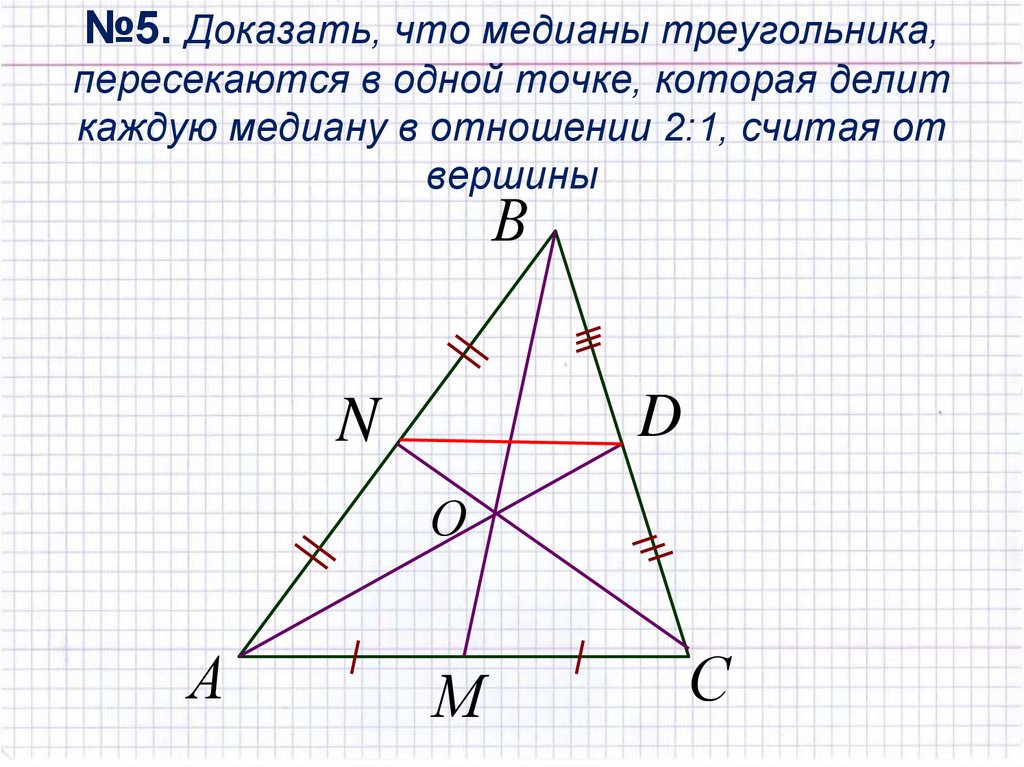
1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур
2) Метод отношения S: основан на след опорных задачах:
Теорема Чевы
Пусть точки A»,B»,C» лежат на прямых BC,CA,AB треугольника. Прямые AA»,BB»,CC» пересекаются в одной точке тогда и только тогда, когда
Доказательство.
Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см.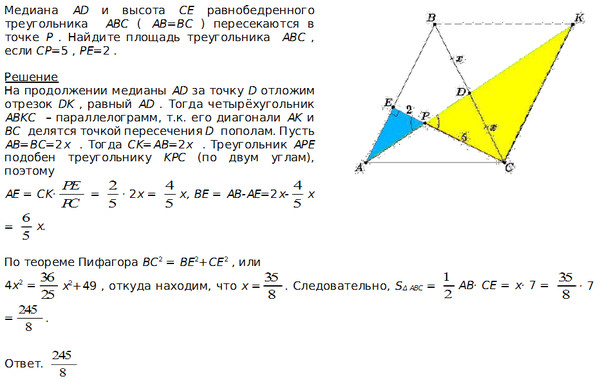
Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:
Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.
Аналогично получаем и
Перемножим эти три равенства:
что и требовалось доказать.
Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.
Теорема (обратная теорема Чевы)
. Пусть точки A»,B»,C» лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение
Тогда отрезки AA»,BB»,CC» и пересекаются в одной точке.
Теорема Менелая
Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда
Доказательство
.
ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно,
ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,
Из каждого равенства выразим CK:
Откуда что и требовалось доказать.
Теорема (обратная теорема Менелая).
Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение
Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.
Высоты Медианы и биссектрисы углов
Точно так же, как существуют специальные имена для особых типов треугольников, существуют специальные имена для особых отрезков внутри треугольников. Разве это не особенное?
База и высота
Каждый треугольник имеет три оснований (любая из его сторон) и три высот (высот).
Рисунок 1 Три основания и три высоты одного и того же треугольника.
Высоты иногда могут совпадать со стороной треугольника или иногда могут пересекаться с расширенным основанием за пределами треугольника. На рисунке 2 AC — это высота основания BC , а BC — высота основания AC .
Рисунок 2 В прямоугольном треугольнике каждый катет может служить высотой.
На рис. 3, AM — высота до базы BC .
Рисунок 3 Высота тупоугольного треугольника.
Интересно отметить, что в любом треугольнике три прямые, содержащие высоты, пересекаются в одной точке (рис. 4).
Рисунок 4 Три линии, содержащие высоты, пересекаются в одной точке,
, который может быть или не быть внутри треугольника.
Медиана
А медиана в треугольнике — это отрезок, проведенный от вершины к середине противоположной стороны. Каждый треугольник имеет три медианы. На рисунке 5 E является средней точкой BC . Следовательно, БЭ = ЭК . AE является медианой Δ ABC.
Рисунок 5 Медиана треугольника.
В каждом треугольнике три медианы сходятся в одной точке внутри треугольника (рис. 6).
Рисунок 6 Три медианы сходятся в одной точке внутри треугольника.
Биссектриса угла
Биссектриса угла в треугольнике — это отрезок, проведенный из вершины, которая делит пополам (разрезает пополам) этот угол при вершине. У каждого треугольника есть три биссектрисы угла. На рисунке , представляет собой биссектрису угла в Δ ABC.
Рисунок 7 Биссектриса угла.
В каждом треугольнике три биссектрисы угла пересекаются в одной точке внутри треугольника (рис. 8).
Рисунок 8 Биссектрисы трех углов пересекаются в одной точке внутри треугольника.
Как правило, высоты, медианы и биссектрисы являются разными отрезками. Однако в некоторых треугольниках они могут быть одними и теми же сегментами. На рисунке можно доказать, что высота, проведенная из угла при вершине равнобедренного треугольника, является медианой, а также биссектрисой угла.
Рисунок 9 Высота, проведенная из угла при вершине равнобедренного треугольника.
Пример 1: На основании маркировки на рисунке 10 назовите высоту Δ QRS, назовите медиану Δ QRS, и назовите биссектрису угла Δ QRS .
Рисунок 10 Нахождение высоты, медианы и биссектрисы угла.
RT является высотой до основания QS , потому что RT ⊥ QS .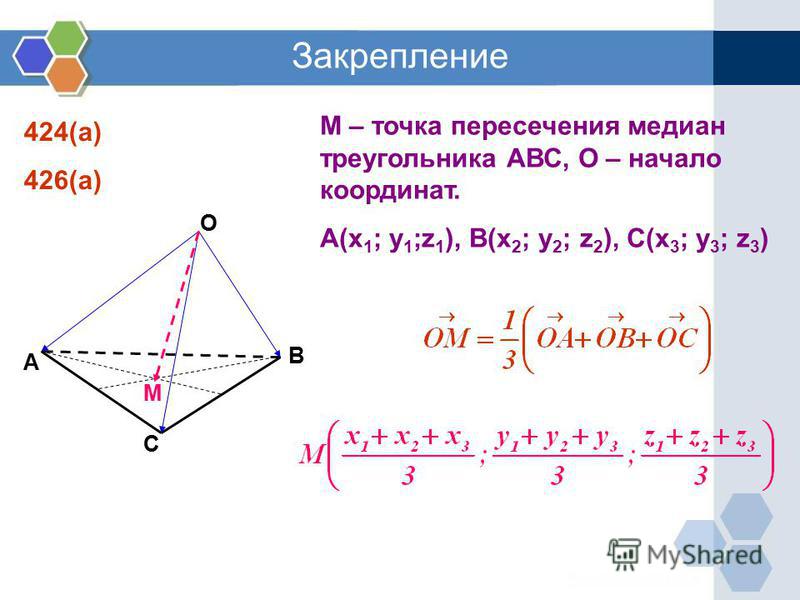
SP является медианой базы QR , поскольку P является средней точкой QR .
QU является биссектрисой угла Δ QRS , поскольку делит пополам ∠ RQS.
Калькулятор формул для уравнений равнобедренного треугольника
Изменить уравнение
Выберите, чтобы найти другое неизвестное
Разносторонний треугольник:
Стороны не имеют одинаковой длины
Нет равных углов
Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника. Сокращенные
уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.
| Perimeter | |
| Semiperimeter | |
| Area | |
| Area | |
| Base | |
| Height | |
| Angle Bisector стороны a | |
| Биссектриса угла стороны b | |
| Биссектриса угла стороны c | |
| Median of side a | |
| Median of side b | |
| Median of side c | |
| Altitude of side a | |
| Altitude of side b | |
| Высота стороны c | |
| Радиус описанной окружности | |
| Радиусы вписанной окружности |
9 20003 .
| Длина стороны A | |
| Периметр | |
| Полупериметр | |
| Площадь | |
| Высота 6 | |
| Median | |
| Angle Bisector | |
| Circumscribed Circle Radius | |
| Inscribed Circle Radius |
Right Triangle:
One angle is equal to 90 degrees
Уравнения прямоугольного треугольника
| Теорема Пифагора | |
| Периметр | |
| Semiperimeter | |
| Area | |
| Altitude of a | |
| Altitude of b | |
| Altitude of c | |
| Angle Bisector of a | |
| Биссектриса угла b | |
| Биссектриса угла c | |
| Медиана |
| Median of b | |
| Median of c | |
| Inscribed Circle Radius | |
| Circumscribed Circle Radius |
7
Isosceles Triangle:
Two sides have equal length
Two angles are равно
Уравнения равнобедренного треугольника
| Периметр | ||||
| Полупериметр | ||||
| Area | ||||
| Altitudes of sides a and c | ||||
| Altitude of side b | ||||
| Median of sides a and c | ||||
| Median of side b | ||||
| Биссектриса угла сторон a и c | ||||
| Биссектриса угла стороны b | ||||
| Радиус описанной окружности | 9167 | 0169 | Inscribed Circle Radius |
Where
= = .
| P | = | Perimeter |
| s | = | Semiperimeter |
| a | = | Length of side a |
| b | = | Длина стороны b |
| c | = | Длина стороны c |
| h | 9016 Высота над уровнем моря0172 | |
| m | = | Median |
| A | = | Angle A |
| B | = | Angle B |
| C | = | Angle C |
| T | = | Угол бисектор |
| R | = | RIGHTRED RADIUS |
| R | ||
| R | ||
| R | ||
| R | ||
| R | = | |
| R | = | |
| r | = | |
| r | = |