Как найти матрицу пути графа

Матрица путей

Для
связного графа, вершины которого
перенумерованы, можно построить
матрицу путей (или цепей) Р
следующим
образом: строки матрицы должны
соответствовать путям из первой вершины
в последнюю, а столбцы – ребрам графа.
Следовательно, элемент матрицы
принимает значение 1 или 0 в зависимости
от того, принадлежит ли данное ребро
данному пути или нет. Например, граф,
изображенный на рис. 11, имеет матрицу
путей между вершинами v₁
и v₅:

Рис.11.
Граф для иллюстрации матрицы путей

Представление графов в виде списков

Можно
связать список L_v
с
каждой вершиной
v
V.
Таким образом, L_v
– это список вершин, смежных с v
(например, рис.12).

Возможно
другое представление графов с помощью
списка связей. Выбор представления
зависит от используемых алгоритмов.

а) б)

Рис.
12. Полный граф (а) и его списки смежности
(б)

Упорядоченные графы

Представление
L_v
вершин, смежных с v,
в виде списка связей определяет «порядок»
ребер, выходящих из v
(рис. 13).

v₁

Рис.
13. Пример упорядоченного графа

Множество
V
= {v₁,
v₂,…,
v_n}
вершин вместе с множеством {Lv₁,
Lv₂,
…, Lv_n}
упорядоченных списков упорядоченных
пар вершин называют упорядоченным
графом.

Для
того чтобы рассматриваемые структуры
являлись графами, необходимо наложить
некоторые условия на списки Lv:

(v,
v)
Lv
, v
V;
(w,
u) Lw (u, w) Lu.

Граф,
изображенный на рис. 13, может быть
представлен в терминах упорядоченного
графа следующим образом:

({v1,
v2,
v3,
v4},
{((v1,
v2),
(v1,
v3),
(v1,
v4)),
((v2,
v1),
(v2,
v3),
(v2,
v4)),
((v3,
v1),
(v3,
v2),
(v3,
v4)),
((v4,
v1),
(v4,
v2),
(v4,
v3))}).

Упорядоченный
граф определяет единственный
неупорядоченный граф. Обратное утверждение
неверно, так как в общем случае возможно
много способов упорядочения графа.

Задачи нахождения путей в графах

Пусть
G
= (V,
E)
– ориентированный граф.

Рефлексивным
и транзитивным замыканием графа G
называется граф G^*,
который содержит то же множество узлов,
что и G,
но в котором из v
в w
идет ребро тогда и только тогда, когда
в G
существует путь (длины 0 или больше) из
v
в w.

С
задачей нахождения транзитивного
замыкания тесно связана задача о
кратчайшем пути.

Поставим
в соответствие каждому ребру e
графа G
= (V, E)
неотрицательную стоимость c(e).
Стоимость пути определяется как сумма
стоимостей ребер, образующих этот путь.
Задача о кратчайшем пути состоит в
нахождении для каждой пары узлов (v,
w)
пути наименьшей стоимости среди всех
путей из v
в w.

Наряду
с понятием стоимости пути применяется
понятие метки пути. Определим метку
пути как произведение меток ребер,
составляющих этот путь. Причем метки
берутся в порядке прохождения ребер. В
частности, метка пути нулевой длины
равна 1. Для каждой пары узлов (v,
w)
определим c(v,
w)
как сумму меток всех путей между v
и w.
Назовем c(v,
w)
стоимостью прохождения из v
в w.

Например,
рассмотрим ориентированный граф, в
котором каждое ребро помечено элементом
полукольца S1
= ({0, 1}, +, , 0, 1)
(рис. 14).

Метка
пути v₁,
v₂,
v₃,
равна 1. Простой цикл из v₂
в v₂
имеет метку 1 0 = 0. Вообще, каждый путь
положительной длины имеет метку 0. Но
стоимость пути нулевой длины из v₂
в
v₂
равна 1. Следовательно, c(v₂,
v₂)=
1.

Рис.
14. Метка пути и стоимость пути

Соседние файлы в папке Структуры и алгоритмы

Источник

Нахождение множества вершин, входящих в путь

Если необходимо узнать о вершинах графа, входящих в эти пути, то следует вспомнить определения прямого и обратного транзитивных замыканий. Так как T⁺(x_i) – это множество вершин, в которые есть пути из вершины x_i, а T^–(х_j) – множество вершин, из которых есть пути в x_j, то $T^{+}(x_{i}) cap T^{–}(x_{j})$ – множество вершин, каждая из которых принадлежит, по крайней мере, одному пути, идущему от x_i к x_j. Эти вершины называются существенными или неотъемлемыми относительно двух концевых вершин x_i и x_j. Все остальные вершины графа называются несущественными или избыточными, поскольку их удаление не влияет на пути от x_i к x_j.

Рис.
4.2.
Орграф

Так для графа на
рис.
4.2
нахождение вершин, входящих в путь, например из вершины х₂ в вершину х₄, сводится к нахождению $Т^{+}( х_{2}) ={ х_{2}, x_{3}, х_{4}, х_{5}, х_{6}} , Т^{-}( х_{4}) ={ х_{1}, х_{2}, x_{3}, х_{4}, х_{5}} , и их пересечения T^{+}(х_{2}) cap T^{–}(х_{4}) ={ х_{2}, x_{3}, х_{4}, х_{5}}$ .

Матричный метод нахождения
путей в графах

Матрица смежности полностью определяет структуру графа. Возведем матрицу смежности в квадрат по правилам математики. Каждый элемент матрицы А²
определяется по формуле

$a^{(2)}_{ik}= sum ^{n}_{j=1}a_{ij}a_{jk}$

Слагаемое в формуле равно 1 тогда и только тогда, когда оба числа a_ij
и a_jk
равны 1, в противном случае оно равно 0. Поскольку из равенства a_ij = a_jk = 1 следует существование пути длины 2 из вершины x_i
в вершину х_k
, проходящего через вершину x_j
, то
( i -й, k -й) элемент матрицы А²
равен числу путей длины 2, идущих из x_i
в х_k
.

На таблице 4.1a представлена матрица смежности графа, изображенного на
рис.
4.2. Результат возведения матрицы смежности в квадрат А²
показан на таблице 4.1б.

Таблица
4.1а.

		X₁	X₂	X₃	X₄	X₅	X₆
	X₁	0	1	0	0	0	1
	X₂	0	0	0	0	1	1
A=	X₃	0	1	0	0	1	1
	X₄	0	0	1	0	0	0
	X₅	0	0	0	1	0	1
	X₆	0	0	0	0	0	0

Таблица
4.1б.

		X₁	X₂	X₃	X₄	X₅	X₆
	X₁	0	0	0	0	1	1
	X₂	0	0	0	1	0	1
A²=	X₃	0	0	0	1	1	2
	X₄	0	1	0	0	1	1
	X₅	0	0	1	0	0	0
	X₆	0	0	0	0	0	0

Таблица
4.1в.

		X₁	X₂	X₃	X₄	X₅	X₆
	X₁	0	0	0	1	0	1
	X₂	0	0	1	0	0	0
A³=	X₃	0	0	1	1	0	1
	X₄	0	0	0	1	1	2
	X₅	0	1	0	0	1	1
	X₆	0	0	0	0	0	0

Таблица
4.1г.

		X₁	X₂	X₃	X₄	X₅	X₆
	X₁	0	0	1	0	0	0
	X₂	0	1	0	0	1	1
A⁴=	X₃	0	1	1	0	1	1
	X₄	0	0	1	1	0	1
	X₅	0	0	0	1	1	2
	X₆	0	0	0	0	0	0

Так «1», стоящая на пересечении второй строки и четвертого столбца, говорит о существовании одного пути длиной 2 из вершины х₂
к вершине х₄
. Действительно, как видим в графе на
рис.
4.2, существует такой путь: a₆, a₅
. «2» в матрице A2 говорит о существовании двух путей длиной 2 от вершины х₃
к вершине х₆ : a₈, a₄ и a₁₀, a₃
.

Аналогично для матрицы смежности, возведенной в третью степень A3 (
таблица
4.1в), a ⁽³⁾
_ik
равно числу путей длиной 3, идущих от x_i к х_k
. Из четвертой строки матрицы A3 видно, что пути длиной 3 существуют: один из х₄
в х₄(a₉, a₈, a₅), один из х₄ в х₅(a₉, a₁₀, a₆) и два пути из х₄ в х₆(a₉, a₁₀, a₃
и a₉, a₈, a₄). Матрица A₄ показывает существование путей длиной 4 (
таблица
4.1г).

Таким образом, если a ^р
_ik
является элементом матрицы A^р
,то a ^р
_ik
равно числу путей (не обязательно орцепей или простых орцепей) длины р, идущих от x_i
к х_k
.

Источник

Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

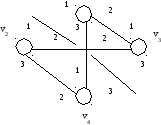
3.2. Морфология графа

Пути и контуры в графе

Сама матрица смежности A(Г₀) дает число путей, длина которых равна единице. Квадрат матрицы смежности
A²(Г₀) дает число путей, длина которых равна двум дугам. Куб матрицы
A³(Г₀) дает число путей в три дуги и т.д. В частности, на пересечении 2-го столбца и 3-ей строки матрицы
A³(Г₀) стоит 3. Это означает, что из вершины 3 в вершину 2 имеется три пути, а из вершины 2 в вершину 3 существует уже четыре пути в три дуги:

A²(Г₀) =
,     A³(Г₀) =
,

A⁴(Г₀) =
,
A⁵(Г₀) =
.

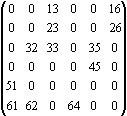
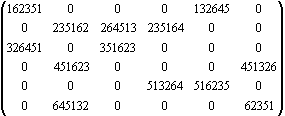
Введем понятие об означенной матрице смежности
A(Г₀), в которой вместо единиц выставляются соответствующие вершины (новое обозначение для этой матрицы вводить не станем). Вспомогательная матрица
A’(Г₀), получается из A(Г₀) путем отбрасывания первого символа в означенных дугах.

A(Г₀) =
,
A’(Г₀) =
.

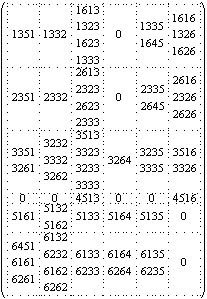
Матрица A’(Г₀) нужна для получения соответствующей степени матрицы A(Г₀). Так,

A(Г₀) · A’(Г₀) = A²(Г₀),
A²(Г₀) · A’(Г₀) =
A³(Г₀), …

В чем преимущество означенной матрицы перед матрицей смежности? Означенная матрица Aⁿ помимо числа путей указывает еще и вершины, через которые эти пути пролегают. На диагонали матрицы Aⁿ будут указаны всевозможные контуры, длина которых равна 1, 2, 3 и т.д. дугам. Неповторяющиеся вершины для отдельных путей укажут на
элементарные пути. Так как в нашем графе
Г₀ (рис. 3.14) имеется шесть вершин, то элементарных путей, длина которых равнялась бы шести дугам, вообще быть не может. Отсюда максимальная степень означенной матрицы для определения всех
гамильтоновых путей должна быть равна пяти. В нашем графе
Г₀, как на то указывает матрица A⁵(Г₀), только три гамильтоновых пути:
{3, 2, 6, 4, 5, 1}; {4, 5, 1, 6, 2, 3} и {2, 3, 5, 1, 6, 4}. На диагонали матрицы
A⁶(Г₀) стоит один и тот же гамильтонов контур
{1, 3, 2, 6, 4, 5, 1}, который всякий раз начинается с новой вершины.

A²(Г₀) =
A(Г₀) · A’(Г₀) =
,

A³(Г₀) = A²(Г₀) · A’(Г₀) =
.

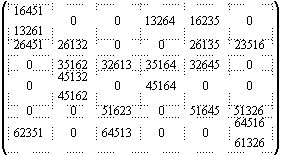
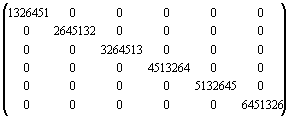
При получении следующих степеней означенных матриц оставим только гамильтоновы пути и контуры:

A⁴(Г₀) =
,

A⁵(Г₀) =
,

A⁶(Г₀) =
.