Аннотация: Рассматриваются вопросы достижимости для орграфов и способы нахождения матриц достижимости и контрдостижимости. Рассматривается матричный способ нахождения количества путей между любыми вершинами графа, а также нахождение множества вершин, входящих в путь между парой вершин. Цель лекции: Дать представление о достижимости и контрдостижимости и способах их нахождения
Достижимость и контрдостижимость
Задач, в которых используется понятие достижимости, довольно много. Вот одна из них. Граф может быть моделью какой-то организации, в которой люди представлены вершинами, а дуги интерпретируют каналы связи. При рассмотрении такой модели можно поставить вопрос, может ли информация от одного лица хi быть передана другому лицу хj, т. е. существует ли путь, идущий от вершины хi к вершине хj. Если такой путь существует, то говорят, что вершина хj достижима из вершины хi. Можно интересоваться достижимостью вершины хj из вершины хi только на таких путях, длины которых не превосходят заданной величины или длина которых меньше наибольшего числа вершин в графе и т. п. задачи.
Достижимость в графе описывается матрицей достижимости R=[rij], i, j=1, 2, … n, где n – число вершин графа, а каждый элемент определяется следующим образом:
rij=1, если вершина хj достижима из хi,
rij=0, в противном случае.
Множество вершин R(xi) графа G, достижимых из заданной вершины xi, состоит из таких элементов xj, для которых (i, j)-й элемент в матрице достижимостей равен 1. Очевидно, что все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима из себя самой путeм длины 0. Поскольку прямое отображение 1-го порядка Г+1(xi) является множеством таких вершин xj, которые достижимы из xi с использованием путей длины 1, то множество Г+(Г+1(xi)) = Г+2(xi) состоит из вершин, достижимых из xi с использованием путей длины 2. Аналогично Г+p(xi) является множеством вершин, которые достижимы из xi с помощью путей длины p.
Так как любая вершина графа, которая достижима из xi, должна быть достижима с использованием пути (или путей) длины 0 или 1, или 2, …, или p, то множество вершин, достижимых для вершины xi, можно представить в виде
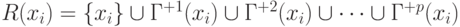
Как видим, множество достижимых вершин R(xi) представляет собой прямое транзитивное замыкание вершины xi, т. е. R (xi) = T+(xi). Следовательно, для построения матрицы достижимости находим достижимые множества R (xi) для всех вершин 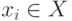
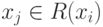
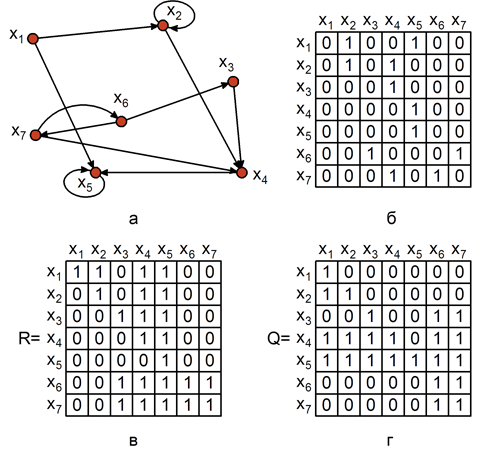
Рис.
4.1.
Достижимость в графе: а –граф; б – матрица смежности; в – матрица достижимости; г- матрица контрдостижимости.
Для графа, приведенного на
рис.
4.1,а, множества достижимостей находятся следующим образом:

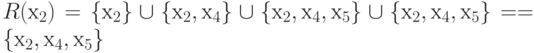

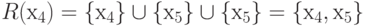
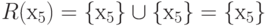
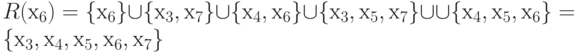
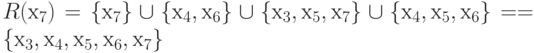
Матрица достижимости имеет вид, как показано на
рис.
4.1,в. Матрицу достижимости можно построить по матрице смежности (
рис.
4.1,б), формируя множества T+(xi) для каждой вершины xi
.
Матрица контрдостижимости Q = [ qij], i, j =1, 2, … n, где n – число вершин графа, определяется следующим образом:
qij=1, если из вершины xj
можно достичь вершину xi
,
qij=0, в противном случае.
Контрдостижимым множеством Q (xi) является множество таких вершин, что из любой вершины этого множества можно достичь вершину xi
. Аналогично построению достижимого мно-жества R (xi) можно записать выражение для Q (xi):
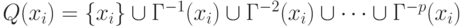
Таким образом, видно, что Q (xi) – это есть не что иное как обратное транзитивное замыкание вершины xi
, т. е. Q (xi) = Т—xi). Из определений очевидно, что столбец xi
матрицы Q (в котором qij=1, если 
матрицы R, т. е. Q = RT,где RT
– матрица, транспонированная к матрице достижимости R.
Матрица контрдостижимости показана на
рис.
4.1,г.
Следует отметить, что поскольку все элементы матриц R и Q равны 1 или 0, то каждую строку можно хранить в двоичной форме, экономя затраты памяти ЭВМ. Матрицы R и Q удобны для обработки на ЭВМ, так как с вычислительной точки зрения основными операциями являются быстродействующие логические операции.
Рассматриваются вопросы достижимости
для орграфов и способы нахождения матриц
достижимости и контрдостижимости.
Рассматривается матричный способ
нахождения количества путей между
любыми вершинами графа, а также нахождение
множества вершин, входящих в путь между
парой вершин. Цель лекции: Дать
представление о достижимости и
контрдостижимости и способах их
нахождения
Достижимость и
контрдостижимость
Задач, в которых используется понятие
достижимости, довольно много.
Вот одна из них. Графможет быть
моделью какой-то организации, в которой
люди представлены вершинами, а дуги
интерпретируют каналы связи. При
рассмотрении такой модели можно поставить
вопрос, может ли информация от одного
лицахiбыть передана другому лицухj, т. е. существует ли путь, идущий от
вершиныхiк вершинехj. Если такой путь существует, то говорят,
что вершинахjдостижимаиз вершиныхi.
Можно интересоваться достижимостью
вершиныхjиз вершиныхiтолько на таких путях, длины которых не
превосходят заданной величины или длина
которых меньше наибольшего числа вершин
в графе и т. п. задачи.
Достижимость в графе описывается
матрицей достижимости R=[rij],
i, j=1, 2, … n, гдеn–
число вершин графа, а каждый элемент
определяется следующим образом:
rij=1,
если вершинахjдостижима изхi,
rij=0,
в противном случае.
Множество вершин R(xi)графаG, достижимых из
заданной вершиныxi, состоит из таких элементовxi, для которых(i, j)-й
элемент в матрице достижимостей равен
1. Очевидно, что все диагональные элементы
в матрицеRравны 1,
поскольку каждая вершина достижима из
себя самой путeм длины 0. Поскольку прямое
отображение 1-го порядкаГ+1(xi)является множеством таких вершинxj, которые достижимы изxiс использованием путей длины 1, то
множествоГ+(Г+1(xi))
= Г+2(xi)состоит из вершин, достижимых изxiс использованием путей длины 2. АналогичноГ+p(xi)является множеством вершин, которые
достижимы из xi с помощью путей
длиныp.
Так как любая вершина графа, которая
достижима из xi, должна быть достижима с использованием
пути (или путей) длины 0 или 1, или 2, …,
илиp, то множество
вершин, достижимых для вершиныxi, можно представить в виде
R (xi)
= { xi }
Г+1(xi)
Г+2(xi)
…
Г+p(xi).
Как видим, множество достижимых вершин
R(xi)представляет собой прямое транзитивное
замыкание вершиныxi, т. е.R(xi)
= T+(xi).
Следовательно, для построения матрицы
достижимости находим достижимые
множестваR(xi)для всех вершинxiX.
Полагая,rij=1,
еслиxj
R(xi)иrij=0в противном случае.
Рис. 4.1. Достижимость в графе: а –граф;
б – матрица смежности; в – матрица
достижимости; г- матрица контрдостижимости.
Для графа, приведенного на рис. 4.1,а,
множества достижимостейнаходятся
следующим образом:
R (х1) = { х1}{ х2, х5}
{ х2, х4, х5 }
{ х2, х4, х5} = { х1,
х2, х4, х5},
R (х2) = { х2}{ х2, х4}
{ х2, х4, х5}
{
х2, х4, х5} = { х2,
х4, х5},
R (х3) = { х3}{ х4}
{ х5}
{ х5 } = { х3, х4, х5},
R (х4) = { х4}{ х5}
{ х5} = { х4, х5},
R (х5) = { х5}{ х5} = { х5},
R (х6) = { х6}{ х3, х7}
{ х4, х6}
{ х3, х5, х7}
{ х4, х5, х6} = { х3,
х4, х5, х6, х7},
R (х7) = { х7}{ х4, х6}
{ х3, х5, х7}
{ х4, х5, х6} = { х3,
х4, х5, х6, х7}.
Матрица достижимостиимеет вид,
как показано на рис. 4.1,в.Матрицу
достижимости можно построить поматрице смежности(рис. 4.1,б), формируя
множестваT+(xi)для каждой вершиныxi.
Матрица контрдостижимостиQ
= [ qij],i, j =1, 2, … n, гдеn– число вершин графа, определяется
следующим образом:
qij=1,
если из вершиныxjможно достичь вершинуxi,
qij=0,
в противном случае.
КонтрдостижимыммножествомQ
(xi)является множество таких вершин, что
из любой вершины этого множества можно
достичь вершинуxi. Аналогично построению достижимого
множестваR (xi)можно записать выражение дляQ
(xi):
Q (xi)
= { xi }
Г-1(xi)
Г—2(xi)
…
Г-p(xi).
Таким образом, видно, что Q
(xi)– это есть не что иное как обратное
транзитивное замыкание вершиныxi, т. е.Q (xi)
= Т—(xi).
Из определений очевидно, что столбец
xiматрицыQ(в
которомqij=1,
еслиxj
Q (xi),
иqij=0в противном случае) совпадает со строкойxi
матрицыR, т. е.Q
= RT,гдеRT– матрица, транспонированная кматрице
достижимостиR.
Матрица контрдостижимостипоказана
на рис. 4.1,г.
Следует отметить, что поскольку все
элементы матриц RиQравны 1 или 0, то каждую строку можно
хранить в двоичной форме, экономя затраты
памяти ЭВМ. МатрицыRиQудобны для обработки
на ЭВМ, так как с вычислительной точки
зрения основными операциями являются
быстродействующие логические операции.
Нахождение
множества вершин, входящих в путь
Если необходимо узнать о вершинах графа,
входящих в эти пути, то следует вспомнить
определения прямого и обратного
транзитивных замыканий. Так как T+(xi)– это множество вершин, в которые есть
пути из вершиныxi,
аT–(хj)– множество вершин, из которых есть
пути вxj, тоT+(xi)
T–(xj)– множество вершин, каждая из которых
принадлежит, по крайней мере, одному
пути, идущему отxiкxj
. Эти вершины называются существенными
или неотъемлемыми относительно двух
концевых вершинxiиxj. Все остальные вершины графа называются
несущественными или избыточными,
поскольку их удаление не влияет на пути
отxiкxj.
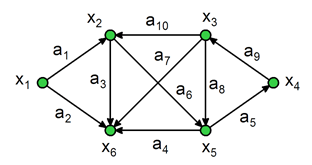
Рис. 4.2. Орграф
Так для графа на рис. 4.2 нахождение
вершин, входящих в путь, например из
вершины х2в вершинух4, сводится к нахождениюТ+(
х2)
={ х2,
х3,
х4,
х5,
х6},
Т—(
х4)
={ х1,
х2,
х3,
х4,
х5},
и их пересеченияT+(х2)
T–(х4)
={ х2,
х3,
х4,
х5}.
Матричный метод нахождения путей в
графах
Матрица смежности полностью определяет
структуру графа. Возведем матрицу
смежности в квадрат по правилам
математики. Каждый элемент матрицы А2
определяется по формуле
a(2)ik=nj=1aijajk
Слагаемое в формуле равно 1 тогда и
только тогда, когда оба числа aijиajk
равны 1, в противном случае оно равно
0. Поскольку из равенстваaij
= ajk
= 1следует существование пути длины
2 из вершиныxiв вершинухk, проходящего через вершинуxj, то (i -й,k-й) элемент матрицыА2равен числу путей длины 2, идущих изxiвхk.
В таблице 4.1a представлена матрица
смежности графа, изображенного на рис.
4.2. Результат возведения матрицы смежности
в квадрат А2показан в таблице 4.1б.
Так «1», стоящая на пересечении
второй строки и четвертого столбца,
говорит о существовании одного пути
длиной 2 из вершины х2к вершинех4. Действительно, как видим вграфена рис. 4.2, существует такой путь:a6,
a5. «2» в
матрицеA2говорит о существовании двух путей
длиной 2 от вершиных3к вершинех6:a8,
a4иa10,
a3.
Аналогично для матрицы смежности,
возведенной в третью степень A3
(таблица 4.1в),a (3)
ikравно числу
путей длиной 3, идущих отxiкхk. Из четвертой строки матрицыA3видно, что пути длиной 3 существуют: один
изх4вх4(a9,
a8,
a5),
один изх4в
х5(a9,
a10,
a6)и два пути изх4вх6(a9,
a10,
a3
и a9,
a8,
a4).
МатрицаA4показывает существование путей длиной
4 (таблица 4.1г).
Таким образом, если a р
ikявляется
элементом матрицыAр,тоa р
ikравно числу
путей (не обязательно орцепей или простых
орцепей) длиныр, идущих
отxiкхk.
Соседние файлы в папке МОТС
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Матрица достижимости простого ориентированного графа 

Содержание
- 1 Способы построения матрицы достижимости
- 1.1 Перемножение матриц
- 1.1.1 Случай нескольких путей
- 1.1.2 Пример
- 1.2 Алгоритм Уоршелла
- 1.1 Перемножение матриц
- 2 Связанные понятия
- 2.1 Матрица сильной связности
- 2.1.1 Построение матрицы сильной связности
- 2.1.2 Пример
- 2.2 Матрица связности графа
- 2.3 Матрица контрдостижимости
- 2.1 Матрица сильной связности
- 3 Примечания
Способы построения матрицы достижимости
Перемножение матриц
Пусть дан простой граф 




По определению, матрица композиции отношений 



После нахождения матриц 






Случай нескольких путей
Если булевы операции 



Пример
Граф
Рассмотрим простой связный ориентированный граф 
Он имеет матрицу смежности 

Найдём булевы степени этой матрицы 





Получим матрицу достижимости

Таким образом, из вершины 
При использовании же алгебраических операций получится матрица

Она показывает количество путей длины от 1 до 4 между вершинами орграфа.
Алгоритм Уоршелла
Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за 
Связанные понятия
Матрица сильной связности
Матрица сильной связности простого орграфа — бинарная матрица, содержащая информацию обо всех сильно связанных вершинах в орграфе. Матрица сильной связности симметрична. У сильно связного графа такая матрица заполнена единицами.
Построение матрицы сильной связности
Матрица сильной связности может быть построена из матрицы достижимости. Пусть 



Пример
Рассмотрим тот же граф, что и ранее.
Его матрица достижимости:

Из неё получаем матрицу сильной связности:

Вершины 3 и 4 сильно связаны друг с другом и сами с собой.
Матрица связности графа
Для обычного (не ориентированного) связного графа существует понятие матрицы связности, сходное с матрицей достижимости.
Матрица контрдостижимости
Матрица контрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования.
Примечания
Матрица достижимости простого ориентированного графа [math]displaystyle{ G=(V, A) }[/math] — бинарная матрица замыкания по транзитивности отношения [math]displaystyle{ A }[/math] (оно задаётся матрицей смежности графа). Таким образом, в матрице достижимости хранится информация о существовании путей между вершинами орграфа.
Способы построения матрицы достижимости
Перемножение матриц
Пусть дан простой граф [math]displaystyle{ G=(V, A) }[/math], матрица смежности которого есть [math]displaystyle{ mathbf A = (a_{ij})_{n times n} }[/math], где [math]displaystyle{ a_{ij} = 1 Leftrightarrow (i, j) in A }[/math]. Матрица смежности даёт информацию о всех путях длины 1 (то есть дугах) в орграфе. Для поиска путей длины 2 можно найти композицию отношения [math]displaystyle{ A }[/math] с самим собой:
[math]displaystyle{ Acirc A = bigl { (a, c): exists b in V: (a, b), (b, c) in A bigr } }[/math].
По определению, матрица композиции отношений [math]displaystyle{ A circ A }[/math] есть [math]displaystyle{ mathbf{A^2} = ({a^2}_{ij})_{n times n}=Bigl (sum_k a_{ik} a_{kj} Bigr )=Bigl ( (a_{i1} land a_{1j}) lor (a_{i2} land a_{2j} ) lor ldots lor (a_{in} land a_{nj}) Bigr ) }[/math], где [math]displaystyle{ land }[/math] — конъюнкция, а [math]displaystyle{ lor }[/math] — дизъюнкция.
После нахождения матриц [math]displaystyle{ mathbf A^k }[/math] композиций [math]displaystyle{ underbrace {A circ ldots circ A}_k }[/math] для всех [math]displaystyle{ k }[/math], [math]displaystyle{ 1 leq k leq n-1 }[/math] будет получена информация о всех путях длины от [math]displaystyle{ 1 }[/math] до [math]displaystyle{ n-1 }[/math]. Таким образом, матрица [math]displaystyle{ mathbf {R(G)} = mathbf E lor mathbf{A} lor mathbf{A^2} lor ldots lor mathbf{A^{n-1}} = ({a^*}_{ij})_{n times n} = ({a}_{ij} lor {a^2}_{ij} lor ldots lor {a^{n-1}}_{ij}) }[/math] есть искомая матрица достижимости, где [math]displaystyle{ mathbf E }[/math] — единичная матрица.
[math]displaystyle{
mathbf E =
begin{pmatrix}
1&0&0&0 \
0&1&0&0 \
0&0&1&0 \
0&0&0&1
end{pmatrix}
}[/math]
Случай нескольких путей
Если булевы операции [math]displaystyle{ lor, land }[/math] дизъюнкции и конъюнкции заменить обычными алгебраическими операциями [math]displaystyle{ +, times }[/math] сложения и умножения соответственно, нахождение матрицы достижимости [math]displaystyle{ mathbf{R(G)} }[/math] сведётся к обычному пошаговому перемножению матриц с последующим сложением результатов каждого шага. Тогда получившаяся матрица [math]displaystyle{ mathbf{R(G)} }[/math] будет состоять не только из 0 и 1 и будет характеризовать не только наличие путей между вершинами, но уже и количество таких путей. В таком случае можно разрешить наличие кратных рёбер в графе.
Пример
Граф [math]displaystyle{ G=(V, A) }[/math]
Рассмотрим простой связный ориентированный граф [math]displaystyle{ G=(V={1, 2, 3, 4}, A
={(1, 2), (1, 3), (3, 2), (3, 4), (4, 3)}) }[/math].
Он имеет матрицу смежности [math]displaystyle{ mathbf A }[/math] вида:
[math]displaystyle{
mathbf A =
begin{pmatrix}
0&1&1&0 \
0&0&0&0 \
0&1&0&1 \
0&0&1&0
end{pmatrix}
}[/math]
Найдём булевы степени этой матрицы [math]displaystyle{ mathbf{A^2} }[/math], [math]displaystyle{ mathbf{A^3} }[/math]:
[math]displaystyle{
mathbf{A^2} =
begin{pmatrix}
0&1&0&1 \
0&0&0&0 \
0&0&1&0 \
0&1&0&1
end{pmatrix}
}[/math],
[math]displaystyle{
mathbf{A^3} =
begin{pmatrix}
0&0&1&0 \
0&0&0&0 \
0&1&0&1 \
0&0&1&0
end{pmatrix}
}[/math],
Получим матрицу достижимости
[math]displaystyle{ mathbf{R(G)} = mathbf{E lor A lor A^2 lor A^3} = begin{pmatrix} 1&1&1&1 \ 0&1&0&0 \ 0&1&1&1 \ 0&1&1&1 end{pmatrix} }[/math]
Таким образом, из вершины [math]displaystyle{ 1 }[/math] можно добраться в любую другую.
При использовании же алгебраических операций получится матрица
[math]displaystyle{ mathbf{R(G)} = mathbf{E + A + A^2 + A^3} = begin{pmatrix} 1&2&2&1 \ 0&1&0&0 \ 0&2&2&2 \ 0&1&2&2 end{pmatrix} }[/math]
Она показывает количество путей длины от 0 до 3 между вершинами орграфа.
Алгоритм Уоршелла
Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за [math]displaystyle{ 2n^3 }[/math] шагов — алгоритм Уоршелла.
Связанные понятия
Матрица сильной связности
Матрица сильной связности простого орграфа — бинарная матрица, содержащая информацию обо всех сильно связанных вершинах в орграфе. Матрица сильной связности симметрична. У сильно связного графа такая матрица заполнена единицами.
Построение матрицы сильной связности
Матрица сильной связности может быть построена из матрицы достижимости. Пусть [math]displaystyle{ mathbf E^* }[/math] — матрица достижимости орграфа [math]displaystyle{ G=(V, E) }[/math]. Тогда матрица сильной связности [math]displaystyle{ mathbf C }[/math] состоит из элементов [math]displaystyle{ (c_{ij}) = left ( (e_{ij}) land (e_{ji}) right ) }[/math].
Пример
Рассмотрим тот же граф, что и ранее.
Его матрица достижимости:
[math]displaystyle{ mathbf{E^*} = begin{pmatrix} 1&1&1&1 \ 0&1&0&0 \ 0&1&1&1 \ 0&1&1&1 end{pmatrix} }[/math]
Из неё получаем матрицу сильной связности:
[math]displaystyle{ mathbf{C} = begin{pmatrix} 1&0&0&0 \ 0&1&0&0 \ 0&0&1&1 \ 0&0&1&1 end{pmatrix} }[/math]
Вершины 3 и 4 сильно связаны друг с другом и сами с собой.
Матрица связности графа
Для обычного (не ориентированного) связного графа существует понятие матрицы связности, сходное с матрицей достижимости.
|
|
Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
Матрица контрдостижимости
Матрица контрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования.