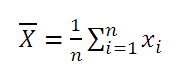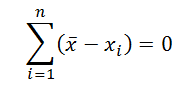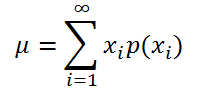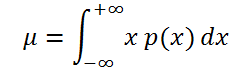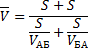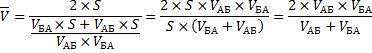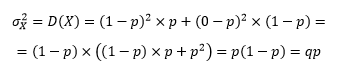Как найти мат ожидание в excel

Вычислим среднее значение выборки и математическое ожидание случайной величины в MS EXCEL.

Выборочное среднее

Среднее выборки

или

выборочное среднее

(sample average, mean) представляет собой

среднее

арифметическое

всех значений

выборки

.

В MS EXCEL для вычисления

среднего выборки

можно использовать функцию

СРЗНАЧ()

. В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения

выборки

.

Выборочное среднее

является «хорошей» (несмещенной и эффективной) точечной оценкой

математического ожидания

случайной величины (см.

ниже

), т.е.

среднего значения

исходного распределения, из которого взята

выборка

.

Примечание

: О вычислении

доверительных интервалов

при оценке

математического ожидания

можно прочитать, например, в статье

Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL

Некоторые свойства

среднего арифметического

:

Сумма всех отклонений от

среднего значения

равна 0:

Если к каждому из значений x
_i
прибавить одну и туже константу

с

, то

среднее арифметическое

увеличится на такую же константу;
Если каждое из значений x
_i
умножить на одну и туже константу

с

, то

среднее арифметическое

умножится на такую же константу.

Математическое ожидание

Среднее значение

можно вычислить не только для выборки, но для случайной величины, если известно ее

распределение

. В этом случае

среднее значение

имеет специальное название —

Математическое ожидание.

Математическое ожидание

характеризует «центральное» или среднее значение случайной величины.

Примечание

: В англоязычной литературе имеется множество терминов для обозначения

математического ожидания

: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет

дискретное распределение

, то

математическое ожидание

вычисляется по формуле:

где x
_i
– значение, которое может принимать случайная величина, а р(x
_i
) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет

непрерывное распределение

, то

математическое ожидание

вычисляется по формуле:

где р(x) –

плотность вероятности

(именно

плотность вероятности

, а не вероятность, как в дискретном случае).

статьи про распределения

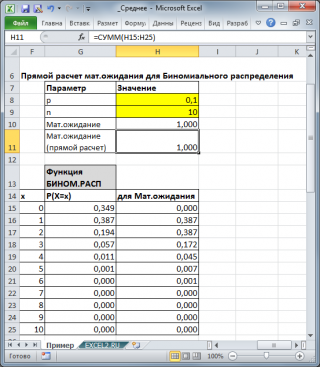
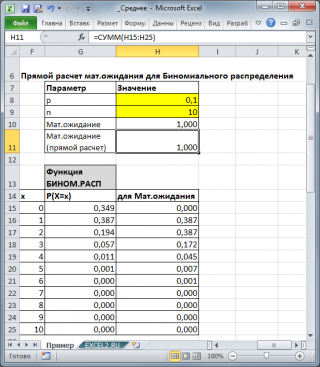
). Например, для

Биномиального распределения

среднее значение

равно произведению его параметров: n*p (см.

файл примера

).

Свойства математического ожидания

E[a*X]=a*E[X], где а — const

E[X+a]=E[X]+a

E[a]=a

E[E[X]]=E[X] — т.к. величина E[X] — является const

E[X+Y]=E[X]+E[Y] — работает даже для случайных величин не являющихся независимыми.

СОВЕТ

: Про другие показатели распределения —

Дисперсию

и

Стандартное отклонение,

можно прочитать в статье

Дисперсия и стандартное отклонение в MS EXCEL

Источник

Формула математическое ожидания в MS Excel – расчет по шагам

Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки.

В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки.

Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже), т.е. среднего значения исходного распределения, из которого взята выборка.

Примечание: О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL.

Некоторые свойства среднего арифметического:

Сумма всех отклонений от среднего значения равна 0:

Если к каждому из значений x_i прибавить одну и туже константу с, то среднее арифметическое увеличится на такую же константу;
Если каждое из значений x_i умножить на одну и туже константу с, то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:

где x_i – значение, которое может принимать случайная величина, а р(x_i) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:

где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).

Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

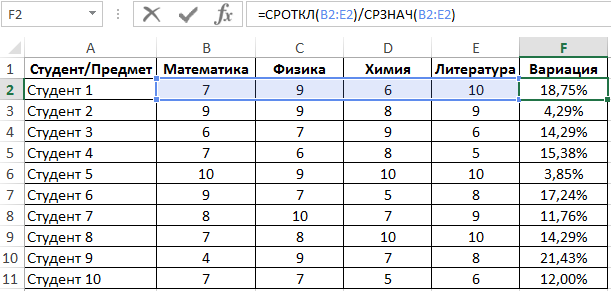
Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Примеры методов анализа числовых рядов в Excel

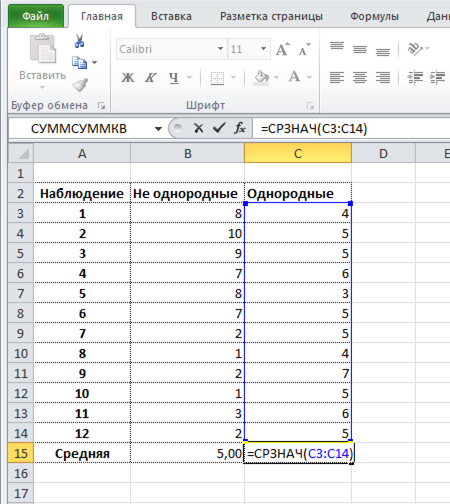
Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20).

Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.

Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.

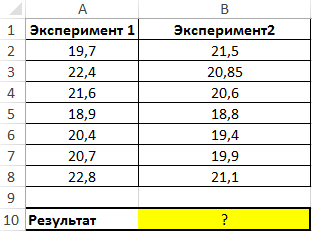
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?

Вид таблицы данных:

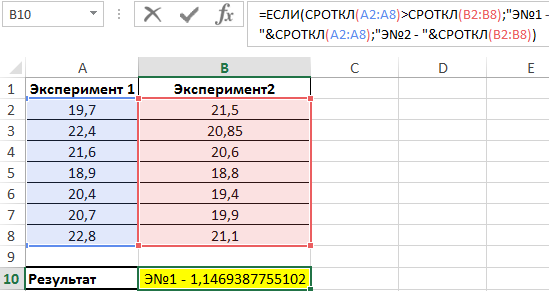
Используем следующую формулу:

Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.

В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.

Формула расчета линейного коэффициента вариации в Excel

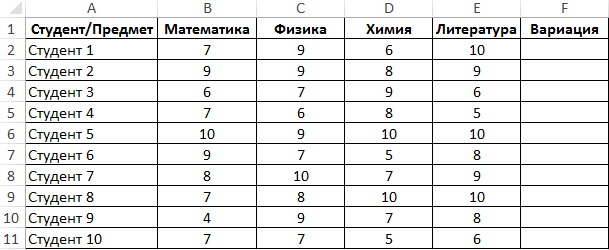
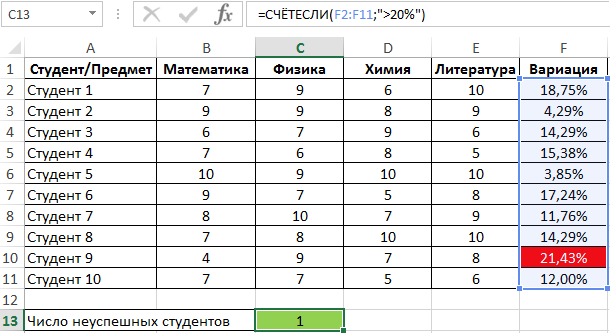
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.

Вид таблицы данных:

Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:

Растянем ее вниз по столбцу и получим следующие значения:

Для определения числа неуспешных студентов по указанному критерию используем функцию:

Правила использования функции СРОТКЛ в Excel

Функция имеет следующий синтаксис:

=СРОТКЛ( число1 ;[число2];. )

число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
[число2];… – необязательный, принимает второе и последующие значения из исследуемого числового ряда.

При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ(<2;5;4;7;10>).
Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.

1. Вычислить математическое ожидание:

1) Пуск > Все программы > Microsoft Office > Microsoft Excel

2) Так как функция математического ожидания это т оже самое, что и функция среднего арифметического, то: в пустой ячейке вводим «=», далее нажимаем fx, выбираем функцию СРЗНАЧ, выделяем числовые данные нашей исходной таблицы.

2. Вычислить дисперсию:

Вводим =, далее – fx, “Статистические” – “ДИСП”, выделить числовые данные нашей исходной таблицы.

3. Среднее квадратичесое отклонение (не смещённое):

Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.

4. Среднее квадратическое отклонение (смещённое):

Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.

Вывод: Microsoft Excel является одной из самых удобных компьютерных программ, с помощью которых можно высчитать статические данные. В этом я убедился, когда высчитывал вышеуказанные данные.

Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки .

В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки .

Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже ), т.е. среднего значения исходного распределения, из которого взята выборка .

Примечание : О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL .

Некоторые свойства среднего арифметического :

Сумма всех отклонений от среднего значения равна 0:

Если к каждому из значений x _i прибавить одну и туже константу с , то среднее арифметическое увеличится на такую же константу;
Если каждое из значений x _i умножить на одну и туже константу с , то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение . В этом случае среднее значение имеет специальное название — Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание : В англоязычной литературе имеется множество терминов для обозначения математического ожидания : expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет дискретное распределение , то математическое ожидание вычисляется по формуле:

где x _i – значение, которое может принимать случайная величина, а р(x _i ) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение , то математическое ожидание вычисляется по формуле:

где р(x) – плотность вероятности (именно плотность вероятности , а не вероятность, как в дискретном случае).

Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения ). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

Свойства математического ожидания

E[a*X]=a*E[X], где а — const

E[E[X]]=E[X] — т.к. величина E[X] — является const

E[X+Y]=E[X]+E[Y] — работает даже для случайных величин не являющихся независимыми.

СОВЕТ : Про другие показатели распределения — Дисперсию и Стандартное отклонение, можно прочитать в статье Дисперсия и стандартное отклонение в MS EXCEL .

Среднее арифметическое в Excel

Среднее арифметическое значение — самый известный статистический показатель. В этой заметке рассмотрим его смысл, формулы расчета и свойства.

Средняя арифметическая как оценка математического ожидания

Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.

Формула матожидания имеет следующий вид:

где M(X) – математическое ожидание

x_i – это случайные величины

То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.

Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.

Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.

Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.

где x_i – значения переменной,
n – количество значений.

Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).

Свойства средней арифметической (математического ожидания)

Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.

Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).

Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.

M(X+Y+Z) = M(X) + M(Y) + M(Z)

Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.

Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.

К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.

Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).

Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.

Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.

Формула среднего значения в Excel

Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.

У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.

Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:

После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.

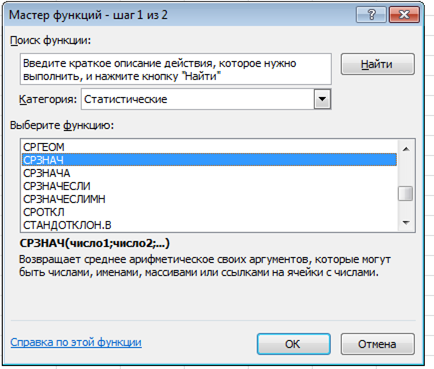
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).

Средняя арифметическая взвешенная

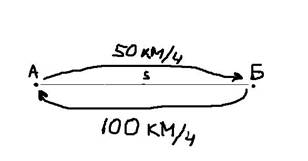
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.

Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.

Формула средневзвешенного значение в Excel

Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.

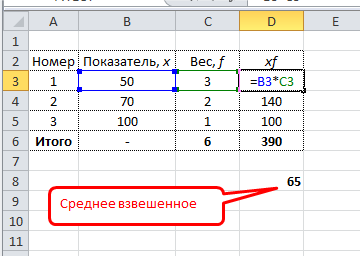
Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.

Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:

Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.

Физический смысл средней арифметической

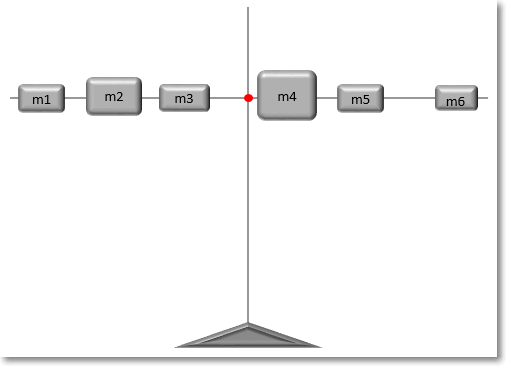
Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.

Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (m_i), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.

И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.

Источник

1.
Выборочная оценка математического
ожидания – выборочное среднеев Excel
вычисляется с помощью
функция СРЗНАЧ,
при этом
реализуется формула
.

2.
Оценка дисперсии – несмещенная
(исправленная) выборочная дисперсияможет быть получена с помощью функцииДИСП.
В Excel
реализована формула
.

3.
Несмещенное выборочное средние
квадратические отклонения (стандартное
отклонение)
вычисляется
с помощью функции
СТАНДОТКЛОН.
Вычисления
в Excel
выполнены по формуле

4.
Выборочная (смещенная) оценка дисперсии

вычисляется с помощью
функция ДИСПР.

Результат
вычисления выборочных оценок
,

,
и
показан на рис.1.

… … … …
… … …

Рис.
1. Фрагмент листа Excel
с исходными данными и выборочными
оценками параметров.

2. Описательная статистика.

Выполните
процедуру Описательная
статистика.

В
главном меню Excel
выбрать: Данные
→ Анализ данных → Описательная статистика
→ ОК.

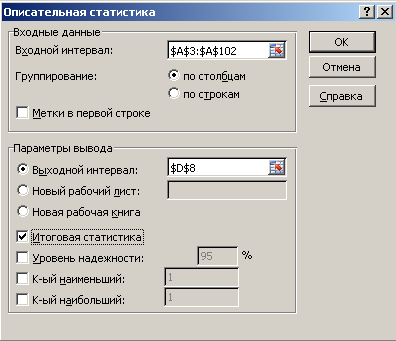
В
появившемся окне Описательная
статистика
ввести:

Входной
интервал –
100 случайных чисел в ячейках $A$3:
$A$102;

Группирование
— по столбцам;

Выходной
интервал –
адрес ячейки, с которой начинается
таблица Описательная
статистика – например,
$D$8;

Итоговая
статистика
– поставить галочку. ОК.

Рис.
2. Диалоговое окно Описательная
статистика
с заполненными полями ввода.

На
листе Excel
появится таблица – Столбец
1. В
таблице даются все необходимые параметры,
кроме моды Mo(X).

Рис.
3. Таблица Описательная
статистика

Таблица содержит
описательные статистики, в частности:

Среднее
– оценка математического ожидания
;

Стандартное
отклонение
– оценка среднего квадратического
отклонения;

Дисперсия
– выборочная исправленная дисперсия
;

Эксцесс
и Асимметричность
– оценки эксцесса и асимметрии;

Медиана
– оценка
медианы;

Мода
– оценка
моды, #Н/Д – нет данных (наиболее часто
встречающееся значение случайной
величины в выборке).

Приблизительное
равенство нулю оценок эксцесса и
асимметрии, и приблизительное равенство
оценки среднего оценке медианы дает
предварительное основание выбрать в
качестве основной гипотезы H₀
распределения элементов генеральной
совокупности — нормальный закон.

Интервал
– размах выборки;

Минимум
– минимальное значение случайной
величины в выборке ;

Максимум
– максимальное значение случайной
величины в выборке .

Результаты
процедуры Описательная
статистика
потребуются в дальнейшем при построении
теоретического закона распределения.

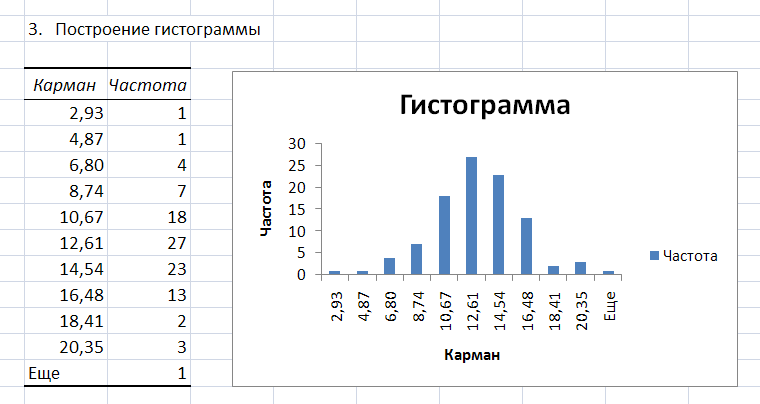
3. Построение гистограммы

В
главном меню Excel
выбрать Данные
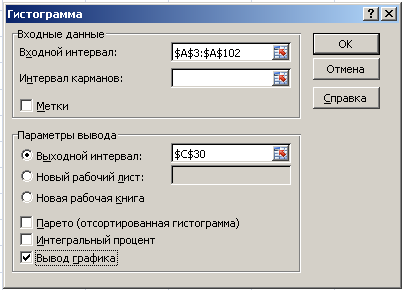
→ Анализ данных → Гистограмма → ОК.

Далее
необходимо заполнить поля ввода в
диалоговом окне Гистограмма.

Входной
интервал:
100 случайных чисел в ячейках $A$3:
$A$102;

Интервал
карманов:
не
заполнять;

Выходной
интервал:
адрес ячейки, с которой начинается вывод
результатов процедуры Гистограмма;

Вывод
графика –
поставьте галочку.

Если
поле ввода Интервал
карманов не
заполняется, то процедура вычисляет
число интервалов группировки k
и границы интервалов автоматически по
формуле.

где,
скобки
означают – округление до целой части
числа в меньшую сторону.

В
рассматриваемом варианте n
= 100,
следовательно, k
= 11.
Действительно:

Рис.
4. Диалоговое окно Гистограмма.

В
результате выполнения процедуры
Гистограмма
появляется таблица, содержащая границы
x_i
интервалов
группировки (столбец – Карман)
и частоту попадания случайных величин
выборки m_i
в i–ый
интервал (столбец
–
Частота).

Справа от таблицы
– график гистограммы.

Рис.
5. Фрагмент листа Excel
с результатами процедуры Гистограмма.

По
виду гистограммы можно предположить
(принять гипотезу) о том, что выборка
случайных чисел подчиняется нормальному
закону распределения.

Далее,
для того чтобы убедиться в правильности
выбранной гипотезы (по крайней мере
визуально) надо, первое – построить
график гипотетического нормального
закона распределения, выбрав в качестве
параметров (математического ожидания
и среднего квадратического отклонении)
их оценки (среднее и стандартное
отклонение), и совместить график
гипотетического распределения с графиком
гистограммы.

И,
второе – используя критерий согласия
Пирсона установить справедливость
выбранной гипотезы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает. Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом».

Эксперименты с такими данными называются схемой Бернулли, в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.

Переменная альтернативного признака

Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.

Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.

Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5. Такая вероятность традиционно обозначается латинской буквой p. Следовательно, вероятность наступления альтернативного события равна 1 — p, которую еще обозначают через q, то есть q = 1 – p. Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X.

Мы получили перечень возможных значений и их вероятности. Можно рассчитать математическое ожидание и дисперсию. Матожидание – это сумма произведений всех возможных значений на соответствующие им вероятности:

Вычислим матожидание, используя обозначения в таблицы выше.

Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p.

Теперь определим, что такое дисперсия альтернативного признака. Дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:

Отсюда дисперсия альтернативного признака:

Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5).

Стандартное отклонение – корень из дисперсии:

Максимальное значение не превышает 0,5.

Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.

Биномиальное распределение случайной величины

Рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве бросков.

Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X, т.е. количеству единичных исходов.

Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 – все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.

Матожидание биномиальной переменной получить очень легко. Математическое ожидание суммы величин есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:

Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.

Теперь выведем формулу дисперсии биномиальной переменной. Дисперсия суммы независимых случайных величин есть сумма дисперсий. Отсюда

Стандартное отклонение, соответственно

Для 100 подбрасываний монеты стандартное отклонение количества орлов равно

И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k, где 0≤ k ≤n. Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?

Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга. Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка. Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:

Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке. Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Всего 6 вариантов.

Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.

Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно. Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k, где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:

Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).

Формулу для определения вероятности легко обобщить на любое количество n и k. В итоге формула биномиального распределения имеет следующий вид.

Количество подходящих под условие комбинаций умножить на вероятность одной из них.

Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.

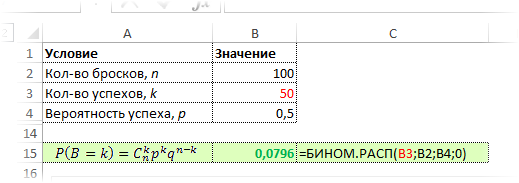
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:

Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.

Расчет вероятностей биномиального распределения в Excel

Если использовать только бумагу и калькулятор, то расчеты по формуле биномиального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков. Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.

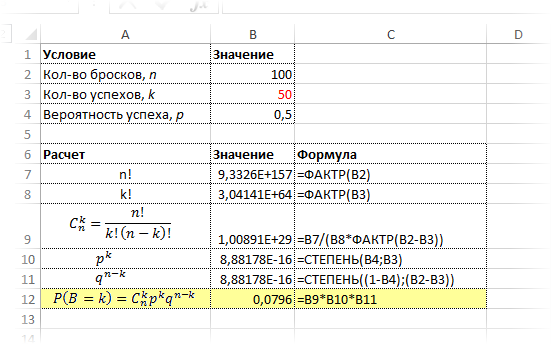
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.

Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.

В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.

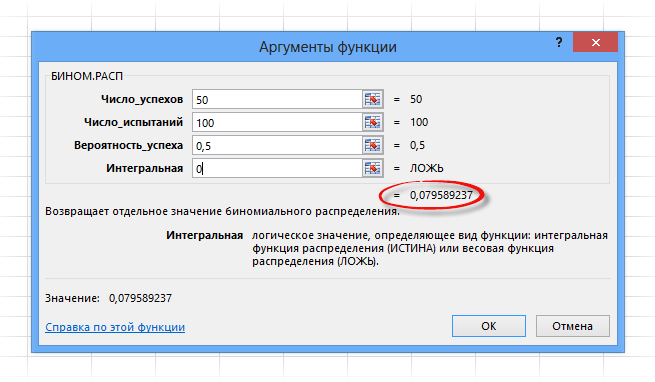
Синтаксис функции состоит из 4 аргументов:

Поля имеют следующие назначения:

Число успехов – количество успешных испытаний. У нас их 50.

Число испытаний – количество бросков: 100 раз.

Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.

Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k); если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.

Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.

Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.

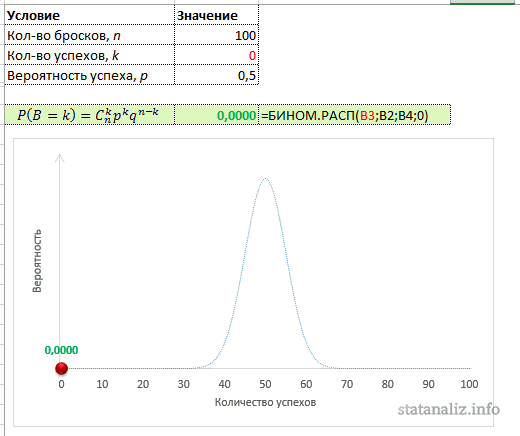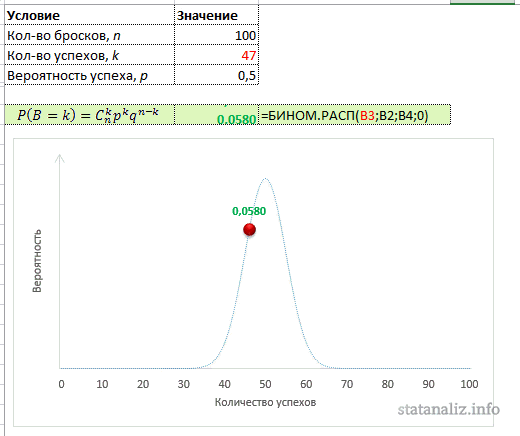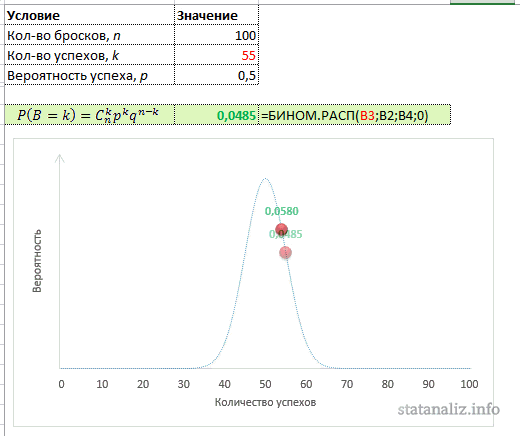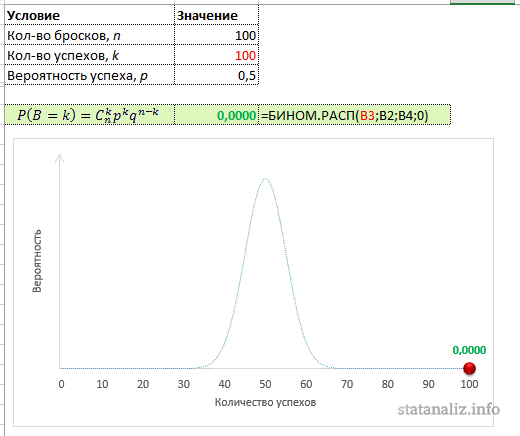
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100. То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в следующей картинке. Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.

Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.

Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро.

Поделиться в социальных сетях:

Источник

Математическое ожидание – это среднее значение случайной величины.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

Пример. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:

Решение : Математическое ожидание равно сумме произведений всех возможных значений X на их вероятности:

Для вычисления математического ожидания удобно расчеты проводить в Excel (в особенности когда данных много), предлагаем воспользоваться готовым шаблоном ( калькулятор для вычисления математического ожидания ).

Пример для самостоятельного решения (можете применить калькулятор).
Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:

Математическое ожидание обладает следующими свойствами.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х).

Свойство 3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М (Х1Х2 . Хп)=М (X1) М <Х2)*. ..*М (Xn)

Свойство 4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Хг + Х2+. +Хn) = М<Хг)+М(Х2)+…+М(Хn).

Задача 189. Найти математическое ожидание случайной вели чины Z, если известны математические ожидания X н Y: Z = X+2Y, M(X) = 5, M(Y) = 3;

Решение : Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания), получим M(Z)=M(X + 2Y)=M(X) + M(2Y)=M(X) + 2M(Y)= 5 + 2*3 = 11.

190. Используя свойства мaтематического ожидания, доказать, что: а) М(Х — Y) = M(X)—М (Y); б) математическое ожидание отклонения X—M(Х) равно нулю.

191. Дискретная случайная величина X принимает три возможных значения: x1= 4 С вероятностью р1 = 0,5; xЗ = 6 С вероятностью P2 = 0,3 и x3 с вероятностью р3. Найти: x3 и р3, зная, что М(Х)=8.

192. Дан перечень возможных значений дискретной случайной величины X: x1 = —1, х2 = 0, x3= 1 также известны математические ожидания этой величины и ее квадрата: M(Х) = 0,1, М(Х^2)=0,9. Найти вероятности p1, p2,p3 соответствующие возможным значениям xi

194. В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание дискретной случайной величины X — числа нестандартных деталей среди двух отобранных.

196. Найти математическое ожидание дискретной случайной величины X—числа таких бросаний пяти игральных костей, в каждом из которых на двух костях по явится по одному очку, если общее число бросаний равно двадцати.

Математическое ожидание биномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании:

Пример. Устройство состоит из n элементов. Вероятность отказа любого элемента за время опыта равна р. Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно m элементов, если всего про изведено N опытов. Предполагается, что опыты независимы один от другого.

207. Найти математическое ожидание дискретной случайной величины X, распределенной по закону Пуассона:

Чтобы вычислить максимум, выделяете весь диапазон необходимых чисел в таблице и отдельную ячейку, затем кликаете по значку «Σ» или «Автосумма». В выпавшем окне выбираете «Максимум» и, нажав кнопку «Enter» получаете нужное значение.

Формирование инвестиционного портфеля Марковица в Excel

Первым шагом при вычислении дисперсии является определение среднего значения выборки, которое в нашем примере равняется 7,8 раза в месяц. Остальные вычисления можно облегчить с помощью следующей таблицы.

Использование метода «сырого счета» (пример с готовкой)

Существует более эффективный способ вычисления дисперсии, известный как метод «сырого счета». Хотя с первого взгляда уравнение может показаться весьма громоздким, на самом деле оно не такое уж страшное. Можете в этом удостовериться, а потом и решите, какой метод вам больше нравится.

— сумма каждого значения данных после возведения в квадрат,

Не теряйте рассудок прямо сейчас. Позвольте представить все это в виде таблицы, и тогда вы увидите, что вычислений здесь меньше, чем в предыдущем примере.

Как видите, результат получился тот же, что и при использовании предыдущего метода. Достоинства данного метода становятся очевидными по мере роста размера выборки (n).

Математическое ожидание — Студопедия

Выделяем ячейку и таким же способом, как и в предыдущий раз, запускаем Мастер функций.
В категории «Полный алфавитный перечень» или «Статистические» ищем наименование «ДИСП.В». После того, как формула найдена, выделяем её и делаем клик по кнопке «OK».
Производится запуск окна аргументов функции. Далее поступаем полностью аналогичным образом, как и при использовании предыдущего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Затем щелкаем по кнопке «OK».
Результат вычисления будет выведен в отдельную ячейку.

Чтобы произвести расчет, под числами, которые необходимо посчитать, выделяется ячейка. Заходите во вкладку вставки функции. Выбираете категорию «Статистические». В выпавшем списке выбираете одну из функций и кликаете по кнопке «Enter».

Цели формирования инвестиционного портфеля

Выделяют две инвестиционные стратегии при формировании портфеля:

► Максимизации доходности инвестиционного портфеля при ограниченном уровне риск.

► Минимизация риска инвестиционного портфеля при минимально допустимом уровне доходности.

Математическое ожидание — что это, формулы, как его найти, примеры и свойства — Узнай Что Такое

Данная модель была разработана для эффективных рынков капитала, на которых наблюдается постоянный рост стоимости активов и отсутствуют резкие колебания курсов, что было в большей степени характерно для экономики развитых стран 50-80-х годов. Корреляция между акциями не постоянна и меняется со временем, в итоге в будущем это не уменьшает систематический риск инвестиционного портфеля.
Будущая доходность финансовых инструментов (акций) определяется как среднеарифметическое. Данный прогноз основывается только на историческом значении доходностей акции и не включает влияние макроэкономических (уровень ВВП, инфляции, безработицы, отраслевые индексы цен на сырье и материалы и т.д.) и микроэкономических факторов (ликвидность, рентабельность, финансовая устойчивость, деловая активность компании).
Риск финансового инструмента оценивается с помощью меры изменчивости доходности относительно среднеарифметического, но изменение доходности выше не является риском, а представляет собой сверхдоходность акции.

Инвестиционный портфель – это совокупность различных финансовых инструментов, удовлетворяющих цели инвестора и, как правило, заключается в создании таких комбинаций активов, которые бы обеспечили максимальную доходность при минимальном уровне риска.

Как найти математическое ожидание в Excel?

В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки . Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см.

Как найти математическое ожидание пример?

Формула среднего случайной величины Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений xi , которые принимает СВ Х, на соответствующие вероятности pi: M(X)=n∑i=1xi⋅pi.

Как найти математическое ожидание?

Чтобы найти математическое ожидание случайной величины, следует вычислить сумму парных произведений всех возможных значений случайной величины на соответствующие им вероятности.

Как найти мат ожидание произведения?

Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин. М(XY) = M(X) × M(Y). Постоянный множитель можно выносить за знак математического ожидания: M(C×X)=C×M(X).

Как рассчитать дисперсию в Excel?

Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q. Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x).

Как вычислить среднюю арифметическую в Эксель?

Расчет среднего значения чисел в подрядной строке или столбце

Щелкните ячейку снизу или справа от чисел, для которых необходимо найти среднее.
На вкладке «Главная» в группе «Редактирование» щелкните стрелку рядом с кнопкой » «, выберите «Среднее» и нажмите клавишу ВВОД.

Чему равна ковариация?

2. Ковариация от алгебраической суммы равна алгебраической сумме математических ожиданий от слагаемых, как по первому, так и по второму операнду. Доказательство следует из свойств математического ожидания.

Что такое математическое ожидание простыми словами?

Математическое ожидание – это число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание – это в теории вероятности средневзвешенная величина всех возможных значений, которые может принимать эта случайная величина.

Как посчитать математическое ожидание и дисперсию?

Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. Дисперсию находим по формуле d = ∑x2ipi — M[x]2.

Чему равно математическое ожидание?

Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора. Для случайной величины, принимающей значения только 0 или 1 математическое ожидание равно p — вероятности «единицы».

Как правильно считать дисперсию?

Дисперсия — это мера рассеяния, описывающая сравнительное отклонение между значениями данных и средней величиной. Является наиболее используемой мерой рассеяния в статистике, вычисляемая путем суммирования, возведенного в квадрат, отклонения каждого значения данных от средней величины.

Как подсчитать дисперсию?

Дисперсия случайной величины Х вычисляется по следующей формуле: D(X)=M(X−M(X))2, которую также часто записывают в более удобном для расчетов виде: D(X)=M(X2)−(M(X))2. Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.

Какая функция в формуле вычисляет среднее арифметическое значение из выбранного диапазона?

Примечание: Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении.

Как найти максимальное и минимальное значение в Excel?

В Excel формула = МАКС (диапазон) or = МИН (диапазон) может помочь вам получить максимальное или минимальное значение в диапазоне. Примечание: Чтобы рассчитать минимальные значения для каждого дня, примените эту формулу = МИН (B2: B5) в ячейке B6 и перетащите его маркер заполнения вправо в нужные ячейки.

Что такое ковариация простыми словами?

Ковариация простыми словами Ковариация — это мера того, как две случайные величины изменятся при сравнении друг с другом. Однако в финансовом или инвестиционном контексте термин ковариация описывает доходность двух разных инвестиций за период времени по сравнению с разными переменными.

Когда ковариация равна нулю?

Величина равняется нулю, если случайные величины и независимы (свойство (E7) математического ожидания).

В чем смысл математического ожидания?

Математическое ожидание – это сумма произведений всех возможных значений случайной величины на вероятности этих значений. Математическое ожидание – это средняя выгода от того или иного решения при условии, что подобное решение может быть рассмотрено в рамках теории больших чисел и длительной дистанции.

Прошу помочь студенту-первокурснику — необходимо найти (оценить с помощью приближенного интегрирования) математическое ожидание и дисперсию, найти точку максимума (моду) распределения в данной задаче (и, конечно, понять, как это делать в аналогичных задачах):

Построить на отрезке [0 ; 3] с шагом 0,1 график функции плотности вероятности Фишера со степенями свободы k₁=5 и k₂=9

Составить график не вызывает трудностей, однако я не могу разобраться, как найти ожидание, дисперсию и моду? Возможно, если мода — точка максимума, то ее находят просто путем нахождения точки максимума на графике через функцию «поиск решения»? Насчет ожидания и дисперсии: возможно, есть связь с оценкой по формуле правых/левых треугольников или трапеций? Но тогда как их здесь использовать? И какую именно формулу? Лишь формулу трапеций, для более точного результата?
Прилагаю составленный график.

Метод оценки риска VAR

Откройте счёт с тарифом «Всё включено» за 5 минут, не посещая офис.

проект «Открытие Инвестиции»

Открыть брокерский счёт

Тренировка на учебном счёте

Об «Открытие Инвестиции»

Москва, ул. Летниковская,
д. 2, стр. 4

8 800 500 99 66

Согласие на обработку персональных данных

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 г. (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Источник

Выборочное среднее

Математическое ожидание

Свойства математического ожидания

Формула математическое ожидания в MS Excel – расчет по шагам

Математическое ожидание

Примеры методов анализа числовых рядов в Excel

Формула расчета линейного коэффициента вариации в Excel

Математическое ожидание

Свойства математического ожидания

Среднее арифметическое в Excel

Средняя арифметическая как оценка математического ожидания

Свойства средней арифметической (математического ожидания)

Формула среднего значения в Excel

Средняя арифметическая взвешенная

Формула средневзвешенного значение в Excel

Физический смысл средней арифметической

2. Описательная статистика.

3. Построение гистограммы

Переменная альтернативного признака

Биномиальное распределение случайной величины

Расчет вероятностей биномиального распределения в Excel

Формирование инвестиционного портфеля Марковица в Excel

Использование метода «сырого счета» (пример с готовкой)

Математическое ожидание — Студопедия

Цели формирования инвестиционного портфеля

Математическое ожидание — что это, формулы, как его найти, примеры и свойства — Узнай Что Такое

Как найти математическое ожидание в Excel?

Как найти математическое ожидание пример?

Как найти математическое ожидание?

Как найти мат ожидание произведения?

Как рассчитать дисперсию в Excel?

Как вычислить среднюю арифметическую в Эксель?

Чему равна ковариация?

Что такое математическое ожидание простыми словами?

Как посчитать математическое ожидание и дисперсию?

Чему равно математическое ожидание?

Как правильно считать дисперсию?

Как подсчитать дисперсию?

Какая функция в формуле вычисляет среднее арифметическое значение из выбранного диапазона?

Как найти максимальное и минимальное значение в Excel?

Что такое ковариация простыми словами?

Когда ковариация равна нулю?

В чем смысл математического ожидания?

Как найти мат ожидание в excel

Метод оценки риска VAR

Не пропустите также: