Как найти массу тела при равноускоренном движении - Avtoru.top

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

Взаимосвязь скорости, времени и расстояния:
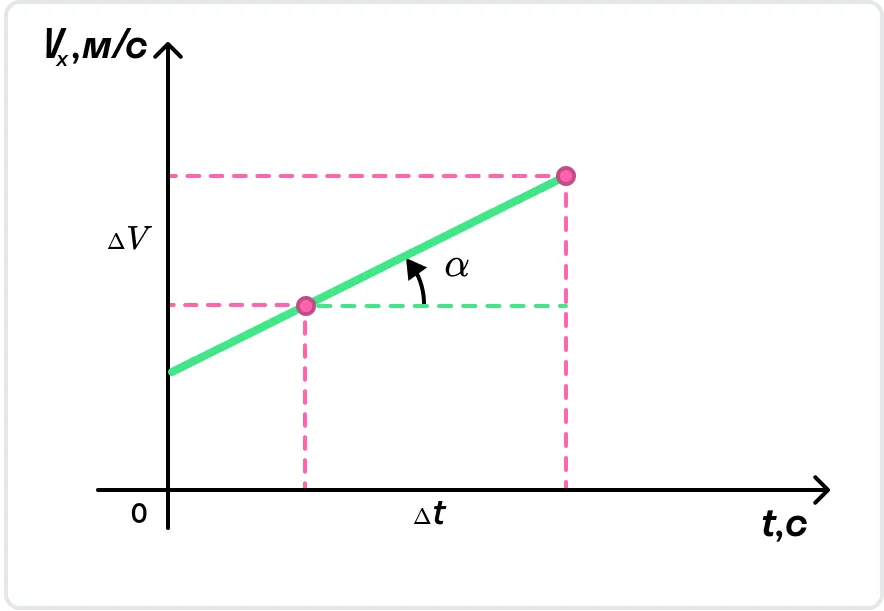
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

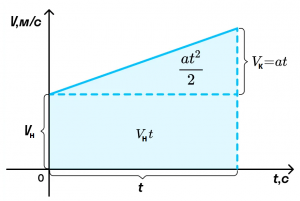
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:

Конвертер единиц измерения расстояния (длины)
Конвертер единиц измерения скорости
Конвертер единиц измерения времени

Источник

Содержание:

Масса
Второй закон Ньютона
Масса — мера инертности тела
Система единиц измерения механических величин
Примеры решения задач на второй закон Ньютона

Масса — это физическая величина, одна из основных характеристик материи, определяющая её инертные и гравитационные свойства, масса рассматривается как мера инертности тела по отношению к действующей на него силе и как источник поля тяготения равны (принцип эквивалентности), в международной системе единиц (си) обозначается в килограммах.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Масса

Всякое тело притягивается Землёй. Сила, с которой Земля притягивает тело, называется весом тела. С понятием веса тела тесно связано другое, более общее
понятие — масса тела.

Массой тела называется количество вещества, содержащегося в этом теле.

Масса литра воды в 1000 раз больше массы 1 см3 воды, масса бревна во много раз больше массы полена из такого же дерева. Словом, массы однородных тел тем больше, чем больше объёмы этих тел. При равенстве их объёмов равны и массы. Так, например, массы двух одинакового объёма кусков железа равны между собой. Если положить эти куски на чашки весов, то они окажутся в равновесии. Это даёт нам возможность измерять массы тел взвешиванием.

Рис. 98. Измерение массы тела.

Массы двух тел равны, если эти тела одинаково притягиваются Землёй в одном и том же месте,
т. е. если они уравновешивают друг друга на чашках рычажных весов. При этом совершенно безразлично, из каких веществ состоят эти тела. Если массу одного из этих тел принять за единицу массы, то и масса другого тела, которое уравновешивается первым, будет также равна единице массы.

За единицу массы принята масса платинового цилиндра, хранящегося в Сере (близ Парижа). Эта масса называется килограммом. В отличие от единицы силы, обозначаемой кГ, единица массы сокращённо обозначается кг.

В физике за единицу массы принимают 0,001 кг. Эта единица называется граммом (сокращённое обозначение—г).

В практике эталоны масс изготовляют в виде гирь различной величины.

Чтобы измерить массу тела, надо положить на одну чашку весов это тело, а на другую—гири. При равновесии весов масса тела равна массе гир,,. На рисунке 98 показано, что масса тела равна 0,5 кг.

Второй закон Ньютона

Во втором законе Ньютона устанавливается связь между силой, действующей на тело, массой тела и ускорением, с которым движется это тело.

Рис. 99. Прибор для установления зависимости ускорения от силы, действующей на тело.

Рассмотрим сначала, как зависит ускорение одного и того же тела от величины силы, действующей на тело. Проделаем следующий опыт (рис. 99). К тележке, которая может (с малым трением) двигаться по столу, прикреплён динамометр. К другому концу динамометра прикреплена нитка с грузом М, переброшенная через блок. По показаниям динамометра мы сможем определить силу, действующую на тележку. Пользуясь капельницей, отметим пути, пройденные тележкой при ускоренном движении за различные промежутки времени под действием постоянной силы. Измерения показывают, что пути эти пропорциональны квадратам времён. Таким образом, движение под действием постоянной силы есть равноускоренное движение.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле определяем ускорение а.

Будем подвешивать к концам нити различные грузы, каждый раз измеряя динамометром силу и вычисляя соответствующее этой силе ускорение тележки.

Результаты таких измерений и вычислений отражены в таблице.

Из таблицы видно, что с увеличением силы в 1,5 раза ускорение увеличивается тоже в 1,5 раза; если сила увеличивается в 2 раза, в 2 раза увеличивается и ускорение, и т. д., т. е. ускорение тележки прямо пропорционально силе, действующей на тележку.

Математически это можно записать в виде формулы:

Чтобы установить, как зависит ускорение от массы тела, будем действовать на тележку какой-нибудь постоянной силой.

Нагружая тележку гирями, изменим массу движущихся тел.

Ускорение, получаемое тележкой, будем вычислять так же, как и в первом случае.

Результаты опытов снова занесём в таблицу.

Данные таблицы показывают, что при неизменной силе увеличение массы тела в два раза приводит к уменьшению ускорения в два раза, и наоборот, при уменьшении массы в два раза ускорение увеличивается в два раза, т. е. ускорение тележки с грузами обратно пропорционально их общей массе. Математически этот вывод можно
выразить формулой:

Итак, результаты опытов показывают, что ускорение, с которым движется тело, пропорционально действующей на тело силе и обратно пропорционально массе этого тела.

Кроме того, ускорение тела совпадает с этой силой по направлению.

Этот вывод, как показал Ньютон, имеет всеобщий характер; он носит название второго закона Ньютона.

Во втором законе Ньютона говорится о действии одной силы. Но практически на тело всегда действуют несколько сил. Нам уже известно, что в расчётных целях мы действие нескольких сил можем заменить действием одной силы — равнодействующей. Поэтому в случае, когда на тело действуют несколько сил, под силой, вызывающей ускорение тела, подразумевается их равнодействующая.

Второй закон Ньютона математически можно выразить в виде следующей формулы:

откуда

Величина силы равна произведению массы тела на ускорение.

Таким образом, второй закон Ньютона позволяет вычислить величину силы, если известна масса тела и ускорение, с которым оно движется.

В частности, на основании второго закона Ньютона вес тела Р можно выразить через массу этого тела т и ускорение свободного падения g:

Р = mg.

Из сопоставления формулы F=ma и P=mg видно, что

т. е. ускорение движения тела под действием некоторой силы во столько же раз больше или меньше ускорения свободного падения, во сколько раз действующая сила больше или меньше веса тела.

При решении задач с помощью указанного выше отношения однородные величины должны быть выражены в одних и тех же единицах.

Пример. Санки с седоком весят 70 кГ и скатываются с горы с ускорением Определить силу, движущую санки.

Р=70 кГ;

g=
а =
F = ?

Из формулы определим F:

Масса — мера инертности тела

Первый закон Ньютона утверждает, что всякое тело обладает свойством инерции, иначе говоря, всякое тело инертно. Какова мера инертности тела? Обратимся к следующему примеру.

Пусть по горизонтальному пути с одинаковой скоростью движутся два вагона, один пустой, другой гружёный. Пусть на каждый из них одновременно начали действовать одинаковые силы, тормозящие их движение. Какой из этих вагонов будет дольше сохранять своё движение? Опыт показывает, что гружёный вагон будет двигаться дольше, следовательно, можно сказать, что он обладает и большей инертностью. Но масса гружёного вагона больше массы пустого; отсюда следует, что чем больше масса тела, тем более оно инертно.

Рис. 100. Масса наковальни значительно больше массы молота.

Этот вывод непосредственно вытекает из второго закона Ньютона. Действительно, по второму закону Ньютона т. е. ускорение обратно пропорционально массе, а так как масса гружёного вагона больше массы пустого, то и ускорение его движения будет меньше (ускорение направлено против движения). Следовательно, гружёный вагон дольше будет сохранять своё движение.

Итак, масса тела является мерой его инертности.

Из второго закона Ньютона следует,что любая сколь угодно малая сила может вызвать ускоренное движение тела.

Не противоречит ли этому то, что мы иногда, толкая тяжёлый предмет, не можем сдвинуть его с места? Нисколько не противоречит. Дело в том, что между предметом и полом существует трение, и нам, чтобы привести его в движение,надо преодолеть это трение, а для этого сила, с которой мы толкаем предмет, должна быть больше силы трения, что не всегда бывает.

Изменение скорости тела зависит от массы тела и от времени действия силы на тело. Это видно хорошо на следующем опыте.

Положим на одну чашку весов тяжёлую плиту и уравновесим её гирями или каким-нибудь другим грузом. Если резко ударить небольшим молоточком по плите, то равновесие весов не нарушится.

Если же положить на чашки весов тела с малой массой, то уже при самом незначительном ударе равновесие весов нарушится.

Чем больше масса тела, тем меньшее изменение скорости вызывает действующая на него сила. Это учитывается в технике.

Рис. 101. Машина на массивном фундаменте.

Так, например, для уменьшения сотрясений от ударов делают массивными и прочно соединяют с землёй мостовые „быки“ и упоры; массивными делают наковальни: относительные размеры молота и наковальни видны на рисунке 100. По этой же причине станки и машины делают массивными и устанавливают их на массивные фундаменты. На рисунке 101 изображена машина, установленная на массивном основании.

Нам известен способ определения массы тела с помощью взвешивания тела на рычажных весах. Второй закон Ньютона даёт нам другой способ определения массы — как меры инертности тела по величине силы и ускорению:

Опытом проверено, что оба эти способа определения массы тела (по весу и по инертности) дают совершенно одинаковые результаты.

Система единиц измерения механических величин

Чтобы применять формулы для числовых расчётов, необходимо установить, в каких единицах измеряются физические величины.

Физические законы связывают физические величины определёнными зависимостями. Поэтому если произвольно выбрать единицы для измерения некоторых величин, то единицы для измерения других величин получатся на основе соответствующих законов. Например, в формуле s = vt дана зависимость между тремя величинами. Если мы произвольно выберем единицы каких-нибудь двух величин, то единица третьей величины определится из этого уравнения. Условившись, например, измерять путь в метрах, а время в секундах, мы должны будем измерять скорость в

Зависимости, существующие между физическими величинами, дают возможность составить такую совокупность единиц, в которой для измерения механических величин достаточно выбрать произвольно три единицы: единицу длины, единицу массы, или силы, и единицу времени; такая совокупность единиц называется системой единиц.

Выбранные произвольно единицы системы называются основными единицами, а все другие — производными единицами.

В физике принята система единиц, в которой основными единицами являются: единица длины—1 см (сотая часть международного метра), единица массы— 1 г (тысячная часть международного килограмма) и единица времени—1 сек ( средних солнечных суток, измеряемая весьма точными часами, которые систематически проверяются астрономическими наблюдениями) (Солнечные сутки—промежуток времени между двумя следующими друг за другом полуднями. Так как продолжительность солнечных суток в разные времена года несколько различна, то в практику введены средние солнечные сутки, продолжительность которых равна средней длительности суток за год).

Эта система называется системой единиц CGS (по первым буквам слов—сантиметр, грамм, секунда).

Единица скорости в этой системе единица ускорения

Полагая в формуле F=ma второго закона Ньютона m = 1 г, получим единицу силы в системе CGS:

За единицу силы в системе CGS принимается такая сила, под действием которой масса в 1 г движется с ускорением, равным Эта единица называется диной (сокращённо дн).

В системе единиц, применяемой в настоящее время в СССР при электрических и магнитных измерениях, за основные единицы принимаются:

единица длины — 1 м,

единица массы — 1 кг,

единица времени — 1 сек,

единица тока — 1 ампер.

Сокращённо мы эту систему единиц будем называть MKSA (по первым буквам слов—метр, килограмм, секунда, ампер).

Единицей силы в системе MKSA будет такая сила, под действием которой масса в 1 кг движется с ускорением Эта единица называется ньютон (сокращённо н). Таким образом,

Вычислим, сколько в одном ньютоне содержится дин. или
В практике довольно широко распространена так называемая техническая система единиц. В этой системе основными единицами являются:

единица длины —1 м,

единица силы —1 кГ,

единица времени—1 сек.

Единица массы в этой системе единиц является производной и может быть определена из равенства т. е. единицей массы в технической системе единиц является масса, которая под действием силы в 1 кГ движется с ускорением

Сокращённое обозначение этой единицы—т. е. м. Таким образом,

Между различными единицами массы и силы существуют следующие соотношения:

1 кГ есть сила, с которой Земля притягивает массу в 1 кг и сообщает ей ускорение Отсюда: или округлённо:

Так как то 1 кГ = 9,8 н.

Примеры решения задач на второй закон Ньютона

1. Постоянная сила, равная 2 кГ, действует на тело, вес которого 19,6 кГ. С какой скоростью будет двигаться тело в горизонтальном направлении по прошествии 5 сек., если начальная скорость движения равна нулю?

Расчёты ведём в системе CGS.

Дано: F = 2 кГ=2*980000 дн = 1960000 дн;

m=19600 г; t = 5 сек. Найти

Под действием постоянной силы тело будет двигаться равноускоренно. Скорость этого тела определим по формуле:

Время t дано по условиям задачи.

Ускорение найдем на основании второго закона:

Ответ:
2. Тело весом 98 кГ движется со скоростью, равной
Какую силу надо приложить, чтобы остановить это тело в течение 5 мин.? Расчёты провести в технической системе единиц.

Дано: Р = 98 кГ; t = 300 сек. Найти F.

Искомую силу найдём на основании второго закона:

F = mа.

Под действием этой силы тело будет двигаться равнозамедленно, отрицательное ускорение его а определим по формуле;

Так как то

По второму закону Ньютона Р = mg, откуда

Ответ.

3. На тело, движущееся с начальной скоростью в подействовали силой в 10 Г в направлении движения, после чего тело прошло за 5 сек. путь в 200 м. Определить вес тела. Расчёты провести в системе CGS.

Вес тела в системе CGS, выражаемый в динах, найдётся на основании второго закона Ньютона:

Надо найти массу в граммах. Для этого воспользуемся тем F же вторым законом, ускорение а по условиям задачи вычислим по формуле:

откуда

Масса тела

Ответ.

При решении физических задач мы производим математические действия не только с числовыми значениями величин, но и над их наименованиями. Если предварительно все величины, указанные в задаче, выразить в единицах одной системы единиц и правильно применить соотношения, существующие между физическими величинами, то ответ всегда получится в единицах этой системы. Это позволяет нам не загромождать вычисления наименованиями единиц; достаточно указать наименование величины только в окончательном результате.

Пример. Тело массой 0,01 кг, двигаясь равноускоренно без начальной скорости, за 1 мин. прошло в горизонтальном направлении путь, равный 18 м. Определить силу, действующую на тело.

Дано: m = 0,01 кг; t = 1 мин.; s = 18 м. Найти F.

Выражаем все данные в задаче величины в единицах одной системы, например в системе CGS.

m = 10 г; t = 60 сек.; s = 1800 см.

По второму закону Ньютона F = ma. (1)

Масса дана, ускорение а находим по формуле пути равноускоренного движения: откуда

Подставим значение а из равенства (2) в равенство (1), получим:

Подставляя численные значения величин в равенство (3), определим величину силы F:

Услуги по физике:

Заказать физику
Заказать контрольную работу по физике
Помощь по физике

Лекции по физике:

Физические величины и их измерение
Основные законы механики
Прямолинейное равномерное движение
Прямолинейное равнопеременное движение
Сила
Взаимодействия тел
Механическая энергия
Импульс
Вращение твердого тела
Криволинейное движение тел
Колебания
Колебания и волны
Механические колебания и волны
Бегущая волна
Стоячие волны
Акустика
Звук
Звук и ультразвук
Движение жидкости и газа
Молекулярно-кинетическая теория
Молекулярно-кинетическая теория строения вещества
Молекулярно — кинетическая теория газообразного состояния вещества
Теплота и работа
Температура и теплота
Термодинамические процессы
Идеальный газ
Уравнение состояния идеального газа
Изменение внутренней энергии
Переход вещества из жидкого состояния в газообразное и обратно
Кипение, свойства паров, критическое состояние вещества
Водяной пар в атмосфере
Плавление и кристаллизация
Тепловое расширение тел
Энтропия
Процессы перехода из одного агрегатного состояния в другое
Тепловое расширение твердых и жидких тел
Свойства газов
Свойства жидкостей
Свойства твёрдых тел
Изменение агрегатного состояния вещества
Тепловые двигатели
Электрическое поле
Постоянный ток
Переменный ток
Магнитное поле
Электромагнитное поле
Электромагнитное излучение
Электрический заряд (Закон Кулона)
Электрический ток в металлах
Электрический ток в электролитах
Электрический ток в газах и в вакууме
Электрический ток в полупроводниках
Электромагнитная индукция
Работа, мощность и тепловое действие электрического тока
Термоэлектрические явления
Распространение электромагнитных волн
Интерференционные явления
Рассеяние
Дифракция рентгеновских лучей на кристалле
Двойное лучепреломление
Магнитное поле и электромагнитная индукция
Электромагнитные колебания и волны
Природа света
Распространение света
Отражение и преломление света
Оптические приборы и зрение
Волновые свойства света
Действия света
Линзы и получение изображений с помощью линз
Оптические приборы и глаз
Фотометрия
Излучение и спектры
Квантовые свойства излучения
Специальная теория относительности в физике
Теория относительности
Квантовая теория и природа поля
Строение и свойства вещества
Физика атомного ядра
Строение атома

Источник

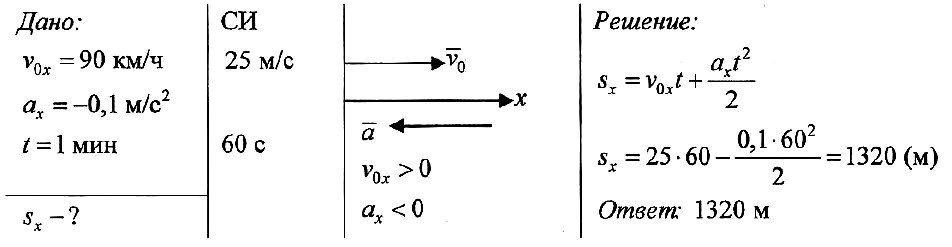
ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

Формулы, используемые в 9-11 классах по теме
«ЗАДАЧИ на Прямолинейное равноускоренное движение».

Название величины	Обозначение	Единица измерения	Формула
*Время*	t	с
*Проекция начальной скорости*	v_0x	м/с
*Проекция мгновенной скорости*	v_x	м/с
*Проекция ускорения*	a_x	м/с²
*Проекция перемещения*	S_x	м
*Координата*	x	м

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

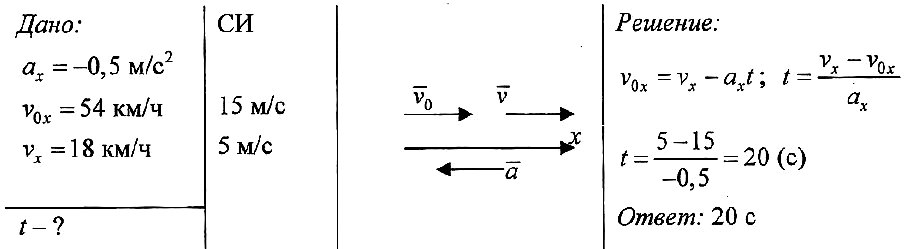
Задача № 1.
Автомобиль, двигаясь с ускорением –0,5 м/с², уменьшил свою скорость от 54 до 18 км/ч. Сколько времени ему для этого понадобилось?

Задача № 2.
При подходе к станции поезд начал торможение с ускорением 0,1 м/с², имея начальную скорость 90 км/ч. Определите тормозной путь поезда, если торможение длилось 1 мин.

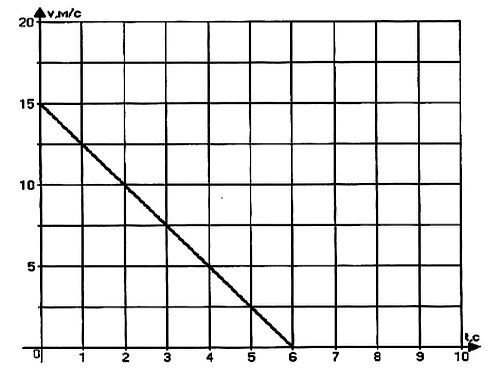
Задача № 3.
По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

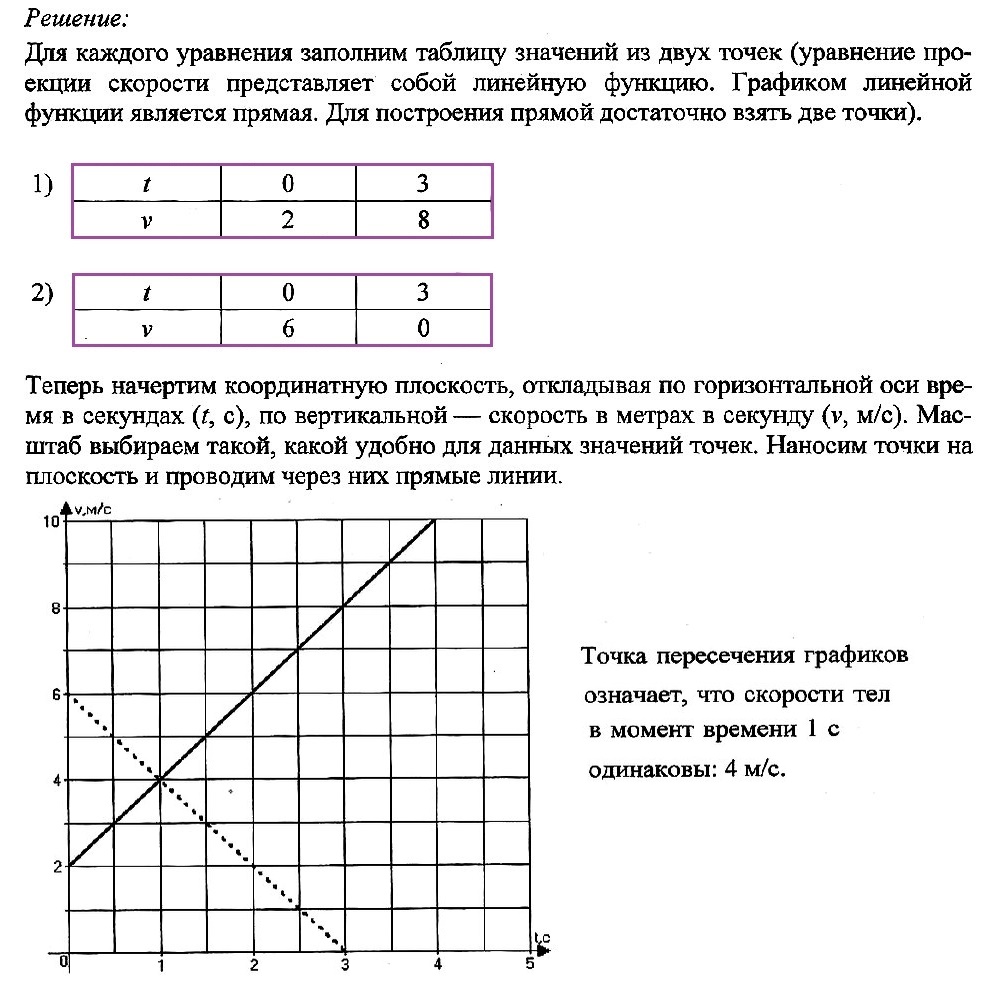
Задача № 4.
Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v₂_x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Задача № 5.
Движение тела задано уравнением x(t) = 5 + 10t — 0,5t². Определите: 1) начальную координату тела; 2) проекцию скорости тела; 3) проекцию ускорения; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) определите значение координаты и скорости в момент времени t = 4 с. Сравним уравнение координаты в общем виде с данным уравнением и найдем искомые величины.

Решение:

Задача № 6.
Вагон движется равноускоренно с ускорением -0,5 м/с². Начальная скорость вагона равна 54 км/ч. Через сколько времени вагон остановится? Постройте график зависимости скорости от времени.

Задача № 7.
Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с² в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Задача № 8.
Трамвай двигался равномерно прямолинейно со скоростью 6 м/с, а в процессе торможения — равноускоренно с ускорением 0,6 м/с². Определите время торможения и тормозной путь трамвая. Постройте графики скорости v(t) и ускорения a(t).

Задача № 9.
Тело, имея некоторую начальную скорость, движется равноускоренно. За время t = 2 с тело прошло путь S = 18 м, причём его скорость увеличилась в 5 раз. Найти ускорение и начальную скорость тела.

Задача № 10. (повышенной сложности)
Прямолинейное движение описывается формулой х = –4 + 2t – t². Опишите движение, постройте для него графики v_x(t), s_x(t), l(t).

Задача № 11.
ОГЭ
Поезд, идущий со скоростью v₀ = 36 км/ч, начинает двигаться равноускоренно и проходит путь S = 600 м, имея в конце этого участка скорость v = 45 км/ч. Определить ускорение поезда а и время t его ускоренного движения.

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

Перейти к теме: ЗАДАЧИ на Свободное падение тел с решениями
Посмотреть конспект по теме КИНЕМАТИКА: вся теория для ОГЭ (шпаргалка)
Вернуться к списку конспектов по Физике.
Проверить свои знания по Физике (онлайн-тесты).

Источник

Равноускоренное движение.

Зависимость скорости от времени.
Закон движения.
Прямолинейное равноускоренное движение.
Свободное падение.
Горизонтальный бросок.
Бросок под углом к горизонту.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение — это движение с постоянным вектором ускорения vec a . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

к оглавлению ▴

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

$frac{displaystyle dvec{v}}{displaystyle dt}=vec{a}$ . (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор vec a ? Разумеется, функцию vec a t . Но не только: к ней можно добавить ещё произвольный постоянный вектор vec c (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы vec c ? В начальный момент времени t=0 скорость равна своему начальному значению: $vec v=vec v_{0}$ . Поэтому, полагая t=0 в формуле (2), получим:

$vec v_{0}=vec c$ .

Итак, константа vec c — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

$vec v=vec v_{0}+vec {a}t$ . (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

$v_{displaystyle x}=v{displaystyle 0x}+a_{displaystyle x}t$ , (4)

$v_{displaystyle y}=v{displaystyle 0y}+a_{displaystyle y}t$ . (5)

Формула для третьей компоненты скорости, $v_{displaystyle z}$ если она необходима, выглядит аналогично.)

к оглавлению ▴

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

$frac{displaystyle dvec{r}}{displaystyle dt}=vec{v}$

Подставляем сюда выражение для скорости, даваемое формулой (3):

$frac{displaystyle dvec{r}}{displaystyle dt}=vec v_{0}+vec {a}t$ (6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить $vec v_{0}$ , надо продифференцировать функцию $vec v_{0}t$ . Чтобы получить , нужно продифференцировать $vec {a} t^{2} /2$ . Не забудем добавить и произвольную константу vec c :

$vec r=vec c+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

Ясно, что vec c — это начальное значение $vec r_{0}$ радиус-вектора vec r в момент времени t=0 . В результате получаем искомый закон равноускоренного движения:

$vec r=vec r_{0}+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ . (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ . (8)

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ . (9)

$z=z_{0}+ v_{displaystyle 0z} t+frac{displaystyle a_{displaystyle z} t^{2}}{displaystyle 2}$ . (10)

Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что $vec r - vec r_{0}=vec s$ — перемещение тела. Тогда
получаем зависимость перемещения от времени:

$vec s= vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

к оглавлению ▴

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

$v_{displaystyle x}=v_{displaystyle 0x}+a_{displaystyle x}t$ ,

$x=x_{0}+ v_{0 displaystyle x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$s_{x}= v_{0x} t+frac{displaystyle a_{x} t^{2}}{displaystyle 2}$ ,

где $s_{x}= x-x_{0}$ — проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

$t=frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}$

и подставим в формулу для перемещения:

$s_{x}= v_{0x} frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}+frac{displaystyle a_{x}}{2} (frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}})^{2}$ .

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

$s_{x}=frac{displaystyle v_{displaystyle x}^{displaystyle 2}-displaystyle v_{displaystyle 0x}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}$ .

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

к оглавлению ▴

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения vec g , направленным вертикально вниз. Почти во всех задачах при расчётах полагают g=10 м/с $^{2}$ .

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи h=2 км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

$s_{y}=frac{displaystyle v_{displaystyle y}^{displaystyle 2}-displaystyle v_{displaystyle 0y}^{displaystyle 2}}{displaystyle 2a_{displaystyle y}}$ .

Имеем: $s_{y}=h, v_{y}=v$ — искомая скорость приземления, $v_{0y}=0, a_{y}=g$ . Получаем: $h^{2}=frac{v^{2}}{2g}$ , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью $v_{0}=30$ м/с. Найти его скорость через t=5 c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$v_{displaystyle y}=v_{displaystyle 0y}+a_{displaystyle y}t$ .

Здесь $v_{displaystyle 0y}=v_{0}, a_{y}=-g$ , так что $v_{displaystyle y}=v_{displaystyle 0}-gt$ . Вычисляем: $v_{displaystyle y}=30-10 cdot 5=-20$ м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте h=15 м, бросили вертикально вверх камень со скоростью $v_{0}=10$ м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

Имеем: $y=0, y_{0} = h, v_{0y}=v_{0}, a_{y}=-g,$ так что $0=h+v_{0}t-frac{displaystyle g t^{2}}{displaystyle 2}=15+10t-5t^{2}$ , или $t^{2}-2t-3=0$ . Решая квадратное уравнение, получим t=3 c.

к оглавлению ▴

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью $v_{0}$ с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат OXY так, как показано на рис. 1.

Рис. 1. Горизонтальный бросок

Используем формулы:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$

В нашем случае $x_{0} = 0, v_{0x}=v_{0}, a_{x}=0, y_{0} = h, v_{0y}=0, a_{y}=-g$ . Получаем:

$x=v_{0}t, y=h-frac{displaystyle g t^{2}}{displaystyle 2}$ . (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

$y(T)=0Rightarrow h-frac{displaystyle gT^{displaystyle 2}}{displaystyle 2}=0Rightarrow T=sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Дальность полёта — это значение координаты в момент времени :

$L=x(T)=v_{0}T=v_{0} sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

$t=frac{displaystyle x}{displaystyle v_{displaystyle 0}}Rightarrow y=h-frac{displaystyle g}{displaystyle 2}(frac{displaystyle x}{displaystyle v_{displaystyle 0}})^{displaystyle 2}=displaystyle h-frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{displaystyle 0}}$ .

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

к оглавлению ▴

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью $v_{0}$ , направленной под углом alpha к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат OXY так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

В нашем случае $x_{0} =y_{0}=0, v_{0x}=v_{0}cos alpha, v_{0y}=v_{0}sin alpha , a_{x}=0, a_{y}=-g$ . Получаем:

$x=(v_{0}cos alpha )t, y=(v_{0}sin alpha)t- frac{displaystyle g t^{2}}{displaystyle 2}$ .

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

$T=frac{displaystyle 2v_{displaystyle 0}sinalpha }{displaystyle g}$ ,

$L=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin2alpha }{displaystyle g}$ ,

$y=x tgalpha -frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{0}cos^{displaystyle 2}alpha }$ .

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

$H=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin^{2} alpha }{displaystyle 2g}$ .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Равноускоренное движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Кинематика — это специальный раздел теоретической механики. Направление сформировалось несколько позднее, чем статика и динамика: во второй половине XIX столетия. Первые исследования в области кинематики были посвящены огнестрельному оружию. Ученые стремились понять процесс полета снаряда, производили расчет траектории его движения. В дальнейшем кинематика как научное направление получило широкое распространение и существенно повлияло на развитие технического прогресса.

Кинематика — описание

Кинематика является разделом механики, цель которого — изучение механического движения тел с пренебрежением к причинам, вызывающим это движение.

Механика представляет собой научную область физики, которой посвящены исследования механического движения тел. Основной целью данного направления служит определение точного положения тела в пространстве в любой момент времени. Важным понятием этого раздела является материальная точка в виде тела с определенной массой и размерами, которыми можно пренебречь для решения задачи при наличии следующих условий:

Путь, который преодолевает тело, существенно больше, чем его размеры.
Расстояние между телами значительно превышает их размеры.
Объект совершает поступательное движение.

Движение тела рассматривают в системе отсчета, состоящей из системы координат и прибора, измеряющего время. Траекторией называют линию, которую объект описывает, совершая движение. Путь является скалярной величиной, определяемой как длина траектории. Перемещением обозначают вектор, который соединяет начальное и конечное положение тела, преодолеваемое им в течение определенного промежутка времени.

Совершая движение, тело может только увеличивать пройденный путь, при этом перемещение увеличивается или уменьшается. К примеру, уменьшение перемещения наблюдается во время обратного движения тела. Если объект движется прямолинейно в одном направлении, то путь определяется модулем перемещения. В случае криволинейного движения — путь превышает перемещение. При рассмотрении замкнутой траектории перемещение будет равно нулю.

Теория и формулы

Благодаря многолетним исследованиям в области кинематики ученым удалось вывести определенные закономерности движения тела. С помощью справедливых уравнений представляется возможным ответить на многие вопросы о разных характеристиках, которые изменяются либо остаются постоянными во время движения объектов.

Путь, время, скорость

Расстояние представляет собой удаленность одной точки положения тела от другой. Тело преодолевает путь, который представляет собой важную характеристику механического движения. Общепринятым обозначением пути является латинская буква s. Данный параметр измеряют метрами и километрами, если речь идет о больших расстояниях.

Скорость представляет собой путь, который тело преодолело в течение единицы времени. В качестве единицы времени часто используют 1 час, 1 минуту, 1 секунду. Для расчета скорости необходимо определить отношение пути к времени движения. В случае, когда в условиях задачи расстояние измеряется в метрах, а время пути — в секундах, то скорость следует рассчитывать в метрах в секунду (м/с). Для обозначения скорости используют латинскую букву (v).

Нередко требуется определить время пути. Данный параметр обозначают с помощью латинской буквы (t).

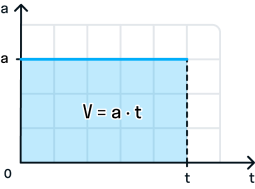
Важно отметить, что скорость, путь и время взаимосвязаны. При известных характеристиках скорости и времени можно определить расстояние, которое преодолело тело. Путь в данном случае равен произведению скорости и времени, рассчитывается по формуле:

(s=vtimes t)

При известных величинах времени и расстояния достаточно просто определить скорость движения тела, руководствуясь следующим уравнением:

(v=frac{s}{t})

Равномерное движение

Равномерным движением называют движение тела, которое совершает равные перемещения в течение любых равных промежутков времени.

Мячи

Источник: goodfon.ru

Скорость при равномерном движении определяется как отношение перемещения ко времени, в течение которого данное перемещение было совершено. Уравнение имеет следующий вид:

(vec{v}=frac{vec{s}}{t})

(vec{v}=const)

Проекция вектора скорости на ось ОХ выглядит таким образом:

(v_{x}=frac{s_{x}}{t})

(v_{x}=const)

Если вектор скорости спроецировать на ось координат, то она будет равна быстроте изменения данной координаты:

(v_{x}=frac{x-x_{0}}{t})

Прямолинейное равноускоренное движение

Прямолинейным равноускоренным движением называют движение по прямой траектории, для которого характерно постоянное ускорение.

Ускорение для прямолинейного равноускоренного движения обозначают следующим образом:

(vec{a}=const)

При таком движении можно наблюдать увеличение или уменьшение скорости. Чтобы определить скорость, необходимо выполнить следующий расчет:

(vec{v}=vec{v}_{0}+vec{a}t)

Если тело разгоняется в проекции оси ОХ, то скорость можно определить по формуле:

(v_{x}=v_{0x}+a_{x}t)

a>0, движение является равноускоренным.

Направление 1

Источник: fizi4ka.ru

Во время торможения в проекции на ось ОХ скорость рассчитывают следующим образом:

(v_{x}=v_{0x}-a_{x}t)

а<0, движение является равнозамедленным.

Направление 2

Источник: fizi4ka.ru

Графически зависимость ускорения от времени, то есть график ускорения во время равноускоренного движения тела, можно представить в виде:

Зависимость

Источник: fizi4ka.ru

График ускорения, характеризующий равноускоренное движение тела, представляет собой прямую, которая параллельна оси времени:

график 1 находится над осью t, тело совершает разгон, ах>0;
график 2 размещен под осью t, тело тормозит, ах<0.

Графически скорость или проекция скорости изображается в виде зависимости скорости от времени:

Графически скорость

Источник: fizi4ka.ru

Графически скорость, характерная для равноускоренного движения тела, имеет вид прямой. График 1 направлен вверх, тело будет совершать равноускоренное движение в положительном направлении оси ОХ:

(v_{0x}>0)

(a_x>0)

(a_{1x} = tg α )

График 2 направлен вниз, тело будет двигаться равнозамедленно в положительном направлении оси ОХ:

(v_{0x}>0)

(a_x<0)

(a_{2x} = tg α )

График 3 направлен вниз, тело свершает равноускоренное движение против оси ОХ:

(v_{0x}<0)

(a_x<0)

Исходя из графика зависимости скорости от времени, определяют перемещение, которое тело преодолело в течение определенного промежутка времени (t_2-t_1). В этом случае целесообразно рассчитать площадь фигуры, расположенной под графиком. Формула для определения перемещения при равноускоренном движении имеет вид:

(S_{x}=v_{0x}t+frac{a_{x}t^{2}}{2})

(S_{x}=frac{v^{2}-v_{0}^{2}}{2a})

Перемещение в n-ую секунду во время равноускоренного движения можно определить по формуле:

(S_{n}=frac{a}{2}left(2n-1 right))

Определить координату тела, которое совершает равноускоренное движение, можно с помощью справедливого уравнения:

(x=x_{0}+v_{0x}t+frac{a_{x}t^{2}}{2})

Движение тела, брошенного вертикально вверх (вниз)

Во время падения тела вниз вектор его скорости направлен в ту же сторону, что и вектор ускорения свободного падения.

Баскетбол

Источник: goodfon.ru

Формулы, описывающее это движения, имеют следующий вид:

(vec{v} ↑↑vec{g})

(h=v_{0}t+frac{gt^{2}}{2})

(v=v_{0}+gt)

(h=frac{v^{2}-v_{0}^{2}}{2g})

В случае, когда тело падает вниз и его начальная скорость равна нулю, (v_0=0). Время падения при этом можно рассчитать по формуле:

(t=sqrt{frac{2h_{0}}{g}})

(h) является начальной высотой.

Для брошенного вверх тела будут справедливы следующие равенства:

(h=v_{0}t-frac{gt^{2}}{2})

(v=v_{0}-gt)

(h=frac{v^{2}-v_{0}^{2}}{-2g})

В максимальной верхней точке тело, брошенное вверх, будет обладать нулевой скоростью, (v=0). Для расчета времени подъема можно воспользоваться формулой:

(t=frac{v_{0}}{g})

Свободно падающее тело

Свободным падением называют движение тела в условиях безвоздушного пространства под действием силы тяжести.

В условиях свободного падения ускорения тел с разной массой будут равны. Данный параметр называют ускорением свободного падения. Оно всегда направлено к центру нашей планеты, то есть вертикально вниз. Величина обозначается латинской буквой g, а единицами измерения являются м/с².

Ускорение свободного падения равно 9,8 м/с². В задачах по физике допускается использовать значение g=10 м/с².

Движение по окружности с постоянной по модулю скоростью

Движением по окружности при постоянной по модулю скоростью называют простейшим видом криволинейного движения.

Траектория такого движения будет представлена в виде окружности. Вектор скорости тела приобретает направление по касательной к окружности. Модуль скорости тела при изменении времени остается постоянным, а направление движения в каждой точке изменяется. Из этого можно сделать вывод, что движение по окружности представляет собой движение с ускорением. В свою очередь ускорение, изменяющее направление скорости, носит название центростремительного.

Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростримительное ускорение

Источник: fizi4ka.ru

Центростремительное ускорение является характеристикой быстроты изменения направления вектора линейной скорости. Параметр обозначается, как ацс. Единицами измерения центростремительного ускорения служат м/с². Формула для расчета следующая:

(а_{цс} = frac{v^{2}}{R})

Движение тела по окружности при постоянной по модулю скорости называют периодическим движением. Таким образом, его координата будет повторяться через одинаковые периоды времени. Периодом называют время, в течение которого тело совершает один полный оборот. Обозначается величина как Т. Единицами измерения периода являются секунды, с. Для расчета справедливо равенство:

(T=frac{t}{N})

(N) является количеством оборотов, (t) — временем, за которое тело совершает обороты.

Частота вращения представляет собой количество оборотов за единицу времени. Обозначается параметр в виде латинской буквы (ν). Единицами измерения являются (с^{-1}) (Гц).

(nu=frac{N}{t})

Период и частота являются взаимно обратными величинами:

(T=frac{1}{nu})

(nu =frac{1}{T})

Линейная скорость представляет собой скорость движения тела по окружности. Параметр обозначают латинской буквой v, единицами измерения являются м/с. Линейная скорость направлена по касательной к окружности и рассчитывается по формуле:

(v=frac{2pi times R}{T})

(R) является радиусом окружности.

Угловой скоростью называют физическую величину, которая определяется как отношение угла поворота и времени, за которое тело совершает этот поворот. Обозначают параметр как ω. Единицами измерения угловой скорости являются рад/с. Угловая скорость определяется по формуле:

(omega =frac{varphi }{t})

(varphi) представляет собой угол поворота.

Угловая скорость

Источник: fizi4ka.ru

Направление угловой скорости определяют с помощью правила правого винта или буравчика. В случае, когда вращательное движение винта соотносится с направлением движения тела по окружности, то поступательное движение винта и направление угловой скорости совпадают. Связь параметров движения тела по окружности представлена следующими формулами:

(v=omega R)

(omega =frac{v}{R})

(a_{сц} = omega ^{2}R)

(omega = frac{2pi }{T})

(omega = 2pi v)

Во время равномерного движения тела по окружности точки, расположенные на радиусе, перемещаются с равной угловой скоростью, так как радиус за одно и то же время поворачивается на одинаковый угол. В это время линейная скорость разных точек радиуса отличается в зависимости от того, насколько близко или далеко от центра они размещены:

(v_{1}=omega r)

(v_{2}=omega R)

(frac{v_{1}}{v_{2}}=frac{r}{R})

Угловая скорость 2

Источник: fizi4ka.ru

При рассмотрении равномерного движения двух соединенных тел можно наблюдать отсутствие отличий в линейных скоростях, но при этом угловые скорости тел будут различны в зависимости от радиуса тела:

(omega _{1}=frac{v}{R_{1}})

(omega _{2}=frac{v}{R_{2}})

(frac{omega _{1}}{omega _{2}}=frac{R_{1}}{R_{2}})

Окружности

Источник: fizi4ka.ru

Движение тела, брошенного под углом к горизонту

Движение тела, которое бросили под углом к горизонту, можно представить в виде суперпозиции двух движений:

Равномерного горизонтального перемещения.
Равноускоренного движения вертикально при ускорении свободного падения.

Движение тела

Источник: fizi4ka.ru

Формула скорости будет иметь следующий вид:

(v_{0x}=v_{x}=v_{0} cos alpha =const)

(v_{0y}=v_{0}sin alpha)

(v_{y}=v_{0}sin alpha-gt)

Уравнение координаты обладает следующим видом:

(x=v_{0}cos alpha times t)

(y=v_{0}sin alpha times t-frac{gt^{2}}{2})

Скорость тела в любое время будет равна:

(v=sqrt{v_{x}^{2}+v_{y}^{2}})

Найти угол между вектором скорости и осью ОХ можно по формуле:

(tan beta =frac{v_{y}}{v_{x}}=frac{v_{0}sin alpha -gt}{v_{0}cos alpha })

Время подъема на максимальную высоту равно:

(t=frac{v_{0}sin alpha }{g})

Максимальную высоту подъема можно рассчитать с помощью формулы:

(h_{max}=frac{v_{0}^{2}sin ^{2}alpha}{2g})

Время полета соответствует уравнению:

(t=frac{2v_{0}sin alpha }{g})

Максимальную дальность полета можно рассчитать по формуле:

(L_{max}=frac{v_{0}^{2}sin 2alpha }{g})

Движение тела, брошенного горизонтально

Движение тела, которое бросили горизонтально, представлено в виде суперпозиции двух движений:

Равномерное горизонтальное движение со скоростью v0=v0x.
Равноускоренное вертикальное движение при ускорении свободного падения g с нулевой начальной скоростью.

Движение тела 2

Источник: fizi4ka.ru

Уравнение скорости:

(v_{x}=v_{0x}=const)

(v_{y}=g_{y}t=-gt)

Мяч

Источник: implus.com

Уравнение координаты:

(x=v_{0x}t=v_{x}t)

(y=frac{g_{y}t^{2}}{2}=h_{0}-frac{gt^{2}}{2})

Скорость тела в любое время будет определяться по формуле:

(v=sqrt{v_{x}^{2}+v_{y}^{2}})

Дальность полета тела соответствует уравнению:

(l=v_{0x}t=v_{0x}sqrt{frac{2h_{0}}{g}})

Вычислить угол между вектором скорости и осью ОХ можно с помощью формулы:

(tan beta =frac{v_{y}}{v_{x}}=frac{-gt}{v_{0x}})

Задачи по кинематике, их решение

Задача 1

Рассмотрим путь велосипедиста из одного населенного пункта в другой. Половина расстояния была преодолена со скоростью 12 км/ч ((v_1)). Далее половину оставшегося времени он ехал со скоростью 6 км/ч ((v_2)). Остаток расстояния путник преодолел пешком со скоростью 4км/ч ((v_3)). Необходимо рассчитать среднюю скорость на всем пути следования велосипедиста.

Решение

Данный пример относится к теме равномерного прямолинейного движения одного тела. Процесс можно изобразить схематично:

Решение

Источник: pandia.ru

(S = S_1 + S_2 + S_3)

(t = t_1 + t_2 + t_3)

На каждый отрезок пути необходимо составить уравнение движения:

(S_1 = v_1t_1)

(S_2 = v_2t_2)

(S_3 = v_3t_3)

Далее можно представить дополнительные условия задачи:

(S_1 = S_2 + S_3)

(t_2 = t_3)

(v_{sr}=frac{S}{t}=frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}})

Следует преобразить формулу и подставить числовые значения:

(v_{sr}=frac{2S_{1}}{frac{S_{1}}{v_{1}}+frac{2S_{1}}{v_{2}+v_{3}}}=frac{2v_{1}left(v_{2}+v_{3} right)}{2v_{1}+v_{2}+v_{3}})

(v_{sr}=frac{2times 12left(6+4 right)}{2times 12+6+4}=7)

Ответ: средняя скорость составляет (7) км/ч.

Задача 2

Тело подбросили вертикально вверх. Начальная скорость при этом составила 3,13 м/с ((v_0)). В момент, когда данное тело достигло максимальную высоту полета, из начального пункта подбросили второе тело с такой же начальной скоростью, как у первого. Необходимо определить на каком расстоянии от точки бросания встретятся тела. Сопротивлением воздуха при решении можно не учитывать.

Решение

Схематично перемещение тел можно представить следующим образом:

Задача 2

Источник: pandia.ru

Формула, описывающая движение тела, которое подбросили вверх, необходима для вычисления координаты движущегося тела в любое время. Для первого тела справедливо уравнение:

(h=v_{0}t_{1}-frac{gt_{1}^{2}}{2})

Для второго тела можно представить следующую формулу:

(h=v_{0}t_{2}-frac{gt_{2}^{2}}{2})

Следующую формулу можно составить на основании условия задачи, в котором указано, что второе тело бросили позднее первого на время максимального подъема:

(t_{1}-t_{2}=frac{v_{0}}{g})

Объединяя уравнения в систему из трех формул относительно величины (h) получим:

(h=frac{3}{4}frac{v_{0}^{2}}{2g})

(h=frac{3}{4}frac{3.13^{2}}{2*9.8}=0.37)

Ответ: тела встретятся на высоте (0,37) м.

Задача 3

Камень, находясь в свободном падении, вторую часть пути преодолел за 1 секунду. Необходимо вычислить высоту (h), с которой упал камень.

Решение

Ось Y системы координат, в которых падает камень, направлена вертикально вниз. В качестве начала координат можно принять точку, из которой камень упал. Закон перемещения данного тела в проекции на ось будет обладать следующим видом:

(h=v_{0}t+frac{gt^{2}}{2})

(h=frac{gt^{2}}{2})

(v=v_{0}t+gt)

(v=gt)

Время падения камня рассчитывается по формуле:

(t=sqrt{frac{2h}{g}})

Для середины пути, который преодолел камень, справедливы уравнения:

(frac{h}{2}=frac{gt_{1}^{2}}{2})

(t_{1}=sqrt{frac{h}{g}})

Время (t_2), которое потребовалось телу на преодоление второй половины пути, указанное в условии задачи, рассчитывается по формуле:

(t_{2}=t-t_{1}=sqrt{frac{2h}{g}}-sqrt{frac{h}{g}})

(t_{2}^{2}=frac{h}{g}left(sqrt{2} -1right)^{2})

Исходя из данного уравнения, можно вычислить высоту:

(t_{2}^{2}=frac{h}{g}left(sqrt{2} -1right)^{2})

(h=frac{t_{2}^{2}g}{left(sqrt{2}-1 right)^{2}}=frac{9,81}{0,17}=57,7)

Ответ: камень упал с высоты (57,7) м.

Решение задач по кинематике основано на простых формулах. Успешность результата зависит от умения грамотно применять справедливые уравнения в том или ином случае. Бывают ситуации, когда в процессе изучения физики возникают некоторые трудности. Простым решением будет обратиться к порталу Феникс.Хелп.

Источник

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

Vк=Vн+at

Формула для ускорения при равноускоренном движении:

a=(Vк-Vн)/t

Задача 1

Формула расстояния при равноускоренном движении

S = t*(Vн+ Vк)/2

S = Vнt + at2/2 = t*(Vн + at/2)

2аS = Vк2−Vн2

Задача 2

Перемещение при равноускоренном движении

Равноускоренное движение: графически

Задача 3

Масса

Второй закон Ньютона

Масса — мера инертности тела

Система единиц измерения механических величин

Примеры решения задач на второй закон Ньютона

ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями

Название величины

Обозначение

Единица измерения

Формула

t

v0x

vx

ax

Sx

x

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Краткое пояснение для решения ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренное движение.

Зависимость скорости от времени.

Закон движения.

Прямолинейное равноускоренное движение.

Свободное падение.

Горизонтальный бросок.

Бросок под углом к горизонту.

Кинематика — описание

Теория и формулы

Путь, время, скорость

Равномерное движение

Прямолинейное равноускоренное движение

Движение тела, брошенного вертикально вверх (вниз)

Свободно падающее тело

Движение по окружности с постоянной по модулю скоростью

Движение тела, брошенного под углом к горизонту

Движение тела, брошенного горизонтально

Задачи по кинематике, их решение

Не пропустите также:

V_к=V_н+at

a=(V_к-V_н)/t

S = t*(V_н+ V_к)/2

S = V_нt + at²/2 **= t*(V_н + at/2)**

2аS = V_к²−V_н²

ЗАДАЧИ на Прямолинейное равноускоренное
движение с решениями

v_0x

v_x

a_x

S_x

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.